用于分割无损检测图像的快速模糊C均值算法

王军芬， 刘培跃， 董建彬， 朱占龙

(1.河北地质大学 信息工程学院，河北 石家庄 050031； 2.河北地质大学 智能传感物联网技术河北省工程研究中心，河北 石家庄 050031； 3.石家庄职业技术学院 机电工程系，河北 石家庄 050081)

0 引言

图像分割在许多领域都有着重要的应用，如机器视觉、医学影像、目标识别等[1-3]。模糊分割方法，尤其是模糊C均值(FCM)算法[4]及其变化在许多图像分割和目标分类应用中取得了良好的效果[5-11]。但是，对于不平衡数据，FCM的分割效果并不理想。到目前为止，仅有少数研究试图改善不平衡数据的聚类性能，例如有半监督的模糊C均值(ssFCM)算法[5]；对聚类尺寸不敏感的模糊C均值(cluster size insensitive FCM,CsiFCM)算法[12]，其实验结果表明CsiFCM的分割效果(或聚类性能)优于ssFCM；基于完整性的、对聚类尺寸不敏感的模糊C均值算法(size-insensitive integrity-based FCM，siibFCM)[13]，其聚类思想与CsiFCM大致相同，都是对较大的类群赋较小的条件值，较小的类群赋较大的条件值，不过siibFCM设计了更为复杂的条件值计算方法；多聚类中心的模糊C均值算法[14]在聚类过程中，设置类的个数大于实际值，这样多数类就会被拆分到少数类中，聚类之后再合并，从而改善聚类尺寸敏感问题。

当图像被噪声污染后，这些算法针对不平衡数据分割的鲁棒性较差，分割效果不理想。为了改善上述情况，本文提出一种快速鲁棒的，且对聚类尺寸不敏感的模糊C均值聚类图像分割算法。首先，利用局部空间算子和局部灰度算子对图像I0进行预处理得到非线性加权求和图像I，以提高算法的鲁棒性；其次，对非线性加权求和图像I的灰度级进行分类，在分类的过程中引入条件变量fg，将低条件值分配给较大类群的对象，并将高条件值分配给较小类群的对象来防止小类群向大类群漂移[12]，图像的分割时间不再取决于图像的大小，而是图像的灰度级数，从而大大降低算法的时间复杂度。

1 基于灰度级的模糊C均值算法

灰度图像的尺寸N=m×n，灰度级数为G，图像灰度级的集合I={I1,I2,…,IG},Ig表示第g个灰度级的值，把图像分割为C个区域，得到C个模糊子集，每一个模糊子集对应一个聚类中心vi，聚类中心集合V={v1,v2,…,vC}。目标函数为

(1)

(2)

(3)

式中：i=1,2,…,C;g=1,2,…,G。

利用式(2)和式(3)不断迭代更新直到满足设定的终止条件，得到各聚类中心和每个灰度级的隶属度值，根据式(4)将灰度级Ig分配给具有最高隶属度的k类：

k=argmaxμig,i=1,2,…,C。

(4)

对于不平衡数据，由于FCM使用了一个平方和形式的代价函数，使得小类群的中心倾向于向邻近的大类群漂移[12]，分割结果趋向于均衡聚类类群,分割效果不理想。

2 本文算法

原始灰度图像I0大小N=m×n，总像素集合X={x1,x2,…,xN}，灰度级数为G。本文中图像的预处理是指对原始图像I0按照式(5)进行预处理，形成一个非线性加权求和图像I：

(5)

式中：Ik∈[0,G-1]为非线性加权求和图像I的第k个像素的灰度值；Nk为以第k个像素为中心，大小为M×M的窗口邻域像素集合；xj为以第k个像素为中心的窗口中第j个像素的灰度值；Skj为第k个像素和第j个像素之间的局部相似性度量，表示第j个像素的权重，具体表述见文献[6]。

2.1 分割处理

非线性加权求和图像I中G≪N，将图像分割为C个区域，可得到C个模糊子集，每一个模糊子集对应一个聚类中心vi，聚类中心集合为V={v1,v2,…,vC}。目标函数定义为

(6)

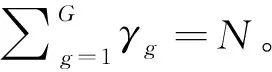
为了改善算法对不平衡数据的聚类性能，在聚类过程中，引入条件变量fg(0≤fg≤1)，将低条件值分配给较大类群的对象，并将高条件值分配给较小类群的对象来防止小类群向大类群漂移[12]。定义条件变量fg为

(7)

式中：Pimin为所有类群先验概率的最小值；fg为第g个灰度级去模糊后被分类为i类的条件值；Pi为第i类类群先验概率。

(8)

式中：Ni为属于类群i的所有灰度级g的像素总数。

Ni=∑gγg。

(9)

每个灰度级一旦被分配到某个特定的类群，就具有相对于所有类群的固定条件值，并且同一类群中的所有灰度级都具有相同的条件值。

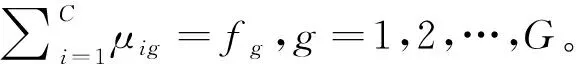
(10)

(11)

式中：i=1,2,…,C;g=1,2,…,G。

2.2 时间复杂度分析

本文算法的时间复杂度包括图像的预处理和分割处理。图像预处理主要是为了获得非线性加权求和图像I，其时间复杂度为O(nM2)；分割处理主要是算法的迭代过程，其时间复杂度为O(GC2Iter)，Iter为迭代次数。所以本文算法的时间复杂度为O(nM2+GC2Iter)。

2.3 具体步骤

步骤1 设置图像分割的区域数目C≥2、迭代终止条件ε>0、模糊指数m、最大的迭代次数Itermax；

步骤2 图像预处理，利用式(5)计算非线性加权求和图像I；

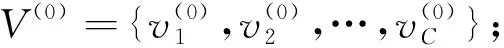
步骤4 初始化fg=1/C，g=1,2,…,G；

步骤5 用式(10)更新隶属度；

步骤6 根据隶属度按式(4)将每个灰度级g分配到适当的类群；

步骤7 用式(7)更新fg；

步骤8 用式(11)更新各个类的聚类中心V；

步骤9 重复步骤5～8直到满足终止条件：迭代次数Iter>Itermax或|V(Iter)-V(Iter-1)|<ε；

步骤10 根据最终的隶属度按式(4)对图像I中的每个灰度级进行去模糊。

3 实验与结果分析

3.1 实验参数设置及说明

实验图像由合成图像和无损检测图像构成,合成图像由4类图像数据组成，其中大类群与小类群的比值为29.16。选择无损检测图像Im1～Im6，其图像灰度分布具有不均衡性，目标类和背景类差异较大，所选图像满足对实验图像的要求。

首先,本文研究了条件变量fg随Ni的变化情况，其次，为了更好地验证算法优越性，用高斯噪声(均值为0，归一化方差为2%～8%)、椒盐噪声(噪声百分比为10%～15%)、瑞利噪声(均值为0，标准差为15～30)和乘性噪声(均值为0，方差为4%～8%)去污染实验图像，使用FCM、CsiFCM、siibFCM作为对比算法进行实验。设置模糊指数m=2，迭代精度ε=0.000 01，最大迭代次数为100。为了使分割结果不受初始类中心的影响，在相同噪声水平下进行对比实验时，选用相同的初始类中心。实验所用计算机的CPU为Intel CORE i7-8565U@1.80 GHz，RAM为8 GB，运行环境为Windows 7，编程环境为MATLAB R2014a。

针对不平衡数据聚类的图像分割结果，本文采用了3种评价标准：分割精度(SA)、F-value[15]、G-mean[16]。分割精度定义为分类正确的像素数与图像像素总数的比值；F-value用来评价聚类算法对少数类的聚类性能；G-mean用来评价聚类算法的总体性能。SA、F-value、G-mean值越大说明图像分割效果越好。当图像分割区域数为2时，选用评价标准F-value、G-mean；当图像分割区域数多于2时，选用SA。

3.2 条件变量fg随Ni的变化过程

合成图像像素为256×256=65 536，共由4类图像数据组成，如图1(a)所示。类1：灰度值为0的小正方形，1 600像素；类2：灰度值为80的水平线，8 640像素；类3：灰度值为160的垂直线，8 640像素；类4：灰度值为255的大正方形，46 656像素。

图1 合成图像及Ni、 fg测试结果Figure 1 Synthetic image and test results of Ni and fg

以被高斯噪声(均值为0，归一化方差为2%)污染后的图像为实验图像，如图1(b)所示，在图像的分割过程中条件变量fg随Ni的变化情况如图1(c)、1(d)所示。从图1(c)、1(d)中可以看出，当类群所包含的像素数目越大时，分配给所有属于类群的灰度级的条件值就越小；当类群i所包含的像素数目越小时，分配给所有属于类群的灰度级的条件值就越大。fg可以平衡不同大小的类群，解决类大小敏感问题。

3.3 合成图像分割实验

合成图像添加不同强度的噪声进行图像分割测试，结果如表1所示，其中NA表示失效。表1表明：从整体上看本文算法分割精度SA为97.93%，明显优于对比算法，甚至当对比算法失效时，本文算法仍能够得到较好效果。当图像没有噪声或被瑞利噪声污染时，本文算法与对比算法性能基本一致。但是当高斯噪声、椒盐噪声和乘性噪声归一化方差增大时，对比算法的分割精度都明显降低，而本文所提算法可以达到90%以上的分割精度，其主要原因是本文算法在聚类过程中引入了条件变量，提高了算法的分割精度。图2给出了当高斯噪声的归一化方差为2%时，各算法的分割效果。从图2中可以看出，本文算法对像素的不均性分布不敏感，分割效果受噪声影响较小，鲁棒性要优于对比算法。

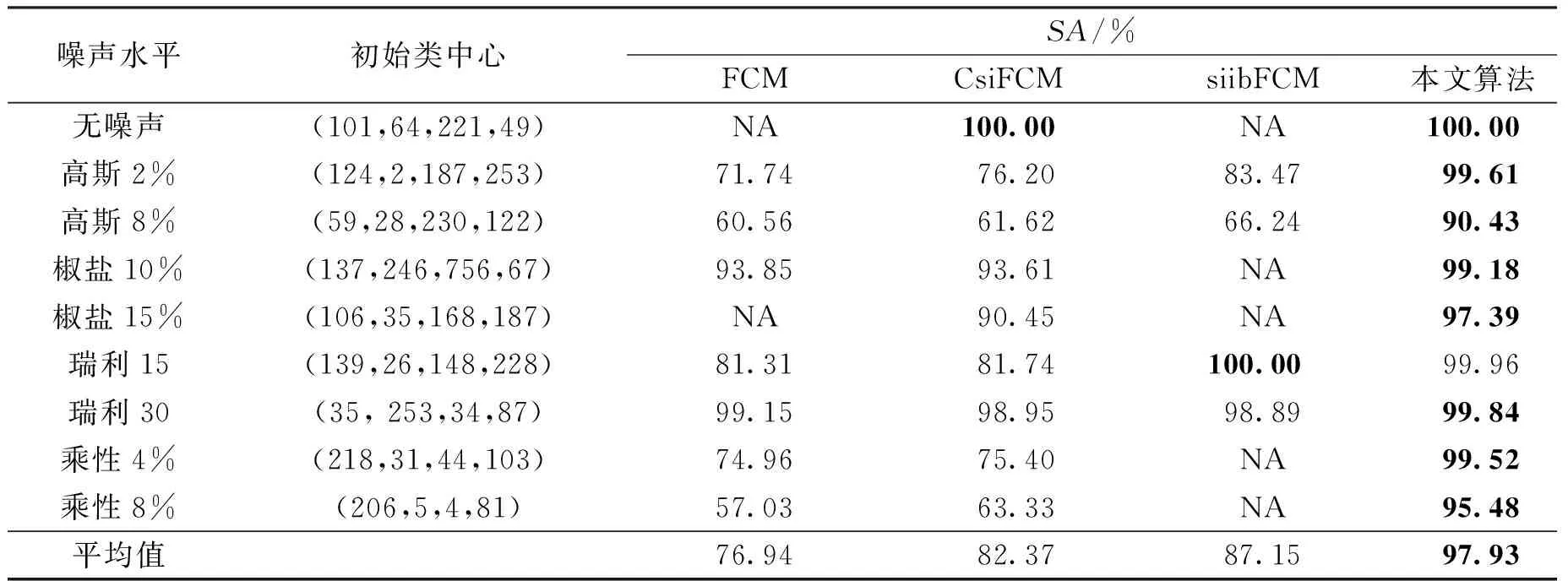
表1 不同噪声水平下的分割精度对比Table 1 Segmentation accuracy with different level noises

图2 高斯噪声2%时合成图像各算法分割结果Figure 2 Segmentation results on synthetic image corrupted by 2% Gaussian noise

3.4 无损检测图像分割实验

为了验证本文算法在无损检测图像分割方面的优越性，对尺寸不同、背景类与目标类大小比值不同，但差异较大的6幅无损检测图像进行图像分割，分为背景和目标物两类。无损检测图像Im1～Im6如图3所示，其图像像素依次为131×232、51×98、70×100、74×111、56×271、256×256，评价指标为F-value、G-mean以及分割图像所需要的时间(t)。本文算法与对比算法在不同噪声水平下各指标测试结果如表2、图4所示。其中的G-mean和t为图像在不同噪声水平下的平均值。

图3 无损检测图像Figure 3 Non-destructive testing images

当图像被高斯噪声、椒盐噪声、瑞利噪声以及乘性噪声污染时，FCM、CsiFCM、siibFCM以及本文算法对实验中所有无损检测图像的F-value平均值分别为64.78%、67.90%、69.41%、88.50%。另外，FCM、CsiFCM、siibFCM以及本文算法对实验中所有无损检测图像的G-mean平均值分别为84.81%、81.47%、83.07%、93.83%。F-value和G-mean指标优于对比算法的主要原因是本文采用了条件值表征样本容量来平衡不同大小的类群，因此提升了对少数类的聚类性能。

从表2和图4(a)中可以看出，当无损检测图像被污染时，本文算法的聚类性能要优于对比算法。但是当无损检测图像没有被污染或者当图像被非均匀分布的瑞利噪声污染时，本文算法性能与对比算法基本一致或者稍微弱于对比算法。其主要原因是本文算法采用了对图像中少数类加权的策略，尤其是针对非均匀噪声的攻击，在增强了少数类权重的同时也增加了该区域的噪声强度，导致本文算法对部分图像(如Im6)的聚类性能略微低于对比算法。

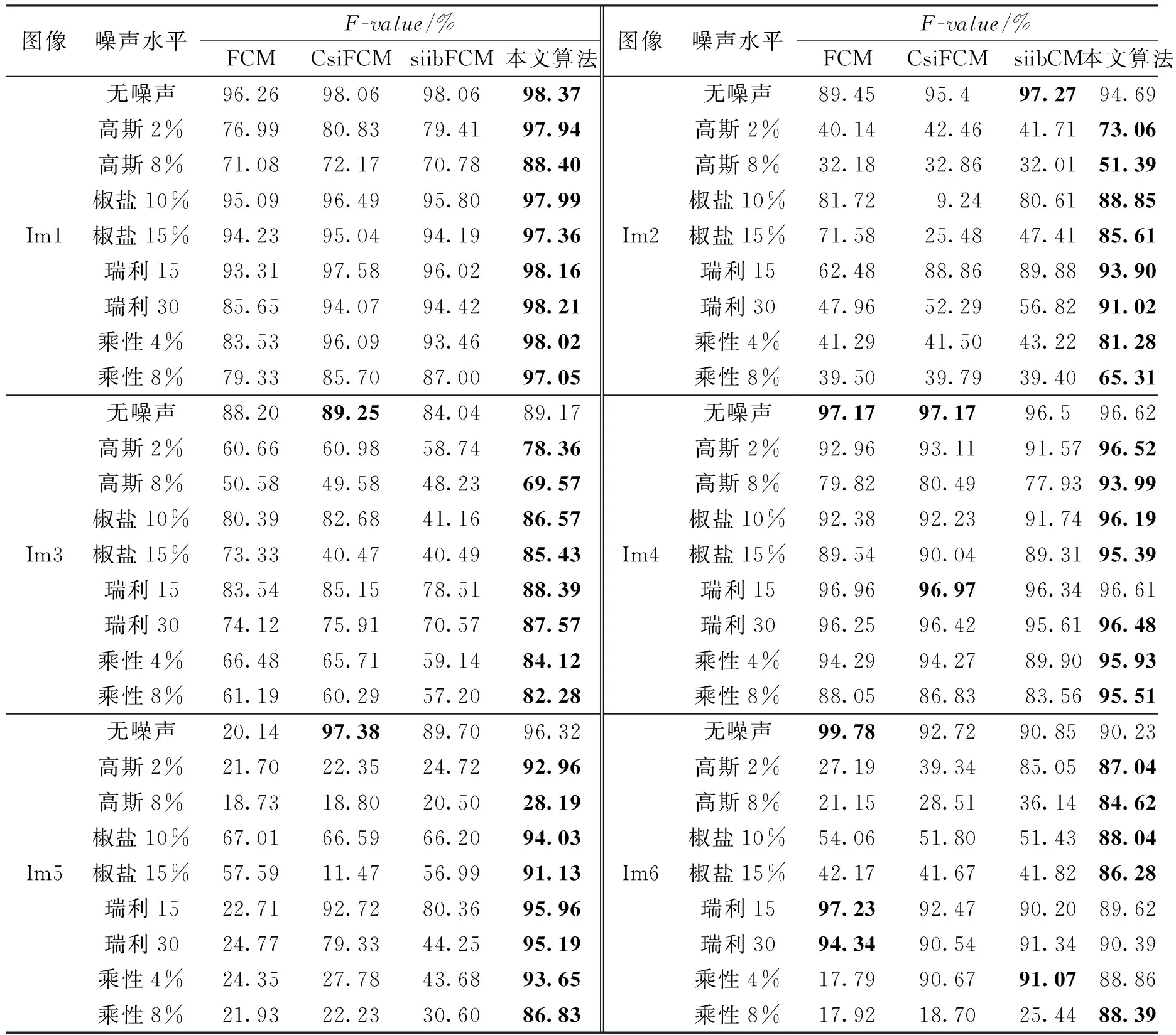
表2 不同算法得到的F-valueTable 2 F-value obtained by different algorithms

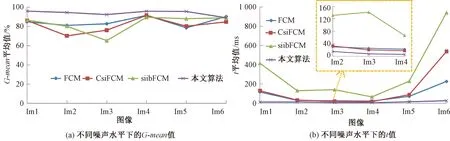
图4 不同算法得到的G-mean和TimeFigure 4 G-mean and Time obtained by different algorithms

图4(b)为本文算法和对比算法对无损检测图像在不同噪声水平下分割时间平均值对比图。可以看出，本文算法的分割速度更快，本文算法对实验中所有无损检测图像分割时间的平均值为14.06 ms。其主要原因是本文算法采用对图像的灰度级进行分类，而不是图像的像素，造成了当图像的尺寸较小时，如Im2、Im3和Im4，本文算法只是稍优于对比算法，也说明本文算法适合图像尺寸较大的场合。

图5为本文算法与对比算法对Im5的分割效果图。其中图5(a)为原图；图5(b)为噪声污染后的图像；图5(c)为标准分割结果；图5(d)～5(g)为本文算法和对比算法的分割结果。从图5中可看出，对比算法对噪声比较敏感，而本文算法鲁棒性较高，受噪声的影响较小，分割效果优于对比算法。其主要原因是本文算法引入局部空间信息和灰度信息对图像进行预处理，提高了算法的鲁棒性。

图5 Im5图像及其各算法的分割结果Figure 5 Comparison of segmentation results on non-destructive testing Im5

4 结论

为了改善模糊C均值算法不能有效分割类间差异较大的图像这一问题，提出了一种新的用于分割无损检测图像的快速模糊C均值算法。该算法主要是通过引入局部空间信息和灰度信息，降低噪声的影响，用条件值表征样本容量来平衡不同大小的类群，避免较小类群的聚类中心向较大类群偏移。基于新的约束条件得到新的隶属度和聚类中心表达式，对预处理后图像的灰度级进行分类，大幅度地降低了算法的时间复杂度。实验数据证明了本文算法的有效性和鲁棒性。下一步研究可改进算法对非均匀噪声的处理及初始化方式，以便更加有效地对不平衡图像数据进行精细的分割。