《兴和历》行星算法及精度

贺 楠

（西北大学 科学史高等研究院，陕西 西安 710127）

行星运动理论是中国古代历法的重要内容之一，从汉代《太初历》始就有比较系统的行星运动算法。两汉至隋代的行星理论涉及的算法较少，算法也相对简单。尽管如此，这个时期各部历法中的行星理论仍旧受到科学史家的关注。薄树人讨论了《太初历》和《三统历》两部历法的关系，并对《三统历》中的行星算法进行了整理和分析[1-2]。杨帆和孙小淳以火星为例，考察了从《三统历》到《皇极历》火星视运动动态表的历程[3]。钱宝琮、薮内清综述了从春秋到明末的历法沿革，梳理了魏晋南北朝的历法[4-5]。张培瑜、陈美东等人研究了中国古代历法的算法原理[6-7]。曲安京主要分析了隋代之前传统历法中行星平运动推算的精度[8-10]。唐泉介绍了我国古代行星理论的历史沿革和基本思想，指出了该领域尚未解决的问题和未来努力的方向[11-13]。以上学者对于我们认识中国古代早期历法中的行星理论做了重要的工作，但是关于隋代之前行星计算精度讨论尚不多见。

北魏孝明帝于正光三年（522）下诏颁行张龙祥和李业兴等九家共修的《正光历》。东魏孝静帝在迁都邺城不久，发现行用的《正光历》推算节气、朔和五星位置不准。兴和元年（539），孝静帝命李业兴改历，李业兴在《正光历》的基础上，两个月内修订完成新历《兴和历》，尚书左仆射司马子如与右仆射高隆之将新历进献给孝静帝。《兴和历》于兴和二年（540）颁行，行用10年，直到东魏统治结束。虽然《兴和历》在中国历法史上并无多大创新，且是在《正光历》基础上修订而成，行用时间也不长，但参与历法改革的人众多，其中包括许多高级别行政官员及改历技术人员如大丞相主簿孙搴、太史令赵洪庆及精通天文星占的王春等人。尤其值得关注的是，在《兴和历》颁行前期，信都芳和历法制定者李业兴曾围绕《兴和历》行星计算精度进行过论争，最后李业兴通过比较指出“旧历（《正光历》）差天为多，新历（《兴和历》）差天为少”，肯定了《兴和历》在行星位置推算方面的进步性。

本文将根据《兴和历》行星算法术文，试图用计算机程序模拟《兴和历》推算行星位置算法，讨论《兴和历》行星计算精度，并对影响《兴和历》行星计算精度的原因进行分析。

1 《兴和历》“步五星见伏术”的常数及动态表

根据《魏书·律历志》记载，《兴和历》共分七章，“步五星见伏术”为第七章。在讨论行星算法之前，我们首先给出《兴和历》“步五星见伏术”中使用的天文常数。

“蔀法，一万六千八百六十；度法，一万六千八百六十”：蔀法，又名度法，《兴和历》将一天分为16 860分，满16 860分即为1度（日）。各种与时间有关的周期常数以“蔀法（度法）”作分母。

“周天，六百一十五万八千一十七”：《兴和历》未引入岁差，所以恒星年长度与回归年长度一致。

“斗分，四千一百一十七”：《兴和历》将太阳一年运行一周天365度的余分4117称作斗分。

“火数，一千三百一十四万九千八十三；合终日数，七百七十九；合终日余，一万五千一百四十三”：分别为以“分”为单位的行星会合周期，以“日”为单位的会合周期长度的整日数及不足一“日”的时间。以火星为例：火星的会合周期=合终日数

下面以火星为例，考察《兴和历》中火星在一个会合周期的运动状态，其术文称：

荧惑：晨与日合，在日后伏，七十一日、日余一万六千一，行星五十五度、度余一万三千九百四十三。晨见东方，顺，疾，日行二十三分之十四，一百八十四日行一百一十二度。顺，迟，日行十二分，九十二日行四十八度而留。不行，十一日而旋。逆，日行六十二分之十七，六十二日退十七度。复留，十一日。复顺，迟，日行十二分，九十二日行四十八度。复顺，疾，日行十四分，一百八十四日行一百一十二度。在日前，夕伏西方，顺，七十一日、日余一万六千二，行星五十五度、度余一万三千九百四十三，而与日合。[14]1844

行星在恒星背景中呈现顺逆、迟疾、留等十分复杂的现象，其运动速度也有快有慢。为了更好地刻画行星在一个会合周期内的运动，中国古代历法家通常采取分段方案，将行星在一个会合周期内的运动划分为许多段目，并给出行星在各段运行的时间、速度及运行的度距。而且行星在每个会合周期内的运行都是重复的。

《兴和历》五星动态表均是以“合”作为起点，当火星与日相会时，称为“合”。“合”是中国古代五星动态表中的一个重要关键点，是历法家计算五星位置的起算点。在北朝天文学家张子信发现五星和太阳不均匀性运动现象之前，历法家按照五星和太阳均匀运动推算出来的“合”只能称“平合”。根据术文，可将火星在一个会合周期内的运动状态列为表1。

表1中，平行率为行星在各段目内的平均速度，段日为行星在各段目运行的日数，行度为行星在各段目运行的度数。《兴和历》中木星、火星、土星的动态表类似，但两个内行星分别用两段文字描述其运动，分别以晨合和夕合为起点，相继给出了行星在每段运行的段日、平行率及行度。

表1 《兴和历》火星动态表

2 《兴和历》行星算法释读

《兴和历》中行星算法，按顺序逐条编号，共计7个算法，刘洪涛与王应伟对其所有算法进行了详细解读[15-16]，本文仅解读关于行星位置的核心算法，并用现代数学公式表达原文所述的计算法。

2.1 推算行星与日合时的位置

（1）推五星术。[14]1842该术文目的是推算所求年天正冬至太阳运行至行星与日合时的时距，由于日行一度，所求年天正冬至太阳运行至行星与日合时的度距与时距数值上相等。

对于金水二星，会合周期有二合，一为晨合，一为夕合。用式（3）判断所求年天正冬至后的内行星与日首次合为晨合或夕合。

由于术文中记载《兴和历》冬至时太阳在牛前十二度即斗14.25度，依次过宿去之，算外，得所求年天正冬至后的行星与日合时入某宿宿度。

（2）求后合度术[14]1843。该术文目的是推算行星再合时入某宿某度。

基于“推五星术”的算法，以五星在一个会合周期运行的度数加之，可得行星与日再合时的位置。

2.2 推算行星与日合时的日期

（1）求星合月及日术[14]1843。该术文目的推算冬至后第一次星合所在月及日。

（2）求后合月及日术[14]1843。该术文目的推算冬至后第二次星合所在月及日。

基于“求星合月及日术”算法，以五星在一个会合周期运行的日数加之，可得行星与日再合时的日期。

对于内行星，有晨合与夕合，若初合在晨合，再合为夕合；若初合在夕合，再合为晨合。

企业销售商品赠送有偿取得的其他物品，在用友U8 V10.1财务软件中业务核算流程与销售赠送同类商品有所不同。企业购入其他物品时已明确用途作为赠品免费赠送，因此，应将其单独入库，且采购成本直接计入“销售费用”；而发出时，将已计入进项税额的增值税作为进项税额转出。下面将从专门采购赠品、销售发放赠品两个角度阐述在用友U8 V10.1财务软件中的业务核算流程。

2.3 根据行星动态表推算行星每日的位置

求五星行所在度术[14]1847。该术文目的推算五星某日行某度。

3 《兴和历》行星算法算例分析及程序实现

参照本文第2 节《兴和历》五星推算思路，给出539年火星赤道宿度的算例。

根据《兴和历》术文算理可得N593T≡r（mod 60），将上元距兴和元年（539）的积年N539=293 996年等数据代入，得到冬至大小余r的整数部分冬至大余10，冬至小余0.126 5日。根据60甲子的纪日表，记甲子所在日干支序号为0，从乙丑所在日干支序号为1开始算起，第10个干支名为甲戌，则兴和元年冬至时刻日期为十一月“甲戌”12.65 刻（539 年12 月20 日3 时2 分），查张培瑜《三千五百年历日天象》[17]，539 年理论冬至时刻日名是“甲戌”（539 年12 月20 日1 时57分），历法冬至比理论冬至推后了1小时5分。

（1）推五星术。即计算兴和元年（539）冬至时刻距火星与日合时的时距，确定冬至后第一次火星与日合时的位置。

根据第2节公式（1）（2）代入数据可得：

则兴和元年（539）冬至时刻距火星与日合时的时距为728日，由于日行一度，太阳从兴和元年（539）冬至时刻运行至火星与日合时的度距也为728度。

已知《兴和历》“推五星术”术文记载冬至时太阳在牛前十二度即斗14.25度，借助二十八宿距度表①《兴和历》中各宿名称及度数为：东方苍龙七宿（七十五度）：角十二、亢九、氐十五、房五、心五、尾十八、箕十一；北方玄武七宿（九十八度分四千一百一十七）：斗二十六、牛八、女十二、虚十、危十七、室十六、壁九；西方白虎七宿（八十度）：奎十六、娄十二、胃十四、昴十一、毕十六、觜二、参九；南方朱雀七宿（一百一十二度）：井三十三、鬼四、柳十五、星七、张十八、翼十八、轸十七。，则斗宿尚有11度，减之，所得350度，继续减其余宿宿度，则火星与日合时入斗宿11度。

（2）求星合月及日术。即推算兴和元年（539）冬至后首次火星与日合所在月及日。

首先由“步月朔弦望术”中的“推积月”“推积日”算法及“步二十四气闰术”中的“推二十四气术”确定“冬至去朔日数，减一”为22日②“冬至去朔日数，减一”涉及《兴和历》第一章节的内容，由于篇幅有限，本文没有给出计算过程，只列出结果。。将冬至小余、合度余等代入式（5），可得

（3）求五星行所在度术。即计算火星与日合后每一日夜半行星位置。

在理论冬至时刻的太阳赤经270°的基础上，求得公元539 年历取冬至时的太阳赤经为δ=270.0608°，由火星从冬至时刻到火星与日合时运行的度数是728度，从而得到火星合所在日的赤经β。

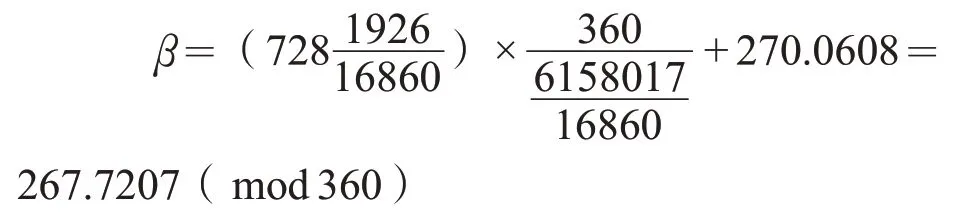
由于在合时刻不能确定行星能被观测到，所以我们计算合所在日夜半时刻行星的位置。已知公元539 年冬至时刻距离火星与日合时的时间长度为728.1142日，冬至小余为0.1265日，则火星与日合时距前一个冬至夜半的时间长度为728.2407 日，从而火星合所在日夜半时刻的赤经β′为

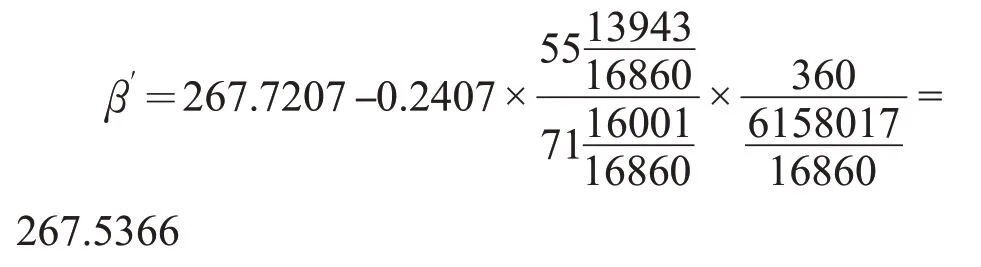
借助五星动态表，根据“求五星行所在度术”推求各段的合时刻及合之后每一日夜半的火星赤经值。对于木星、火星、土星、金星、水星分别计算兴和元年（539）冬至后27、14、29、19、96 个完整的会合周期内每一天的夜半的位置。为了更清楚地考察《兴和历》行星计算精度，我们分别给出五星的计算误差数据，并进行分析汇总如表2。

表2 《兴和历》539—568年间行星计算精度

为了更直观地考察《兴和历》中的行星计算精度，我们运用计算机Python 软件将这部历法的推五星算法程序化，利用数据绘制出五星绝对误差（历法值—理论值）散点图（图1-5）。图中横坐标均表示行星从合时刻当日夜半起算的日数，单位为“日”，横坐标分别始于540 年3 月10 日夜半、541 年12 月18日夜半、540年10月7日夜半、540年10月22日夜半、539 年12 月23 日夜半。纵坐标表示行星赤经误差（历法值-理论值），单位为“°”①在程序算法中，已将古度转为现代度，转换公式为365.24古度=360°。。五星在行用初期的首个会合周期中的绝对误差最大值分别为8.71°、20.50°、7.12°、9.25°、4.62°。为了全面考察行星计算精度，按照《兴和历》行星算法计算木星、火星、土星、金星、水星从行用时间起30年内每一日夜半的赤经，并与行星的理论位置作了误差比对。

图1 木星赤经绝对误差（历法值-理论值）散点图

图2 火星赤经绝对误差（历法值-理论值）散点图

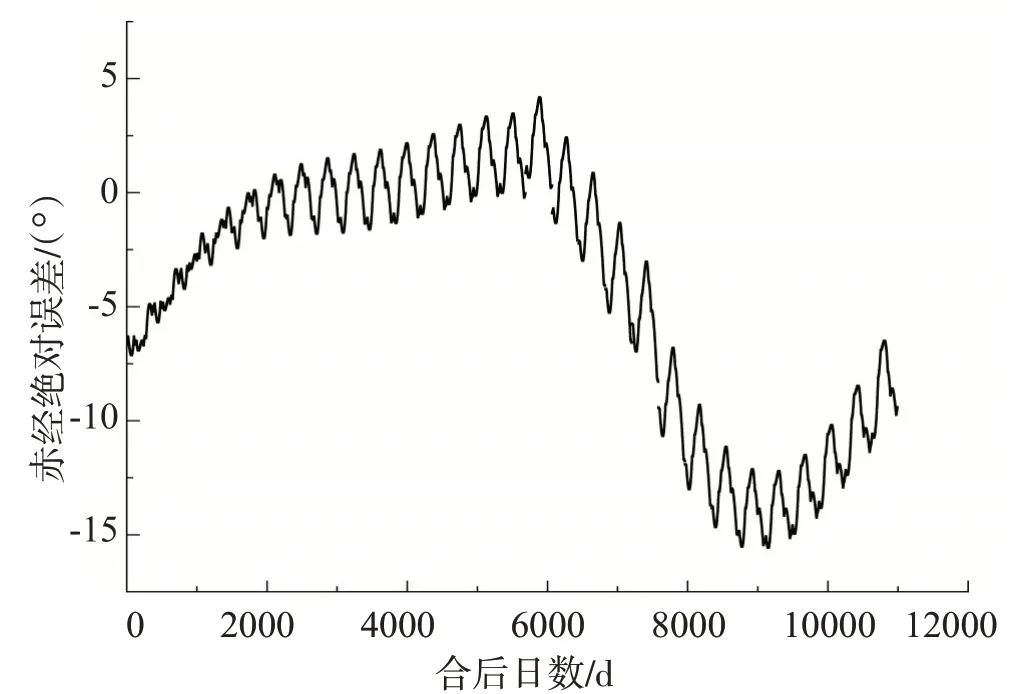
图3 土星赤经绝对误差（历法值-理论值）散点图

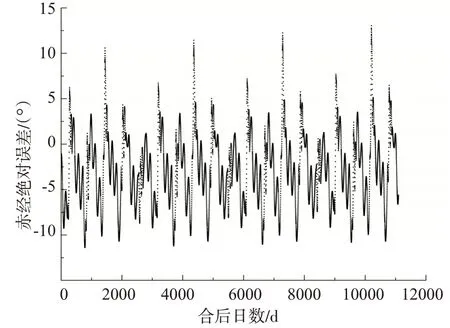
图4 金星赤经绝对误差（历法值-理论值）散点图

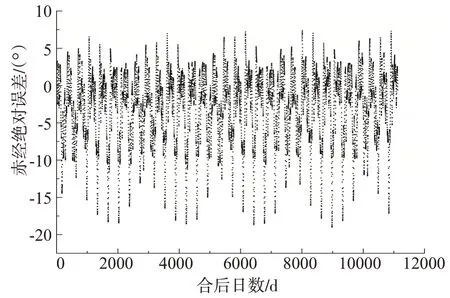
图5 水星赤经绝对误差（历法值-理论值）散点图

4 《兴和历》行星精度误差分析

影响行星计算精度的因素有很多，如行星中心差算法、天文常数的精度、起点的推算误差、天文算表精度、算法设计是否合理、等多种因素。其中行星中心差算法是影响行星计算的最大因素，不过在北齐天文学家张子信发现太阳和行星不均匀性运动之前，汉代至魏晋南北朝的历法均未考虑过太阳与行星修正。从隋初《皇极历》开始才参考张子信的重大发现，考虑设计行星与太阳中心差算法来修正行星平运动。

4.1 《兴和历》行星会合周期的精度

我国早在先秦时代就有了五星会合周期的概念，其中历代历法大都直接给出五星会合周期的具体数值。如《兴和历》有关五星会合周期的记载：

木精曰岁星，其数六百七十二万三千八百八十八。火精曰荧惑，其数一千三百一十四万九千八十三。土精曰镇星，其数六百三十七万四千六十一。金精曰太白，其数九百八十四万三千八百八十二。水精曰辰星，其数一百九十五万三千七百一十六。[14]1842

《荆州占》：“五星者，五行之精也”。[18]按照五行学说，岁星为木精，故称木星；荧惑为火精，故称火星；填星为土精，故称土星；太白为金精，故称金星；辰星为水精，故称水星。表3给出《兴和历》五星会合周期和理论值及其误差。

表3 《兴和历》五星会合周期和理论值及其误差

上述“其数”为五星的会合周期，单位“分”，若以“蔀法”（16860）除之，转化为单位“日”。《兴和历》的木星、火星、土星、金星、水星误差日数分别为0.076 9、0.038 2、0.033 7、0.061 2、0.007 5 日。其中水星周期误差最小，火星、土星、金星次之，木星的周期误差最大。关于我国五星会合周期的精度演变情况，已有学者做过深入讨论[19-20]。

4.2 《兴和历》平合日期推算误差

根据算法“推五星”“求星合月及日术”“求后合月及日术”确定行星与日平合日期。查刘次沅的古代黄道星空软件可知历取合儒略日序号和理论合儒略日序号。以火星为例，如539年，按照《兴和历》算法求出火星与日平合日期为541年12月18日，历法儒略日序号为1919010。查古代黄道星空软件中火星与日赤经相合时，赤经误差最小的日期为541 年12 月2 日，儒略日序号为1918994，可知火星历法合与理论合时间存在15日的误差。

依照此理，《兴和历》木星、火星、土星、金星、水星与日合日期与理论日期最大误差天数分别为9、21、11、10、10日。平均误差天数为4.6、11.3、6.1、2.7、7.7日。其中火星合误差日数最大，高达20多日。其余四星的合最大误差日数均在10日左右。火星和水星平均误差在10日左右，由于火星水星相对难观测，误差较大。木星、土星、金星平均误差也在2～7 日。根据五星平合日期的推算结果，可知起点的推算也存在较大的误差。

4.3 《兴和历》在一个会合周期速度误差

利用行星动态表中的数据，构建出《兴和历》的行星运动状态表的理论速度与历取速度折线对比图（图6-10）。行星动态表中每段目行星行度及所行日数可得火星历取每段平行率，得出五星在一个会合周期的历取速度，见图中的实线。利用Skymap 提取行星在任何时刻的位置，计算出以“合”为起点行星的实际运动速度，见图中的虚线。

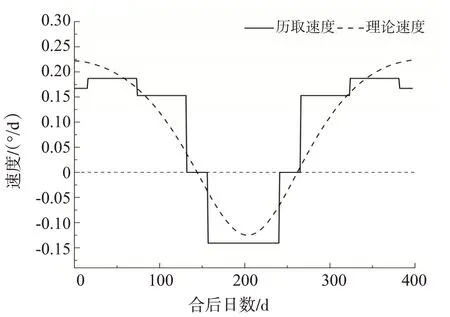
图6 木星历取速度与理论速度折线图

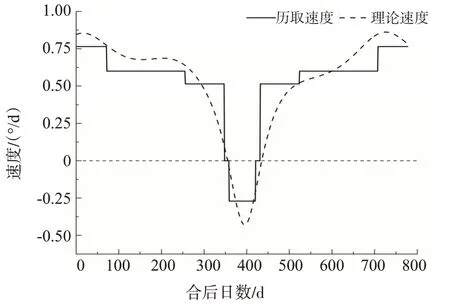
图7 火星历取速度与理论速度折线图

图8 土星历取速度与理论速度折线图

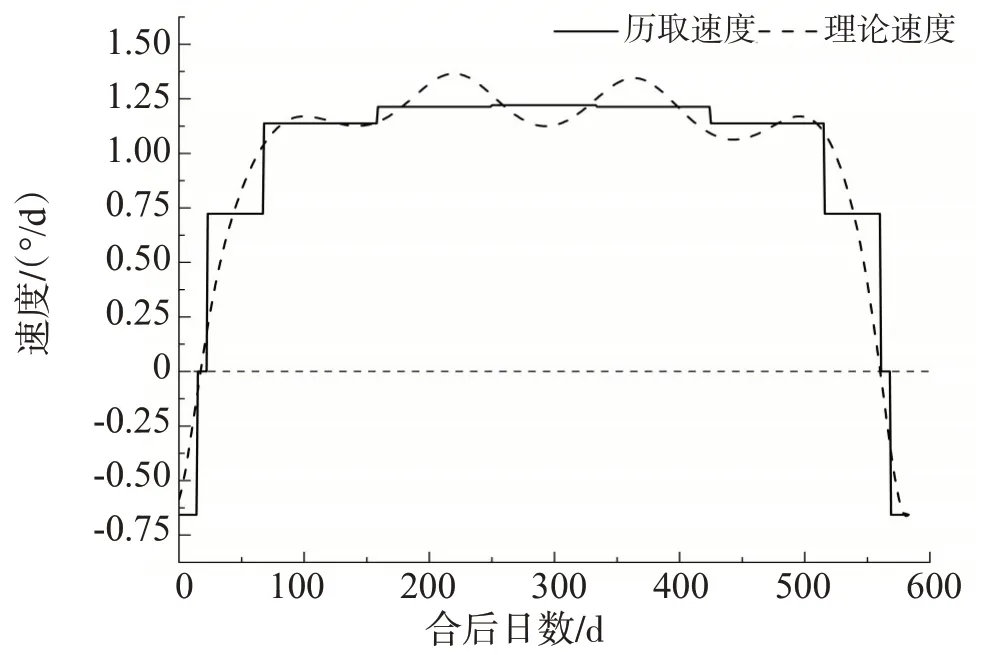
图9 金星历取速度与理论速度折线图

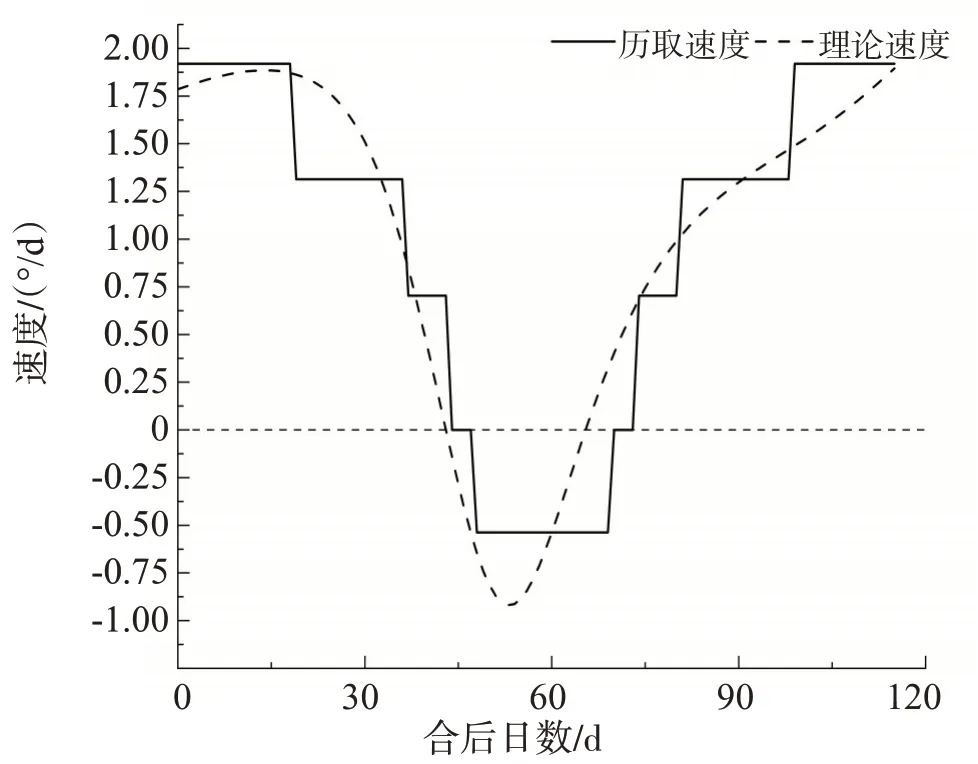
图10 水星历取速度与理论速度折线图

早期历法行星动态表的文字描述都比较粗糙，段目划分也较为稀疏。以《兴和历》的木星、火星、土星、金星、水星为例，比较图中的虚线和实线，可以直观地看出《兴和历》所给的行星动态表中描述行星在一个会合周期内历取运动与实际运动符合的程度。图6-10 表明五星历取速度与理论速度在一个会合周期中呈现对称结构，总体上比较规整，但五星在一个会合周期内历取速度与实际速度吻合还是不完全一致的，可知会合周期的各段目速度的构造也是影响计算精度的因素之一。

4.4 《兴和历》行星动态表精度

唐泉在讨论中国古代五星动态表时，构造了以“合”为起点的行星动态表的数学模型[21]，利用该模型，我们可以分析《兴和历》动态表的精度。以《兴和历》火星的动态表精度误差表（表4）为例，其中的“段日”“历取积度”均为火星动态表所给，分别意为火星在各个段目运行的日数及度数，“理论积度”为应用唐泉构造理论公式计算的结果，继而得到行度误差（历法积度-理论积度）与各段目节点误差值。

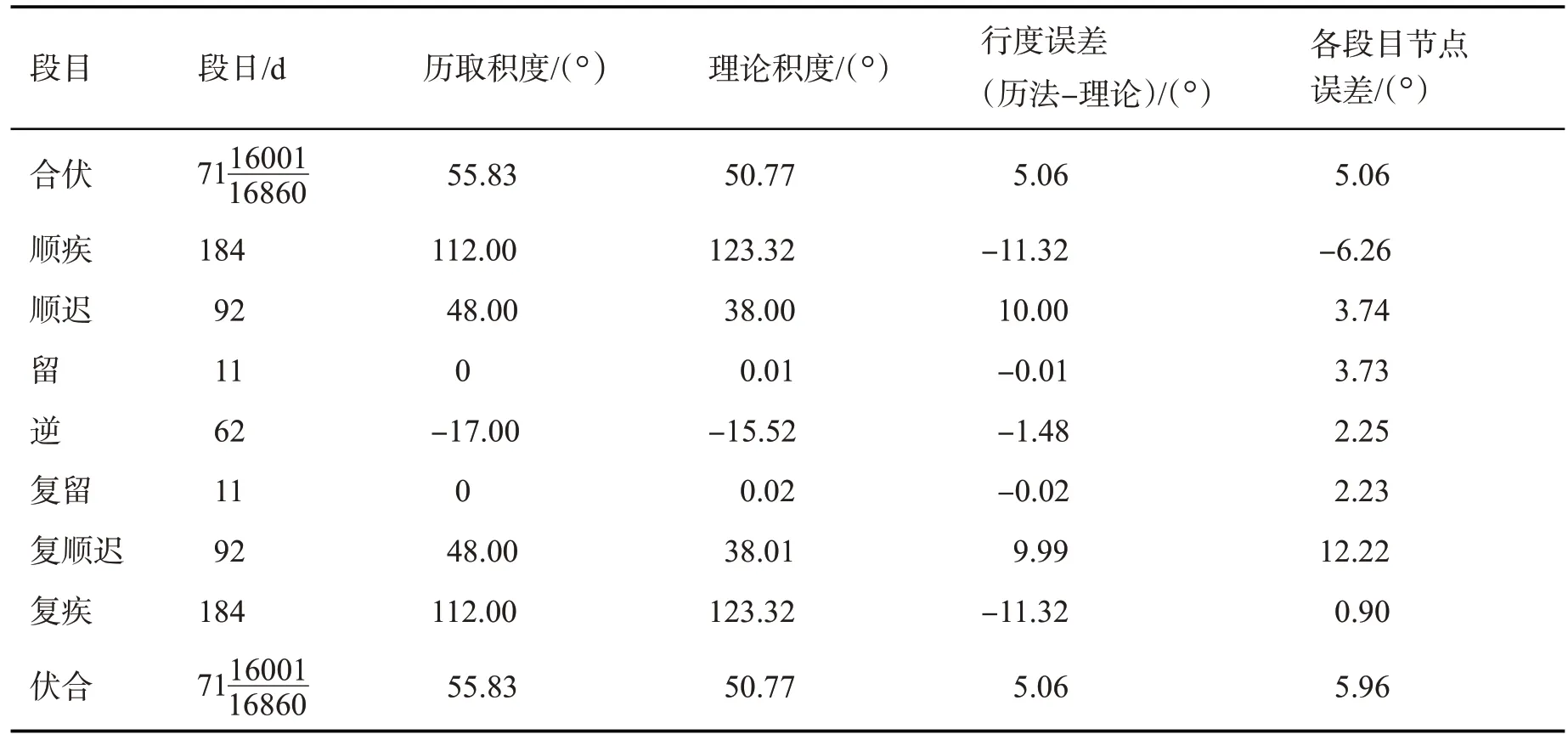
表4 《兴和历》火星动态表精度误差

依据理论公式可得，《兴和历》行度绝对值最大误差为木星于逆段3.14°、火星顺疾段11.32°、土星逆行段0.21°、金星顺行段4.33°、水星合伏及顺行段2.54°。各段目节点绝对值最大误差分别为木星2.19°、火星12.22°、土星0.19°、金星8.62°、水星2.54°。综上所述，土星的动态表精度最优，木星、金星、水星次之，火星的动态表精度最差。

5 结语

从算法上讲，《兴和历》的“步五星见伏术”是基于前历《正光历》而得，行星算法上并未有实质性的创新，且隋唐之前的行星理论均未考虑太阳和行星中心差。一直到北齐张子信发现行星运动的不均匀性之后，我国古代历法才开始设计算法进行修正，故隋唐之前的行星计算精度基本处于同一水平。从时间上讲，《魏书·律历志》中记载《兴和历》是在短短两个月内就完成了历法的制定，可见制历者水平之高。本文通过对《兴和历》行星位置核心算法的解读，讨论了关于行星计算位置精度及误差产生的原因，根据分析发现：

（1）对《兴和历》的行星计算而言，五星位置算法基本相同。在《兴和历》行用期间（539—568），外行星木星、火星、土星的绝对平均误差分别为3.11°、6.16°、3.88°；绝对误差最大值分别为15.26°、40.95°、15.58°。根据现代天文知识，木星、火星和土星的轨道偏心率分别为0.048、0.093、0.055。火星的轨道偏心率较大，周期也长，因此从理论上讲，火星的计算要比木星和土星困难一些，故火星的计算精度最差，土星次之，木星最优。内行星金星、水星的绝对平均误差2.26°、3.16°，最大误差分别为13.04°、19.00°。轨道偏心率分别为0.007、0.206，相较于金星，水星的轨道偏心率较大，计算上稍显复杂，精度也劣低于金星。

（2）通过本文分析行星会合周期精度、平合日期误差，五星在一个会合周期历取与理论速度精度以及动态表构造精度来分析影响行星位置的推算。按照历法所给五星会合周期（表3）及行星算法求出平合日期的结果，可知五星起点的推算就存在较大的误差。过构造的行星在一个会合周期的速度误差折线图（图6-10）及动态表的精度分析结果（表4）显示两者也在影响五星的位置精度。

（3）魏晋南北朝的历法，五星的预报有所进步。历法家提出了以任一日五星所在宿度为验的新手段。《魏书·律历志》中记载信都芳曾于兴和元年（539）十二月二十日，对李业兴的《兴和历》五星法与实测进行比较，发现木星差二度，土星差五度，金星差四度。李业兴承认新历（《兴和历》）推算五星位置还存在较大的误差，不过在与旧历（《正光历》）进行比较后，信都芳肯定了“旧历差天为多，新历差天为少”的事实，确认《兴和历》在五星推算方面仍有一定进展的事实。以上表明，我国古代历法的选用或废止，都经过了激烈的争论，并且解决争端的基本方法是接受实际天象的检验，尤其是关乎于行星位置。