基于R软件的数字金融发展对企业金融资产投资的影响分析

刘可馨，刘高生，赵静文

(1.天津商业大学 理学院，天津 300134； 2.天津城建大学 经济与管理学院，天津 300384)

1 分位数回归模型

分位数回归模型[1]将数据按因变量拆分成多个分位数点，研究不同分位点情况下的回归影响关系情况。分位数回归主要有两个作用：一是分析不同分位数条件下自变量对于因变量的影响关系；二是分位数回归模型具有稳健性。由于模型中可能存在异常值、异方差等问题，会导致回归结果出现偏差，通过线性回归模型无法了解自变量对于因变量的影响关系，因此建立分位数回归模型，可以很好地解决异常值及异方差等问题[2-3]。

2 R软件中的模型实施过程

R软件是开源、免费统计软件，R软件及其软件包都很容易得到。由于研究者可提交软件包，许多前沿统计方法均可在R软件中实现。本研究给出了数字金融发展对企业金融资产投资的影响程度分析的R软件实施过程。利用glmnet()函数进行lasso变量选择，利用step()函数进行再次变量选择，利用lm()函数建立多元线性回归模型，由于残差为非正态分布，利用rq()函数建立分位数回归模型。

2.1 主要函数说明

lasso函数：glmnet()函数，通过惩罚的最大似然拟合广义线性模型。函数用法：glmnet(x,y,…)。主要参数：x每行都是一个观测向量，可以采用稀疏矩阵格式；y是响应变量。cv.glmnet()，对 glmnet 进行 k 折叠交叉验证，生成一个绘图并返回一个值，函数用法：cv.glmnet(x,y,…)。

逐步回归函数：step()函数，通过AIC选择基于公式的模型。函数用法：step(object, scope, scale=0,direction=c(″both″, ″backward″, ″forward″), trace=1, keep=NULL, steps=1000, k=2,…) 。主要参数：object用作逐步搜索中的初始模型，如“lm”。Scope是在逐步搜索中检查模型范围。Scale是定义AIC统计量时用于选择模型。

多元线性回归函数：lm()函数。函数用法：lm(formula,data,subset,weights, na.action,method =″qr″,model=TRUE,x=FALSE,y=FALSE,qr=TRUE,singular.ok=TRUE,contrasts=NULL,offset,…)。 主要参数: formula是要拟合的模型符号描述，data是包含模型中变量的可选数据框、列表或环境。

分位数回归：rq()函。函数用法：rq(formula, tau=.5,…)。主要参数：formula是一个公式对象，tau是要估计的分位数，通常是介于0和1之间。

2.2 应用实例及解释

2.2.1 建模步骤

为研究数字金融发展对企业金融资产投资的影响，以企业金融资产投资为因变量，选择的控制变量[4-5]依次为：x1：企业规模，以总资产的自然对数表示；x2：企业资产负债率，以总负债占总资产的比重表示；x3：资产收益率，即公司净利润与总资产之比；x4：经营性现金流，以经营性现金流量净额与总资产之比表示。核心自变量指标，x5：时间变量，x6:数字金融发展水平[6]。采用北京大学普惠数字金融指数省级层面指数来表示。所用数据为2011-2018年A股上市公司的经营活动相关的年度数据，数据来源于国泰安数据库。

第一步：读入数据，设置所需要的自变量，并对自变量进行预处理。read()读入数据，将数据中的自变量设为x1，x2，x3，x4，x5，x6；scale()函数对数据进行标准化处理。第二步：进行lasso回归。cv.glmnet()对自变量及其交叉项进行lasso回归；plot()画出回归图。第三步：对lasso回归中的自变量进行逐步回归，选择最优变量。step()进行逐步回归，利用AIC最小准则，选出显著性最好的变量。第四步：对上一步得出的最优变量进行多元线性回归。lm()进行拟合。第五步：对线性回归的方程进行残差分析。第六步：进行分位数回归。rq()函数进行分位数回归。

2.2.2 实证分析及结果展示

加载需要的包。需要的函数包主要为glmnet包、corrplot包及quantreg包。代码如下：library(corrplot); library(SparseM); library(quantreg);library(Matrix);library(glmnet)。

读取数据，对数据进行标准化处理再进行分析。lasso回归进行变量选择，采用cv.glmnet()函数对自变量及其交叉项进行lasso回归，代码如下：

xx=cbind(x1,x2,x3,x4,x5,x6,x1*x6,x2*x6,x3*x6,x4*x6,x5*x6,x6*x6)

fit=cv.glmnet(xx, fin_asset)

lambda.optimal=fit$lambda.min

coef(fit, s=lambda.optimal)

输出结果为：

13x1 sparse Matrix of class ″dgCMatrix″

s1(Intercept) -0.013778022V1 -0.407741047V2 0.237473071V3 0.046858447V4 -0.005865020V5 0.080697212V6 0.027976089V7 -0.049587383V8 0.027701505V9 0.004126360V10 -0.003231403V11 . V12 0.016716786

根据lasso回归结果显示，去掉了变量x5*x6，保留了其余的11个变量。通过corrplot函数发现自变量之间仍存在相关性，因此利用step函数再次选择自变量，代码如下：

fit_step=step(lm(fin_asset～x1+x2+x3+x4+x5+x6+x1*x6+x2*x6+x3*x6+x4*x6+x6*x6),direction=″both″)

输出结果(仅保留部分结果)：

Step: AIC=-2468.59

fin_asset～x1+x2+x3+x5+x6+x1:x6+x2:x6

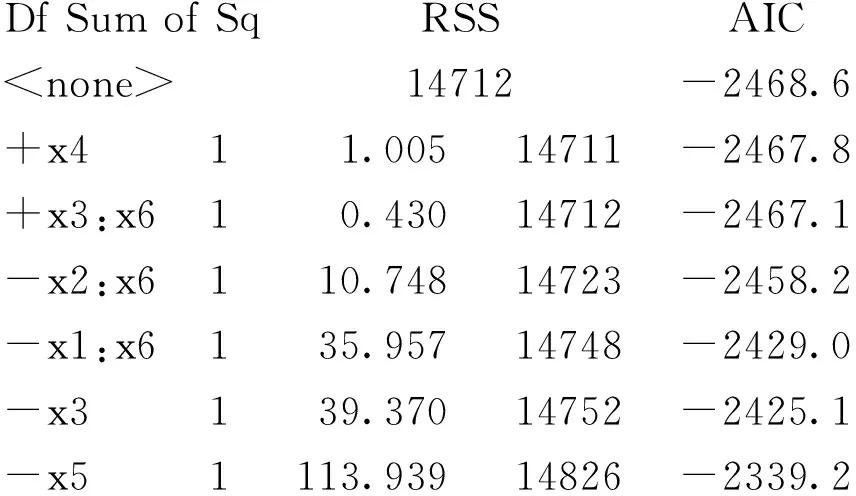
Df Sum of Sq RSS AIC 14712 -2468.6+x4 1 1.005 14711 -2467.8+x3:x6 1 0.430 14712 -2467.1-x2:x6 1 10.748 14723 -2458.2-x1:x6 1 35.957 14748 -2429.0-x3 1 39.370 14752 -2425.1-x5 1 113.939 14826 -2339.2

利用AIC最小准则，选出显著性最好的变量为x1、x2、x3、x5、x6、x1*x6、x2*x6。定义所选的自变量为X，corrplot函数发现自变量之间相关性较若，主要代码如下:

X=cbind(x1,x2,x3,x5,x6,x1*x6,x2*x6)

corrplot(cor(X),method=″color″)

对上一步得出的最优变量进行多元线性回归。利用lm()函数建立多元线性回归模型，代码如下：

lmmode=summary(lm(fin_asset～X))

输出结果为：

Call:

lm(formula=fin_asset～X)

Residuals:

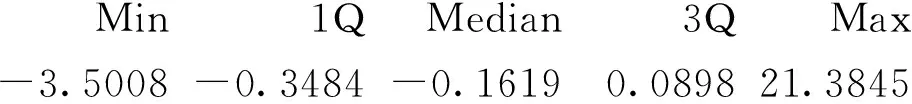
Min 1Q Median 3Q Max -3.5008 -0.3484 -0.1619 0.0898 21.3845

Coefficients:

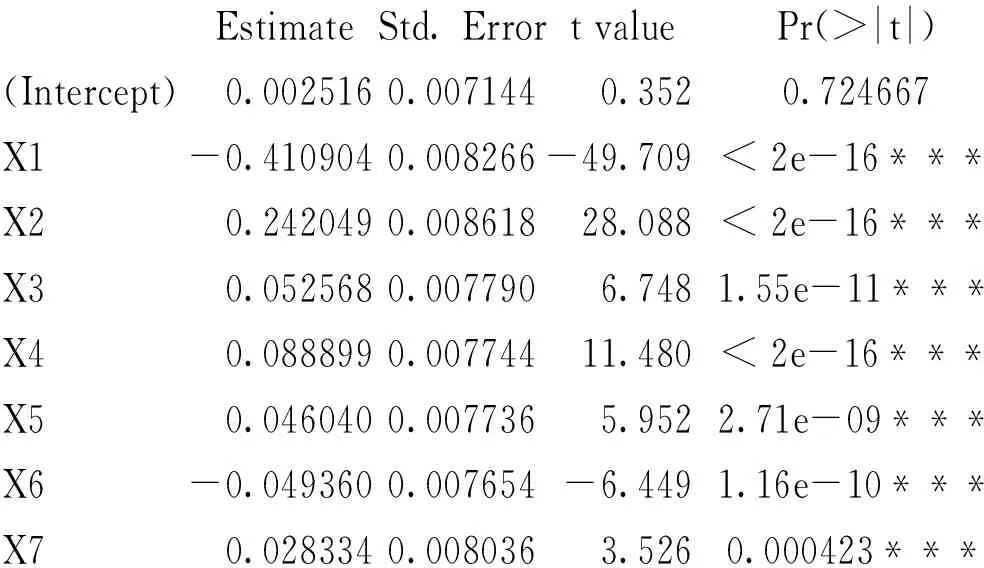
Estimate Std. Error t value Pr(>|t|) (Intercept) 0.002516 0.007144 0.352 0.724667 X1 -0.410904 0.008266 -49.709 < 2e-16***X2 0.242049 0.008618 28.088 < 2e-16***X3 0.052568 0.007790 6.748 1.55e-11***X4 0.088899 0.007744 11.480 < 2e-16***X5 0.046040 0.007736 5.952 2.71e-09***X6 -0.049360 0.007654 -6.449 1.16e-10***X7 0.028334 0.008036 3.526 0.000423***

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9298 on 17016 degrees of freedom

Multiple R-squared: 0.1357, Adjusted R-squared: 0.1354

F-statistic: 381.8 on 7 and 17016 DF, p-value: < 2.2e-16

由结果得出P值<0.05，通过F检验，即回归方程显著，各自变量通过t检验，即所有回归系数显著。回归方程为：

fin_asset=-0.4109x1+0.2420x2+0.0526x3+0.0889x5+0.0460x6-0.0494x1*x6+0.0283x2*x6+0.0025

之后对多元回归模型得到的残差进行分析，主要代码如下：

par(mfrow=c(2,2))

plot(lmmode$residual,main=″residual″)

plot(density(lmmode$residual))

hist(lmmode$residual)

boxplot(lmmode$residual,xlab=″box plot″, main=″residual″)

由多元线性回归模型得到残差的散点图和箱线图可看出数据存在一些异常点，由密度图和直方图可看出残差是有偏的，因此采用ks函数对残差进行正态性检验，代码如下：

ks.test(lmmode$residual,″pnorm″,mean(lmmode$residual),sqrt(var(lmmode$residual)))

输出结果为：

e-sample Kolmogorov-Smirnov test

data: lmmode$residual

D=0.22526, p-value < 2.2e-16

alternative hypothesis: two-sided

由检验统计量的P值<0.05，可得拒绝原假设，即认为残差不服从正态分布，因此考虑建立分位数回归模型。利用rq()函数进行分位数回归，主要代码如下：

rqy25=summary(rq(fin_asset～X,tau=0.25),covariance=TRUE,se=″ker″)

rqy50=summary(rq(fin_asset～X,tau=0.5),covariance=TRUE,se=″ker″)

rqy75=summary(rq(fin_asset～X,tau=0.75),covariance=TRUE,se=″ker″)

输出结果以0.5分位数结果为例：

Call: rq(formula=fin_asset ～ X, tau=0.5)

tau:[1] 0.5

Coefficients:

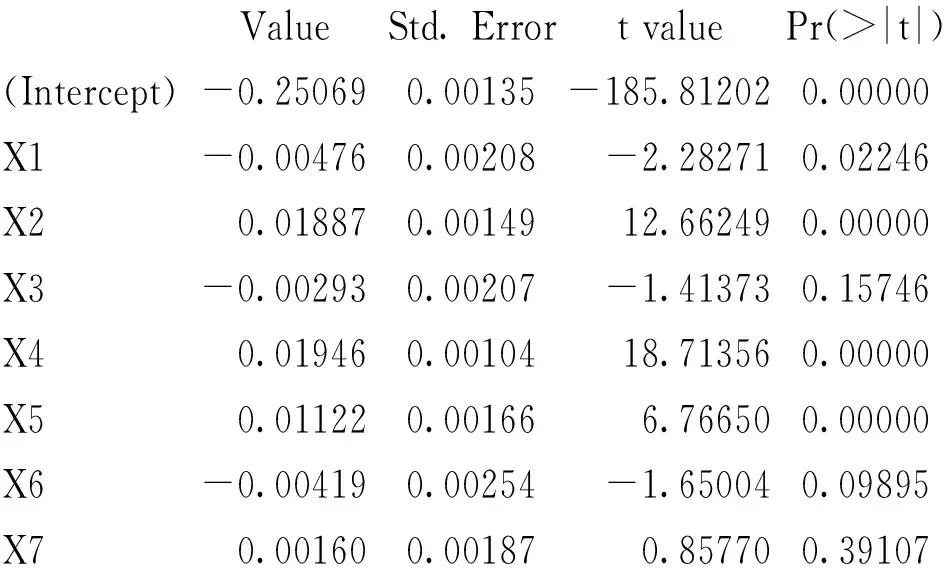
Value Std. Error t value Pr(>|t|) (Intercept) -0.25069 0.00135 -185.81202 0.00000X1 -0.00476 0.00208 -2.28271 0.02246X2 0.01887 0.00149 12.66249 0.00000X3 -0.00293 0.00207 -1.41373 0.15746X4 0.01946 0.00104 18.71356 0.00000X5 0.01122 0.00166 6.76650 0.00000X6 -0.00419 0.00254 -1.65004 0.09895X7 0.00160 0.00187 0.85770 0.39107

由结果知x1、x2、x5、x6的P值<0.05，通过t检验，其系数显著，x3、x1*x6、x2*x6的P值>0.05，未通过t检验，其系数不显著，可以通过实际分析其具有的经济学意义。通过分位数回归模型可得，在不同的分位数水平下，数字金融发展对企业金融资产投资的影响不同[7-9]。

3 结语

利用A股上市公司的经营活动数据，通过分析数字金融发展对企业金融资产投资的影响，给出了从变量选择到建立分位数回归模型的整个过程。这个过程对于利用R软件建立分位数模型具有一定的参考意义，同时根据相关结论，可以给出促进数字金融发展服务企业金融资产投资的建议。