土质滑坡失稳、运动及冲击压力物质点法模拟研究*
2022-10-06李天斌孙小平
王 升 曾 鹏 李天斌 孙小平
(地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059,中国)
0 引 言
滑坡灾害是全世界发生最为频繁的灾害之一,备受国际关注。其中流动型滑坡往往具有速度快、距离长的特点,对生命财产构成极大威胁。然而目前对于此类滑坡的预测尚面临诸多挑战。已有诸多学者(Wartman et al.,2005;Lin et al.,2006;Tohari et al.,2007;杜婷婷等,2018;李楠等,2019;孙萍等,2019;赵晓彦等,2019)采用物理模型试验来研究滑坡的失稳、运动和冲击过程。但室内试验往往受到尺度效应的影响难以复现滑坡的原位状态,而现场试验研究又成本巨大,因此通过数值分析方法深入研究滑坡失稳、运动与冲击过程对滑坡风险评价和管理具有重要意义。
目前国内外用于模拟滑坡问题的数值方法主要分为连续介质力学方法和非连续介质力学方法两大类。传统的连续介质力学方法(比如有限元方法,FEM)在模拟大变形问题时,由于网格畸形,使得计算意外结束。非连续介质力学方法(比如离散元方法,DEM)虽然对网格的依赖性较低,但是计算效率较低。因此,很多无网格方法相继出现,例如光滑粒子流体动力学方法(smoothed particle hydrodynamics,SPH)、粒子有限元方法(particle finite element method,PFEM)、物质点法(material point method,MPM)等。其中:物质点法能准确、高效地捕捉材料的大变形运动过程。相比SPH,物质点法对模型边界条件的施加更加简单。相比PFEM,物质点法的计算代价更低(Soga et al.,2016;王斌等,2017)。
物质点法是Sulsky et al.(1994)于1994年提出来的。20多年来,物质点法在模拟滑坡问题上得到了较广泛的应用。王斌等(2017)将物质点法应用于边坡的稳定性评价中,研究表明:物质点法能稳定、高效地评价边坡的初始破坏以及诱发的众多次生灾害。史卜涛等(2016)将物质点强度折减法运用到边坡的稳定性分析中,为边坡稳定性分析提供了崭新的思路。谢艳芳等(2018)基于物质点法对新磨村滑坡进行了二维的动力演化分析。孙玉进等(2018)、张巍等(2017)、Shi et al.(2019)采用物质点法构建了深圳滑坡的二维模型,从不同角度对该滑坡的运动过程和堆积特征等进行了模拟研究。Yerro et al.(2016)采用物质点法分析了由孔隙水压力增加引起的边坡稳定问题。Andersen et al.(2010)利用物质点法对边坡失稳过程及其对建筑稳定性的影响进行了分析。Xu et al.(2018)采用三维物质点法对中国红石岩滑坡的破坏和运动进行了模拟分析。在地表运动物质冲击压力计算方面,Armanini(1997)提出泥石流冲击压力由动压力和平均静止压力两部分组成,获得了广泛应用。Ceccato et al.(2017)在物质点法的框架下,基于线性脉冲原理(Jóhannesson et al.,2009),提出了土质滑坡冲击压力的计算公式。Li et al.(2018)通过建立物质点法刚柔接触模型,分析了泥石流沿山坡流下冲击挡土墙的理想情况。Feng et al.(2019)采用耦合SPH和FEM模拟了深圳滑坡的三维运动过程和对建筑物的冲击作用。
滑坡灾害的风险评价需要了解滑坡从稳定、失稳到运动、冲击和停积的全过程状态和特征。现有滑坡数值模拟研究大多关注滑坡的失稳和运动过程,或假定失稳条件下进行滑坡运动和冲击特征数值模拟研究。同时,这些研究多以特殊的滑坡几何模型为基础,其工程适用性尚不明确。本文拟在物质点法(MPM)框架下对深圳滑坡失稳、运动和冲击特征开展数值模拟,并与实际观察到的滑坡滑面、运动及堆积特征进行逐一对比,提供一套再现滑坡稳定—失稳—运动—冲击—停积全生命周期的数值模拟方法,从而为单体滑坡风险定量评估提供物理力学模型基础。
1 物质点法基本理论
1.1 物质点法基本原理
物质点法结合拉格朗日法和欧拉法的双重优势,将连续体材料离散为一系列带有质量、应变等所有信息的物质点。背景网格不携带材料信息,仅用于求解控制方程。如图1(Soga et al.,2016)所示,在每一个时间步中,物质点的所有信息通过形函数映射给背景网格结点,求解后,网格结点又将所有计算后的信息映射回各物质点,从而得到这些物质点在下一个时刻的初始信息。在每个时间步结束后,物质点法会丢弃掉畸形网格,因而在模拟大变形上具有显著优势。
1.2 物质点法控制方程及弱形式
1.2.1 更新拉格朗日型控制方程
(1)
边界条件:
(2)
初始条件:
ui(X,0)=ui0(X)
(3)
ui,t(X,0)=ui,t0(X)
(4)

1.2.2 更新拉格朗日式的弱形式
(5)

1.3 物质点离散
物质点法将材料进行离散,用物质点来代替相应的离散体,且采用背景网格进行计算。而背景网格形函数的导数在网格之间不连续,当物质点跨越背景网格时会产生数值噪声。Bardenhagen et al.(2004)提出了基于特征函数χp(x)的广义插值物质点法(generalized interpolation material point method,GIMP),从而有效降低了因物质点跨越背景网格而产生的数值噪声,进一步提高了计算精度。
χp(x)用于确定质点所占据的空间区域,χp相当于质点在空间所有质点中所占据的体积份数,故满足:
(6)
物质点的体积可以表示为:
(7)
式中:Ωp为物质点p在现时构形中的所占据的区域。

(8)
(9)
(10)
从而,可将弱形式方程(5)表示成如下形式:
(11)
利用背景网格将虚位移近似为:
(12)
将式(12)代入式(11),得到
(13)
式中:
(14)
(15)
(16)
(17)
(18)
式中:NI(x)为背景网格结点I的形函数。
1.4 本构模型
基岩采用弹性模型,土体选用Drucker-Prager屈服准则下的理想弹塑性模型。在弹性阶段,应力-应变关系为线性,即:
σij=λεkkδij+2μεij
(19)
式中:εkk为体积应变;δij为柯式δ(Kronecher-δ);εij为应变张量;λ、μ为拉梅常数。弹性模量E、泊松比v满足:
(20)
(21)
在剪切方向上,采用Drucker-Prager屈服面,即:
(22)
式中:J2为偏应力张量的第二不变量;qφ为摩擦系数;I1为应力张量的第一不变量;kc为纯剪切状态时的屈服应力。材料常数qφ和kc与内摩擦角φ和黏聚力c的关系为:
(23)
(24)
2 深圳滑坡物质点法模型构建
2.1 滑坡基本概况
2015年12月20日深圳光明新区发生特大滑坡,摧毁33栋建筑物,共造成77人死亡和失踪。滑坡主滑方向N20°W,运动距离为1100im。滑坡平面图如图2所示。深圳滑坡主要由底部花岗岩基岩和上部人工堆填体组成。其中堆填体可细分为第一层建筑渣土和第二层采石场弃土。图3为深圳滑坡A-A′剖面图(Yin et al.,2016),滑坡整体堆积较缓,堆积坡角为6.1°。滑坡堆积区最大堆积厚度为21.3im,平均堆积厚度为12.9im。从图3中可以看出在滑坡堆积区范围内存在建筑物1#~4#,本文将以这4排建筑物所处的位置,进行滑坡运动物质冲击压力和冲击荷载计算。
2.2 物质点法模型构建
2.2.1 物质点模型
本文基于MATLAB开发了物质点法的前处理程序。背景计算网格采用八节点六面体单元,每个网格含有8个物质点,网格尺寸为2im,物质点间距为1im。总计生成物质点127i118个,其中72i996个物质点代表基岩(图4中蓝色点),54i122个物质点代表土体(图4中红色点)。
2.2.2 计算参数
模型计算参数的取值采用Yin et al.(2016)对深圳滑坡开展的环剪试验结果,如表1(Yin et al.,2016)所示。根据有效应力原理:
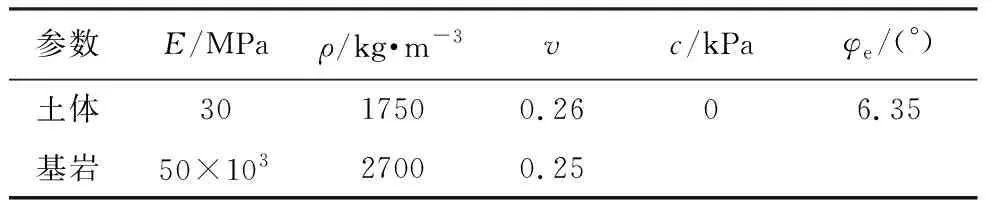
表1 深圳滑坡物质点法输入参数(Yin et al.,2016)Table 1 Parameters used in MPM(Yin et al.,2016)
τ=c′+(σ-u)tanφ′
(25)
式中:σ为总应力;u为孔隙水压力;c′为有效黏聚力;φ′为有效内摩擦角。土体采用理想弹塑性模型,故峰值抗剪强度与残余抗剪强度取值相同。因此,c′和φ′取Yin et al.(2016)环剪试验结果0ikPa和24°。
考虑地下水的作用,将孔隙水压力系数表示为:
ru=u/σ
(26)
那么式(25)可改写为:
τ=0+σ(1-ru)tanφ′
(27)
采用高杨(2018)给出的深圳滑坡孔隙水压力系数ru=0.75。按照式(28),对φ′进行等效替换(Hungr et al.,2009),得到等效内摩擦角φe。
τ=σ(1-ru)tanφ′=σtanφe
(28)
3 深圳滑坡模拟结果分析
核心计算程序采用开源代码MPM3D-F90(张雄等,2013)。首先采用动态松弛技术(Oakley et al.,1995)生成边坡初始应力场,时间为10is。在物质点法中,重力在初始时刻加载,会产生动力响应,故而需要在边坡中生成初始应力场,以满足静力平衡。在初始应力场的基础上,修改土体黏聚力c为0(孙玉进等,2015),进行深圳滑坡动力学模拟,动力计算总时间为70is,时间步长为0.849×10-4s。
3.1 滑面识别
采用经典的K均值聚类算法(Huang et al.,2013)进行滑面识别。对于一组观察值(d1,d2,…,dN),且每个观察值都是一个m维向量,K均值聚类算法的目的就是通过不断地使方差函数(J)最小化从而将N个观察值聚成K类。
(29)
式中:ck(k=1,…K)是聚类中心。K均值聚类算法在每个迭代计算周期内分为以下两步:
将物质点的相对位移作为观察值(d1,d2,…,dN),即采用一维聚类方法,N为物质点总数。滑面提取结果如图5所示,与实际滑面对比信息见表2。
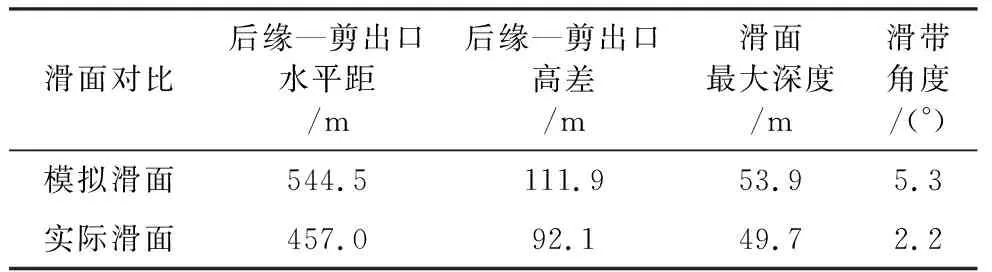
表2 模拟滑面与实际滑面对比信息一览表Table 2 Information of simulated slip surface and observed slip surface for comparison
计算结果表明,基于物质点法模拟提取的滑面与实际滑面吻合较好。模拟滑面的最大深度与实际滑面的最大深度基本一致。模拟滑面的后缘—剪出口水平距离以及高差均与实际滑面相差较小。实际滑面在中部及剪出口处均为近水平状,而模拟滑面稍有起伏。实际滑裂面后缘较陡,而模拟的滑裂面后缘较缓。值得注意的是,实际滑面是Yin et al.(2016)通过6个钻孔数据推测而来的,且相邻钻孔的最大距离达到了150im,因而实际滑面并不能完全定量反映深圳滑坡的真实情况,仅能作为参考。
3.2 滑坡运动特征分析
3.2.1 运动过程
深圳滑坡的动态数值模拟过程如图6所示。坡趾最开始产生最大剪切应变带,并不断延伸至贯通整个滑裂面(第13is左右)。其后剪出口物质点开始加速运动,进而促进滑坡整体加速运动(13~20is)。后缘物质成阶梯状不断往下溃散,经高速运动后逐渐停积并形成堆积体(20~60is)。模拟结果表明,后缘物质点运动距离较短,约为300im,中部物质点运动距离约为350im,剪出口处物质点运动距离最长,达500im。
3.2.2 运动速度
图4中特征物质点A、B、C的运动速度模拟结果如图7所示。特征物质点运动速度整体上呈现先增大后减小的趋势,不同位置的物质点运动速度差别较大。滑坡运动物质的峰值速度从前缘(物质点C)到中部(物质点B)再到后缘(物质点A)呈现递减的规律,这表明在滑坡的运动过程中,前缘的运动物质速度最快,中部的运动物质速度较快,而后缘的运动物质速度相对较慢。滑坡前缘靠近剪出口处的物质点C的速度增加最快,第20is达到最大速度16.7im·s-1。而中部物质点B出现峰值速度12.3im·s-1的时间晚于物质点C,反映了中部物质点的速度递增较慢。后缘靠近滑裂面处的物质点A的运动速度在第10is达到峰值速度7.9im·s-1之后呈现震荡变化,反映了深圳滑坡后缘物质的复杂运动特性。A点峰值速度出现的时间早于C点与B点,这表明滑坡后缘物质阶梯状溃散的快速性,同时体现了滑坡运动物质能量传递的过程。
3.3 滑坡堆积特征分析
深圳滑坡堆积特征的模拟结果如图8和表3所示。总体而言,物质点法模拟的深圳滑坡堆积形态接近实际的滑坡堆积形态。模拟的堆积坡角5.2°与实际堆积坡角6.1°基本一致。模拟的平均堆积厚度为10.3im,实际的平均堆积厚度为12.9im,两者基本吻合。模拟的最大堆积厚度(25.2im)与实际最大堆积厚度(21.3im)也基本一致。但模拟结果的运动距离(1260im)比实际运动距离(1100im)略大,主要由于本文将三维滑坡运动过程简化为二维模型,未考虑滑坡运动物质的横向扩展特征。通过与实际堆积对比,初步验证了物质点法在模拟滑坡大变形运动过程及其停积特征上的适用性。

表3 深圳滑坡模拟堆积与实际堆积对比信息一览表Table 3 Information of simulated accumulation and actual accumulation for comparison
3.4 运动物质冲击压力与冲击荷载计算
3.4.1 计算方法
Armanini(1997)认为泥石流对建(构)筑结构造成的总冲击压力理论上可表达为动压力与平均静止压力之和,其本质是将泥石流考虑为不可压缩流体,采用动量守恒定理推导而来的。本文在考虑土质滑坡失稳、运动的基础上,为建立滑坡运动物质对其运移路径上任意点的冲击压力计算理论,将滑坡运动物质考虑为不可压缩流体,采用Armanini(1997)的冲击压力(Pa)计算公式:
Pa=Pd+Ps
(30)
Pd=ρv2
(31)
Ps=0.5ρgh
(32)
式中:Pd为动压力;Ps为平均静止压力;ρ为滑坡运动物质的密度;v为冲击力作用面上的所有物质点的平均速度;h为物质点到达某点时的堆积厚度;g为重力加速度。
取单位宽度,相对应地,滑坡运动物质的总冲击荷载为冲击力与静荷载之和:
Fa=Pdh+Psh=ρhv2+0.5ρgh2
(33)
3.4.2 计算结果
针对图3所示的建筑物所处的位置1#~4#进行冲击压力的计算,结果如图9和表4所示。结果表明滑坡运动物质在点1#~4#所产生的冲击压力都表现为先快速增加至峰值再逐渐降低至稳定水平,反映了到达点1#~4#的物质点平均运动速度为先增加再递减。其中在点1#处产生的峰值冲击压力明显高于其他位置处的峰值冲击压力,这表明物质点冲击1#处的时间段正好是整个滑坡运动速度达到最大的时间段。冲击压力曲线也反映了滑坡运动物质对运移路径上某确定位置的冲击压力分为动压力和静压力,动压力占主导地位,当滑坡运动停止时,冲击压力退化为静压力。

表4 在某点处产生的冲击压力计算结果Table 4 Computed impact pressure at certain locations
峰值冲击压力随计算点与滑坡体之间距离的增加而减小。对距离滑坡后缘滑裂面最近的点1#(660im)造成的峰值冲击压力达1667.9ikPa,对距离滑坡后缘滑裂面最远的点4#(983im)造成的峰值冲击压力为490.8ikPa。根据Zanchetta et al.(2004)的研究结果,当框架结构的建筑物所受冲击压力超过100ikPa时,会遭受严重损毁。本文的计算结果在一定程度上解释了深圳滑坡导致建筑物大面积损毁和淤埋的原因。
冲击荷载的计算结果如图10和表5所示,滑坡运动物质在点1#~4#产生的冲击荷载均表现为先增加后降低至稳定水平的特点,这是由冲击压力曲线的特点决定的。在点1#处产生的峰值冲击荷载的大小是其稳定冲击荷载大小的5倍,这再次表明,冲击荷载由冲击力和静荷载两部分组成,在滑坡运动过程中,冲击荷载受运动速度的影响很大,当滑坡运动停止时,冲击荷载退化为静荷载。
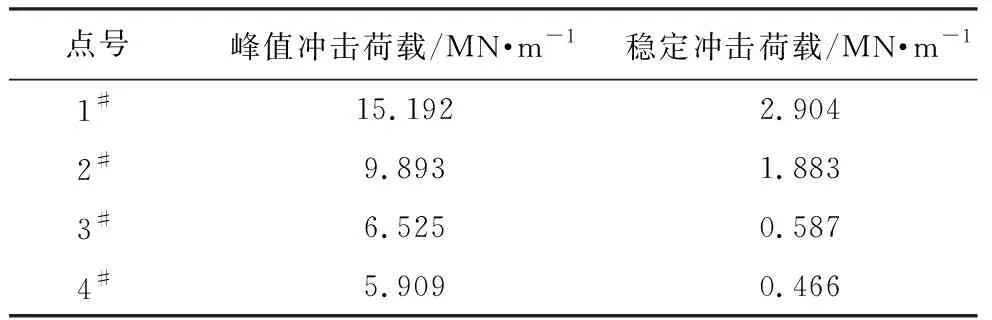
表5 在某点处产生的冲击荷载计算结果Table 5 Computed impact load at certain locations
4 结 论
本文将二维物质点法与Drucker-Prager屈服准则结合,建立了土质滑坡失稳、运动、堆积及冲击压力的数值模拟方法,并成功运用到深圳滑坡中。模拟得到了深圳滑坡的滑面、运动距离、运动速度、堆积厚度和冲击压力等关键信息。综合本文的研究,主要得出以下几点结论:
(1)物质点法不仅可以模拟滑坡运动过程与停积特征,同样可以模拟滑坡失稳过程并提取滑裂面,是再现滑坡稳定—失稳—运动—冲击—停积全生命周期的可靠数值模拟方法。
(2)采用聚类算法提取的深圳滑坡滑面与实际滑面吻合较好,验证了此类算法在基于物质点法的滑坡失稳过程数值模拟中的适用性。
(3)物质点法可再现深圳滑坡的渐进式溃散失稳特征。模拟结果显示滑坡前缘物质点运动距离最大,其运动速度明显高于中部和后缘的物质点。
(4)物质点法模拟的深圳滑坡运动距离(1260im)比实际运动距离(1100im)略大,整体堆积特征与现场实际观察结果吻合较好。
(5)计算得到的滑坡运动物质对其运移路径上4个点的冲击压力与冲击荷载整体上呈现出先快速增大至峰值,然后逐渐衰减为静压力或静荷载的特征,且峰值冲击压力与峰值冲击荷载随计算点的位置与滑坡体距离的增长而减小。该计算结果可为滑坡风险定量评估提供重要数据支撑。
