基于统一相场理论的锂电池电极颗粒断裂模拟研究1)

吴建营 洪屹峰

* (华南理工大学亚热带建筑科学国家重点实验室,广州 510641)

† (华南理工大学土木工程系,广州 510641)

引言

随着化石能源的日益枯竭,清洁可再生的新能源开发和稳定可靠的能量储存受到人们的密切关注.其中,锂离子电池由于其高容量、长循环寿命等优点被广泛应用于电子产品、电动汽车、电网等领域[1].由此,也对锂离子电池的失效分析和控制管理提出了更高的要求[2].在众多导致锂离子失效的因素中,力学行为的影响至关重要[3-4],尤其是,在充放电过程中电极颗粒表面发生锂离子的脱出或嵌入,电极颗粒材料内部发生不均匀的体积变化,从而产生拉应力并导致电极材料开裂和破坏[5-6].研究表明,电极颗粒的力学失效将会对锂离子电池的性能产生严重不利影响,具体包括: 电子电导率衰减[7]、电池容量降低[8]以及循环寿命折减[9]等.因此,研究并预测锂电池电极颗粒在充放电过程中的力学失效行为,对开发具有高能量密度、高安全性能和长循环寿命的锂电池具有重要意义.

近年来,国内外学者针对锂离子电池电极颗粒在充放电过程中的力学失效行为展开了广泛的实验和理论研究.Fincher 等[10]测试了金属锂负极材料的力学性能;Zhang 等[11]基于变分原理构建了扩散–力学耦合塑性–损伤模型,研究了将硅负极材料的力学行为.Xu 等[12]通过试验研究了无机锂盐化合物阳极材料在充放电循环过程中的力学失效行为；Klinsmann 等[13-14]等学者采用脆性断裂相场模型,研究了嵌锂和脱锂过程中化学扩散–力学变形耦合引起的阳极颗粒开裂行为;Zhang 等[15]则采用内聚裂缝模型,模拟了在充放电循环过程下电极颗粒的裂缝发展.

上述工作为研究锂电池电极颗粒的力学失效行为奠定了良好的基础.然而,遗憾的是,这些研究大多采用内聚裂缝模型或脆性断裂相场模型: 前者假定裂缝尖端的最大应力为一有限大小的材料参数(即内聚力强度或破坏强度),并采用基于强度的起裂准则描述裂缝起裂,虽然可以引入裂缝方向判据以确定裂缝扩展路径,但仍然难以考虑多裂缝、任意扩展路径等复杂行为,且数值模拟结果存在难以解决的网格敏感性问题;对于后者,无需如Griffith 线弹性力学般预设初始裂缝,且自带基于能量的裂缝扩展判据和基于系统能量最小的裂缝方向判据,代表了线弹性断裂力学的最新成果,然而其分析结果存在严重的裂缝尺度敏感性问题: 裂缝尺度越小,预测给出的峰值应力越高,因此无法完全解决裂缝起裂问题[16-17],特别是难以描述完好或仅有弱奇异性固体的裂缝演化特征.

2017 年以来,Wu[18]将断裂力学与损伤力学相结合,建立了同时适用于脆性断裂和准脆性破坏的统一相场理论.从该理论出发,不仅脆性断裂相场模型[19-20]可作为其特例直接给出,还首次提出了一类相场内聚裂缝模型即PF-CZM[21-22].作为一种裂缝正则化变分方法,相场内聚裂缝模型将基于强度的裂缝起裂准则、基于能量的裂缝扩展准则以及基于变分原理的裂缝路径判据纳入同一框架内.该模型非常便于通过有限元等方法加以数值实现,大量算例均表明其分析结果不依赖于裂缝尺度和有限元网格等数值参数,且仅需少量标准材料参数即可准确描述固体结构的损伤与破坏行为,具有十分优异的预测能力.归因于上述优点,统一相场理论和相场内聚裂缝模型一经提出,就迅速得到了国内外学者的广泛认可和直接应用[23–27].

为此,本工作拟在统一相场理论框架内,建立考虑化学扩散–力学变形耦合影响的相场内聚裂缝模型,发展相应地多场有限元数值实现算法,并应用于锂电池电极颗粒的力学失效行为研究.一方面,通过复现一些前人相关研究中的结果,验证统一相场理论扩展应用于锂电池电极颗粒开裂引发力学失效问题的适用性.另一方面,克服此前基于脆性断裂相场模型相关研究仅考虑带有初始缺陷电极颗粒的缺点,预测完好电极颗粒裂缝演化导致的力学失效.在此基础上,以期进一步发现更多潜在裂缝模式,为锂电池电极颗粒的优化设计提供科学依据.

1 化学–力学耦合相场内聚裂缝模型

不失一般性,考虑内嵌裂缝或界面的固体Ω ⊂Rndim(ndim=1,2,3),其外边界和外法向矢量分别记为 ∂Ω 和n,材料点的空间坐标记为x.对于力学场,边界 ∂Ω 划分为互补的两部分 ∂Ωu和 ∂Ωt,分别施加给定的位移边界u*(x) 和力边界t*(x) ;对于化学场,则将边界 ∂Ω 划分为 ∂ΩJ和 ∂ΩC两部分,分别施加离子通量边界J*(x) 和离子浓度边界C*(x).

虽然统一相场理论也适用于有限变形[28],这里仅考虑小应变情况,故采用位移场u(x) 和线性应变场 ε(x)=∇su(x) 描述固体的变形状态,这里 ∇s(·) 表示对称梯度算子.伴随锂电池充放电过程中电极颗粒表面锂离子的脱出或嵌入,离子浓度C(x) 发生改变,导致电极颗粒材料内部呈现不均匀的体积变化,通常采用附加化学应变 εc加以描述,并假定其大小与离子浓度变化成正比.由此,将应变张量 ε 分解为弹性应变张量 εe和化学应变张量 εc之和的形式,即

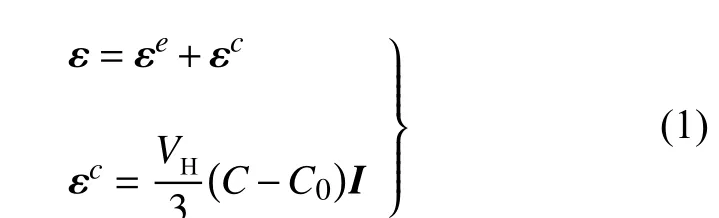
式中,VH代表锂离子的偏摩尔体积,C0为锂离子的初始浓度;I为二阶单位张量.

相场裂缝模型将尖锐裂缝/界面 S 弥散为裂缝带B ⊂Ω,其尺度记为b＞0,并引入裂缝相场d(x)∈[0,1]及其空间梯度 ∇d(x) 描述其状态.裂缝带 B 的外边界记为 ∂B,外法向矢量表示为nB.需要指出,这里裂缝带 B 并非预设或固定,而是遵循自身特定的本构关系发生起裂、扩展和演化等过程.类似地,裂缝相场也可以施加某种强制边界条件.例如,对于弹性区域有d(x)=0,对于初始裂缝有d(x)=1 等.

1.1 扩散–变形耦合过程的控制方程

对于电极颗粒表面锂离子脱出或嵌入引起的化学扩散–力学变形过程,其虚功原理表示为

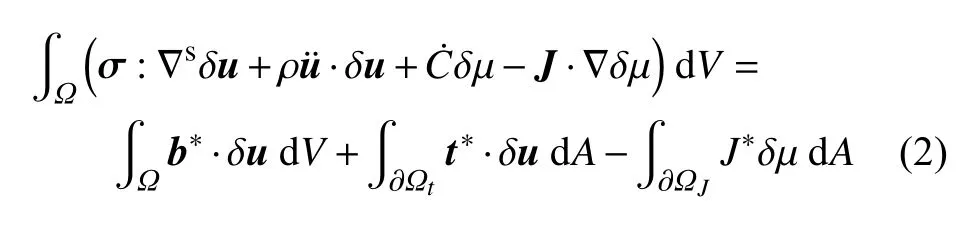
式中,b*为均布体积力,ρ 和分别为材料密度和位移加速度;J为离子通量,μ 为描述离子扩散的化学势.利用高斯–斯托克斯散度定理,可以给出

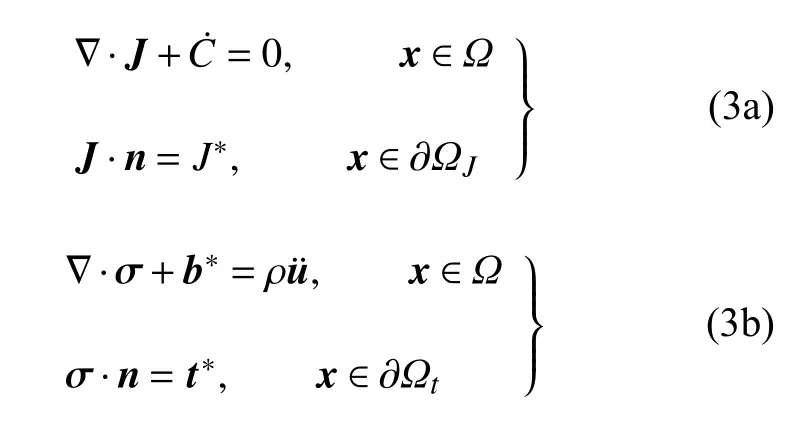
上述离子浓度和位移子问题相互耦合,共同构成化学扩散–力学变形过程的控制方程.

同时,若忽略上述耦合过程中的温度变化(即恒温假定)并考虑控制方程(3),热力学第二定律表示为如下Clausius–Duhem 不等式

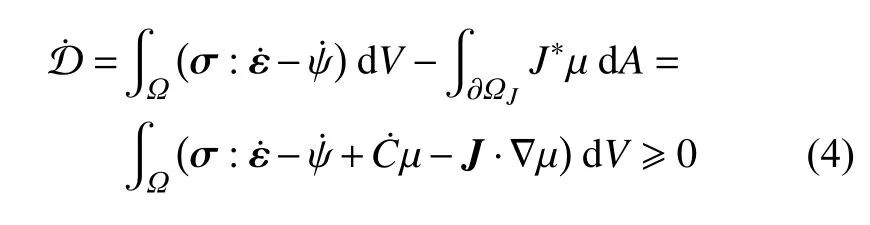
这里 ψ(ε,C,d) 为固体的Helmholtz 自由能势.由此,可以给出如下一般形式的化学和力学本构关系

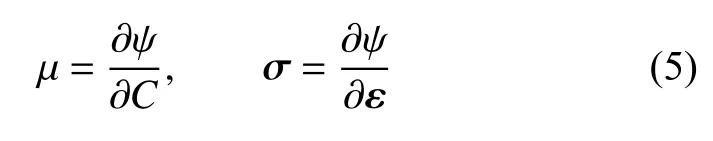
相应地,能量耗散不等式退化为

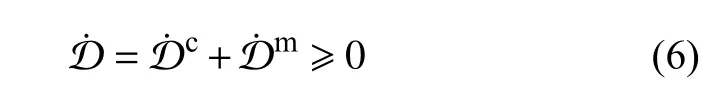
式中,化学耗散 D˙c和力学耗散 D˙m分别表示为

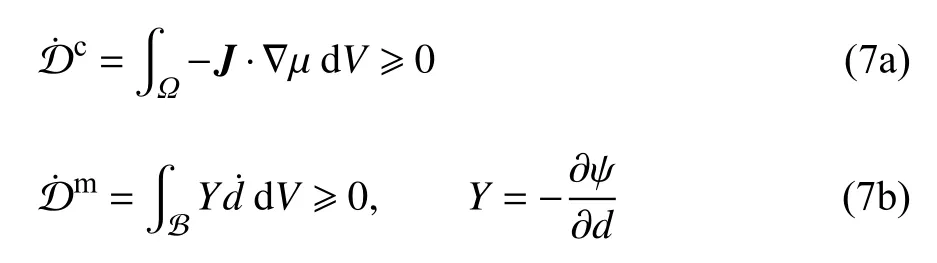
这里假设化学耗散和力学耗散相互解耦且均为非负值,以保证在纯化学扩散或纯力学变形情况下能量耗散不等式均得到满足.

离子通量J由修正的菲克定律给出[29-30]

这里,M(C) 为离子迁移率,D为扩散系数,C˜=C/Cmax为归一化离子浓度,Cmax为电极颗粒能容纳的锂离子最大浓度;R为理想气体常数,T为绝对温度.可以看出,上述离子通量自动满足化学耗散不等式(7a).

1.2 裂缝相场演化的能量原理

根据图像分割理论[31],尖锐裂缝的面积AS可以表示为如下体积分形式[32]

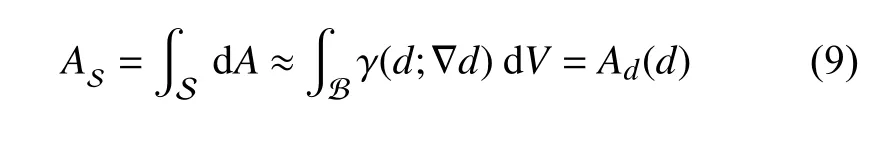
式中,裂缝面积密度函数 γ(d;∇d) 表示为[18]

这里,裂缝几何函数 α(d)∈[0,1] 是裂缝相场d(x) 的递增函数.可以严格证明: 当相场尺度参数b趋近于零时,式(9)给出的Ad(d) 收敛于尖锐裂缝的面积AS.

统一相场理论中,裂缝相场演化遵循如下能量准则[18,21]

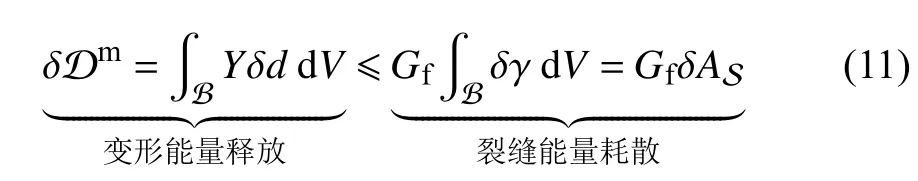
这里,材料断裂能常数Gf表征单位面积裂缝扩展所需的能量.从上式出发并结合高斯–斯托克斯散度定理,可以得到(具体推导过程详见文献[33]第1.2 节)

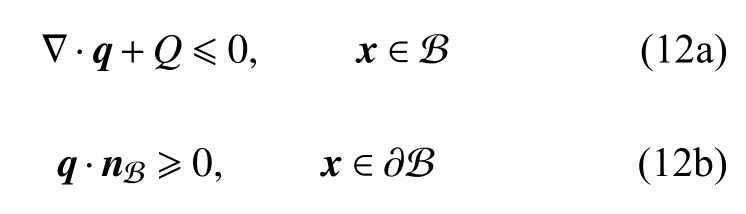
式中,热力学广义力q和源项Q分别表示为

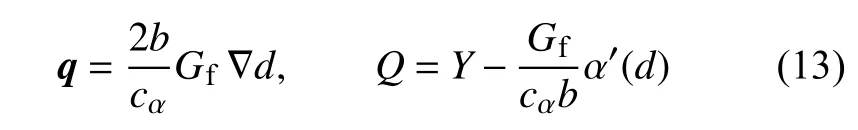
式(12)和式(13)构成了裂缝相场演化的控制方程[18,33].

1.3 化学–力学耦合本构关系

类似于应变分解式 (1),锂电池充放电过程中电极颗粒材料的化学–力学耦合Helmholtz 自由能函数可以表示为

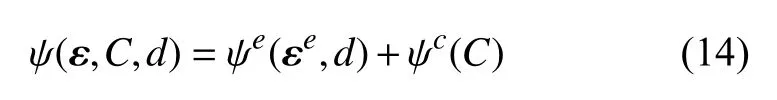
弹性势能 ψe和化学势能 ψc分别定义为

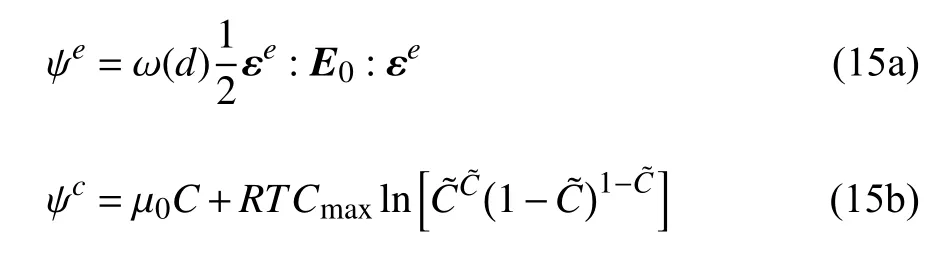
其中,E0为材料弹性刚度张量; ω(d)∈[0,1] 为单调递减的能量退化函数,表征裂缝演化对弹性应变能的影响[18]; μ0为电极材料的初始参考化学势.需要说明的是,式(15 a)假定弹性刚度张量E0与锂离子浓度C无关;如有必要,可以考虑锂离子浓度C对弹性模量等材料力学参数的影响.

相应地,由式(5)和式(8)给出化学扩散和力学变形过程的本构关系如下

上述力学本构关系式(16b)和式(17)给出的材料受拉和受压行为完全对称,这与脆性断裂和准脆性破坏的特征不符.解决这一问题最简单的策略是引入等效应力将能量释放率式(17b)重新定义为

这里,E0为材料弹性模量;是能量释放率的初始阈值,与材料破坏强度ft有关;MacAuley 括号定义为 〈x〉=max(x,0).对于脆性断裂和准脆性破坏,等效应力可取为有效应力张量的最大特征值

另一方面,由于裂缝扩展的不可逆特性,相场演化控制方程(12)为不等式.处理这一问题最简单的方法是考虑加载历史的影响,将式(13)中的裂缝相场源Q修改为

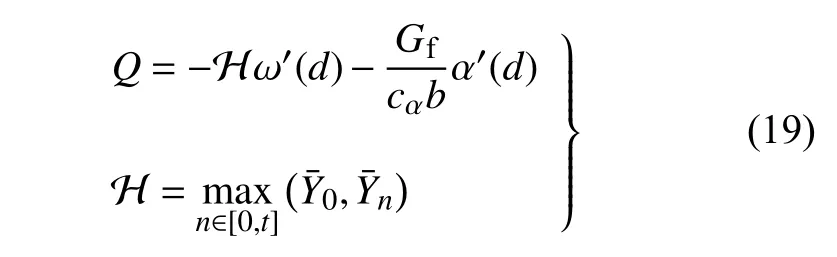
需要说明的是,对于裂缝高速动态扩展问题,可以通过哈密顿原理在裂缝相场控制方程(12a)中引入与裂缝相场一阶时间导数(裂缝扩展速率)有关的微阻尼或(和)与裂缝相场二阶时间导数(裂缝扩展加速度)有关的微惯性,以描述裂缝高速动态扩展时的能量耗散和应变率效应,具体参见前期相关工作[34].对于锂电池充放电过程脱嵌锂引起的电极颗粒开裂问题,其应变率效应很小、也很难量化,因此这里忽略裂缝相场的时间导数,仅考虑与位移速度有关的宏观惯性.然而,这并非意味着锂离子扩散和裂缝扩展相互解耦.事实上,相场控制方程中,裂缝驱动力(为弹性应变的函数)与锂离子浓度有关,而后者则与时间有关,自然考虑了锂离子扩散对裂缝扩展的时间效应;反之,虽然裂缝扩展在极短时间内完成,但裂缝相场也会直接通过裂缝尖端的静水应力对锂离子扩散产生影响.因此,如图1 所示,这里提出的模型考虑了离子扩散过程和裂缝演化过程的双向耦合.

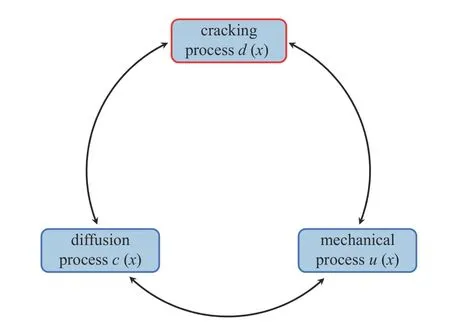
图1 锂电池电极颗粒的扩散-开裂-变形耦合过程Fig.1 Chemo-mechanical coupling in storage particles of LIBs

1.4 脆性断裂的本构特征函数

已有研究表明[18,22]: 对于脆性破坏,统一相场理论可以采用如下裂缝几何函数和能量退化函数

其中参数a1=4lch/(πb),这里Irwin 特征长度lch:=表征材料脆性程度: 其值越小,材料越脆.

如图2 所示,上述本构特征函数将给出具有线性软化曲线的相场内聚裂缝模型[21],可用于描述脆性材料的损伤破坏过程.

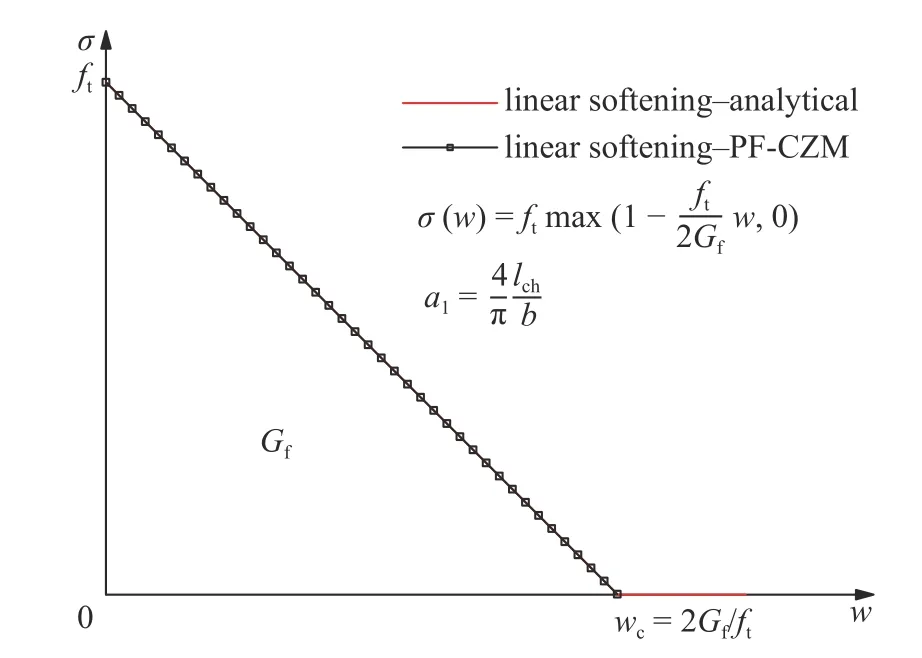
图2 具有线性软化曲线的相场内聚裂缝模型Fig.2 Phase-field cohesive zone model with a linear softening law

2 数值实现和求解算法

偏微分方程(3)和(12)构成了如图1 所示的扩散–变形–开裂过程的耦合控制方程,通常采用多场有限元方法加以求解.

2.1 控制方程的弱形式

为便于有限元数值实现,将上述偏微分控制方程转化为如下弱形式

式中,δu,δC和 δd分别为任意容许的节点位移、离子浓度和裂缝相场(变分);外力虚功和外边界离子通量虚功分别表示为

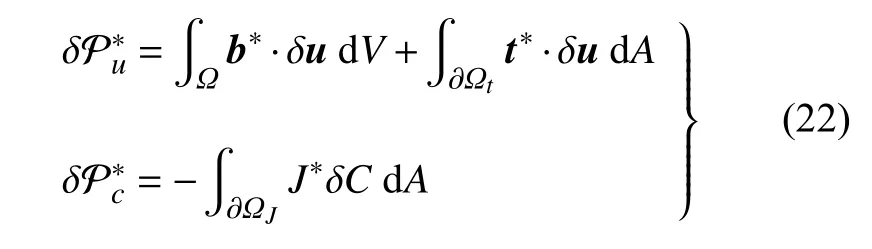
需要说明的是,这里采用式(19)给出的裂缝相场源项,故控制方程(12)及其弱形式(21)为等式.

2.2 多场有限元数值实现

有限元空间离散时,可将整个区域内所有单元节点均赋予位移、浓度和裂缝相场自由度;为了减少计算量,也可将计算域 Ω 预先划分为两部分[35]: 可能出现裂缝的子区域 B 和剩余弹性部分 ΩB.对于前者,单元节点同时具有位移、浓度和裂缝相场自由度;而后者仅赋予位移和浓度自由度.已有研究表明[18,21-22,36-37],为保证计算精度,相场子区域 B 内的单元大小一般取h≤b/5.

有限元空间离散后,位移、浓度和裂缝相场及其空间(对称)梯度分别表示为(数值实现中,所有张量均采用Voigt 标记)

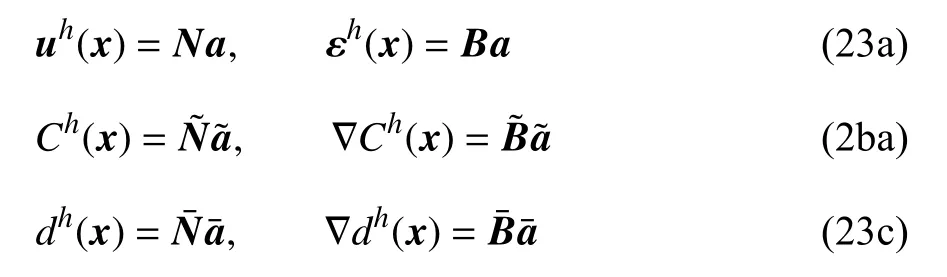
于是,由弱形式 (21)可以给出如下残量形式的平衡方程

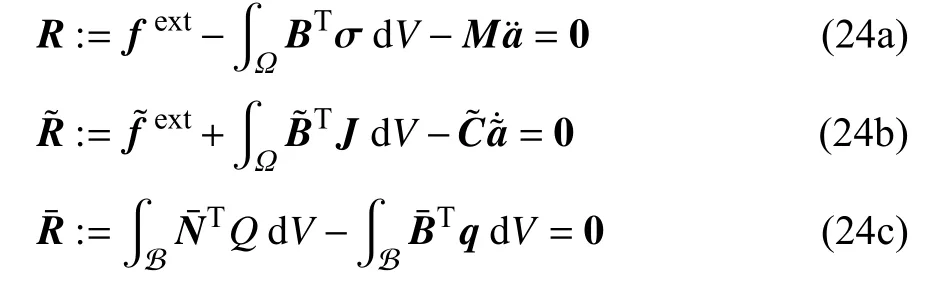
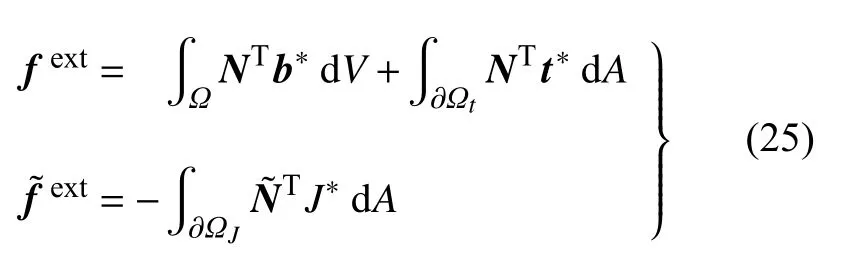
需要指出,式(16 a)中的离子通量J涉及静水应力梯度 ∇σH,在式(24b)数值实现时需要将单元积分点处的静水应力映射至单元节点,具体详见文献[38].

2.3 时间域离散

方程组 (24)通常采用增量迭代法进行求解,即将时间步 [0,t] 离散为N个增量步这里n=0,1,2,···,N-1.对于时间增量为Δt=tn+1-tn的典型子步在tn时刻所有状态变量已知的条件下,求解tn+1时刻的状态变量.

对于节点扩散速率列向量a˙˜,采用无条件稳定的向后欧拉方法进行时间域的离散,即

由此,将式 (24b)改写为

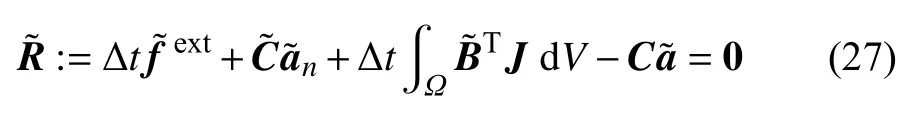
这里(下同)忽略了tn+1时刻物理量的下标n+1.

节点位移a和速度a˙ 通常由Newmark 方法[39]给出

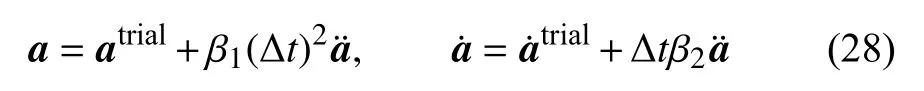
其中,节点试算位移atrial和试算速度a˙trial表示为

这里,系数 β1∈[0,0.5] 和 β2∈[0,1] 对应特定的时间积分方法.例如,β1=1/4 和β2=1/2 对应隐式中点(梯形)方法; β1=0 和 β2=1/2 对应显式中心差分方法.

后续数值模拟均采用隐式Newmark 方法即 β1≠0.此时,式(24a)可表示为节点位移an+1的残量方程

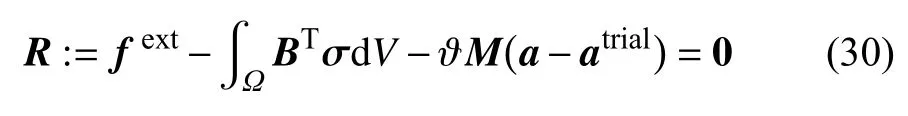
2.4 交错迭代算法

式(24c)、式(27)和式(30)共同构成了以节点裂缝相场、浓度和位移a为未知量的非线性代数方程组,通常采用迭代方法进行求解.为了保证数值求解的健壮性,这里采用如图3 所示的交错迭代算法.

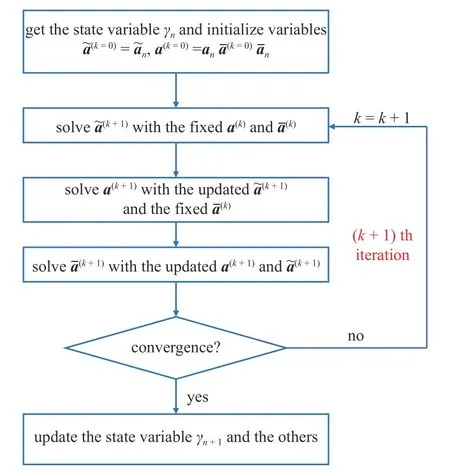
图3 求解浓度–相场–位移耦合控制方程的交错迭代算法流程图Fig.3 Flow chart of the staggered algorithm in solving the coupled governing equations

(2)根据式(30)迭代求解节点位移a(k+1),此时节点浓度固定为更新后的结果而节点裂缝相场仍然取为上一迭代步给出的结果

(3) 基于更新后的节点位移a(k+1)和浓度由式(24c)迭代求解节点裂缝相场

当控制方程的残量范数小于某一给定容差,判断为结果收敛;否则,继续重复上述求解过程直至最终收敛.

已有数值计算经验表明[18,21,33],上述交错迭代算法的收敛速度较慢,但数值健壮性极好,对于求解裂缝快速扩展引起的脆性断裂问题十分有效.

3 电极颗粒力学失效分析应用

上述化学-力学耦合相场内聚裂缝模型适用于锂电池充电(锂离子脱出)、放电(锂离子嵌入)过程中扩散应力引起的电极颗粒裂缝演化分析.由于篇幅受限,这里仅讨论锂离子脱出过程,锂离子嵌入导致的电极颗粒力学失效分析将另文给出.

研究对象为锰酸锂(LiMn2O4)锂电池阳极颗粒,材料参数如表1 所示[29,41-42,14].根据实际情况,考虑(圆或椭圆)柱体和球体两种形状的电极颗粒,分别采用二维和三维有限元进行数值分析.与已有研究[13-14]一致,化学扩散采用如下通量边界条件

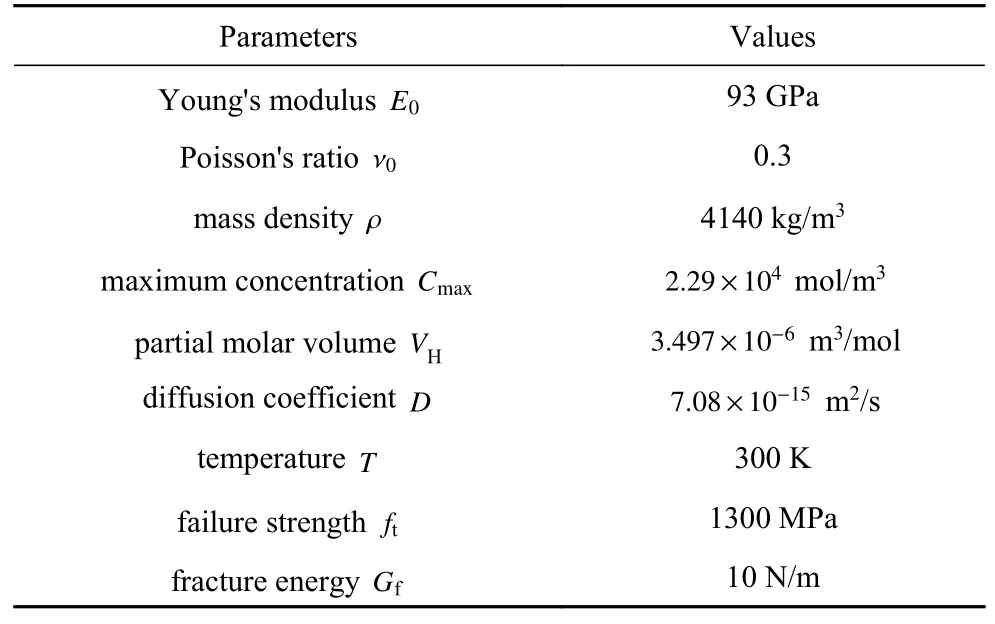
表1 锰酸锂正极颗粒材料参数取值Table 1 Material parameters of the storage particle.

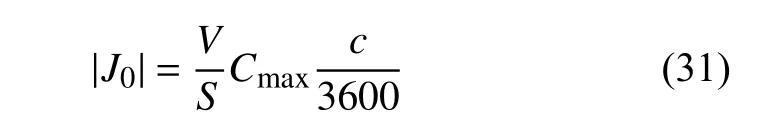
式中,c为表征锂电池充放电快慢的参数:c值越大,充放电速率越快;V和S分别表示电极颗粒的体积和表面积.锂离子脱出时,初始条件假定为C0=Cmax,边界离子浓度达到最小值0 后保持恒定.

3.1 柱体电极颗粒: 二维分析

首先考虑如图4 所示的圆形截面柱体电极颗粒,其截面半径记为r0,此时有V/S=r0/2.

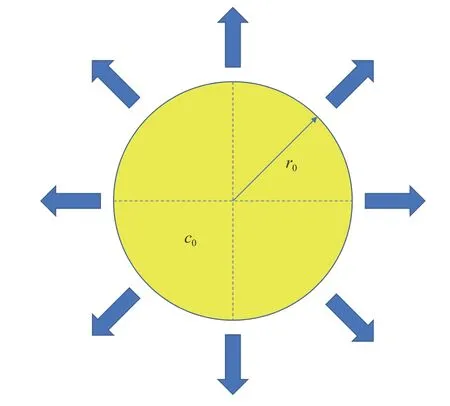
图4 二维电极颗粒的几何及边界条件Fig.4 A cylindrical storage particle: Geometry and boundary conditions

为减少计算量,仅考虑圆柱体电极颗粒的截面行为,故可简化为二维问题并假定为平面应力状态.在某些情况下,还将根据问题的对称性采用 1/2 或1/4模型进行分析.由于模型计算结果与相场尺度参数b无关,所有算例中均取为b=0.05 μm,网格划分采用四节点双线性插值单元.

充电过程中,随着锂离子逐渐脱出,电极颗粒表面浓度低于中心区域.此时,式(1)中的附加化学应变大小为负值,即电极颗粒表面发生收缩变形而产生环向拉应力,而电极颗粒内部产生环向压应力,如图5 所示.

图5 脱锂过程电极颗粒的应力状态Fig.5 The mechanical stress state in the particle during Li extraction

3.1.1 弹性分析结果

首先考虑半径为r0=5 μm 的电极颗粒,其充放电速率c=1,分析时间为t=5000 s.图6 给出了最大主应力随时间的变化曲线.

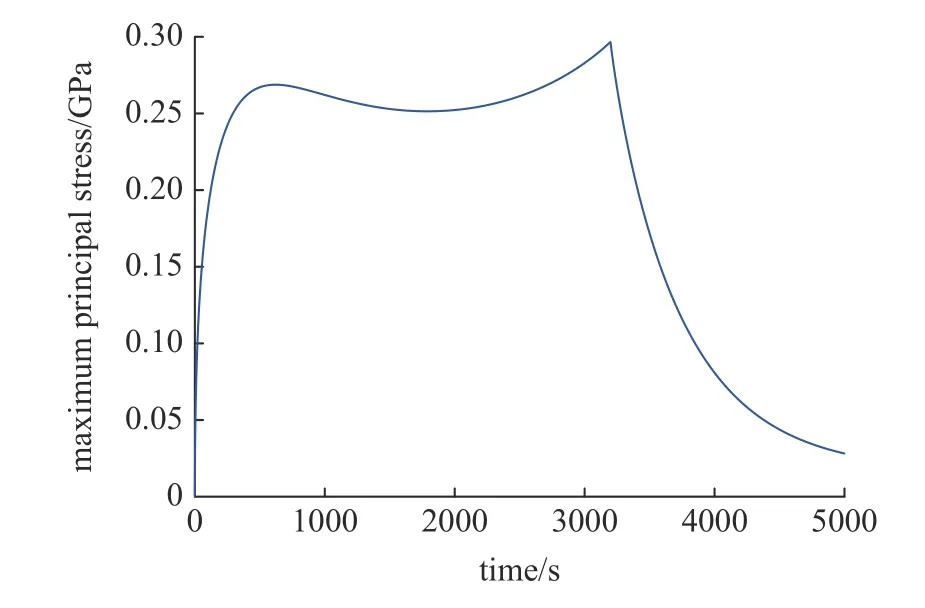
图6 电极颗粒弹性分析结果: 最大主应力随时间的变化曲线Fig.6 Elastic results of the particle: Evolution of the maximum principal stress

可以看出,上述电极颗粒的最大主应力不超过0.30 MPa,明显小于材料破坏强度ft=1.3 GPa,此时材料处于线弹性状态.

在线弹性阶段,附录给出的解析解表明,圆柱体电极颗粒静水应力的拉压分界线 σH(r)=0 与截面平均浓度等值线C(r)=重合.为了验证这一结果,图7给出了不同时刻平均浓度C=(具体数值见表2)等值线与静水压力拉压分界线 σH=0 的结果.可以发现,二者完全重合.

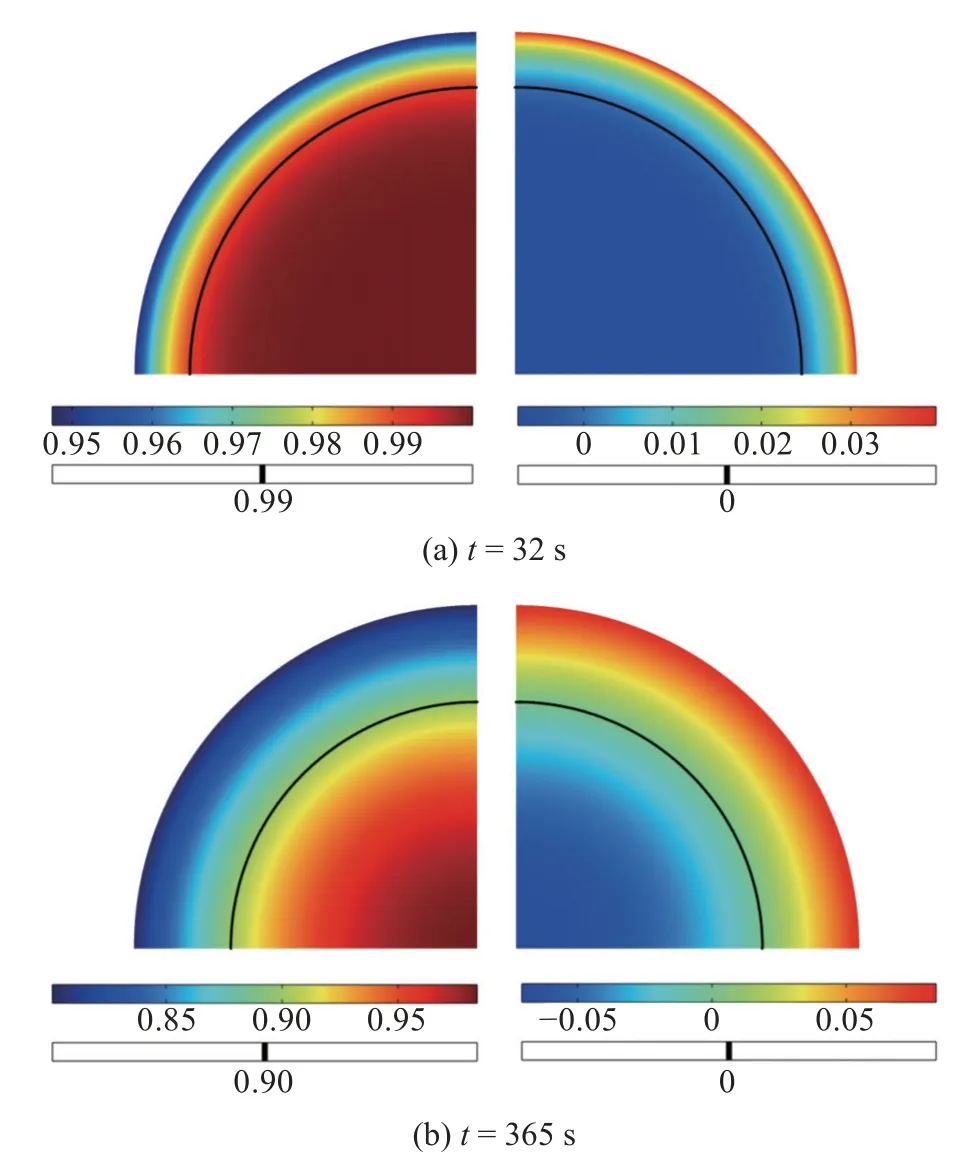
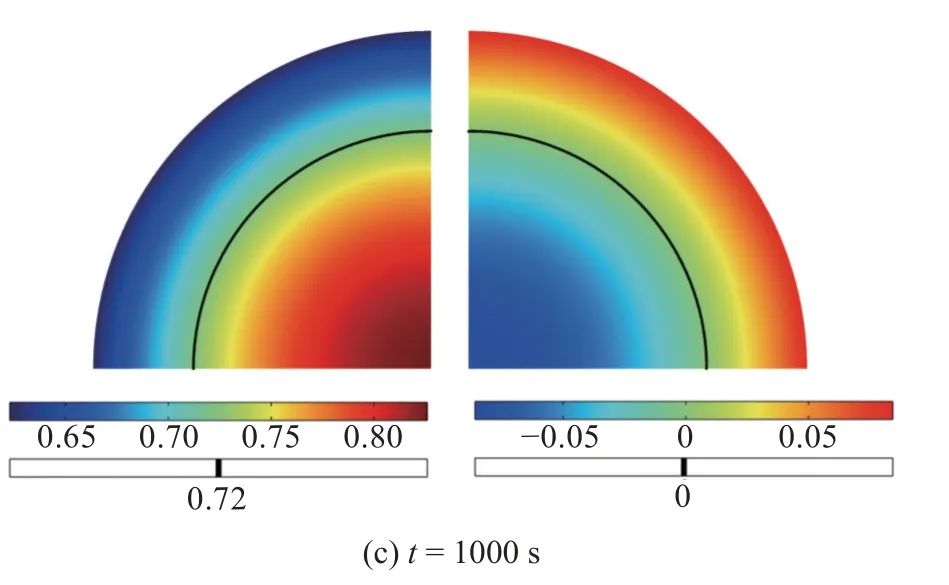
图7 电极颗粒的弹性分析结果: 静水压力(左)和平均浓度(右)等值线Fig.7 Elastic analysis results of the storage particle: Isolines of the hydrostatic stress (left) and concentration (right)

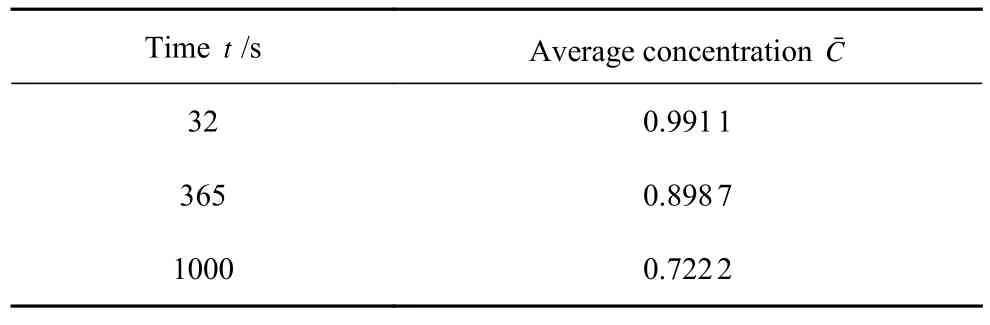
表2 不同时刻圆柱体电极颗粒的截面锂离子平均浓度Table 2 Average concentration of lithium ions in the cylindrical storage particle at various time instants

3.1.2 含初始缺陷的电极颗粒

已有研究表明[13],对于含初始裂缝的电极颗粒,其破坏模式和破坏程度受几何尺寸(如半径r0)、初始裂缝长度a0、充放电速率c和最大锂离子浓度Cmax等因素的影响.为验证化学–力学耦合相场内聚裂缝模型对于电极颗粒力学失效行为预测的适用性,这里对含初始缺陷的电极颗粒在脱锂过程中的裂缝演化过程进行分析,并考虑三种情况.

(1)初始裂缝不扩展.考虑半径为r0=3 μm 的电极颗粒,其充放电速率c=5,时间为t=1400 s.对于初始裂缝长度为a0=0.1 μm 和a0=1 μm 的两种电极颗粒,最终时刻的相场分布和锂离子浓度分析结果如图8 所示.

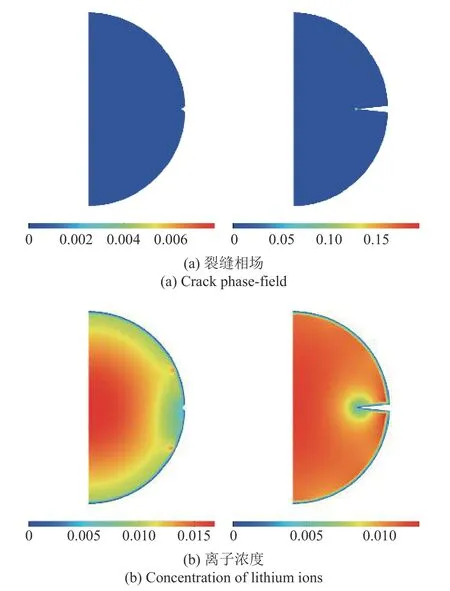
图8 含初始缺陷电极颗粒的裂缝不扩展模式: 裂缝相场和离子浓度云图(左 a0=0.1 μm,右 a0=1.0 μm)Fig.8 Pre-notched particles with no cracking growth: Profiles of the crack phase-field and concentration field (left: a0=0.1 μm,right: a0=1.0 μm)

可以看出,对于有初始裂缝的电极颗粒,虽然应力集中导致两种情况下裂缝尖端的最大主应力均超过材料破坏强度(如图9 所示),且初始裂缝长度越大应力集中越明显,但初始裂缝是否扩展由能量准则加以判断,由于两种情况下电极颗粒半径较小且充放电速率较低,直至锂离子浓度最终近乎为0,流入裂缝尖端的应变能仍然不足以驱动初始裂缝进一步扩展,可以认为此时电极颗粒处于安全状态[13].

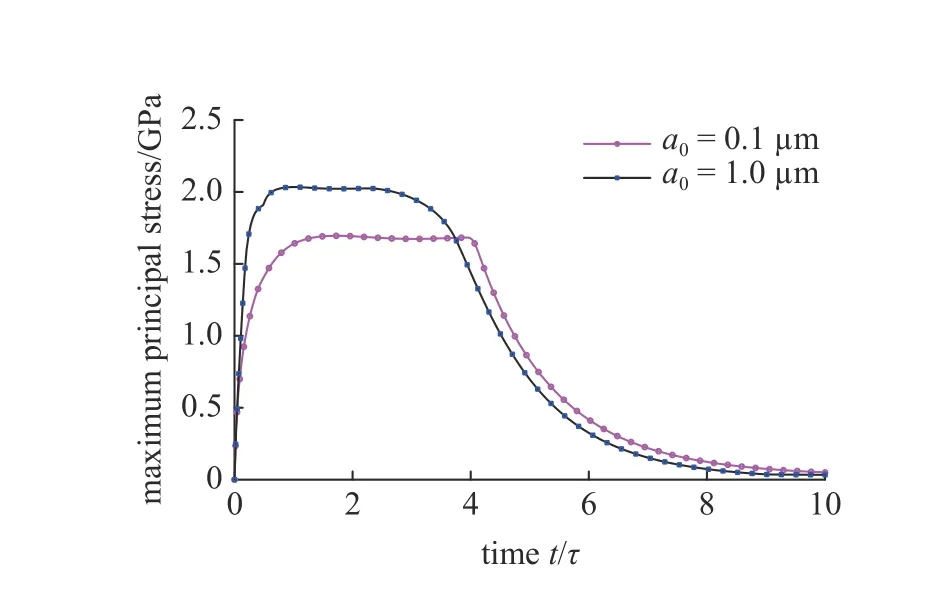
图9 含初始缺陷电极颗粒的裂缝不扩展模式: 最大主应力Fig.9 Pre-notched particles with no cracking growth: Evolution of the maximum principal stress

图10 给出了电极颗粒内部的最大浓度与最小浓度之差 ΔCmax以及平均浓度(通常被称为电极充放电状态) SOC 随时间的变化曲线.可以看出,初始缺陷长度对电极颗粒锂离子平均浓度的影响不大,但对最大浓度与最小浓度之差 ΔCmax产生明显影响.这是因为: 脱锂过程中,浓度梯度 -∇C与静水压力梯度 ∇σH的方向基本一致(如图11 所示),即静水压力对离子扩散起到正向加速的作用,且越靠近边缘处,扩散速率越大.对于a0=1 μm 的电极颗粒,其应力水平更高,电极颗粒表面处离子扩散的加速作用更加明显,由此导致了更大的内外浓度差.

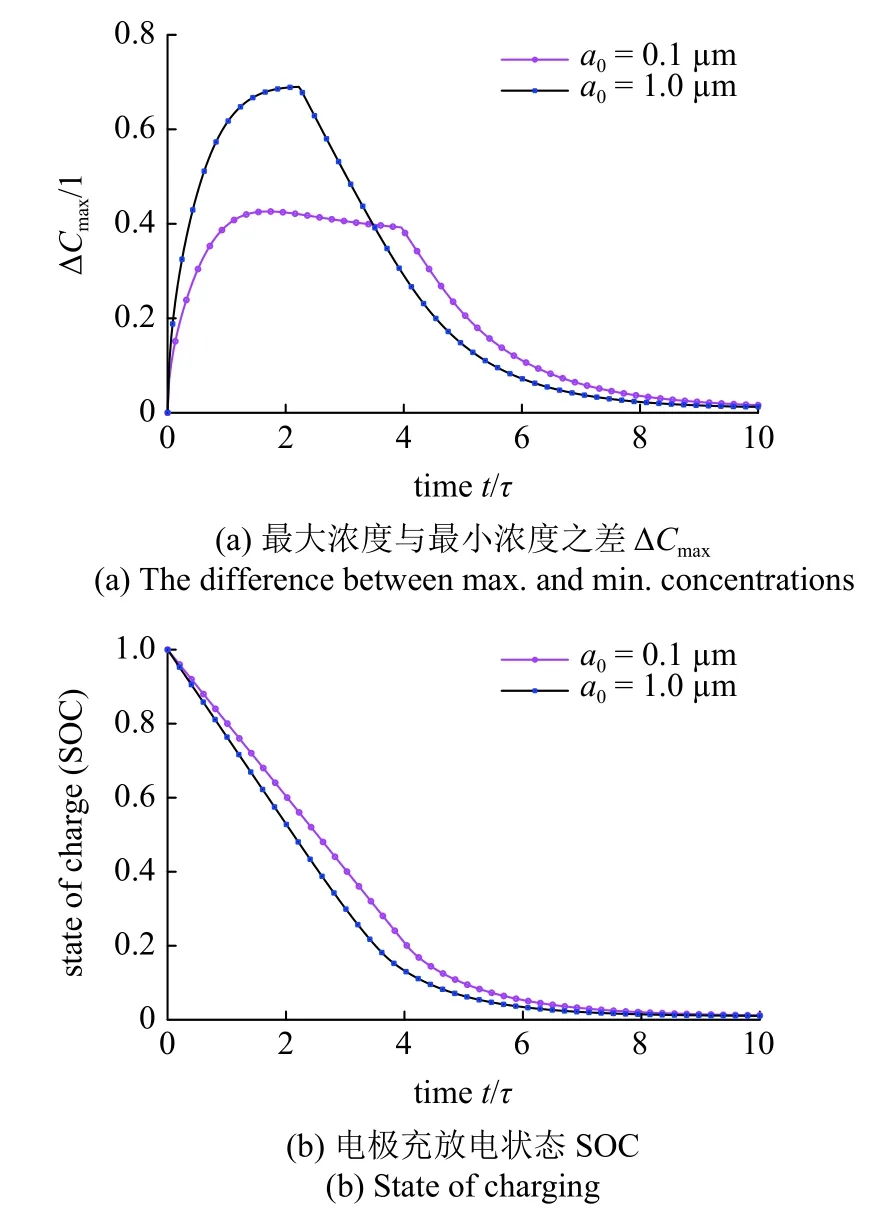
图10 含初始缺陷电极颗粒的裂缝不扩展模式Fig.10 Pre-notched particles with no cracking growth

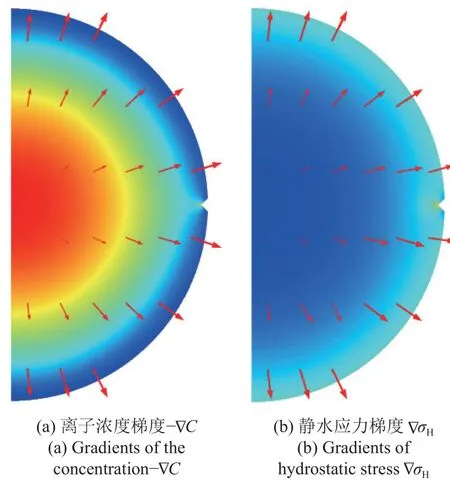
图11 含初始缺陷电极颗粒的裂缝不扩展模式Fig.11 Pre-notched particles with no cracking growth

(2)单裂缝扩展.考虑半径为r0=3 μm、初始裂缝长度a0=1 μm 的电极颗粒,充放电速率增大至c=10,时间同样为t=1400 s.数值模拟给出的裂缝演化如图12 所示.

图12 含初始缺陷电极颗粒的单裂缝扩展模式:不同时刻的裂缝相场云图Fig.12 Pre-notched storage particles with a single cracking growth:Profiles of the crack phase-field at various time instants

由通量边界条件 (31)可知: 提高边界锂离子的脱出速率会在电极颗粒表面产生更大的收缩变形和更大的环向拉应力,导致初始裂缝扩展;由于电极颗粒内部存在压应力区域,裂缝扩展将最终停止(对于本算例,裂缝扩展停止于时刻t≈177 s,最终裂缝长度(不包括初始长度)约为0.55 μm 左右).

(3)多裂缝扩展.基于前述分析可知,脱锂过程中,随着裂缝逐渐扩展,受内部压应力区影响裂缝尖端处拉应力逐渐减小直至裂缝停止发展;与此同时,由于持续发生收缩变形,电极颗粒表面拉应力不断增大.因此,可以预见: 表面拉应力增大到一定水平后,可能会在初始裂缝以外的其他位置产生多条向内发展的附加裂缝.

为了验证该推测,考虑半径为r0=10 μm、初始裂缝长度a0=1 μm 的电极颗粒,充放电速率c=10,分析时间t=50 s.数值模拟给出的裂缝演化过程如图13 所示.

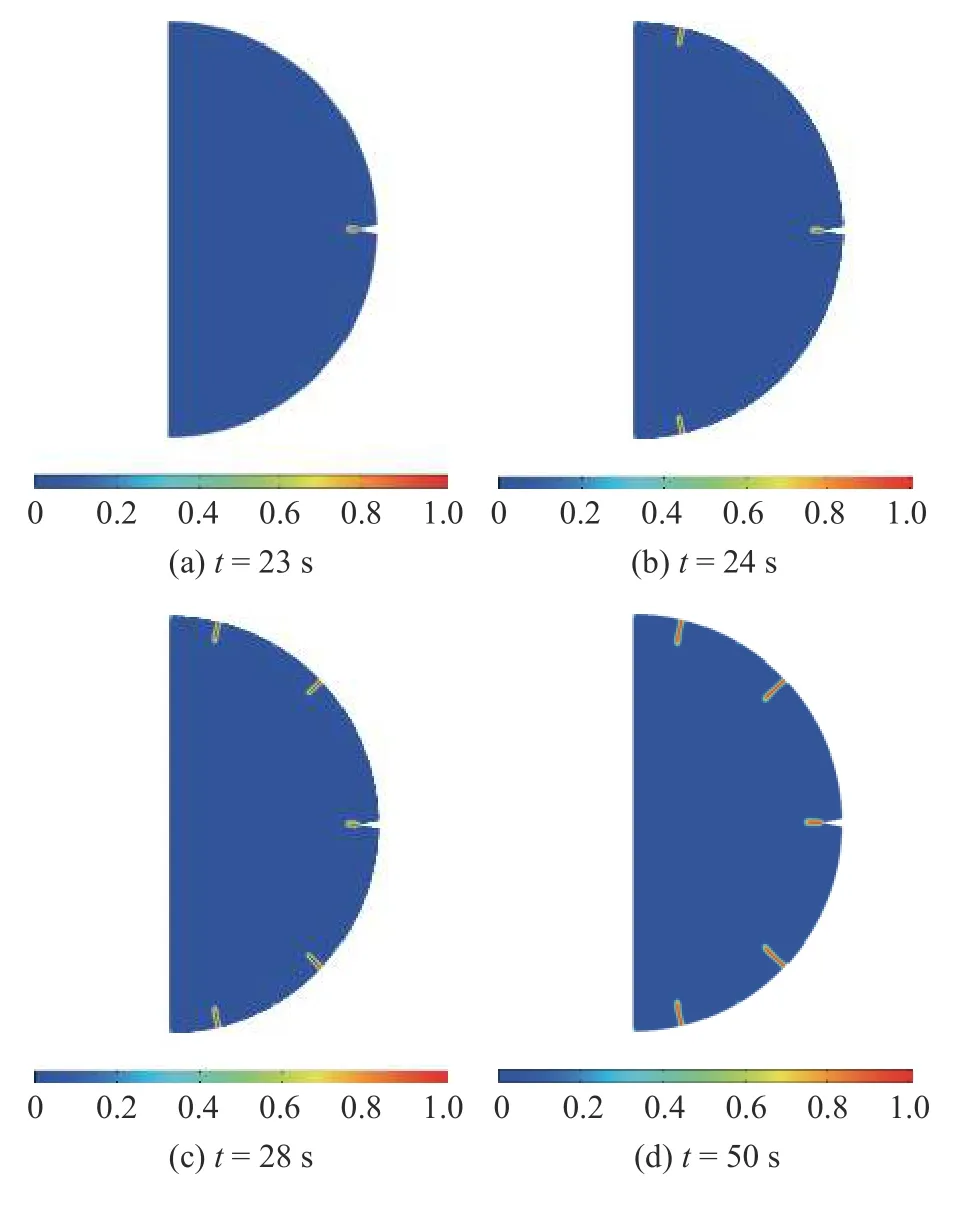
图13 含初始缺陷电极颗粒的多裂缝扩展模式:不同时刻的裂缝相场云图Fig.13 Pre-notched particles with multiple cracking growths: Profiles of the crack phase-field at various instants

可以看出,随着初始裂缝停止扩展,电极颗粒表面其他位置处出现新的附加裂缝.其原因,从如图14所示的裂缝尖端和电极颗粒表面的最大主应力随时间的变化曲线可以看出:

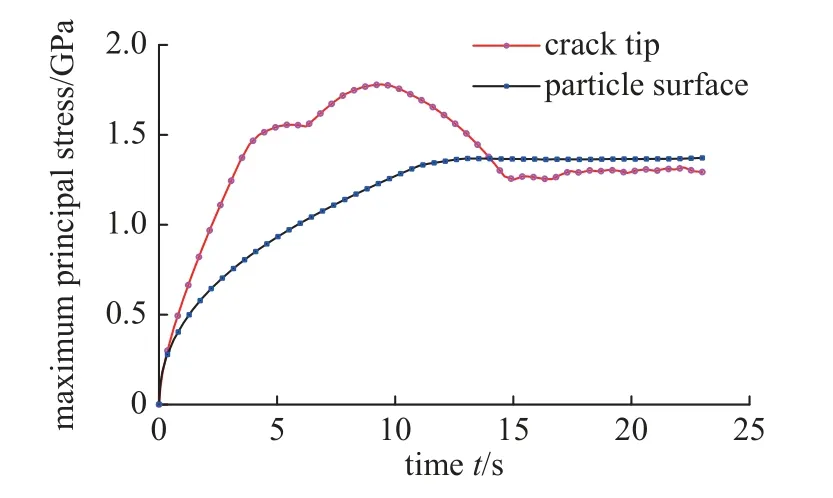
图14 含初始缺陷电极颗粒的多裂缝扩展模式: 裂缝尖端和电极表面的最大主应力随时间的变化曲线Fig.14 Pre-notched particles with multiple cracking growths: Evolution of the principal stresses at the crack tip and surface

①时间段t∈[0 s,9 s] : 初始裂缝尖端和电极颗粒表面的最大主应力均呈增长趋势,且受应力集中影响,裂缝尖端应力增长更快;

② 时间段t∈[9 s,15 s] : 初始裂缝向内部受压区发展,裂缝尖端主拉应力水平下降;与此同时,电极表面的拉应力继续缓慢增加;

③时间段t∈[15 s,23 s] : 表面锂离子浓度进一步降低,裂缝尖端的最大主应力低于材料抗拉强度ft=1.3GPa,初始裂缝停止发展;相应地,颗粒表面的主拉应力逐渐趋于恒定,但略高于材料强度,电极表面开始出现附加裂缝.

3.1.3 无初始缺陷的电极颗粒

3.1.2 节分析的电极颗粒均预设了一定长度的初始裂缝,主要考虑脱锂过程中初始裂缝是否会发生进一步扩展.本节进一步分析无初始缺陷的电极颗粒在脱锂过程中的力学失效行为.

(1)安全状态.考虑半径为r0=3 μm 的电极颗粒,充放电速率为c=60,分析时间为t=60 s.数值模拟给出的裂缝相场演化如图15 所示.

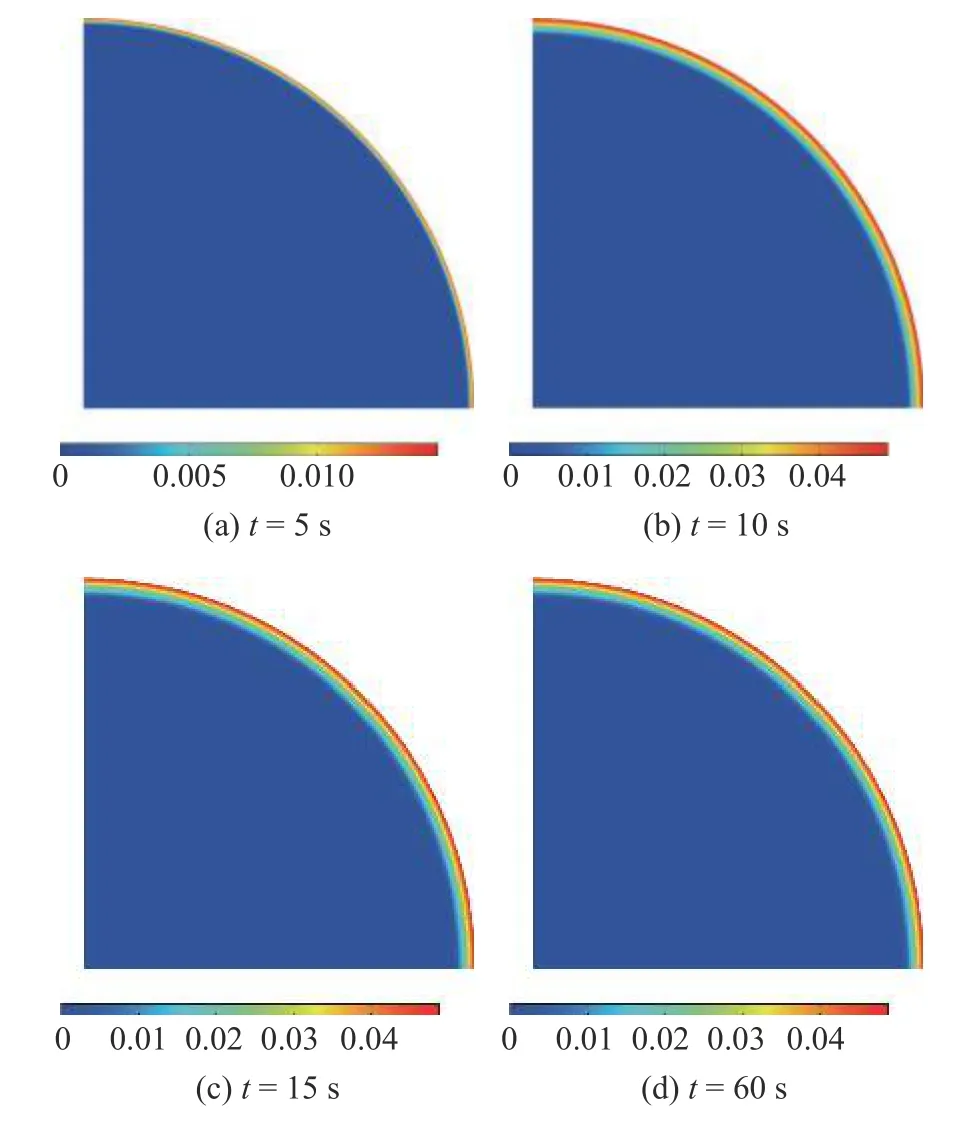
图15 无初始缺陷电极颗粒的安全模式: 裂缝相场演化云图Fig.15 Intact particles with no cracking grow: Profiles of the crack phase-field at various time instants

可以看出,尽管充放电速率c远大于同半径含初始裂缝的电极颗粒,裂缝相场在t=10 s 左右达到最大值d≈0.05 后停止增长,此时电极颗粒表面呈现均匀分布的微裂缝,未发生局部化并形成向内发展的宏观裂缝,故可认为电极颗粒处于安全状态.这也说明,初始裂缝对电极颗粒的力学失效有较大影响.

(2)多裂缝模式.由于电极颗粒表面拉应力均匀分布,可以预期: 随着电极颗粒尺寸或(和)充放电速率增大,颗粒表面将会出现多条裂缝.

为了避免对称模型对模拟结果的影响,考虑半径r0=15 μm 的完整圆形截面模型,充放电速率为c=10,分析时间为t=200 s.模拟给出的裂缝演化过程如图16 所示.

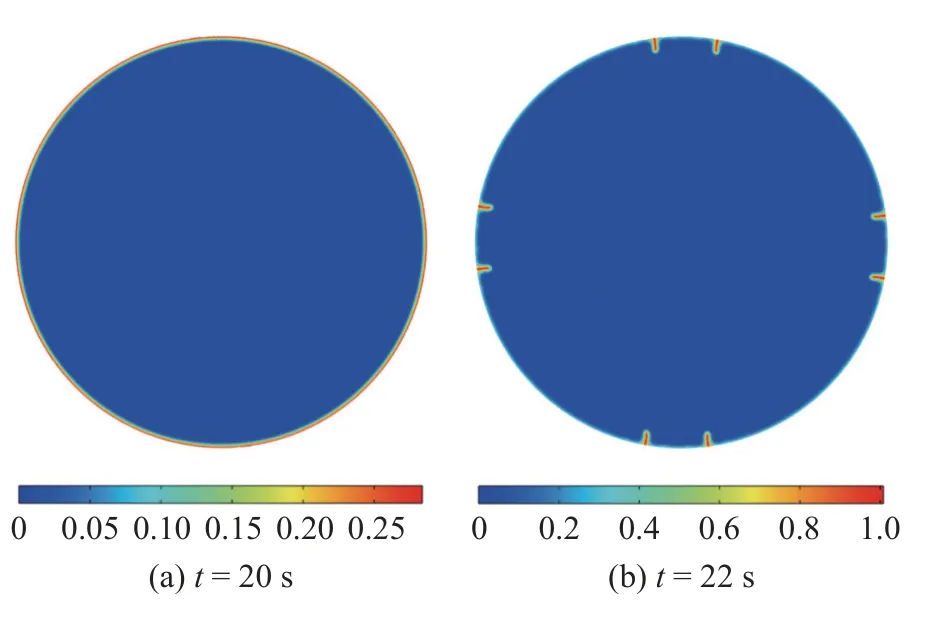
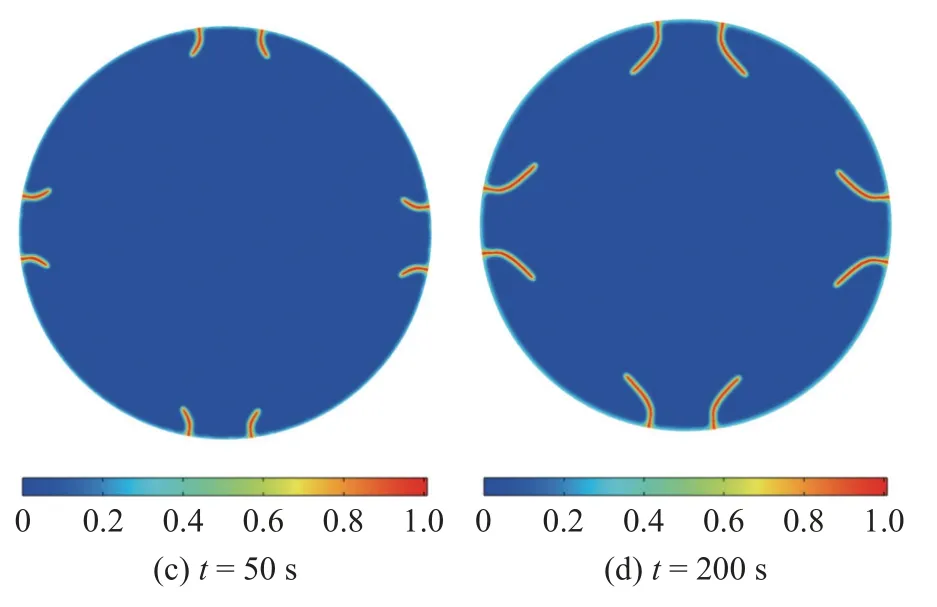
图16 无初始缺陷电极颗粒的多裂缝模式: 裂缝相场演化云图Fig.16 Intact particles with multiple cracking grows: Profiles of the crack phase-field at various time instants

从图中可以看出: 在锂离子脱出过程中,开始阶段裂缝表面均匀分布的裂缝相场出现局部化,并呈大致对称形式发展;扩展过程中,由于内部受压区的存在,裂缝会在受压区外边缘沿环向偏转.

为了进一步考虑充放电速率的影响,对同样半径的电极颗粒开展不同充放电速率下的电极颗粒破坏模式分析.数值模拟给出的最终裂缝相场分布如图17所示.

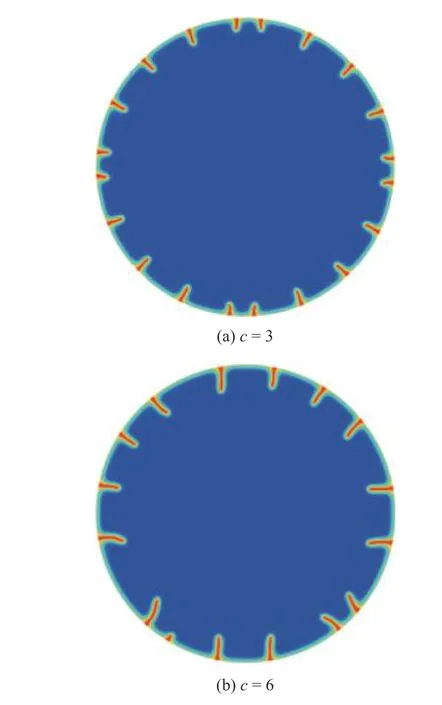
图17 无初始缺陷电极颗粒的多裂缝模式: 不同充放电速率下的最终裂缝相场云图Fig.17 Intact particles with multiple cracking grows: Profiles of the crack phase-field for various charging rates

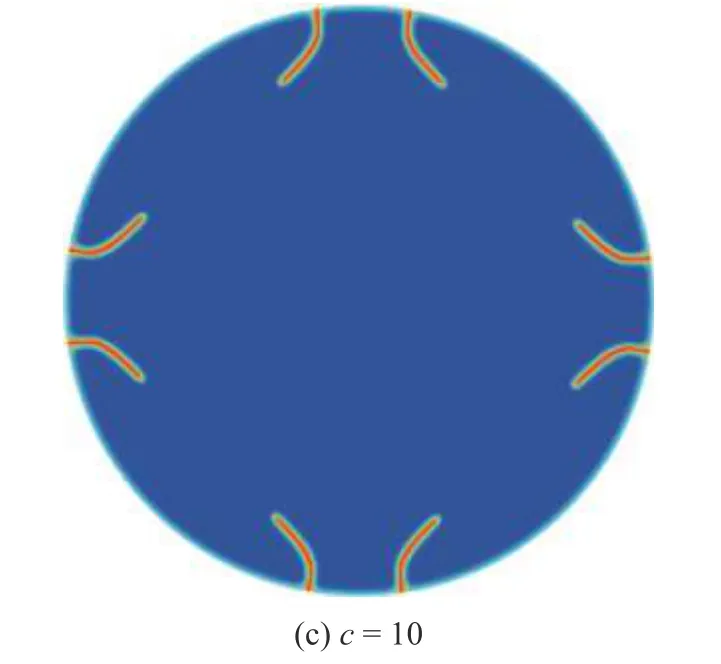
图17 无初始缺陷电极颗粒的多裂缝模式: 不同充放电速率下的最终裂缝相场云图(续)Fig.17 Intact particles with multiple cracking grows: Profiles of the crack phase-field for various charging rates (continued)

由此可见,同等尺寸下,充放电速率越小,出现的总裂缝数量越多,且每条裂缝几乎等间距均匀分布于电极颗粒表面,但其最终的裂缝发展长度较小;反之则相反.需要指出,当充放电速率较高时,每条裂缝为了达到更大的长度,裂缝受到内部压应力的阻止会沿环向偏转.

3.1.4 形状效应分析

在弹性阶段,已有解析解和数值结果表明[29,43],锂离子扩散引起的应力不仅与电极颗粒的尺寸大小和充放电速率有关,还受到其截面形状的影响: 相比截面高宽比较大(如椭圆形)的电极颗粒,高宽比较小(如圆形截面)的电极颗粒会产生更大的应力,由此可能出现更为严重的破坏.

为验证上述结论,考虑相同面积和边界锂离子流量条件下不同高宽比电极颗粒的开裂行为.模拟中,电极颗粒面积与半径r0=5 μm 的圆形电极颗粒相同,式 (31) 中的边界锂离子通量均为J0=2.1×10-4mol/(m2·s),脱锂时间设定为100 s.

数值模拟给出的最终裂缝相场云图如图18所示.

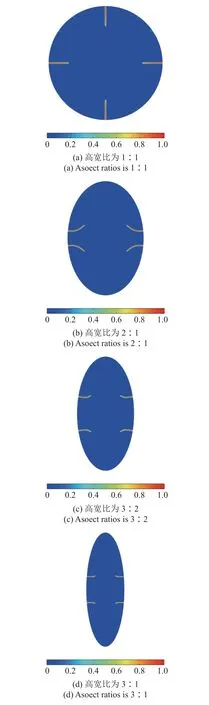
图18 截面面积相同、高宽比不同的电极颗粒: 最终裂缝相场云图Fig.18 Damage profiles in storage particles with identical section area but of various aspect ratios

相应地裂缝长度随时间发展曲线如图19 所示.可以看出,同等截面面积和锂离子边界条件下,截面高宽比小的电极颗粒更早出现了局部化裂缝,且在相同扩散时间内裂缝总长度更长,因此更容易发生、更为严重的力学失效,这与线弹性应力分析结果[29]一致.

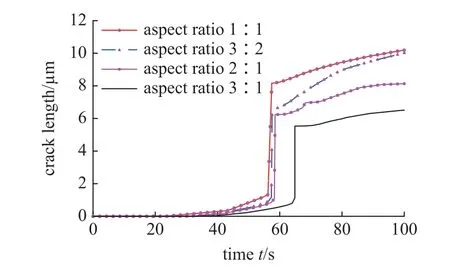
图19 截面面积相同、高宽比不同的电极颗粒: 裂缝长度演化曲线Fig.19 Crack lengths in storage particles of identical section area but of various aspect ratios

3.2 球体电极颗粒: 三维分析

接下来,考虑球体电极颗粒,其半径同样记为r0,相应有V/S=r0/3.由于必须采用三维有限元分析,计算量大大增加,这里仅给出无初始缺陷电极颗粒的分析结果.此时,可以采用 1/8 球体进行建模,网格划分采用八节点实体单元.

考虑半径r0=5 μm 的球形电极颗粒,充放电速率为c=20.脱锂过程中电极颗粒内部的锂离子浓度分布如图20 所示.与二维情况一致,锂离子浓度分布由内向外单调递减.

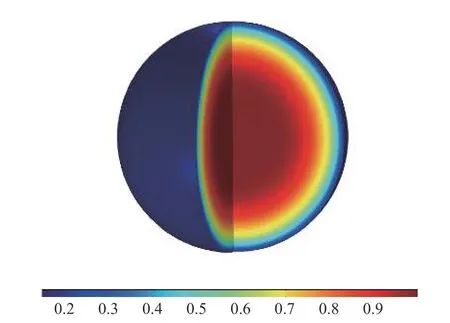
图20 球体电极颗粒三维分析: 锂离子浓度分布示意图Fig.20 Spherical storage particles: Concentration contour of Li-ion

3.2.1 弹性分析结果

在弹性阶段,电极颗粒的主应力分布及方向如图21 所示.

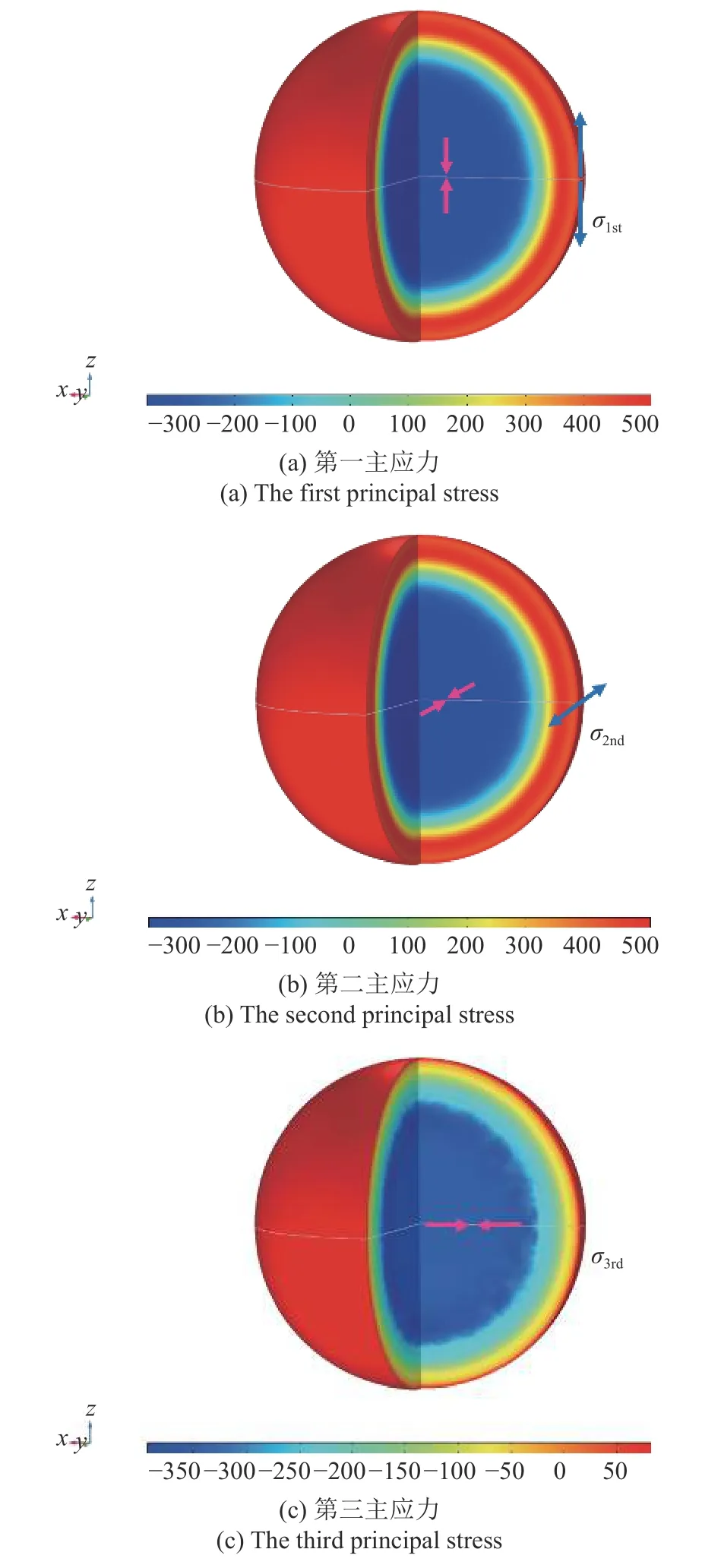
图21 球体电极颗粒三维分析: 弹性阶段的主应力云图Fig.21 Spherical storage particles: Contours of principal stresses in the elastic stage

可以看出,球体电极颗粒三维弹性分析结果与圆柱体二维分析类似,应力状态均为外部受拉、内部受压,第一、二主应力分别沿经线和纬线方向,其大小相同且大于径向的第三主应力.这一结果与附录给出的解析解一致.

3.2.2 损伤破坏全过程分析

接下来,利用相场内聚裂缝模型分析球体电极颗粒的损伤破坏全过程.由于前期大量二维和三维分析结果表明[33,44-45],相场内聚裂缝模型中尺度参数b的取值仅影响裂缝带的宽度,对破坏模式和整体计算结果几乎没有影响.因此,为减少计算量,三维分析中取用了稍大的相场尺度参数b=0.14 μm.

三维数值模拟给出的电极颗粒最终裂缝相场分布如图22 所示.

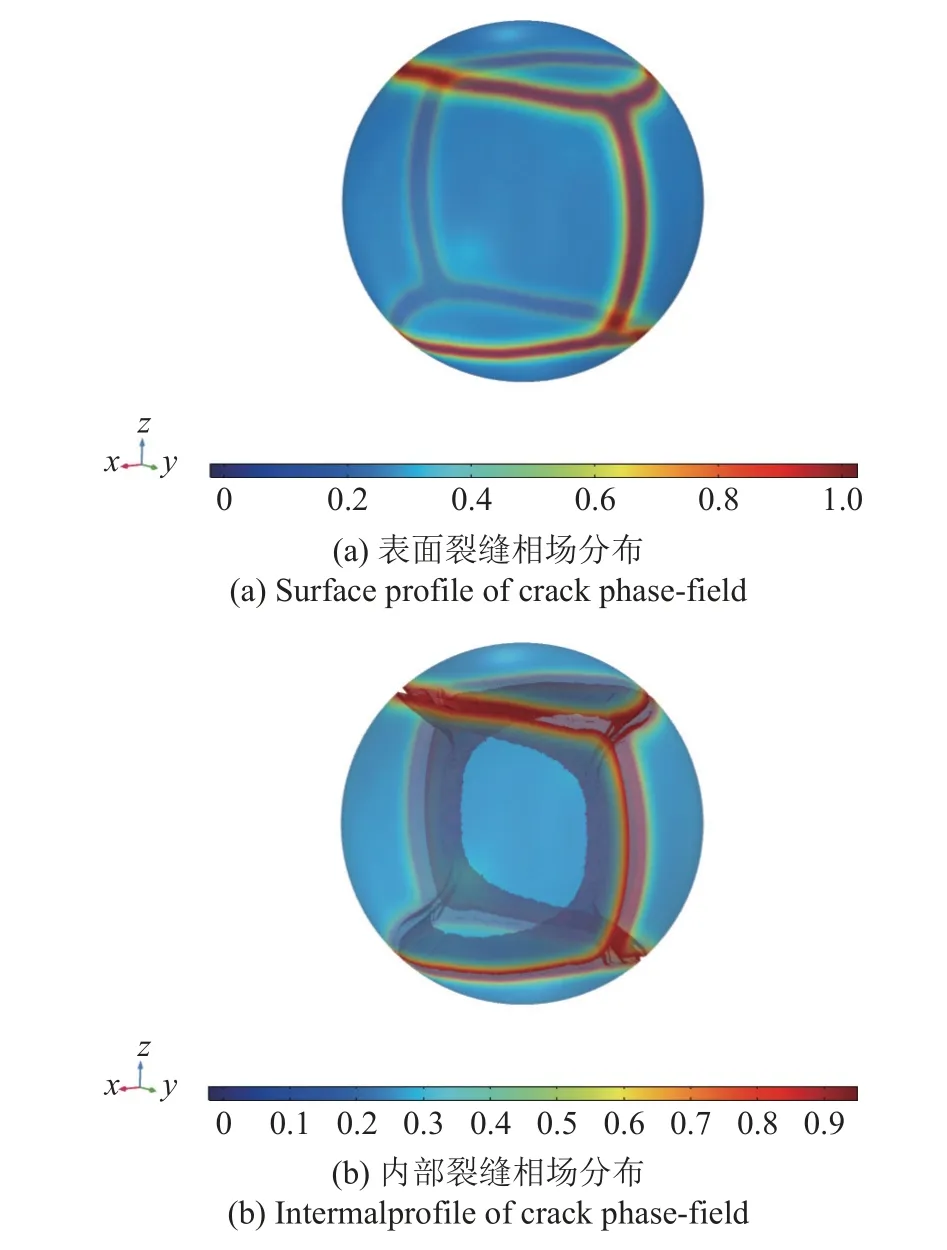
图22 球体电极颗粒三维分析: 裂缝相场分布云图Fig.22 Spherical storage particles: Profiles of the crack phase-field

结合图22 中给出的主应力分布,最终破坏时球体电极颗粒表面的裂缝带大致可以归为两类: (1) 靠近上、下两极处沿纬度方向的两条环向裂缝,受第一主拉应力驱动;(2)沿经线方向的竖直裂缝,受第二主拉应力驱动.由于第一、二主拉应力大小相等而方向正交,故两类裂缝几乎同时出现,最终分布也近似垂直.

为进一步研究球体电极颗粒内部的裂缝演化过程,沿X-Z平面切割球体,其剖面上的裂缝相场演化过程如图23 所示.有趣的是,该剖面上的裂缝相场演化与二维圆柱体电极颗粒(无初始缺陷的完好电极)基本相同.究其原因,对于X-Z剖平面,与之垂直的第二主拉应力对该平面上的裂缝演化不起贡献,即裂缝发展仅由第一主拉应力驱动,因此其裂缝演化情况与二维分析结果一致.

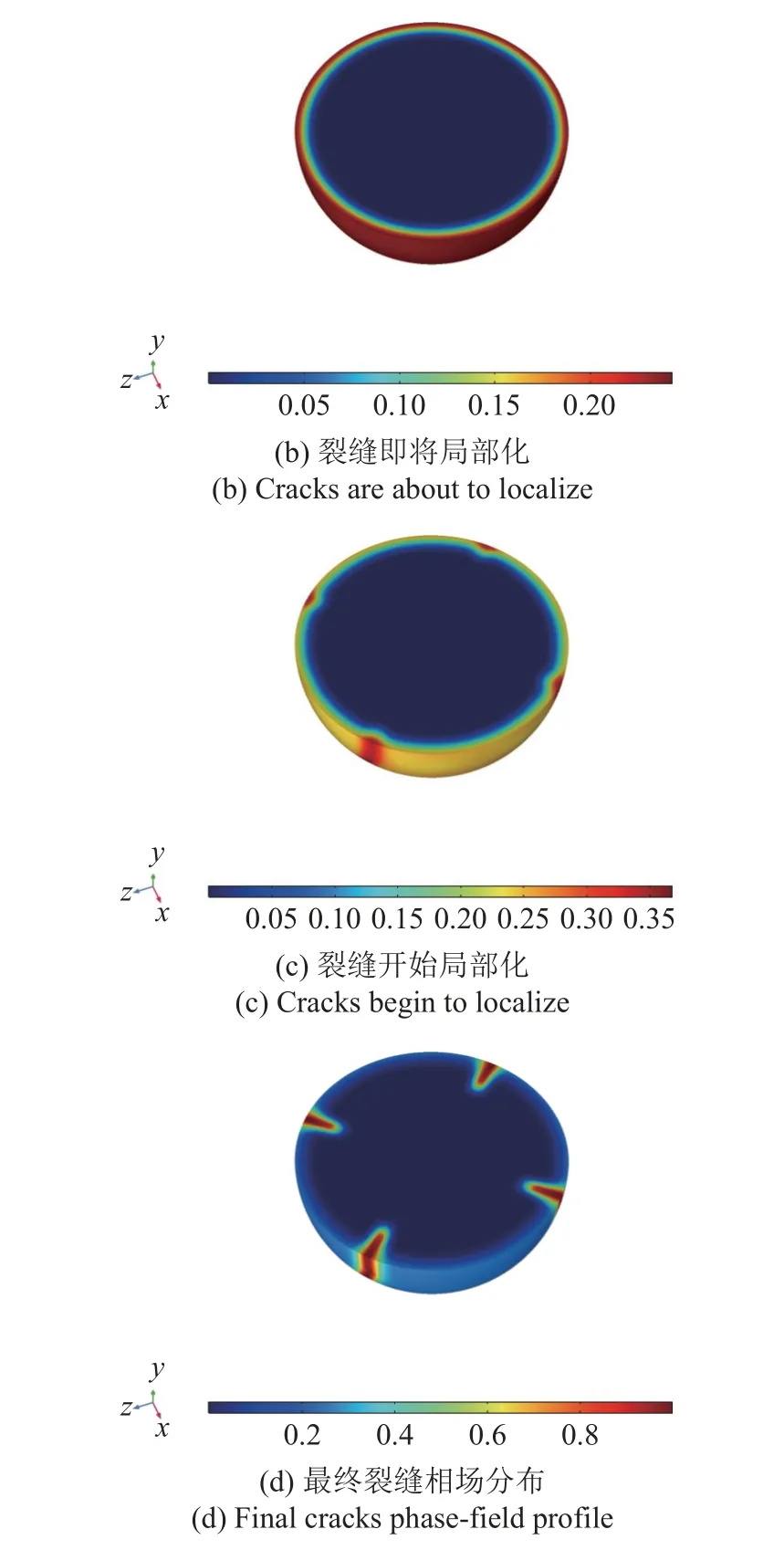
图23 球体电极颗粒三维分析: X-Z 平面裂缝相场演化Fig.23 Spherical storage particles: Evolution of the crack phase-field on the X-Z plane

4 结论与展望

在统一相场理论框架内,本文建立了化学扩散-力学变形耦合的相场内聚裂缝模型,发展了相应的多场有限元数值实现算法,并应用于锂电池电极颗粒裂缝演化导致的力学失效分析.

与纯力学作用下的相场内聚裂缝模型一样,上述模型同时融入了基于强度的裂缝起裂准则、基于能量的裂缝扩展准则以及基于变分原理的裂缝扩展路径判据,因此能够描述锂离子脱出过程中电极颗粒的复杂裂缝演化过程.

数值算例表明,所提出的化学-力学耦合相场内聚裂缝模型不仅能够描述带初始缺陷电极颗粒的开裂行为,而且同样适用于无初始缺陷的完好电极颗粒.由于数值模拟结果不受裂缝尺度和网格大小的影响,该模型能够应用于锂离子扩散过程中电极颗粒损伤破坏全过程的二维和三维分析,对商业锂电池电极的优化设计具有一定的指导意义.

需要指出的是,本文忽略了锂离子浓度变化对电极颗粒材料力学参数(如弹性模量等)的影响,且尚未考虑温度场对浓度分布和裂缝演化的耦合作用.这些问题将在后续研究中进一步加以考虑.

附录

为完整起见,这里给出圆柱体和球体两种形状的电极颗粒在弹性阶段的应力–离子浓度关系解析解.

(1) 圆柱体电极颗粒

采用极坐标 (r,φ) 表示圆柱体电极颗粒的平面应力状态.对于截面形状为圆形的电极颗粒,任意一点的剪应力 τrφ=0,应力状态由径向应力 σr和环向应力 σφ确定,且其应力状态不随角度 φ 改变,仅为径向距离r的函数.相应地,变形协调方程和线弹性应力–应变关系为

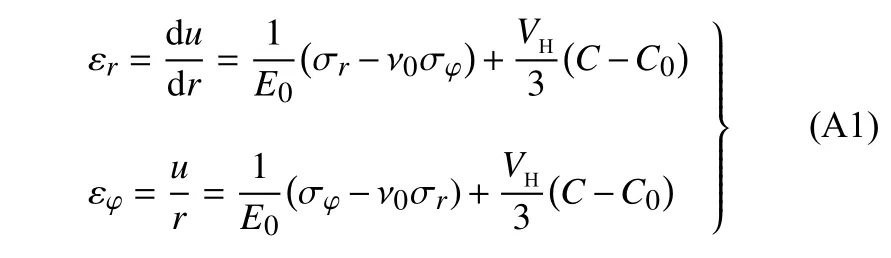
或表示为如下等效形式

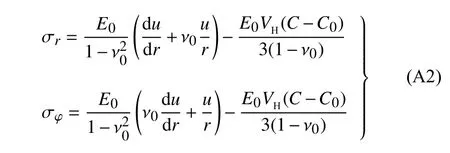
其中,E0和 ν0分别为材料的弹性模量和泊松比.将式 (A2)代入静力平衡方程

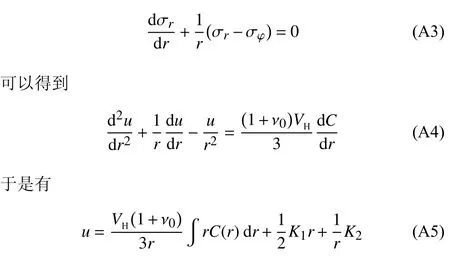
式中的积分常数K1和K2由以下边界条件确定:

①电极颗粒表面不受任何面力作用,径向应力为0,即σr|(r=r0)=0;

② 电极颗粒中心点r=0 处应力取极值(压应力最大),即

相应地,K1和K2确定为

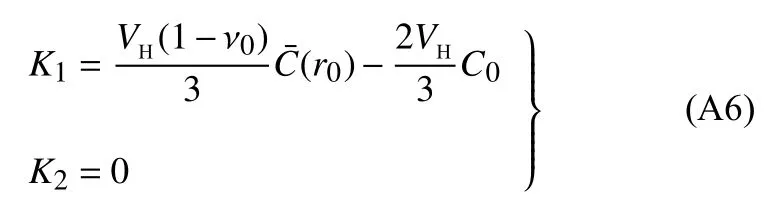
于是,径向应力 σr、环向应力 σφ 和静水压力 σH分别表示为

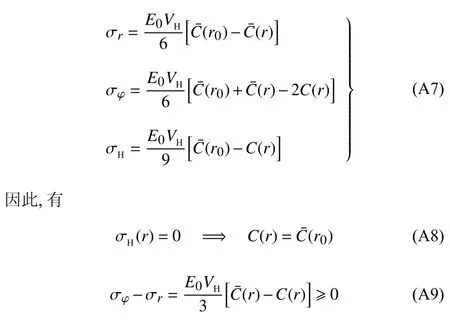
即静水应力 σH的拉压分界线 σH(r)=0 与电极颗粒的整体平均浓度等值线C(r)=C¯(r0) 重合.同时,对于脱锂过程,浓度分布从中心到外边界单调递减,故有 σφ≥σr,即最大主应力为环向应力.

(2) 球体电极颗粒

采用球坐标 (r,θ,φ) 表示球体电极颗粒的应力状态.此时,根据类似圆柱形颗粒的应力分析方法,可得出其极坐标下的应力解析解.由于几何中心对称性,剪应力 τrθ和 τrφ为零,应力状态由一个径向应力 σr和两个环向应力 σθ和 σφ完全确定且两环向应力在数值上相等.此外,对于球体几何形状,任意一点的应力状态不随转角 θ 和 φ 发生改变,仅为径距r的函数.

球体电极颗粒应力解析解推导过程与二维平面应力问题类似,最终其应力–离子浓度关系表示为

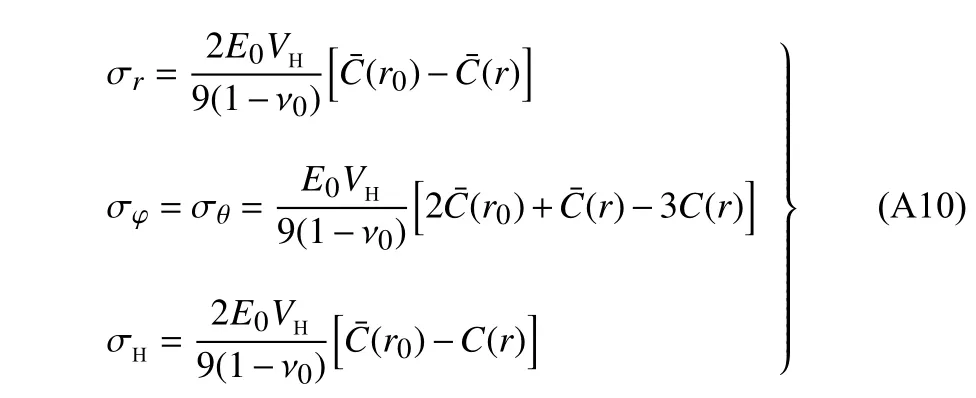
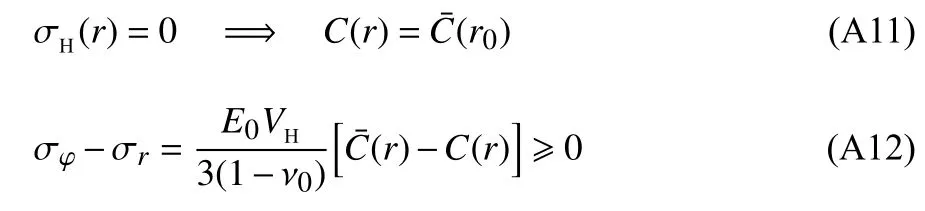
即静水应力 σH的拉压分界线 σH(r)=0 同样与电极颗粒的整体平均浓度等值线重合,且最大主应力同样为环向应力即 σφ≥σr.