高马赫数下激波液滴相互作用的数值模拟研究1)

宋家喜 潘书诚

(西北工业大学航空学院,西安 710072)

引言

液滴在高速气流作用下发生变形和破碎的研究可追溯至20 世纪50 年代,主要应用于大规模化学武器的高速投递、超声速飞行中的雨滴损伤评估以及火箭发动机的燃油喷射.例如,超声速飞行器在穿越大气层时会遇到暴雨,其雨滴在高速气流下的撞击和破碎会对飞行器表面材料造成严重损伤[1].早在1949 年,Hinze[2]通过实验确定了韦伯数(Weber number)为表征液滴变形和破碎过程的主要参数.此后,Hanson 等[3]以及Ranger 等[4]通过大量激波管实验发现液滴的变形破碎与周围剪切气流形成的边界层有很大关系,由此建立了液滴破碎的边界层剥离(boundary layer stripping)模型.Patel 等[5]通过实验研究了强表面张力下的液滴破碎行为,这种情形下Rayleigh-Taylor (RT)不稳定性波的穿刺(piercing)现象在液滴破碎中起着重要作用.另外,Pilch 等[6]对前人的研究工作进行了总结.根据不同的韦伯数,他们将液滴的破碎模态划分为经典的五种破碎模态,分别为振荡(vibrational) 破碎、袋状(bag) 破碎、袋蕊(bag-and-stamen) 破碎、剪切剥离[7](stripping)破碎和毁灭(catastrophic)破碎.为了弥补传统纹影显示技术的不足,Theofanous 等[8-9]采用激光诱导荧光技术来观测液滴破碎.其研究发现在高韦伯数下液滴的破碎是剪切诱导界面剥离的结果,而并非RT 波穿刺所导致.他们发现传统实验所观察到的毁灭破碎机制并不存在,只是液雾遮蔽效应的一种误导,从而对液滴破碎模态进行了重新划分.根据气动力相对于黏性力和表面张力的大小,他们将液滴破碎模态划分为低韦伯数下的RTP (Rayleigh-Taylor piercing)破碎机制和高韦伯数下的剪切诱导剥离(shear-induced entrainment,SIE)破碎机制.当气动力显著小于黏性力和表面张力时,RTP 是主要的破碎机制.而随着气动力的增加,SIE 将成为主导的破碎机制.

相比于实验测量,数值模拟能够捕捉到更详细的液滴界面和流场的演化细节,目前已成为研究液滴变形破碎的一种重要手段.但受限于目前计算能力,高分辨率的三维激波液滴相互作用数值模拟依然较难实现.前人的研究主要集中于激波冲击液滴的二维数值模拟[10-11]以及三维对称模拟[12-13].Kaiser 等[11]采用高分辨率的数值方法对二维液滴在高韦伯数下的变形破碎过程进行了数值模拟.结果表明,只有在足够精细的分辨率下液滴界面演化过程中迎风面的帽状结构才能得到充分解析.而黏性力和表面张力对于高韦伯数下液滴变形破碎的影响可被忽略.全三维的数值模拟在近几年也有出现,Meng 等[14]对液滴在高韦伯数下的SIE 破碎机制进行了数值模拟,定性描述了液滴的剪切剥离破碎机制和周围流场的演化等,包括前期液滴在激波冲击下的扁平化过程以及中后期剪切层破碎的形成.他们对液滴质心位移、速度和加速度的统计揭示了液滴在激波冲击下的加速推进[15]特征.另外,他们分析了液滴表面不稳定性,并对速度场进行傅里叶分解,试图找出液滴破碎后期非对称性形成的成因.随后,Dorschner 等[16]对中等韦伯数和无穷大韦伯数下的液滴破碎进行了全三维数值模拟和实验研究.他们发现液片的形成和脱落是一个反复循环的过程,Sharma 等[17]的实验也发现了这一点.通过对流场的方位角傅里叶变换,他们观察到了方位模态的发展,表面液滴破碎存在横向方位调节机制.但由于他们采用的是耗散界面方法,无法获取精确的液滴界面.因此,其数值模拟中观察到横向不稳定性的准确性还有待验证.

另外,近几年来有关其他参数对液滴变形破碎影响的研究也逐渐增多.Wang 等[18]实验研究了在恒定韦伯数情况下,通过不同材料流体的相互组合研究马赫数和雷诺数对液滴破碎的影响.他们的实验表明,在其他参数不变的情况下,随着来流马赫数从0.3 增加到1.2,液滴的破碎样式发生明显变化.他们还通过实验首次研究了两个串联液滴在激波冲击下的变形破碎行为,比较了不同韦伯数和串联液滴间距对液滴破碎行为的影响[19].Leung 等[20]设计了一款新型的激波管来研究高马赫数下激波和液滴的相互作用,通过对比数值模拟结果研究了2 到5 马赫数下激波冲击液滴的变形破碎过程.Nykteri 等[21]用一种多尺度的两相流方法数值模拟了轴对称液滴在1.6 至2.64 的马赫数区间的SIE 破碎机制,描述了液滴从早期到晚期的变形和破碎行为.Garcia-Magarino 等[22]通过对乙醇液滴破碎的实验研究发现了一种新的破碎模态,这在以前的类水液滴破碎研究中还没有报道过.然而,由于实验条件的限制,极高马赫数(比如马赫数大于5 的高超声速条件)下激波和液滴相互作用相关实验的实现比较困难,与其对应的数值模拟研究也没有出现.因此,有必要利用数值模拟的优势开展极高马赫数下激波和液滴相互作用的相关研究.

国内学者也开展了许多有关液滴变形和破碎的研究.陆守香等[23]在2000 年对激波冲击下的液滴变形破碎进行了数值模拟,并提出了初始雾化时间的概念,分析了液滴的变形破碎特征.耿继辉等[24]对液滴的变形破碎行为进行了较为系统的实验方面的研究.实验结果表明低韦伯数下液滴的变形破碎时间明显更长,初始液滴形状对液滴的变形破碎有着显著影响.楼建锋等[25]将VOF (volume of fluid)方法和湍流模型组合,数值模拟了相关实验,计算结果表明韦伯数对液滴变形破碎起促进作用.杨威等[26]采用简化的CLSVOF (coupled level-set and VOF)算法以及自适应网格加密技术对液滴在气流中的破碎过程进行了数值模拟研究.其结论解释了低韦伯数下液滴破碎和RT 不稳定性波的关系.另外,他们首次对低韦伯数下的液滴变形和破碎进行了三维数值模拟,解释了此时RT 波的重要作用[27].朱万里等[28]数值模拟了不同气流压力对液滴在SIE 破碎模态的影响,重点关注液滴破碎后小液滴的大小分布状态,结果发现较高的气流压力会显著增加液滴的变形.施红辉等[29]在水平激波管中进行了超声速条件下激波冲击亚毫米液滴变形破碎的实验研究,得到了各种韦伯数下液滴变形破碎的纹影图像.中国科学技术大学的丁航教授团队[30-31]发展了高精度的守恒清晰界面可压缩多相流数值方法,并将其应用于激波冲击液滴数值模拟研究.另外,有关黏性液滴[32-33]、非牛顿液滴[34]以及反射激波对界面不稳定性的影响[35]最近几年也有学者研究.就目前的研究进展来看,国内对于液滴变形和破碎的全三维数值模拟还较为缺乏,有关各个无量纲参数对液滴破碎的影响以及液滴在推进和变形过程中的定量研究也较为缺乏.

本文的主要工作是在高韦伯数的前提下,针对高马赫数和极高马赫数下液滴变形破碎动力学开展数值模拟研究.根据Kaiser 等[11]的高韦伯数下二维液滴变形破碎的有关结论,液滴的表面张力和黏性力可以忽略不计.本文采用基于守恒清晰界面方法的可压缩多相流数值模拟方法[36-39]来捕捉液滴界面的变形和流场演化,并使用自适应多分辨率方法来提高模拟精度和效率.其中,单元面通量采用5 阶WENO 格式[40]进行重构,时间积分使用二阶Runge-Kutta 格式[41].数值计算程序为文献[37]中开发的自适应多分辨率多相流计算程序ALIYAH.本文的结构如下: 第1 章描述所研究的激波液滴相互作用问题的物理模型;第2 章说明所使用的多相流数值模拟方法;第3 章验证数值模拟结果的准确性并分析高马赫数下液滴推进变形和破碎的数值模拟结果.

1 物理模型

1.1 问题描述

本文的研究对象为单个液滴在超声速和高超声速气流冲击下的变形破碎行为.在数值模拟中,液滴周围气体的高速流动通过一道正激波产生.激波马赫数定义为激波速度和声速的比值,即

其中,us代表激波速度,a为声速.液滴的变形破碎过程受惯性力、黏性力和表面张力的共同作用.惯性力驱使液滴发生变形最终破碎,黏性力阻碍液滴的变形,表面张力促使液滴保持原始的球形形状.在液滴的变形破碎过程中,韦伯数We和奥内佐格数Oh为描述该物理过程最重要的两个无量纲参数.We定义为液滴受到的惯性力和表面张力的比值,即

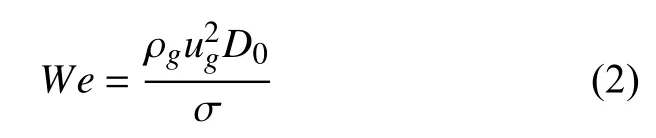
其中,ρg和ug分别为激波后的气流密度和速度.D0代表液滴的初始直径,σ=0.073 N/m 为液滴的表面张力系数.Oh定义为液滴受到的黏性力和表面张力之比,即

式中,μl和 ρl分别代表液滴的黏性系数和密度,D0代表液滴的初始直径.其中,本文算例中的液滴黏性系数为1 mPa·s,密度为1 t/m3.

物理计算域如图1 所示,沿流向取6 倍的液滴初始直径,沿展向和垂向都为4 倍的液滴初始直径.这样的计算域大小既避免了液滴受到壁面反射的影响过大,又不至于因为计算域太大而导致过高的计算量.首先模拟384×256,768×512 和1536 ×1024 三种有效网格分辨率下的二维算例.在充分平衡计算所需代价和数值模拟效果之后,最终选择使用分辨率为768×512×512 来进行全三维液滴破碎的数值模拟,这部分的内容会在3.1 节进行详细分析.与Meng 等[42]的研究类似,这样的分辨率相当于沿液滴直径布置128 个网格.如图1所示,为了真实模拟实验中的激波管壁,计算域前后上下面均设为对称边界条件,而左右界面分别为入流和出流边界条件.液滴的初始形状为直径3.5 mm的球形.其中心位于矩形计算域的中轴线距左边界5.5 mm 处,而激波初始位置位于液滴中心前2.0 mm处.液滴初始密度 ρl=1 t/m3,激波前空气密度为1.2 kg/m3,激波前空气压为100 kPa.根据Rankine-Hugoniot 激波关系式计算得出不同激波马赫数Ms的流动参数如表1 所示.

图1 激波驱动液滴破碎数值模拟的计算域Fig.1 Computational domain for shock-driven droplet breakup

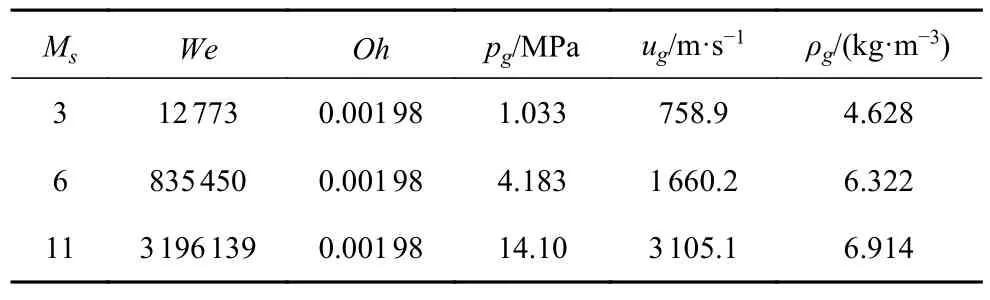
表1 不同激波马赫数下的激波后流动状态Table 1 Flow conditions behind various Mach air shocks

1.2 控制方程

本文研究液滴破碎所使用的控制方程为

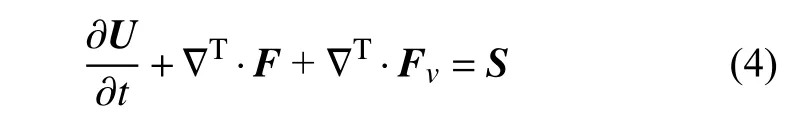
其中U=(ρ,ρu,E)T为守恒量,F=(uρ,ρu⊗u+pI,u(E+p))T为对流通量,Fv=(0,T,T·u)T为黏性通量,S代表考虑表面张力的源项.t为物理时间,ρ 代表密度,u为速度矢量,T为黏性应力张量.E为总能量,p代表压强.控制方程需要加入状态方程得到封闭,对于空气,使用理想气体状态方程

而水的状态方程采用Tait 状态方程

其中,γ=7.15,A=100 kPa,B=331 MPa,ρ0=1 t/m3.

2 数值方法

2.1 基于守恒清晰界面模型的可压缩多相流数值方法

在笛卡尔网格下将控制方程在计算域 Ω 内使用有限体积方法进行离散,计算域 Ω 被随时间演化的两相界面划分为液相域 Ω1(t) 和气相域 Ω2(t).图2 给出了二维笛卡尔网格下的清晰界面方法示意图,其中 ΔΓi,j(蓝色直线) 代表每个网格单元内对精确界面(红色曲线)的分段线性近似.对控制方程在每个子域 Ωn(t) 和网格单元 Δi,j的交集 Ωn(t)∩Δi,j内进行积分并应用高斯定理可得,

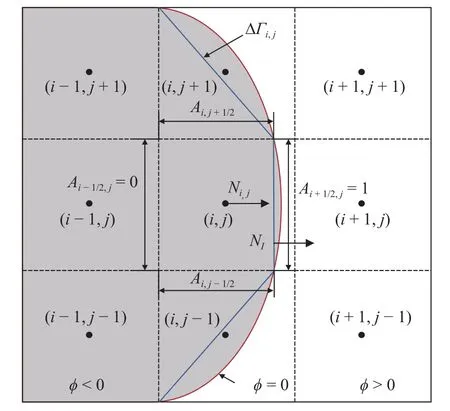
图2 二维切割网格下的守恒离散示意图Fig.2 Two-dimensional schematic of the conservative discretization in a cut cell

其中 Γ(t) 为每个网格单元随时间变化的由level-set函数[43]确定的分段界面. ∂Δi,j为每个网格单元的边界.n为网格单元边(2D)或面(3D)的单位法向量,而nΓ代表界面的单位法向量.Ωn(t)∩Δi,j的体积为αi,jΔi,j,其中αi,j为体积分数,∂ (Ωn(t)∩Δi,j) 在网格(i,j)内可以用近似,其中A如图2 所示为∂Δi,j被ΔΓi,j切割后的剩余量.这样式(7)可表达为

将上式扩展到三维可得

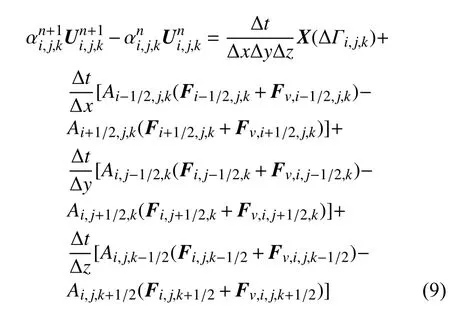
其中,Δt为时间步长,代表n时刻网格单元(i,j,k)的单元平均状态量,Fi,j,k为单元的界面通量,X(ΔΓi,j,k)为气液界面交换项.对式(9)在单相流场上进行求和可得

右手边的第二项为界面交换项,只存在于被切割的网格单元.对整个计算域的两相流体来说,界面交换项的符号相反.对整个两相流体进行求和可得

这说明对两相流体来说,本方法在全局上是守恒的.更多关于守恒性的验证可参考本数值方法的文献[36].最大时间步长根据CFL 数来确定,本文中使用的CFL 数均为0.5.两相界面通过水平集函数φ(x)来描述,即 φ(x)=0 代表两相界面,φ(x)＜0 代表流体1,φ(x)＞0 代表流体2,|φ(x)| 为单元网格x的中心坐标距离界面的距离.水平集函数的演化用以下的对流方程描述

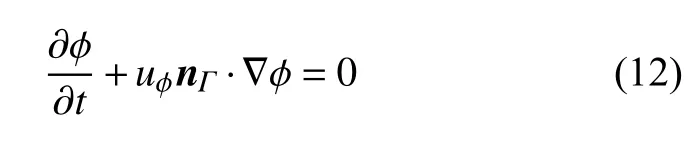
其中,uφ代表水平集对流速度.在被界面切割的单元里面,uφ等于界面速度uΓ,uΓ可以通过在相界面求解一个两种物质的黎曼问题来得到[36].平均曲率κ为界面法向矢量的散度,而界面法向矢量nΓ可以通过以下求解得到

在未被界面切割的单元中,水平集对流速度等于外推得到的界面速度可由扩展方程(extension equation)的稳态解得到

为了维持水平集函数的符号距离特性 |∇φ|=1,需要对水平集函数进行重新初始化[44]

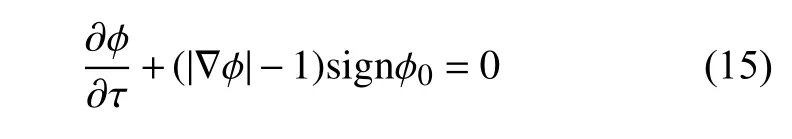
这里 φ0指重新初始化开始之前的水平集场.为了获取界面附近网格点的流体状态量,通过虚拟流体法(ghost fluid method)[45]将界面一侧流体状态量外推到另一侧

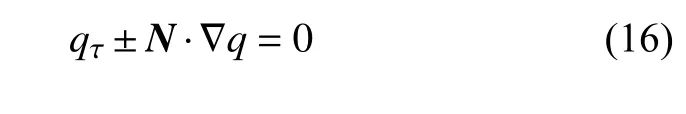
其中,q代表需要外推的流体状态量,而N≡(Nx,Ny,Nz)是根据水平集函数确定的界面法向量.另外有关单元孔隙A、单元体积分数 α,以及界面交换项X的推导细节可以参考图2 和文献[36-39].

为了统计液滴推进和变形,本文用以下公式计算液滴质心位移xc、速度uc和加速度ac

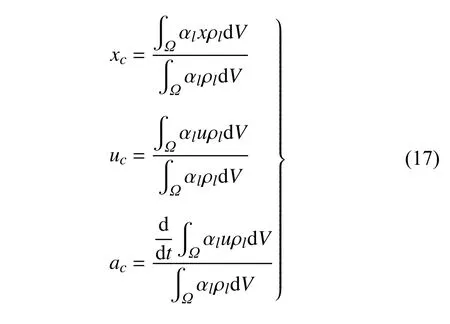
其中,αl,x,ρl,V,u分别为网格单元的液相体积分数、流向坐标值、密度、单元格体积和速度.液滴质心位移、速度和加速度分别使用下式进行无量纲化

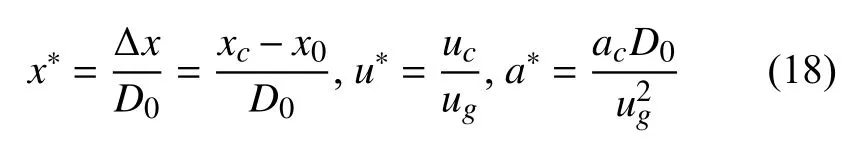
式中,x0为液滴初始位置的球心坐标,D0为液滴的初始直径,ug为激波后的气流速度.另外,本文所提到的液滴破碎时间均为无量纲时间,使用文献[4]中提出的公式对液滴破碎时间进行无量纲化,其中

式中,ρg和 ρl分别为激波后的空气密度和液滴密度.

2.2 基于块结构的自适应多分辨率网格加密方法

在液滴破碎的过程中,为了精确捕捉到液滴界面的变形,需要在液滴界面和激波附近布置足够精细的网格,而其他地方使用较粗的网格以节省计算量.为此,应用一种基于块结构的自适应多分辨率方法[37,46],这种方法由动态数据结构和自适应更新过程组成.在自适应更新过程中,网格的粗化和细化过程通过投影算子Pl+1→l和预测算子Pl→l+1来实现,以一维结构网格为例,两者分别定义为

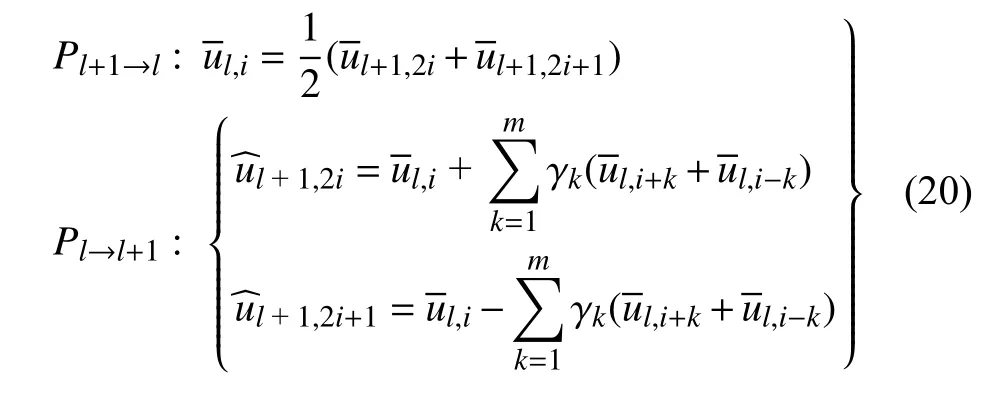
这样,使用投影算子Pl+1→l从l+1 层网格单元计算得到l层网格单元的过程是精确的,而利用预测算子Pl→l+1根据l层网格单元来预测l+1 层网格单元的值会产生一定的预测误差.l层第i个网格单元的预测误差可以定义为在本文的工作中,采用五阶插值来定义预测算子,即m=2,相应的系数为

当预测误差大于某一个阈值时,相应的单元或块结构将会被细化,这个阈值定义为

其中,D0为空间维度,Lmax为自适应数据结构的最大层数,ε 为参考误差值.另外,始终使用最密的网格捕捉界面.这样,如图1 所示,在界面和流场剧烈变化(如激波)区域加密网格.

3 结果分析

3.1 网格分辨率的影响

完全解析激波和液滴相互作用问题中所有的物理细节需要的计算量对于目前计算机很难承受.根据Popinet[47]的研究,完全解析液滴表面张力影响所需的网格尺度可按照单元格韦伯数来进行估算

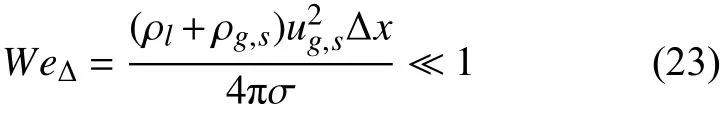
按照这样的估算,仅仅解析Ms=3 下的相关算例就需要沿液滴直径布置2.2×106个网格,这样的全三维数值模拟所需的网格量达到了惊人的 1021,这远远超出了目前超级计算机的计算能力.此外,根据Chang 等[12]的研究,为了捕捉液滴破碎过程中的KH 不稳定波,他们使用了八层自适应网格,相当沿液滴直径布置800 个网格.对于黏性边界层的捕捉,另外还需在液滴表面沿直径布置4000 个网格,这样的计算量也超出了绝大多数计算机的计算能力.因此,为了使计算量可以承受,本文把研究的主要关注点放在液滴界面的变形、液滴加速过程的量化以及流场结构的演化上.首先对不同网格分辨率下的结果进行比较以验证计算结果的收敛性.随着计算网格的不断细化,数值模拟可以捕捉到更加精细的流场结构和界面变形的细节,但随之增加的计算代价是巨大的.因此,需要选择一个合适的网格分辨率,既能捕捉到相对完整的界面变形特征,又能尽可能地节省计算量.

如图3 所示,在激波马赫数为3 的情况下三种不同网格分辨率的二维液滴破碎数值纹影图表明液滴的界面变形和流场结构具有相似的演化趋势.显然,分辨率越高,捕捉到的液滴界面和流场结构越精细.在最粗的384×256 分辨率下,尽管液滴的整体变形特征与768×512,1536×1024 分辨率下类似,但界面结构特征的细节还不够完善.液滴上游的帽状结构没有捕捉到,赤道区域的剪切层也未捕捉到.对比768×512 和1536×1024 下的界面变形和流场结构可以发现,768×512 分辨率已经能够捕捉到相对完善的界面特征和比较精细的流场结构.

图3 不同网格分辨率下的数值纹影图Fig.3 Numerical schlieren images for various grid resolutions

图4 统计了三种网格分辨率下液滴质心的无量纲位移和无量纲速度随时间演化规律.384×256 分辨率下的液滴质心运动曲线和另外两者在后期有显著差异,其可能原因是由于加密后的网格能够解析出从原始液滴剥离形成的薄液片和小液滴,而小液滴的存在使得液滴整体的质心变得靠后,导致384 ×256 分辨率下液滴后期的位移和速度明显低于其余两者.由于768×512 和1536×1024 下质心运动曲线之间的差异已经相当的微小,为了节省计算资源,后续采用768×512×512 的分辨率来进行液滴破碎的全三维数值模拟.这样的网格分辨率足以捕捉到相对完整的界面演化状态和液滴的加速运动规律,相对而言计算量也在可接受的范围之内.

图4 不同网格分辨率下的无量纲质心位移和速度演化Fig.4 Evolution of the dimensionless center-of-mass drift and velocity for various grid resolutions

3.2 液滴表面张力和黏性的影响

一方面,在高We和低Oh下,气动力为驱使液滴变形破碎的主导机制.此时液滴的表面张力和黏性力在抵抗液滴破碎的过程中所起到的作用相当微弱,表面张力和黏性力在量级上是可以忽略不计的.另外一方面,目前的网格分辨率根本达不到完整捕捉液滴表面张力造成的毛细效应的影响.

为了验证表面张力和黏性作用,在768×512 的网格分辨率下,分别模拟了在忽略表面张力和黏性力以及考虑表面张力和黏性力2 种条件下的二维液滴破碎行为.如图5 所示,在激波马赫数为3 的条件下,表面张力和黏性力对液滴界面变形的影响甚微,仅仅从尾涡的充分发展区域才能发现微小的差异.另外,如图6 所示,两种情形下的液滴质心位移、速度和加速度曲线几乎完全一致.唯有液滴破碎中后期的加速度曲线有所出入,这一出入更多是数值误差引入的振荡,并非由表面张力和黏性力导致.经过如上对比,在高We、高Ms和低Oh下,表面张力和黏性模型可以被忽略,故在进行液滴的全三维数值模拟过程中忽略表面张力和黏性力的影响,这也与Kaiser 等[11]的做法一致.

图5 表面张力和黏性力对激波冲击液滴数值纹影图的影响Fig.5 Effects of capillary and viscous forces on Numerical schlieren images for shock-droplet simulations

图6 表面张力和黏性力对液滴无量纲质心位移、速度和加速度演化的影响Fig.6 Effects of capillary and viscous forces on evolution of the dimensionless center-of-mass drift and velocity and acceleration for shock-droplet simulations

3.3 和实验结果的比对

图7 和图8 为不同视角下Ms=3 的激波冲击液滴变形破碎的界面演化图,上面一行为数值模拟结果,下面一行为相应无量纲时间下的实验结果.实验数据来源于Theofanous 等[9]的实验,其激光诱导荧光可视化技术显示了液滴在激波冲击下的变形破碎过程.实验所使用的液滴直径和数值算例均为3.5 mm,并且激波马赫数均为3.尽管实验使用的液滴黏性和表面张力与水不同,但其SIE 机制是相似的.值得注意的是,原始实验数据的激波运动方向是从右向左的,而本文所有数值模拟结果的激波运动方向均为从左至右.为了方便和数值模拟结果做比较,将实验结果的图片旋转 180°.

图7 数值模拟结果(上)和实验可视化(下)侧视图对比Fig.7 Comparison of numerical results (upper) and experimental visualizations (lower) for side view

图8 数值模拟结果(上)和实验可视化(下)前侧30°视图对比Fig.8 Comparison of numerical results (upper) and experimental visualizations (lower) for 30° front side view

从图中可以看出,数值模拟得出的液滴破碎形态、破碎时间都和实验结果吻合,表明该方法可以有效捕捉液滴破碎过程中的界面变形.激波冲击过后,液滴在高速气流的作用下发生迅速的扁平化.在扁平化的过程中液滴迎风面的前驻点区域一直保持光滑,临近赤道区域出现凸起.同时液滴背风面逐渐变平,赤道区域在气流剪切作用下拉伸出薄的液层.在实验和数值结果中均可观察到这些SIE 破碎机制的显著特征.当然,目前所允许的分辨率所计算出的结果还不足以捕捉到SIE 破碎机制的全部特征,比如实验观察到的液滴背风面在扁平化的过程中会出现带状条纹.据Chang 等[12]的研究,这是KH 不稳定性在液滴表面不断发展的结果,当然目前的分辨率还不足以捕捉到液滴表面的KH 波.而液滴赤道区域被拉伸的液层在早期就已经出现破碎形成小的细雾,这些破碎特征在数值模拟中可能需要更高的分辨率才可以捕捉到.

3.4 界面的演化及流场分析

图9 为激波冲击液滴前期(t*=0.029 48) 的对称面上的数值纹影 lg(|∇ρ|+1) 云图,显示了流场的波系结构演化.入射激波到达液滴的上游面会形成反射和透射.如图9 所示,由于液滴的密度和声速远远大于周围气体,为了在界面处满足力学平衡[48],液滴迎风面会形成一道向上游传播的反射激波,而一部分入射激波穿透液滴表面形成透射激波.

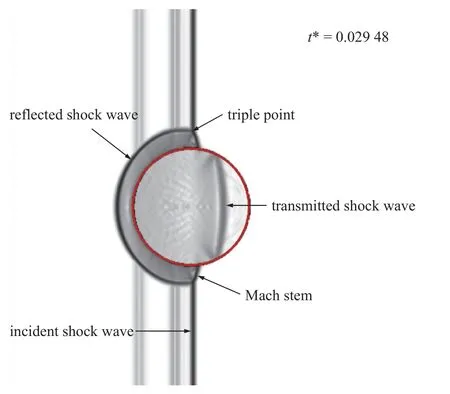
图9 Ms=3 的激波冲击下流场的早期数值纹影图Fig.9 Numerical schlieren images for Mach 3 simulations at early stage

由于液滴的可压缩性远小于周围空气,液滴内部透射激波的运动速度要快于周围入射激波的速度.透射激波在撞击到液滴下游界面处再次发生反射,形成膨胀波.膨胀波向液滴上游传播,由于液滴下游界面存在曲率,膨胀波在液滴内部发生汇聚,形成一个低压区[49].随着入射激波和两相界面的夹角超过临界值,规则反射向马赫反射转变,形成马赫杆[50].马赫杆在液滴的下游驻点处汇聚,形成二次波结构.液滴赤道处脱落的微雾在一对反向涡的作用下形成了二次循环区[49].如图10(a)所示,液滴的变形程度并不明显,而随着二次波系统和二次循环区的形成(见图10(b)～图10(f)),在周围气流的影响下液滴开始发生扁平化,受剪切作用,液滴赤道处液片受到拉伸变薄,随后发生破裂.

图10 Ms=3 的激波冲击下流场的数值纹影图Fig.10 Numerical schlieren images for Mach 3 simulations

图11 中的液滴流场压力云图表明随着入射激波扫过液滴的后缘,周围气流压力的不均衡导致了液滴的推进和变形行为.从图11(a)可以看到,液滴的前驻点区域压力最大,而后驻点区域压力较小,液滴在此压力场的作用下开始向下游推进.相比于前后驻点处的压力,液滴赤道区域的压力明显更低,这样的压力差导致了液滴的扁平化行为.图12 中的涡量云图,气流流过液滴最大直径处,在液滴的背风面产生了分离,分离的气流形成了一对明显的涡.如图12(b)所示,随着主涡不断向下游扩展,背风面的流动分离处又产生了一对与主涡方向相反的二次涡,如图12(c)和图12(d),这两对涡的相互作用导致了液滴尾流区域的形成,也导致了液滴赤道区域的剪切剥离过程.

图11 Ms=3 的激波冲击下流场的压力云图Fig.11 Pressure contours for Mach 3 simulations

图12 Ms=3 的激波冲击下流场的Z 轴方向的涡量云图Fig.12 Z-Vorticity contours for Mach 3 simulations

3.5 液滴的循环破碎过程

液滴破碎在更高的马赫数下更加剧烈和清晰,因此通过Ms=11 情形的模拟结果来分析液滴的破碎过程.图13 中显示了液滴在Ms=11 的激波冲击下的前侧 45°界面演化图,为了方便观察薄液膜和小液滴，采用光线追踪技术渲染模拟结果.如图中的箭头和虚线所标识,液滴在激波驱动下的整个破碎过程包含了三个重复的破碎模式.液滴在激波的冲击下从初始球形破碎为小液滴并非只经历了一次性的SIE 破碎,而是逐阶段发生的,每次都会经历相似的破碎过程.首先,液滴的赤道处受到剪切拉伸变为薄的液片,继续拉伸导致液片较薄的地方出现破损而形成破洞.破洞逐渐扩展合并形成韧带,最终韧带的变细以及其互相撞击导致破碎为小液滴.

图13 Ms=11 下激波冲击液滴破碎的光线追踪渲染(前侧45°视图).第一次到第三次破碎分别使用箭头、红色虚线和蓝色虚线来标识Fig.13 Ray-traced rendering of shock-droplet breakup for Mach 11 simulation (45° front side view).The first to third breakup are identified by arrows,red dotted lines and blue dotted lines,respectively

图13 分别对每次液滴破碎做了标记,箭头、红色虚线和蓝色虚线分别代表了液滴第一次、第二次和第三次的破碎过程.液滴下一次的破碎并非是在上一次破碎全部完成之后才开始的,其之间存在重叠.例如,在t*=0.103 6 时刻,第二次破碎刚刚进行到破洞形成的阶段,此时液滴赤道处就已经拉伸出第三次破碎前期阶段的薄液片了.这种重复循环的破碎机制会一直持续到液滴完全破碎为小液滴以至于主液滴已经无法在赤道拉伸出薄液片为止.虽然这种循环破碎在本文记录的时间范围内只重复了三次,但其是周期发生的.在最近有关液滴破碎的相关研究中,同样发现了这种循环破碎的现象[16-17].在Dorschner 等[16]的实验中,他们发现液滴从破碎开始到结束一共经历了四次循环的破碎过程.同时,他们还测量了每次破碎发生的时间,破碎时间定义为液片从主液滴开始脱落的时间,也可以理解为薄液片出现破洞的时间.在韦伯数趋于无穷大的情况下,液滴第一到第三次破碎的时间分别为t*≈0.5,t*≈1.0和t*≈1.6,对应图13(c)、图13(f)和图13(h).这验证了本文的数值模拟结果和Dorschner 等[16]的实验结果是相吻合的.根据他们的推断,这种逐次循环破碎行为可能和变形后液滴的涡脱落有关.

3.6 马赫数对激波冲击液滴的影响

一直以来,We和Oh被认为是控制液滴变形最重要的两个无量纲参数,故以往大多数学者都会把研究重点放在不同韦伯数下液滴变形和破碎的相关研究上,而关于其他无量纲参数对于液滴变形破碎的影响却极少被研究.为了填补这一空白,利用数值模拟相对于实验研究更易实现高马赫数环境这一特点,本文研究了高马赫数情形下马赫数对液滴变形和破碎的影响.根据Theofanous 等[9]的实验研究,高韦伯数下SIE 破碎机制为液滴的主导破碎机制.为了验证这一结论,对比Ms=3 ,Ms=6 和Ms=11 三种马赫数下液滴的变形破碎过程.

如图14 所示,使用无量纲时间将3 种马赫数下液滴的界面演化过程缩至同一时空尺度下.结果表明不同马赫数下液滴的界面演化形态并无二致,基本可以归为两个阶段: (1)首先,t*=0～0.3 时,液滴在周围气流压力差的作用下发生扁平化行为,液滴赤道区域的剪切剥离还未开始,此时液滴基本上可以看作一个刚体,质心不会出现过大的偏移;(2)然后,在t*=0.3～0.6 阶段,随着液滴赤道区域剪切剥离的开始,液滴扁平化和剪切剥离同时进行,液滴逐渐发生破碎行为.

图14 不同马赫数下的液滴界面演化过程Fig.14 Evolution of the droplet interface for various Mach air shocks

虽然三种马赫数下这两个阶段基本一致,但液滴的局部变形形态有所差异.在液滴扁平化的过程中,Ms=3 的液滴迎风面区域基本保持光滑,而背风面在t*=0.2 时就开始变平,之后基本都处于这种状态.随着马赫数的提高,液滴背风面的扁平化程度有所下降,根据图11 的压力云图可以定性分析这一现象产生的原因.在Ms=3 的情况下,液滴迎风面始终处于一个压力较高的状态,如此较为均匀的压力分布使得液滴的迎风面得以保持光滑.随着气流在液滴的赤道处发生分离,液滴的赤道偏向背风面处形成了一个低压区.在液滴的尾流区,马赫杆的汇聚在液滴的尾流区形成了一个高压区,如图11(a)所示.液滴的背风面在尾流高压区和赤道低压区的双重作用下被压扁变平.然而,在Ms=6 尤其是Ms=11 的算例中,由于激波的速度太快,马赫杆汇聚形成的高压区存在时间较短,液滴背风面扁平化不明显.在剪切剥离的过程中,高马赫数所受的剪切力更大,液滴较早发生剪切剥离,剪切剥离出的液层更薄.

接下来使用液滴流向直径和初始直径之比Dcro/D0以及横向直径和初始直径之比Dwise/D0来对液滴的变形过程进行定量研究.如图15 所示,液滴流向直径随时间以近似线性的趋势减小,而横向直径的增长表现出明显的非线性.仔细观察,液滴的横向膨胀可分为两个线性阶段.在液滴的扁平化前期,即t*=0～0.3阶段,液滴横向直径缓慢增长.而到了中后期的t*=0.3～0.6 阶段,由于赤道周围受到强烈的剪切拉伸,液滴沿横向迅速膨胀.

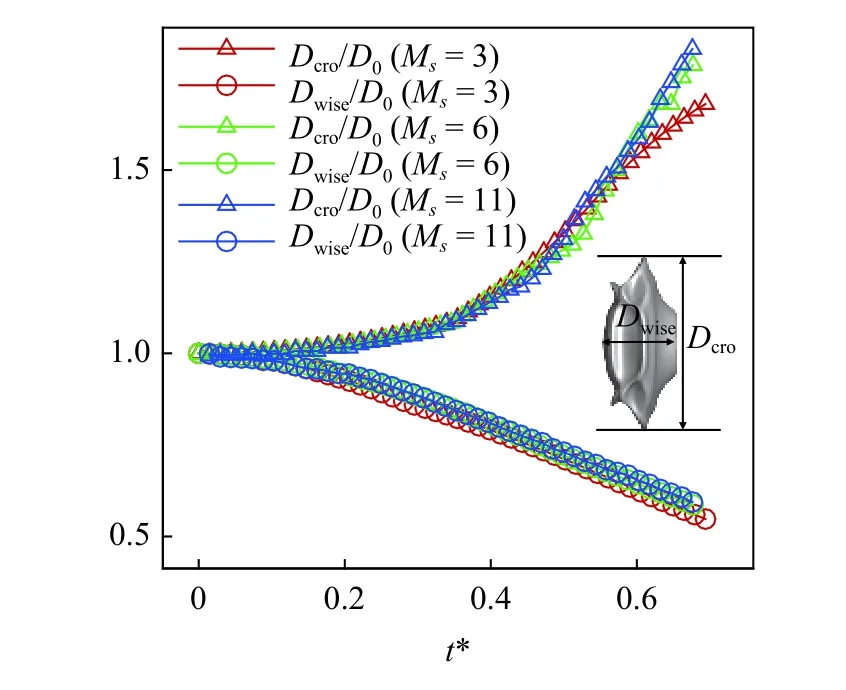
图15 不同马赫数下无量纲流向直径和无量纲横向直径的演化Fig.15 The evolution of the dimensionless cross-stream and the dimensionless streamwise diameter at various Mach air shocks

图16 对比了液滴质心的位移、速度、加速度以及拽力系数的演化曲线.液滴的质心位移、速度及加速度使用式(18)进行计算和无量纲化,而拽力系数[43]定义为

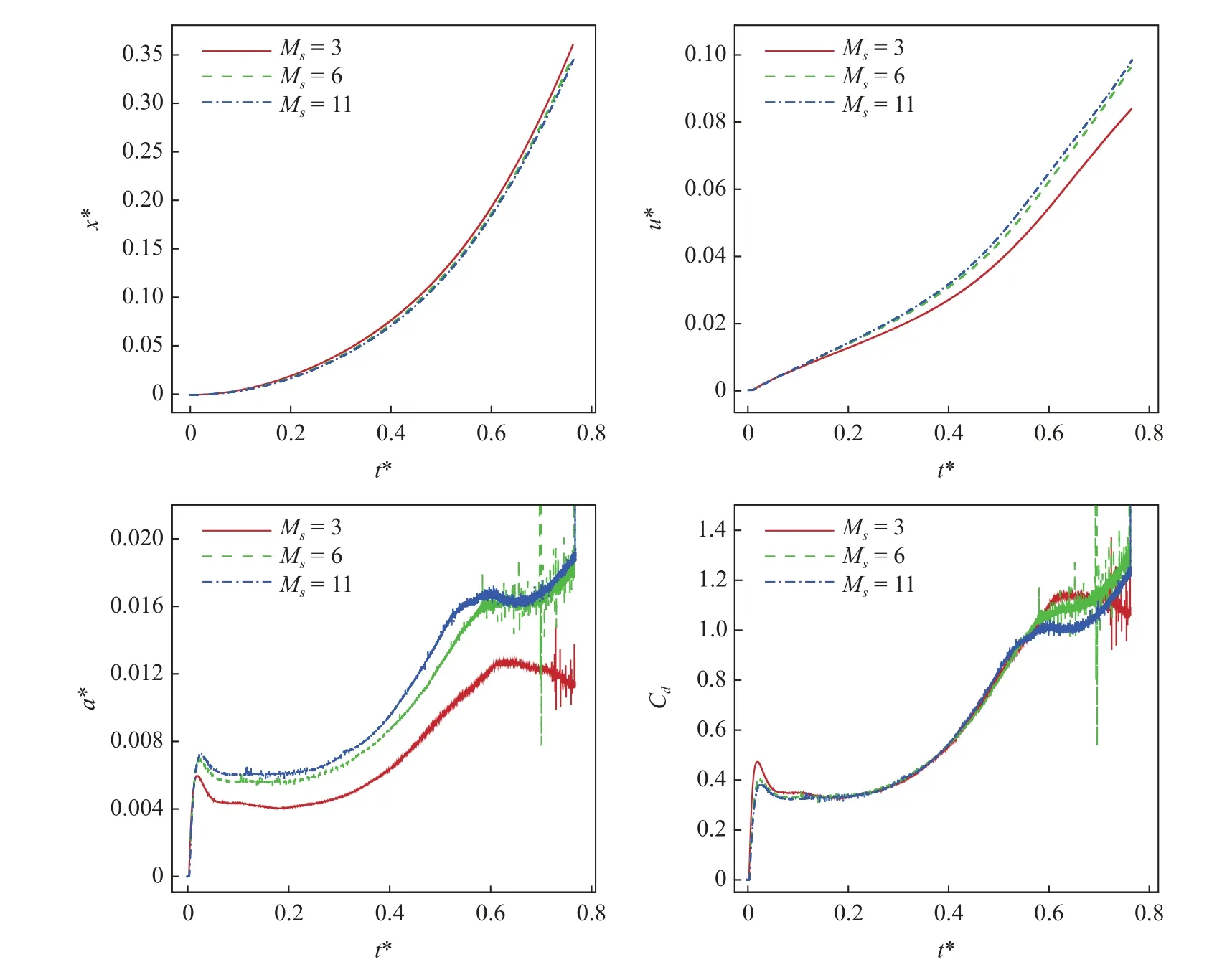
图16 不同马赫数下的无量纲质心位移、速度、加速度以及拽力系数演化Fig.16 The evolution of the dimensionless center-of-mass drift and velocity and acceleration and drag coefficient at various Mach air shocks

其中m为液滴的总质量

式中,ac为液滴质心加速度,ρg和ug分别为波后气体密度和速度,uc为液滴质心速度,Fd为液滴沿流向受力的总和.在液滴位移x*曲线中,三种马赫数下液滴的位移曲线的差异很小.然而,液滴的无量纲速度u*和加速度a*曲线却有所差异.随着激波马赫数的增加,液滴的无量纲速度和加速度也相应增大,这样的结果与Meng 等[43]在液滴的二维破碎模拟中所得到的结果一致.分析3 种马赫数下u*和a*曲线的演化,可以发现,随着马赫数的增加,液滴的无量纲速度和加速度的差异在逐渐减小.这表明在高超声速的情况下,马赫数对液滴运动的影响在逐渐减弱.

观察图16 中液滴无量纲速度和加速度曲线的差异,结合式(17)对无量纲参数的定义,这样的定义显然引入了密度和速度的分布.考虑到液滴沿着推进方向的运动其实在各个地方的速度是不均匀的,式(17)的定义本质上是液滴各微团推进速度和加速度的平均值.其实,还可以直接对液滴质心的位移曲线进行一次和二次求导来定义速度和加速度.这种情况下认为液滴是一个无形状的点.如图17 所示,这样求出的三种马赫数下的无量纲速度曲线基本吻合.这样做虽然可以得到不变性,但是相比于式(17)并不能更物理地表征液滴的变形,因为液滴并不是以相同外形和均匀速度进行推进的.另外,因为液滴质心位移曲线是根据积分表达式计算出的一系列离散的数值,而非解析表达式,对质心位移曲线求导时采用的差分离散近似会产生数值振荡过大的问题.在Meng 等[43]的研究中也讨论了这样的做法,这样求出的液滴速度加速度曲线存在较大的噪声误差(如图17 右).采用式(17)的定义能够将该噪声震荡最小化.

图17 直接对液滴质心位移求导得出的无量纲速度和加速度演化Fig.17 The evolution of the dimensionless velocity and acceleration derived directly from the dimensionless center-of-mass drift

参考液滴的拽力系数曲线可以发现,不同马赫数下液滴的拽力系数曲线除了在前期峰值和后期振荡区有明显差异,其他地方吻合得特别好.分析液滴的速度曲线发现速度的斜率并非是一个常数,即液滴并非是以一个恒定的加速度来运动的.正如前面所分析的,液滴的变形破碎过程可分为两个阶段,在t*=0～0.3的这一阶段,液滴的变形不明显,此刻液滴还可以看作一个刚体,以一个相对较小的恒定加速度运动.随着液滴扁平化的不断发展,液滴的迎风面积增大,所受到的气动力不断增加,故液滴的加速度也不断增大.随着剪切剥离的开始,液滴的加速度也开始出现较大的震荡,通过液滴的无量纲加速度曲线a*可以很清晰地看到这些振荡规律.Meng 等[14]的研究认为振荡的产生可能是旋涡脱落导致的,具体的振荡机制还需要采用更高分辨率进行更加深入的研究.

4 结论

在高韦伯数的前提下,本文对激波马赫数Ms从3 增加到11 时激波和液滴的相互作用进行了全三维数值模拟研究.求解得到的流场和液滴界面演化过程表明高马赫数(Ms=3)和极高马赫数(Ms＞5)下的液滴变形和破碎遵循统一的SIE 破碎机制.液滴的变形和破碎可分为液滴扁平化和剪切剥离两个阶段.其中液滴扁平化是前后驻点高压区和赤道周围低压区的压力差所导致的,而剪切剥离的产生原因是流动分离导致液滴背风面形成漩涡结构.另外可以发现在激波驱动下液滴从球形主液滴破碎为小的子液滴会经历多个循环重复的破碎阶段,这种逐次的循环破碎行为可能和变形后液滴的涡脱落有关.模拟结果也表明不同马赫数下激波冲击液滴所导致的变形和加速特征具有相似性.液滴的变形阶段都遵循具有上述特征的SIE 破碎机制,而液滴的加速过程均展现出了非恒定的运动规律.在前期液滴横向直径变化不大的情况下,液滴可看作刚体以一个恒定的加速度运动,随着液滴扁平化的发生,液滴的加速度也随之增大.基于本文工作,未来研究将考虑极高马赫数条件下液滴周围空气非平衡效应(比如)对激波诱导液滴变形破碎产生的影响.