分段履带式水陆两栖车减阻增速试验及数值仿真*

孙承亮，徐小军，唐源江，郝 军

(1. 国防科技大学 智能科学学院， 湖南 长沙 410073； 2. 重庆长安工业(集团)有限责任公司， 重庆 401120)

水陆两栖车是一种既能在陆地上行驶又能在水上航行的特种车辆，传统的水陆两栖车通常采用轮式或履带式陆上行驶方式，并依靠螺旋桨或喷水推进实现水上航行，在登陆和跨海作战中发挥着重要作用[1]。考虑到水陆两栖车的陆上行驶性能和通过性，水陆两栖车的外形不会像船舶一样具有较好的线型，大多为方形的钝体结构，其流线型较差，水上航行阻力较大，是制约水上航速提高的重要因素。

水上快速性是评价水陆两栖车辆战技性能的重要指标，而减阻增速是提高快速性最有效的途径之一。目前船舶上常用的减阻方法主要是船体线型优化和加装附件。Huang和Yang[2]通过定义目标函数和约束条件，构建了代理模型，得到了最优船体线型。而安装附件是在不改变船舶结构的情况下提高船舶阻力性能的一种简单方法，在高速船舶中广泛采用。

尾翼板是一块从艉部安装向后倾斜的平板，在船舶上得到广泛的应用[3-4]。美国海军在进行了大量的试验研究后，将尾翼板应用在28艘驱逐舰上来提高快速性[5]。Robin等[6]通过仿真和试验研究，认为安装在驳船上的尾翼板可以将兴波能量降低一半，从而减少对河岸的破坏。Maki 等[7]通过模型试验和计算流体力学 (computational fluid dynamics, CFD)研究了压浪板对阻力和航行姿态(包括纵倾和升沉)的影响，结果表明安装压浪板后兴波阻力减小。Villa等[8]通过数值仿真分别研究了安装尾翼板和截流板的滑行艇水动力性能，并建立了尾翼板角度和截流板等效高度之间的关系。Tsai等[9]采用试验方法研究了尾翼板及其与其他附件的组合对滑行艇阻力性能的影响。结果表明，在体积弗劳德数大于3时，尾翼板比其他附件具有更好的减阻效果。Parsons等[10]建立了舰船尾翼的设计模型，可以对尾翼的初步设计参数进行多准则优化。剧冬梅等[11-12]研究了纵倾角对轮式水陆两栖车的阻力特性影响，并设计可收放悬架来减小水上航行阻力，研究结果表明:适当控制水陆两栖车的纵倾角，并对可收放悬架进行参数优化，可以减小阻力。彭锟等[13-14]基于代理模型展开了水陆两栖车外形减阻优化方法研究，并得到了车体最优长宽比、最优航行倾角等水陆两栖车参数。赵彬等[15]采用混合耦合算法和重叠网格技术研究了水陆两栖车的航态变化，仿真结果与试验具有较好的一致性，随着车辆航速的增加，动升力所占比重增大，浮力减小。崔金一等[16-17]对水陆两栖车的结构参数进行了优化，并设计了可收放悬架机构，进行了水上陆上性能仿真，取得了较理想的试验结果。王少新等[18-19]设计了双车厢的水陆两栖车，通过数值仿真和重叠网格技术研究了两车厢各自的水动力特性和球铰链接的影响，并且还研究了不同航速下防浪板的受力特性。

综上所述，近年来国内外针对尾翼板和水陆两栖车的水动力性能展开了大量研究，并且已有部分学者将尾翼板应用在两栖车上的减阻增速上。以往的研究主要集中在尾翼板引起的阻力变化上，对尾翼板长度或安装角度的研究较少。此外，很少有研究从阻力成分和尾流场的角度解释减阻的机理。针对这些问题，本研究以某分段履带式水陆两栖车为研究目标，利用水池拖曳试验和数值仿真相结合的方法，首先通过适当调节重心的纵向位置来减小航行阻力，然后研究了尾翼板的长度和安装角度对车辆阻力的影响。通过分析阻力成分和尾流的变化趋势，解释了减阻机理。

1 几何模型及参数

水陆两栖车的几何模型如图1所示。当两栖车在水上航行时，为减小水阻力会将分段式履带收起，为了方便计算，这里将其简化为等体积的柱形。水陆两栖车的主要参数见表1。

图1 分段履带式水陆两栖车简化模型Fig.1 Simplified geometric model of the segmented-track amphibious vehicle

表1 水陆两栖车主尺度参数

边界层厚度对尾翼板产生的升力有很大的影响。Day和Schlichting等[20-21]提出了一种方法，将船体简化为相同长度的平板来计算边界层厚度：

(1)

(2)

其中，δ(x)是边界层厚度，Rex是雷诺数，ρ为20 ℃下水的密度，V0是车辆的航行速度，μ是20 ℃下水的运动黏性系数。

2 数值计算方法

2.1 控制方程

对于不可压缩牛顿流体的运动，需要满足连续性方程及动量守恒方程：

(3)

(4)

2.2 湍流模型及自由液面

目前工程计算中存在多种湍流模型，不同的模型针对的主要问题不同，因此在计算时需要选取合适的湍流模型。剪切应力传输(shear stress transfer, SST)k-ω模型两方程模型在近壁区保留了原始的k-ω模型，在远离壁面的地方应用了k-ε模型，兼具两者的优势，能够较好地模拟黏性绕流场的细节[22-23]，因此这里选择该湍流模型进行计算。

利用流体体积函数(volume of fluid, VOF)模型追踪自由液面的变化。该方法将每个控制单元中水(或空气)的体积分数表示为αw(或αa)，对于该体积分数，存在3种情况：

1)αw=0，该控制单元中没有水(只有空气)；

2)αw=1，该控制单元中只有水(没有空气)；

3)0<αw<1，该控制单元中存在自由液面，它们之间满足下列方程：

(5)

2.3 边界条件和网格划分

考虑到模型的对称性，取一半进行计算，建立如图 2所示计算域。计算域大小设置为：入口距离车首L(L为垂线间长Lpp), 出口距离车尾3L, 中纵剖面距离侧边1.5L,高为3L。入口、顶部、底部及侧边界设置为速度入口(速度大小为两栖车的航行速度)，出口为压力出口，中纵剖面为对称平面，两栖车表面为非滑移壁面。

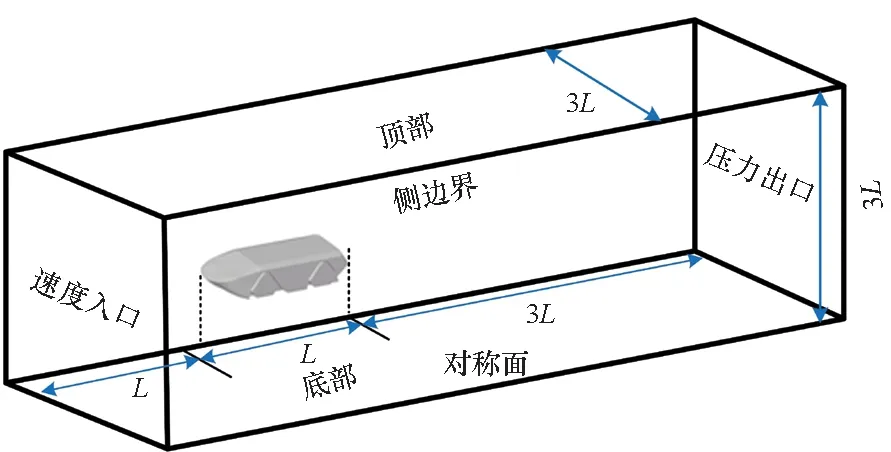
图2 计算域及边界条件Fig.2 Computational domain and boundary conditions

利用CFD商用软件STAR-CCM+ 13.02.011进行网格划分，并对开尔文波区、艏艉等区域加密，生成高质量的切割体网格和棱柱层网格，边界层厚度通过方程(1)计算得到。网格划分总体效果如图3所示。

(a) 开尔文波系(a) Kevin wave system

为了模拟水陆两栖车的真实运动，需要释放2个自由度(2 degree of freedom, 2DOF):即纵摇和垂荡，两者的大小分别用纵倾值和升沉值表示。另外4个自由度即纵荡、横荡、横摇和首摇需要锁定。为达到上述目标，应用流水-刚体相互作用(dynamic fluid body interaction, DFBI)旋转平移模型，将沿Z轴平移和绕Y轴旋转分别释放，限制沿X轴平移、Y轴平移、绕X轴旋转和Y轴旋转。

3 水池拖曳试验

按照1/2.5的缩尺比制作了水陆两栖车的模型，模型实物图如图 4所示。模型表面经防水、喷漆处理，符合“CB/Z 244-88滑行艇模型阻力测试方法”中规定的允许误差标准。拖曳试验在某标准化拖曳试验中进行(见图5)，该水池长510 m，宽6.5 m，水深5 m，采用数字化直流调速系统，拖车速度为0.1～22.0 m/s，车速稳定精度优于0.2%。

图4 水陆两栖车缩比模型Fig.4 Scaled model of amphibious vehicle

图5 水陆两栖车拖曳试验Fig.5 Model towed test of amphibious vehicle

4 结果验证与分析

4.1 网格不确定性验证

在黏性不可压缩流的数值计算中，需要对网格不确定性进行验证，这里选取车速V=2 m/s的阻力系数计算结果进行验证，阻力系数Ct的试验值为4.742×10-2，设置4种不同尺寸的网格，结果如表2所示。

表2 网格不确定性验证

阻力系数的表达式为：

(6)

式中，Rt为两栖车的总阻力。从表2中可以看出，对于中网格，网格数量和计算精度都可以接受，因此这里选择该网格尺寸进行后续计算。

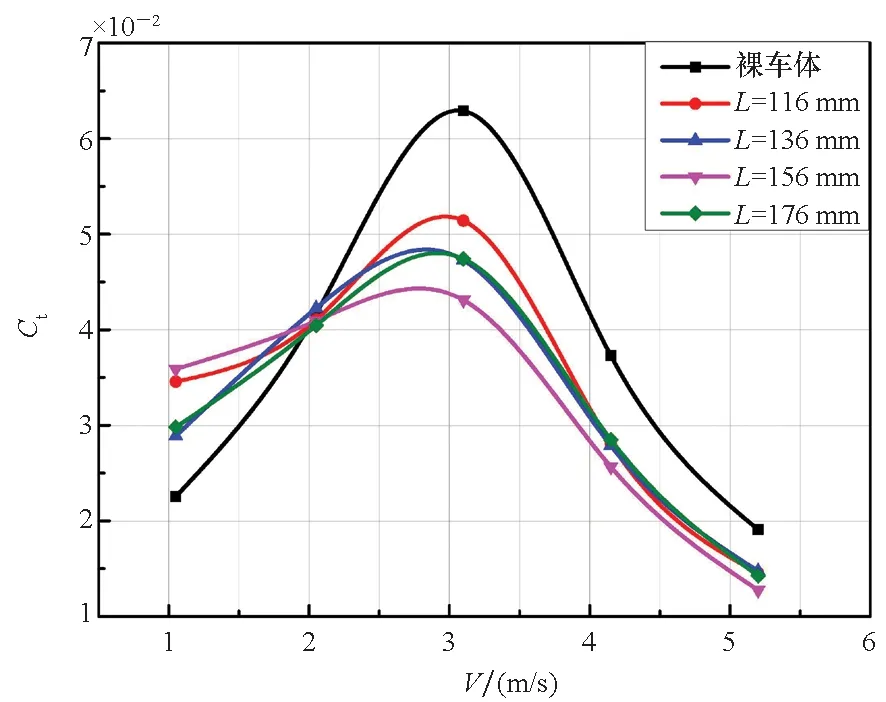
图6给出了试验和数值计算得到的阻力、纵倾和升沉结果。从图6中可以看出，在1 m/s

(a) 阻力变化曲线(a) Change curve of resistance

4.2 车辆纵向重心位置对阻力的影响

以车辆前轴的中点为原点，指向车尾位置为正定义纵向坐标轴，研究重心的X轴坐标值变化对两栖车阻力性能的影响。通过拖曳试验测得了重心在X=480 mm、508 mm、540 mm处的两栖车阻力和姿态变化，结果如图7所示。从图7中可以看出，当速度达到3.5 m/s左右时，阻力开始下降，这是因为随着速度的提高，动升力逐渐增大，车体被抬升开始进入滑行状态，湿面积减小，从而所受阻力减小。比较3条曲线可以发现：当V<4 m/s时，前置重心的车辆，阻力最小；当V>4 m/s时，情况正好相反。

图7 不同重心的两栖车阻力变化曲线Fig.7 Resistance curve of amphibious vehicle with different center of gravity

为了得到高速航行下的重心最佳位置，在上述试验的基础上，利用CFD研究了X=480～600 mm之间变化(间隔20 mm)时，两栖车的阻力变化情况，如图8所示。从图8中可以看出，在5.25 m/s速度下，随着重心的后移，阻力先减小后增加，在X=540～560 mm之间时，阻力最小。

图8 阻力随重心位置变化趋势(V=5.25 m/s)Fig.8 Change trend of resistance with the position of center of gravity (V= 5.25 m/s)

4.3 尾翼板参数对阻力的影响

4.3.1 尾翼板角度

尾翼板与水平面之间的夹角θ会影响两栖车的阻力性能。本文利用CFD研究了尾翼板长度为L=136 mm,θ为0°、5°、10°、15°时阻力系数随速度的变化趋势，如图9所示。从图9中可以看出：当V=3 m/s左右时，相比裸车体，θ=10°和θ=15°的尾翼板减阻率最大，在30%左右；当V=1 m/s时，尾翼板并不能起到减阻的效果，相反会增大阻力。这说明水陆两栖车在低速航行时，摩擦阻力占比较大。

图9 不同尾翼板角度下两栖车阻力曲线Fig.9 Resistance curve of amphibious vehicle with different stern angle

由图9可知，当2 m/s

图10所示为总阻力、摩擦阻力和剩余阻力的减阻率分析。其中，Et表示总阻力的减阻率，Ef和Er分别表示摩擦阻力和剩余阻力的减阻率，其表达式分别为：

(7)

式中，ΔRt、ΔRf、ΔRr分别为总阻力、摩擦阻力、剩余阻力相对裸车的减小值。从图10中可以看出，当3 m/s

图10 阻力成分减阻率分析(θ=10°，L=136 mm)Fig.10 Component analysis of resistance reduction rate (θ=10°，L=136 mm)

4.3.2 尾翼板长度

根据上述分析结果，取θ=10°，尾翼板长度L为116 mm、136 mm、156 mm、176 mm来研究两栖车阻力的变化规律。图11所示为安装有不同长度尾翼板的两栖车阻力变化图。从图11中可以看出，当V>2 m/s时，尾翼板才起到减阻的效果，这与4.3.1节的结论是一致的。当3 m/s

图11 不同尾翼板长度下两栖车阻力曲线Fig.11 Resistance curve of amphibious vehicle with different length

图12给出了各阻力成分的减阻率分析，可以看到3 m/s

图12 阻力成分减阻率分析(θ=10°，L=156 mm)Fig.12 Component analysis of resistance reduction rate(θ=10°，L=156 mm)

图13所示为水陆两栖车周围水面兴波高度图。从图中可以看出，经过重心调节、尾翼板参数优化后，车体中部、艉部的兴波高度明显减小，说明加装尾翼板后，两栖车的兴波阻力减小了。这与上述阻力成分的分析结论是一致的。

图13 自由液面兴波高度Fig.13 Wave height of free surface

方艉是水面高速舰船普遍采用的结构形式，它可以减少高速水流的扭转和弯曲程度，从而减少能量损失，改善阻力性能。如图14所示，高速水流一直延伸到艉部后一段距离处，形成一个中空区，其作用相当于增加了车体的有效长度，但未增加摩擦力，该效应称为虚长度效应。

图14 虚长度示意Fig.14 Virtual length diagram

本研究采用“方艉+尾翼板”相结合的方法，目的在于吸取两者的优点，在更大程度上实现减阻增速。如图15所示，相比原裸车体，加装尾翼板后的两栖车“鸡尾流”现象得到明显的改善，且增强了虚长度效应，从而实现了减阻。

图15 有无尾翼板的方艉处波浪情况Fig.15 Wave condition at stern with or without stern flap

5 结论

本文基于水池拖曳试验和数值仿真相结合的方法，针对某分段履带式水陆两栖车的减阻增速，研究了车体重心纵向位置和尾翼板角度、长度对阻力性能的影响。得出如下主要结论：

1)适当调节重心纵向位置可以实现水陆两栖车的减阻，在模型最高速度V=5.25 m/s(实车V=30 km/h)下，最佳重心位置为X=540～560 mm。

2)尾翼板的安装可以实现较明显的减阻效果，在θ=10°，L=156 mm时，减阻效果最显著，最大减阻率为34.3%。

3)剩余阻力在总阻力中占比较大，摩擦阻力占比较小。剩余阻力在减阻中起主导作用，其减阻率占总阻力减阻率的90%以上。