λ-演算归约策略的简易建模

阿力木江·亚森，阿布都克力木·阿布力孜，朱义鑫，哈里旦木·阿布都克里木

(新疆财经大学 信息管理学院，新疆 乌鲁木齐 830012)

0 引 言

编程语言理论中的计算过程主要包括函数定义、函数调用以及函数调用的归约。几十年来，研究人员一直在研究如何定义函数以及对其调用。以提高效率为目标的计算技术可用于开发函数式编程语言或逻辑编程语言，具有简单推理特点的计算技术可用于建模原型语言。已有的基于图形的计算技术不适用于对形式系统进行推理证明。无类型λ-演算被认为是最小的编程语言，因此以无类型λ-演算为例回顾基于图形的计算技术。

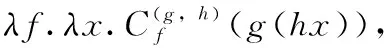
本文以经典λ-演算为例实现函数式编程语言和逻辑编程语言中常用的归约策略的建模。其中λ-表达式以超图表示，超图由结点、普通边和超级边组成的超图。使用超图表示λ-表达式的想法提出在文献[12]中，但其在HyperLMNtal里并没有实现相关开发。文献[13]的图形类型在HyperLMNtal里实现。用超图表示的λ-表达式极为相似于理论上的λ-表达式。该技术使用超图重写的建模语言HyperLMNtal，其中的重写规则能够通过图形类型处理任意大小的子图。

1 HyperLMNtal

HyperLMNtal是基于超图重写的建模语言。程序中的超图按以下语法表达

其中，0是空的超图，p(X1,…,Xm) 是一个名称为p并且具有m个边的结点，P,P是超图的并行组成。Xi可以是最多能连接两个结点的普通边，也可以是连结任意数量的结点的超级边。在程序中，结点名以小写字母开头，边名以大写字母开头。一个超级边被创建时，一个自然数可以作为属性提供给它。特殊结点“=”称为连机结点，用于连接两条边。例如，X=Y连接X的一个端点和Y的一个端点：如果X是普通边而Y是超级边，则X将成为超级边Y的一部分。为了方便地编写程序，该语言提供一种术语表示法，它允许将q(…,Y,…)，p(…,Y) 写为q(…,p(…),…)， 其中Y必须是普通边。对于两条普通边X和Y而言，X=Y，p(…,Y) 相当于p(…,X)， 也可以写为X=p(…)。 利用该术语表达法可编写具有良好可读性的程序。

init.

第一行中给出的结点init将被第二行中的重写规则转换为由3个结点a,b,c以及一条属性为1的超级边K组成的一个超图。一条边在规则左侧和右侧出现的数目可能表示该条边代表的子图正在被删除或复制，如下所述。

边L在第一条规则中被复制，因为L在该规则的左侧出现一次，而在右侧出现两次。显然，边L在第二条规则中被删除。不过这些规则没指出边L代表什么，因此这些规则是无法运行。需要在规则中使用图形类型来说明被复制或删除的每一条边代表什么。图形类型检查给定参数是否具有该图形类型所预期的属性。例如，hlink(L,1)检查L是否为具有属性1的超级边，int(K)检查K是否连接到包含一个整数的结点。除了检查单个图形元素之外，有些图形类型，如ground可用于定义子图。

图形类型ground(L,a1,…,an) 表示通过下面的方法从超图G中获得的子图P={N,E,H}：

从L出发遍历G；

仅遍历普通边并访问结点，而不遍历超级边；

从而获得已被遍历的普通边集合E，已被访问的结点集合N，以及所有端点都在N中并且属性在 {a1,…,an} 中的超级边集合H。

一条超级边K∈H称为P的局部超级边，只有部分端点在P中出现的超级边称为P的全局超级边。简而言之，一个ground是一个由一组普通边、一组结点和一组完全包含在这些普通边和结点之内并且具有指定属性的超级边组成的子图。在重写规则中使用ground可以复制或删除子图，如下所示

init.

第一行给出结点init。第二行中的规则将init重写为r(abs(X,app(X,Y)))，其中r,abs和app是由属性为1和2的超级边X和Y以及一些普通边连接的结点，如图1(a)所示。根据术语表示法，普通边在程序中隐式的，例如r和abs之间是普通边，还有abs和app之间的也是普通边。在图中直线表示普通边，带曲线的黑点表示超级边，箭头指向结点的第一条边表示结点中边的顺序。当在第三行的规则应用于图1(a)中的超图时，ground(L,1)先找到一个子图(图1(a)中的虚线区域)，然后将该子图复制到两个位置，从而获得图1(b)所示的超图。当第四行的规则应用于图1(a)中的超图时ground(L,1)子图将被删除，结果为图1(c)。复制ground子图时，其局部超级边将被复制到新的超级边中，并且全局超级边将在复制后的子图之间共享，例如图1(b)所示图1(a)中的X1被复制到F1和K1，而Y2被共享。删除ground子图时，其局部超级边将被完全删除，并且全局超级边中连结到子图的部分被删除，如图1(c)所示。复制或者删除ground子图时，其中的普通边将被复制到新的普通边中或被完全删除。

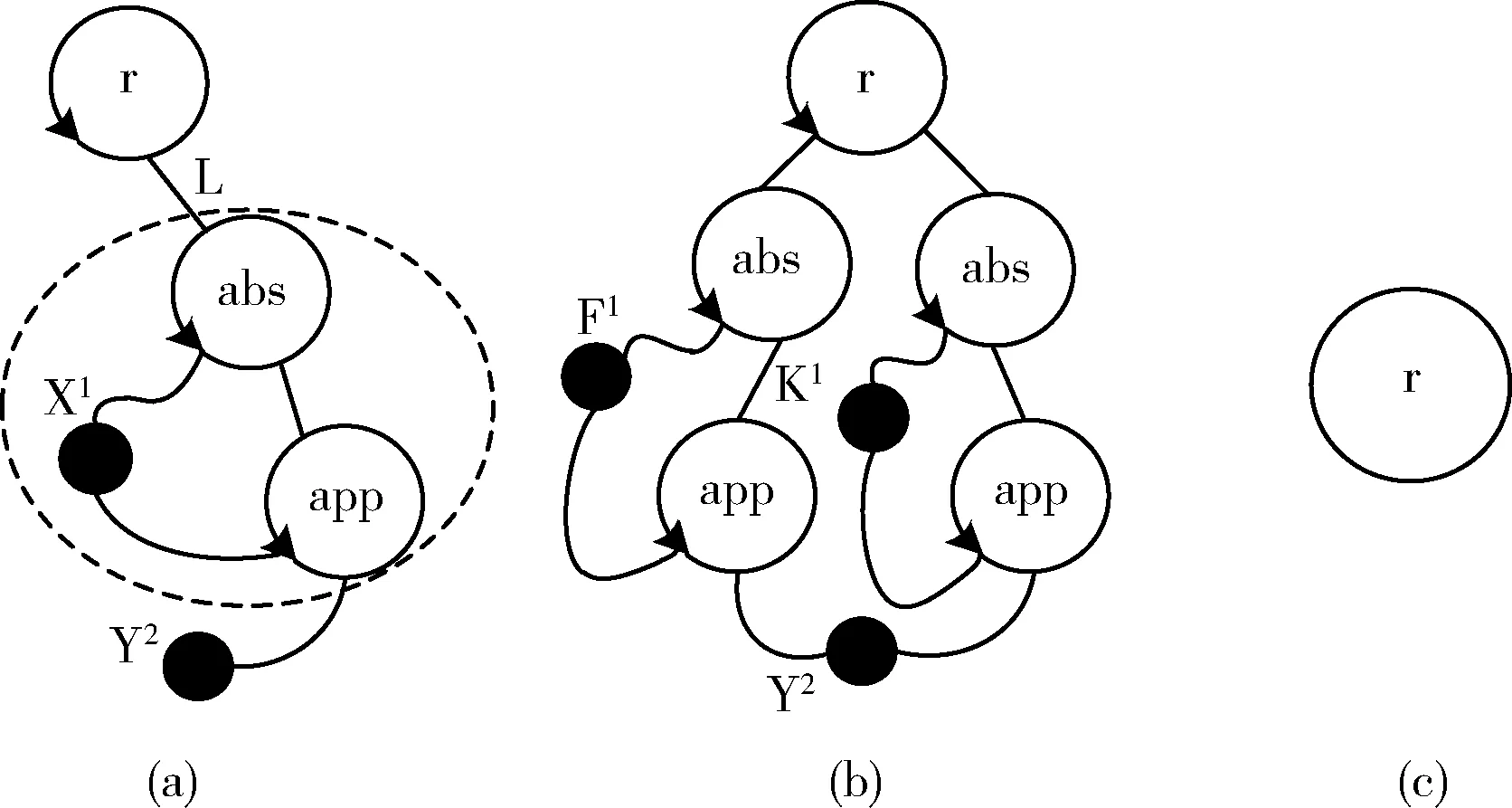
图1 子图的复制与删除

2 λ-演算及其超图表示

2.1 λ-演算

无类型λ-表达式的语法如下

其中x是变量，λx.t是抽象表达式，tu表示将t应用于u的应用表达式。在λx.t中，λx是绑定机制，并称t为λx的辖域，x称为绑定变量，一个未收到绑定并出现在t中的变量称为自由变量。例如，λx.xy中x是一个绑定变量，y是一个自由变量。绑定变量的名称并不重要，λx.x和λy.y是等价的，称为α-等价性。形式为(λx.t)u的表达式称为可归约表达式，通过以下的β-归约法进行归约

2.2 λ-表达式的超图表示

用超图表示λ-表达式既简单又自然。通过应用以下规则可以写出任何一个λ-表达式的超图表达式。

变量：属性为1的超级边表示绑定变量，属性为2的超级边表示自由变量。

抽象表达式：结点abs(X,T,L) 表示λx.t，其中X是表示绑定变量的超级边，T是t的超图表达式，L是普通边。

应用表达式：结点app(T,U,L) 表示tu，其中T和U分别是t和u的超图表达式，L是普通边。

新时代背景下，城市化的发展也进入了一个新的阶段，新时期对于城市规划的要求自然也进一步提高。自然环境保护力度加大，人性化的规划需求的加强以及其他方面的综合因素，要求必须从我国实际情况出发来对城市进行综合、科学和可持续的规划建设。

备注：普通边仅用于通过表示结点之间的父子关系，以形成λ-表达式的框架，而不用于表示变量。

λ-表达式的这种超图表示称为超图λ-表达式。以下程序说明如何使用超图λ-表达式

init.

第二行生成λx.xx的超图λ-表达式，第三行生成λx.x的超图λ-表达式。第四行生成一个将第二行生成的超图λ-表达式应用到第三行生成的超图λ-表达式上所得到的超图λ-表达式。在程序的最后三行中生成的超图λ-表达式分别在图2(a)～2(c)所示。

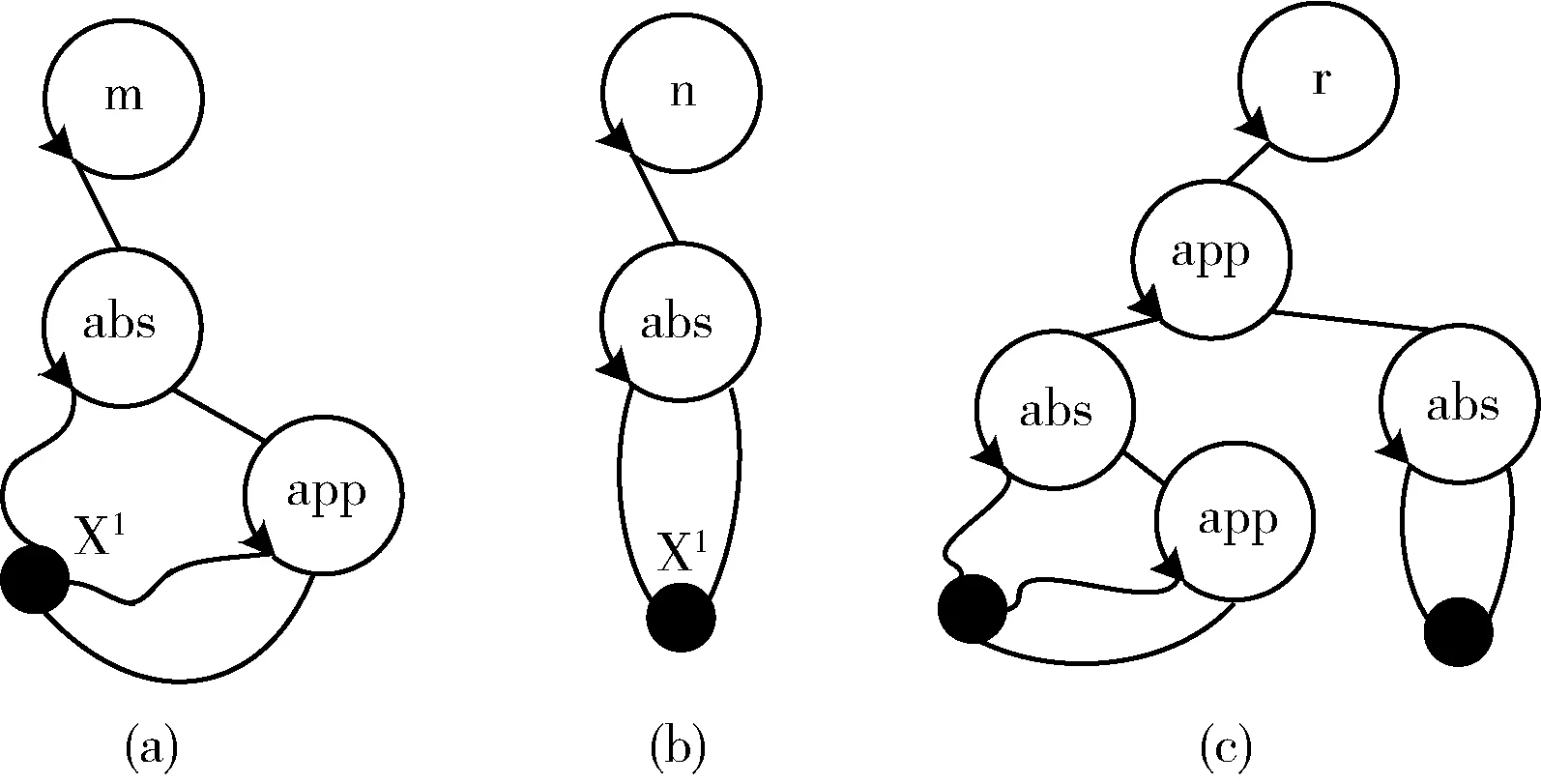
图2 超图λ-表达式

在图形中只要两个不同的名称标记两个不同的边即可，边的名称并不重要。边的这种特性与λ-表达式中的绑定变量的特性完全相同：一个绑定变量可以有任何名称，只要该名称不与其它变量名称发生冲突即可。根据在2.1节中的λ-表达式的语法，可能会有一些令人困惑的λ-表达式如λx.λx.x。在λx.λx.x中，两个绑定变量x不是相同的变量，该表达式实际上相当于λy.λx.x。对于这种不同绑定变量具有相同名称的λ-表达式应转换为不同绑定变量具有不同名称的等价λ-表达式，然后将其转换为对应的超图λ-表达式。此条件也适用于基于图形的其它技术。

3 归约策略的建模

3.1 完全归约

本节介绍超图λ-表达式完全归约的超图重写规则实现。完全规约在任何时间对任何位置的可归约表达式都可以进行归约，该过程一直进行到没有余下的可归约表达式为止。例如，令id=λx.x， 则λ-表达式id(id(λz.idz)) 有3个可归约表达式，它们按任何顺序计算都有相同的结果λz.z，其不包含任何可归约表达式。

表1 避免变量捕获的代换操作定义

ground(T,1) | R=Y.

|R=app(subs(T,X,U),

subs(S,X,U)).

这些规则实现超图λ-表达式的完全归约，由于以下原因其计算过程中绝不发生变量捕获并输出正确的计算结果。第一，第一条规则将自动应用于输入表达式中的任意一个可归约表达式，不存在可归约表达式时停止，这正是完全归约。第二，第五条规则将一个超图λ-表达式复制到它的两个等价并且不同的副本中，从而使所有表示绑定变量的超级边在计算过程中保持不同。在此过程中，表示自由变量的超级边在副本之间共享，这正是λ-演算中自由变量从不更名的情况。第三， ground(L,1) 是一个子图，它由普通边、结点和局部超级边组成，其中普通边和结点组成基本框架。不难发现，ground子图的结构特性与超图λ-表达式的结构特性完全相同。这意味着，在第三条规则中通过ground删除的超图λ-表达式T正是对应于表1中的第二条规则中被删除的λ-表达式t。类似地，在第五条规则中通过ground复制的超图λ-表达式U正是对应于在表1中的第四条规则中被复制的λ-表达式u。

3.2 按名称调用

在完全归约中不存在计算策略，随时可以归约任何一个可归约表达式。完全归约的时间效率低，因此实际编程语言采用其它的归约方式，例如按名称调用归约方式。下面的示例说明如何根据按名称调用进行归约

id(id(λz.id z))

→id(λz.id z)

→λz.idz

按名称调用总是试图归约最左最外面的可归约表达式(归约下划线的表达式)，并且不允许在抽象表达式内部进行归约。例如，在上面第三行不计算λz的辖域里面的可归约表达式，最终结果为λz.idz。

为了实现这种按一定顺序进行的归约方式，将引入两个节点。结点eval包装一个输入表达式，并开始对该表达式进行归约。结点value将抽象表达式标记为值，它防止在抽象表达式之内进行归约。下面的一组重写规则实现按名称调用归约方式

init.

|R=abs(X, abs(Y, app(X,app(X,Y)))).

其中，第二行中的规则产生一个将丘奇数1应用到丘奇数2的应用表达式，该表达式通过最后三行实现按名称调用方式进行归约。如在第六行规则所示，当eval遇到一个应用表达式时首先尝试归约其左侧。如在第七行规则所示，当eval遇到一个抽象表达式时，将用value将该抽象表达式标记为值，因此不会在抽象表达式内进行归约。当一个可归约表达式的左侧参数已标记为value时，最后一行的规则触发β-归约并产生代换表达式，该代换表达式将由3.1节中实现的代换操作的4条规则来计算。

在3.1节中的完全归约的重写规则中只要存在可归约表达式就将触发β-归约，没有特定的归约顺序。只要存在可归约表达式，HyperLMNtal自动调用β-归约法的重写规则。在按名称调用的归约方式中，3个规则利用eval和value遍历一个表达式并根据按名称调用的原理控制归约顺序。

3.3 按值调用

大多数编程语言使用按值调用归约。与按名称调用不同，按值调用计算右侧已成为值的可归约表达式，如以下示例所示

id(id(λz.id z))

→id(λz.id z)

→λz.idz

为了归约第一行中最外面的可归约表达式，首先应该归约其右侧(下划线的表达式)。在第二行中可以归约最外面的可归约表达式，因为其右侧已经归约为值。简而言之，按值调用归约一个可归约表达式之前，首先需要归约其左侧和右侧部分。以下重写规则实现按值调用

第一条规则将抽象表达式标记为值。第二和第三条规则按从左到右的顺序归约一个可归约表达式的左侧和右侧。当一个可归约表达式的两侧部分都归约为值时，第四条规则触发β-归约并产生代换表达式，其由3.1节中实现的代换操作的4条规则来计算。按这些规则所计算的输入表达式的构造方法在3.2节中已经给出。

上述介绍的按名称调用和按值调用的重写规则不能计算包含自由变量的表达式。通过在按名称调用和按值调用的重写规则中添加以下处理自由变量的重写规则，使它们能够计算包含自由变量的表达式

以上规则的作用是将自由变量的不可归约表达式标识为值。例如，第一条规则将一个自由变量标识为值。第二条规则将一个左侧为值的应用表达式标识为值，其中左侧本来是一个自由变量。第三条规则中将左侧已标识为值的应用表达式标识为值，其中左侧是一个应用表达式。

3.4 模型分析

本文所提出的技术与其它基于图形的技术不同之处在于以下几点。第一，已有的基于图形的技术使用普通边和某些辅助结点来表示变量。在本文所给出的技术中，超级边能够表示任何变量，并不需要额外的结点来表示出现次数多于2的变量。第二，大多数基于图形的技术都是用Interaction Nets，其中重写规则每一次只能更改几个基本图形元素，不能处理任意大小的子图。本文所给出的技术中，重写规则使用图形类型可以重写任意大小的超图λ-表达式，因此各种归约策略的重写规则实现简单而紧凑，几乎与理论完全一致。第三，在大多数基于图形的技术中，对λ-表达式归约策略建模时需要一组专门的重写规则来实现资源管理。本文所给出的技术不需要在计算过程中专门清理不再需要的表达式的重写规则，不再需要的表达式在实现代换操作的重写规则中由ground立即删除即可。第四，文献[14]提出使用辅助结点来遍历图并限制归约顺序的方法，并将该方法用在普通图形重写中。本文提出的技术将使用辅助结点来遍历图的思路引入到超图重写中。

4 结束语

本文介绍了一种基于超图重写的实现各种归约策略的技术。在该技术中，超图λ-表达式在形式上相似于理论中的λ-表达式并且具有良好的可读性。归约策略用超图重写规则实现，其中使用的图形类型ground执行显式α-转换。完全归约、按名称调用和按值调用的重写规则易于理解，并且对计算过程的描述完全对应于理论上的描述。该技术中，限制归约顺序的方法被融入到超图重写中，因此能够直观地实现各种归约策略。如在引言中指出，大多数基于图形的技术是为了高效计算。本研究没有优先考虑计算效率，而认为与理论相似程度的高低和是否能获得直观的计算模型才是优先考虑。该技术可用于快速建模和演示。例如，如果在实际开发某一个形式系统之前想要测试或者演示它，那么该技术可用于建立它的可执行模型。另外，由于使用该技术时理论和实践几乎保持一致，因此，这种建模过程将是比较简单的。将来的研究方向是进一步提高该技术的计算效率，以期能应用到更复杂的大型形式系统中。