考虑AGV路径规划的智能制造流水线车间布局研究

毕 娜

(浙江工业大学 机械工程学院,浙江 杭州 310023)

制造业是国民经济的主体,在当前信息技术高速发展的有利条件下,将制造业向智能化转型是制造业发展的迫切需求。智能制造是新一轮工业革命的核心技术,是“中国制造2025”的主攻方向[1]。在智能化支撑下的制造业,其生产环境将会发生一系列变化。如大量采用了机器人、立库和AGV等智能技术后,其制造全过程的调度需求无疑发生了全方位的改变。因此,新环境下生产系统的车间布置研究变得尤为迫切,通过计算机智能方法对其进行研究,促进智能制造的进一步发展。通过智慧感知获取环境信息和资源状态,实现人、机和物三者的互联互通[2]。在智能制造中,传统的人工叉车搬运物料将逐步被智能化的物料运输方式所代替,如采用AGV进行车间物料运输。全面应用AGV能够大大提高企业的生产效率以及制造系统的灵活性与柔性,从而实现智能制造车间的自动化。因此,制造业从传统模式往数字化、智能化转型的过程中,在新厂建成布局时就应该考虑AGV的最优路径。

有关车间布局的研究已趋于成熟,Hosseini等[3]在设施布局规划时考虑了生产周期和生产率;Suhardini等[4]在设施布局过程中,除了考虑到物流成本最小因素,还考虑了不同作业单位间密切程度的最大化约束;冯定忠等[5]基于U型布局构建了单元制造系统;陈勇等[6]提出了针对一类多态性作业车间的低熵化布局评价指标;陈勇等[7]针对注塑车间建立了单元系统布局与关联优化集成模型;葛晓梅等[8]、马玉莹等[9]以及韩昉等[10]通过改进算法来优化加工车间布局。在现有的研究中,一并考虑AGV最优路径的车间布局研究则相对较少。何永乐[11]在确定设备布局的同时考虑AGV的路径规划对系统总运输量的影响,采用禁忌搜索算法对初始解进行优化以确定回路的最终布局顺序;侯鲁洋[12]构建了涵盖AGV系统多个子问题的综合设计数学模型;刘庄成[13]研究了车间布局与AGV系统的协同设计问题,给出了车间布局与AGV系统整体设计方案;葛华辉等[14]建立了智能制造数字化车间布局和AGV路径规划集成优化模型,并提出了一种改进的带精英策略的快速非支配排序遗传算法。不同产品类型的布置方式在考虑使用AGV时所采用的建模方法和求解方式不同,需要做不同的研究。笔者研究适合产品品种较少但数量较大的生产方式,即带有AGV路径优化的流水线车间布局。流水线车间的各条流水线相对独立,各流水线最后一道工序后续又有一起加工的要求,因此,不能将各流水线进行简单地串联,且每条流水线又无法形成闭环,导致AGV空行程多,研究考虑AGV规划的流水线车间布局以提高车间生产效率。

1 模 型

1.1 问题描述及相关假设

传统流水生产线布局如图1所示。图1中:Mij代表第i条流水线的第j台设备(i=1,2,…,m;j=1,2,…,nm);m代表流水线的条数;ni代表第i条流水线的设备数(i=1,2,…,m);Msp代表各流水线的后续工序。这种布局方式的问题在于:设备之间的物流量都是从前一道工序设备往后一道工序设备进行搬运,当AGV运行到流水线最后一道工序设备再返回到第一道工序设备时,第二批物料搬运的过程都是空行程,造成AGV运行效率低下。

图1 传统流水线布局Fig.1 The layout of flow shop

在按产品布置的流水线智能车间中,为完成一批已知加工顺序工件的加工计划,需要给出流水线车间设备合理布局和AGV路径方案,使车间物料运输总成本最低及AGV路径最短。同一条流水线的设备前后顺序固定,工序固定;不同流水线的位置及相对距离可变。

对智能制造流水线布局作如下假设:1) 有若干条流水线,各生产线的加工顺序一定,各流水线之间的相对布局未知;2) 布局的设备,不考虑其形状,假设均为尺寸大小相同的矩形;3) 设备间物料搬运的优先级相同;4) AGV物料运输路径只能为水平或垂直方向;5) AGV一次运输一批物料;6) 物料存放在各设备的中心;7) 该系统的AGV为单一负载车辆、双向运行。

流水线车间共有m条流水线,每条流水线的设备数量不尽相同,用ni表示,i={1,2,…,m},nmax表示各流水线中设备最多的数量。智能制造流水线设备可选位置如图2所示。图2中:X轴和Y轴分别代表车间的水平方向和垂直方向;提供m行,nmax列,共m×nmax个可选位置;Lij代表第i行第j列的位置,其中i={1,2,…,m},j={1,2,…,nmax}。

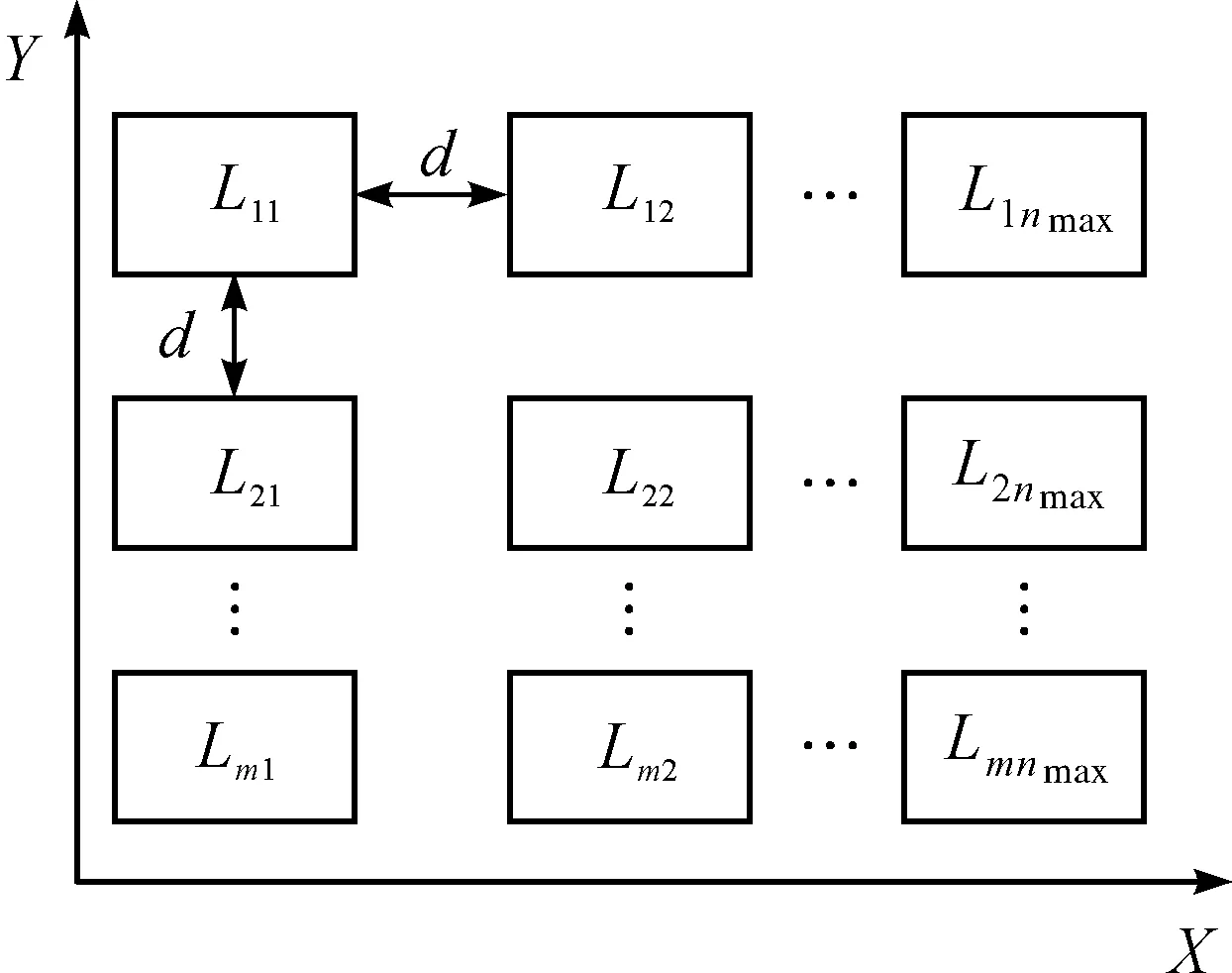
图2 智能制造流水线设备可选位置示意图Fig.2 The available locations of the equipment

考虑到几条流水线的后续工序通常需要把不同流水线的物料集中到一起,应建立一个物料集中区。根据m和nmax的数值特点,物料集中区的位置设置可分为4种情形,如图3所示。图3中的○代表物料集中区,用Mtt表示。当m为偶数,nmax为奇数时,物料集中区的位置如图3(a)所示;当m为奇数,nmax为偶数时,物料集中区的位置如图3(b)所示;当m,nmax均为奇数时,物料集中区的位置如图3(c)所示;当m,nmax均为偶数时,物料集中区的位置如图3(d)所示。各设备之间及设备与物料集中区之间的距离为X方向及Y方向的坐标差值之和。

图3 物料集中区Fig.3 The material collection point

1.2 目标函数

考虑按产品分类的流水线布局,其工艺顺序既定,则车间总物流量为

(1)

式中:fijkl为第i条流水线设备k到第j条流水线设备l之间的物流量;dijkl为第i条流水线设备k到第j条流水线设备l之间的距离;ni为第i条流水线的设备数;m为流水线的条数。由于不同生产线之间无物流量,当i≠j时,fijkl=0;同一条流水线中,只有前后工序设备间有物流量,所以当i=j时,l=k+1。当diik(k+1)最小,F即最小,车间总物流量最小的目标值无法衡量流水线智能车间的布局是否最优。此时,应再设立一个目标,即AGV路径最短。以一条流水线的物流运输使用一台AGV为例,AGV运行一次的路径为

(2)

式中:diik(k+1)为某条流水线相邻工序设备间的距离;dii1ni为首道工序和末道工序设备间的距离;dMiniMtt为第i条流水线最后一道工序设备和物料集中区的距离;ni为第i条流水线的设备数;m为流水线的条数。因为AGV运行为一整条路线,所以运行次数由该条流水线某相邻两道工序间物流量的最大值决定,将这个值视为该条流水线的物流量,其计算式为

Fi=max{fiik(k+1)}
i=1,2,…,m;k=1,2,…,ni-1

(3)

式中fiik(k+1)为某条流水线相邻工序间的物流量。若几条流水线串联成AGV回路,以两条流水线为例,分别为第p条和第q条流水线,则该AGV回路的路径为

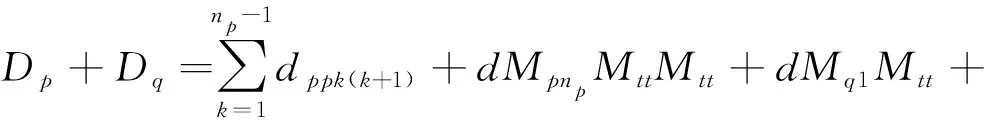
(4)

该条回路的物流量为

Fp=Fq=max{fppk(k+1),fqqk(k+1)}

(5)

所有AGV的最短路径,即目标函数为

(6)

1.3 约束条件

因为几条流水线的后续工序通常需要把不同流水线的物料集中到一起,所以不同的流水线不能简单使用串联的方式来运行。为了使Di最小,需要考虑放弃流水线直线布局,改为环形布局。若各条流水线的物流运输量相对均衡,且均在单台AGV运载能力范围内,则考虑每一条流水线一台AGV。把每条流水线各自布局为环形,并使各条流水线完成最后一道工序的设备尽可能靠近物料集中区。若其中两条或者多条生产线物流运输量较少,则考虑这几条流水线串联成一条回路,现在只研究单台AGV能够负荷几条流水线物流量的情况。

构建一个r×s矩阵,代表r×s个设备可选位置,即

其中:r=m;s=nmax。相邻位置之间的距离记为d,将各条流水线的设备分配到各个位置当中,并满足

diik(k+1)=di=1,2,…,m;k=1,2,…,ni-1

(7)

2 改进遗传算法

为了求解智能制造流水线布局问题,现将交叉算子和变异算子做一定的改进,以此来改进遗传算法。

2.1 编码设计

由于流水线车间布局问题属于多条流水线的位置问题,采用位置编号的编码,长度为位置的数量。车间可以提供r行s列的矩阵,共r×s个位置,每个位置以所在行和列的数字表示。如可以提供3×3个位置,则编码可以为[11,12,13,21,22,23,31,32,33]。

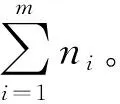
剩余的数字则代表该位置为空位。如车间有3条流水线,第1条流水线有3台设备,第2条和第3条均为2台设备。则M11的位置在L11;M12的位置在L12;M13的位置在L13;M21的位置在L21;M22的位置在L22;M31的位置在L23;M32的位置在L31;L32和L33为空位,没有设备。

2.2 初始种群的产生

因为布局问题的研究对象是流水线车间,所以不能随机产生一个编码,降低运行效率。可以通过将流水线依次排上这种布局方式来产生初始编码,虽然这种方法不能对AGV的路径加以考虑和规划,但是得到的都是可行解。这一部分初始种群可以减小遗传算法的搜索范围,使初始种群能够更广泛地分布,并且能够避免改进后的遗传算法过早陷入局部最优。

2.3 适应度函数和选择操作

选择操作是基于染色体适应度函数值进行的遗传操作。适应度较高的染色体将会以较大概率被选择到下一代,适应度较低的染色体将以较小的概率被选择到下一代。根据问题的实际情况,选择最优保存策略的选择操作。

记录当前种群中适应度最高的染色体Vmin,经过选择、交叉和变异后,若下一代种群中所有染色体的适应度均小于Vmin的适应度,则用Vmin取代下一代种群中适应度最低的染色体[15]。最优保存策略可使得种群中的最优染色体不会由于经过选择、交叉和变异等遗传操作而遭到破坏,其适应度函数如式(1,6)所示。

2.4 交叉操作

由于编码方式的特殊性,因此不能任意选择两个交叉位进行交叉。通过改进临边重组法,建立邻接表来实现交叉操作。先将编码[11,12,13,21,22,23,31,32,33]转变为矩阵:

根据该矩阵中各数据建立邻接表,表示与某个基因值相邻的所有基因。建立的邻接表如表1所示。由表1可知:从确定第1个基因值开始,更新邻接表,依次确定各个基因值。改进后的交叉操作能够较好地保证解的可行性。

表1 邻接表

2.5 变异操作

因为流水线的特殊性,不能随机选取一个基因,将其基因值插入到另一个随机选取的基因位前,会使得求解变得没有效率。改进插入变异法,将整个基因编码,按照流水线的数量,划分为m+1个基因串,其中一个基因串为空位。改进后的变异操作只在某个基因串里进行,选择基因串里的最后一个基因,将其基因值插入到该基因串第1个基因位前。如将编码根据流水线数量划分为[11,12,13,21,22,23,31,32,33],选择第1个基因串进行变异操作,变异操作后的编码为[13,11,12,21,22,23,31,32,33]。

3 算 例

3.1 算例1及其优化

某车间为流水线车间,共有4条流水线,各流水线分别有5,4,4,3组设备,设备之间的物料搬运量如表2所示。根据表2提供的数据,计算出各条流水线物流量相对均衡,采用一条流水线使用一台AGV进行物料搬运的方式。

表2 各设备之间的物料搬运量之情形1

根据式(3)可计算出:F1=max{f11k(k+1)}=max{f1112,f1123,f1134,f1145}=50;F2=50;F3=60;F4=70。车间可以提供5×4=20个位置,相邻位置之间的距离d设定为1,则设备可选的位置和物料集中区如图4所示。

图4 设备可选位置及物料集中区Fig.4 The available locations of the equipmentand the material collection point

采用改进遗传算法对智能制造流水线车间布局问题进行求解,得出解为[13,12,11,21,22,42,41,31,32,43,44,34,33,14,24,23,15,25,35,45],其最优路径值为1 350。算法收敛曲线如图5所示,布局图如图6所示。

图5 算法收敛曲线Fig.5 The algorithm convergence curve

图6 最优解位置分布Fig.6 The location distribution of the optimal solution

3.2 算例2及其优化

某车间为流水线车间,共有4条流水线,各流水线分别有5,4,4,3组设备,各设备间的运输量如表3所示。根据表3提供的数据,计算出各条流水线物流量的差别较大,采用第1条和第2条流水线分别单独使用1台AGV,第3条和第4条流水线公用1台AGV进行物料搬运的方式。由式(3)可计算得出:F1=max{f11k(k+1)}=max{f1112,f1123,f1134,f1145}=70,F2=80;由式(5)可计算得出:F3=F4=max{f33k(k+1),f44k(k+1)}=max{f3312,f3323,f3334,f4412,f4423}=50。车间可以提供5×4=20个位置,相邻位置之间的距离d设为1,设备可选位置和物料集中区仍然如图4所示。采用改进遗传算法对智能制造流水线车间布局问题进行求解,得出解为[12,11,21,31,32,13,14,24,23,44,45,35,34,42,43,33,15,25,22,41],其最优路径值为1 630。算法收敛曲线如图7所示,布局图如图8所示。

表3 各设备之间的物料搬运量之情形2

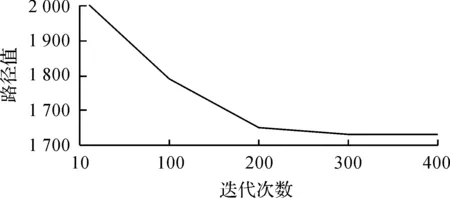
图7 算法收敛曲线Fig.7 The algorithm convergence curve

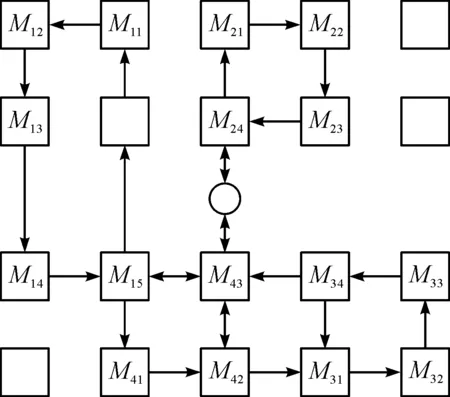
图8 最优解位置分布Fig.8 The location distribution of the optimal solution

3.3 方法比较

比较成熟的方法是先对智能制造流水线车间的设备布局进行规划,再对AGV路径进行优化。根据上述2个算例,将其与笔者方法进行对比验证。算例1中,首先以物流量最小为优化目标;然后使各流水线最后一道工序尽量靠近下一道工序,得到优化的设备布局为[11,12,13,14,15,42,43,44,45,22,23,24,25,33,34,35,21,31,32,41];最后优化AGV路径,得到路径值为2 290。算例2中,得到优化的设备布局为[21,22,23,24,25,32,33,34,35,12,13,14,15,43,44,45,11,31,41,42],得到的AGV路径优化值为2 380。经对比,笔者方法可行、有效,能较好地提高运输效率,提升生产效率。同时发现,各流水线物流量较均衡的情况下,笔者方法可以使AGV运行效率提升。

4 结 论

提出了一种同时考虑设备布局与AGV路径优化的智能制造流水线车间模型,并采用改进交叉和变异算子的遗传算法对其求解。基于流水线车间的特点,结合AGV路径规划的要求,将各流水线布局设立为环形布局,并使每条流水线最后一道工序设备尽可能靠近物料集中区。改进的遗传算法采用位置编号的编码,长度为位置的数量,改进了交叉算子和变异算子,保证解的可行性。通过算例分析,验证了笔者方法的可行性和有效性。后续的研究将重点考虑AGV路径规划的智能制造车间其他生产方式的设备布局,以适应智能制造大环境下,各类型企业的不同需求。