裂缝宽度对预应力混凝土箱梁承载能力的影响研究
2022-09-30冷涛
冷 涛
(中铁十一局集团第二工程有限公司 湖北十堰 442013)
1 引言
随着我国基建工程的发展,大跨度桥梁越来越多,预应力箱梁由于其良好的结构性能,在桥梁工程中获得了广泛应用[1-2]。邹育麟等[3]通过有限元方法,研究了混凝土箱梁桥的承载性能劣化规律;黄峰等[4]根据实际工程监测数据,研究了温度对混凝土箱梁应力和变形的影响;方圣恩等[5]通过数值模拟手段研究了隔震支座对混凝土箱梁地震易损性的影响;虞子楠等[6]通过足尺寸模型试验,计算了预应力混凝土箱梁损伤后的剩余承载力,并对其变化规律进行了归纳总结;卫俊岭等[7]通过ANSYS软件建立了混凝土连续箱梁桥模型,研究了温度对混凝土桥梁的影响,并通过实测数据验证了该数值模型的有效性;蔺鹏臻等[8]通过有限元方法,对混凝土箱梁的碳化规律进行了研究;宋旭明等[9]通过MIDAS FEA软件模拟了混凝土箱梁的施工步骤,研究了箱梁结构受力状态在不同施工阶段的变化特征。
在预应力混凝土桥梁的日常运营中,裂缝存在是一种普遍现象。为了通过裂缝宽度评估桥梁极限承载力并判定桥梁超载和限载,本文依托实际工程,进行了1∶4的相似模型试验;对截面挠度、混凝土应力应变数据进行了监测,并将实测值与理论计算值进行了对比,获得了合理的修正系数;最后,依据裂缝宽度对桥梁最大承载力进行了评估,根据试验数据,得到了截面承载率与裂缝宽度比的拟合公式。本文的研究成果对实际预应力混凝土桥梁工程的安全评价有一定的参考借鉴意义。
2 模型试验
2.1 工程概况
本文依托大水沟大桥项目,该桥梁为三跨预应力混凝土连续刚构桥,上部结构为预应力混凝土变截面连续刚构,主梁采用单箱单室截面,箱梁顶板横坡通过箱梁左右腹板高度差调节形成。箱梁腹板为直腹板,上部结构施加三向预应力。
模型试验采用相似比1∶4进行设计,顶板宽度设置为3 m,底板宽度设置为1.35 m。桥梁为三跨连续刚构桥,每跨长度等效后为8.25 m,设置横隔板在跨中和端部位置处。边墩支座距离梁端为0.2 m,模型整体长度为25.15 m。图1展示了模型的截面尺寸和配筋情况。箱梁和主墩材料均为C40混凝土,非预应力钢筋型号为HRB335,预应力钢筋在模型中通过钢束替代。表1和表2分别展示了钢筋和混凝土的力学性能指标。

表2 混凝土力学特性
2.2 测点布置
通过预埋式振弦应变计对梁体混凝土应变进行监测,监测位置为跨中截面、边跨1/4截面以及支座截面。通过百分表对梁的竖向挠度进行测定,安装位置为每跨的1/4和3/4的底板位置处以及每跨的L/2截面翼缘板底部,安装方式为对称安装。图2展示了控制截面挠度测点布置情况,图2a为1/4跨和3/4跨截面,图2b为跨中截面。此外,模型支座为球罐型橡胶支座,等级为500 kN。
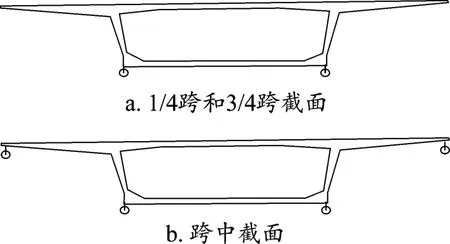
图2 控制截面百分表布置示意
2.3 荷载加载方式
荷载加载方式亦通过相似原理进行确定,结合实际工程情况,以均布荷载的形式施加模型的自重恒载和二期恒载,大小总和为1 100 kN。基于应力等效原则,以集中荷载的方式对车辆活荷载进行替代:

式中,Pp和Pm分别代表实际受到的集中荷载和模型受到的集中荷载;Ap和Am分别表示实际面积和模型面积;σp和σm分别表示受到集中荷载后实际产生的应力和模型产生的应力;Cσ和C1分别为应力相似系数和几何相似系数,依据前人相关研究成果确定相似系数Cσ为1,C1为1/4。
得出集中荷载相似系数Cp为1/16。因此,查阅相关规范后确定模型集中荷载大小为每跨跨中80 kN。
2.4 预应力张拉
模型试验预应力施加方法为后张法,通过穿心式千斤顶对预应力钢束进行张拉,锚具为锥形锚具。通过三弦智能传感器对预应力钢束的应力变化情况进行测量,控制应力0.75fpk=1 400 MPa。表3展示了预应力钢束张拉过程中的应力情况。
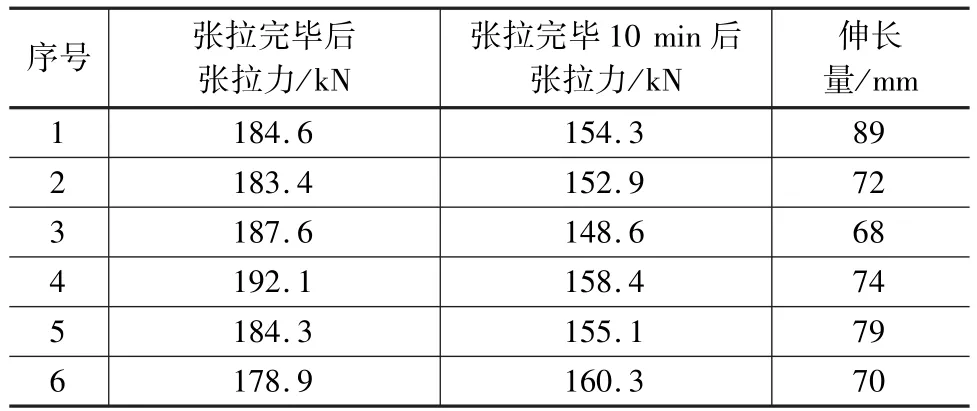
表3 预应力钢束张拉时的基本参数
3 理论计算
在混凝土结构开裂前,预应力混凝土结构变形为弹性变形,开裂后则包含一定的非线性特征。因此,对于混凝土结构的理论计算方法主要有两种,一种为弹性计算方法,一种为非线性计算方法。弹性计算方法较为简便,容易实现,但是往往很难反映混凝土开裂后的变形特征。而非线性计算方法相较于弹性计算方法更接近于实际情况,但是计算较为复杂,且一般是取近似解。
本文建立了预应力混凝土桥梁弹性模型和非弹性模型,以此获得了跨中挠度以及特征截面混凝土应力应变的计算结果,并与试验实测值进行对比分析验证。弹性分析模型是通过梁单元构建的,共有78个节点,75个单元。非弹性模型通过有限元软件建立,由于桥梁为对称结构,因此只需建立1/2模型,单元为实体单元。网格划分后,共13 674个有限元单元。混凝土弹性模量和有效预应力通过表2和表3进行取值。
4 结果与讨论
自重恒载和二期恒载施加完毕后,结构未出现裂缝,仍保持弹性变形状态。直到施加集中荷载共计为300 kN时,混凝土出现开裂,表明该混凝土桥梁的开裂荷载约为正常汽车荷载的1.2倍。
4.1 挠度分析
图3展示了跨中荷载与挠度变化曲线。从图中可以看出,跨中荷载小于300 kN时,荷载-挠度变化曲线呈直线,结构变形为弹性变形。荷载超过300 kN后,混凝土开始发生开裂,荷载-挠度曲线呈现出非线性关系。对比顶板左侧、顶板右侧、底板左侧和底板右侧挠度变化曲线,变化趋势和数值大小均较为接近,可见挠度变化具有极大的相似性,同一截面下随位置变化较小。

图3 跨中荷载与不同位置处挠度变化曲线
表4展示了跨中挠度理论计算结果与实测结果对比情况,理论计算包含弹性计算和非线性计算,而荷载等级则表示正常汽车荷载的倍数。从表4中可以看出,随着荷载等级的增加,梁体的挠度呈现指数增长,荷载等级越大,挠度增加速度越快。与试验实测值相比,弹性计算结果在荷载等级较小时较为接近实测值,而随着荷载等级的增加,误差越来越大。这是由于在荷载等级大于1.2之后,混凝土发生开裂,梁体变形为非线性,导致出现计算结果与实测结果较大偏差。相比于弹性计算,非线性计算更接近于实测值,且并未随着荷载等级增加误差增大,可见混凝土挠度变形主要为非线性,与非线性理论计算结果趋近。将2.0倍以内荷载的弹性分析结果与试验结果进行对比和分析,可以确定若通过弹性分析法对挠度进行估算时,其修正系数建议取1.6~2.0。
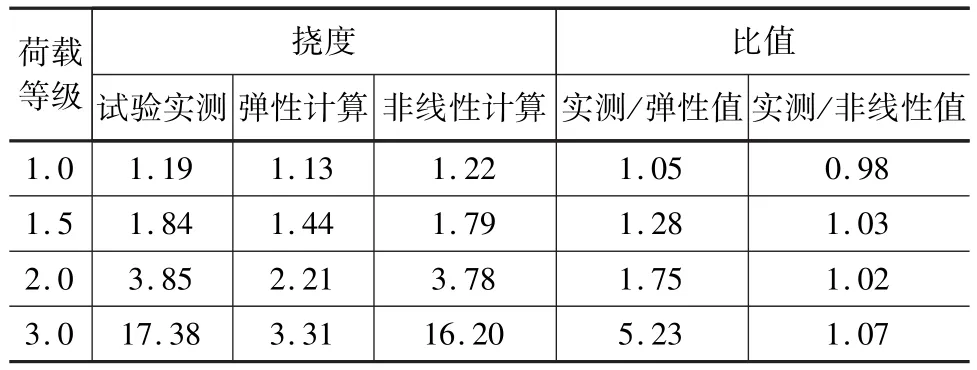
表4 跨中挠度计算结果与实测结果对比
4.2 混凝土应力应变
图4展示了支座处的混凝土应变随荷载变化情况。从图中可以看出,随着荷载的增大,不同位置处混凝土应变均出现不同程度的增加。应变表现最大的为顶板左侧,底板左右两侧混凝土应变大小随荷载变化趋势均较为接近,顶板右侧应变最小。此外,从图中可以看出,顶板左侧混凝土应变在荷载接近500 kN时发生突变,出现大幅增加,这说明在荷载大小为500 kN时混凝土裂缝可能出现贯通,钢筋屈服,导致其应变突然增大。

图4 混凝土应变随荷载变化曲线
表5给出了混凝土应力理论计算结果与实测值的对比情况。从表5中可知,第一跨跨中顶板混凝土应力为负值,底板混凝土为正值,与支座处正负关系恰好相反。在荷载等级较小即混凝土开裂之前时,弹性计算结果以及非线性计算结果与实测值较为吻合。混凝土开裂后,混凝土应力应变状态不遵循线性关系,因此与理论计算误差增大。弹性计算方法与非线性计算方法相比,误差方面两者均未表现出明显优势,但弹性计算方法效率高,易于实现,因此选用弹性计算方法对混凝土开裂后到2.0荷载等级区间的数值拟合,修正系数在1.6~2.5之间。

表5 混凝土应力的理论计算结果与实测值对比
5 基于裂缝宽度对结构承载能力评估
根据相关研究[10],箱梁截面由于构造、截面换算和钢筋布置等方面的差异,使得根据规范公式计算出的裂缝与实际情况存在一定的出入。已有研究表明[11-12],若将箱梁结构截面作为T形或矩形截面考虑无法准确反映其力学行为特性。因此,根据混凝土箱形截面特性,并结合已有研究,系数C3取1.25。
本文依据裂缝宽度对结构承载能力进行了评估,具体实施方法如下:
(1)通过试验,获取各级荷载下截面的实测弯矩M1,依据配筋率计算出极限抗弯承载力Mu,然后算出M1/Mu,即承载率。
(2)令修正系数C3=1.25,依据裂缝宽度计算公式对最大荷载作用下的裂缝宽度Wfk进行计算,然后根据试验结果获取各级荷载作用下的裂缝宽度W1,得出W1/Wfk,即裂缝宽度比。
(3)通过数值方法对承载率和裂缝宽度比之间对应关系进行拟合。
图5展示了截面承载率与裂缝宽度比关系。图5a为跨中截面裂缝宽度比与截面承载率对应关系,图5b为支座截面裂缝宽度比与截面承载率对应关系,图5c为根据试验数据进行拟合得出的曲线。
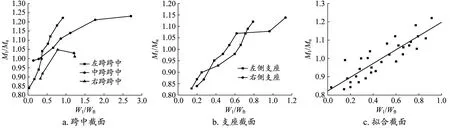
图5 截面承载率与裂缝宽度比关系
观察图5a和图5b可以发现,在裂缝宽度比较小时,截面承载率与裂缝宽度比之间呈现线性关系。随着裂缝的扩大,混凝土变形逐渐向塑性转化,导致截面承载能力随裂缝开展增加速度减缓。裂缝宽度比超过1.0后,截面承载率随裂缝宽度比增加更为缓慢,且表现出了较大的离散性。故在对截面承载率与裂缝宽度比关系的拟合过程中,去除了裂缝宽度比大于1.0的部分数据。图5c展示了拟合后的效果,拟合公式为线性,相似指数为0.887 86,具体公式如下:
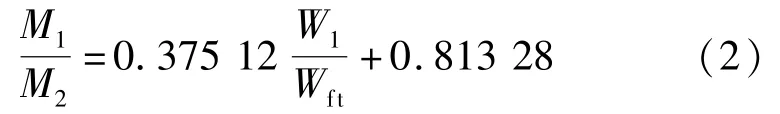
在日常桥梁维护中,W1可通过监测获取,而Wfk则可根据相关规范计算得出,根据式(2)可以计算出该状态下的桥梁承载率,然后可评估出桥梁的极限承载能力。
6 结论
本文依托大水沟大桥项目,基于相似准则进行了1∶4的模型试验。对截面挠度、混凝土应力应变数据进行了监测,并将实测值与理论计算值进行了对比,获得了合理的修正系数。最后,依据裂缝宽度对桥梁最大承载力进行了评估,根据裂缝宽度比与截面承载率之间的对应关系,进行了公式拟合。得出主要结论如下:
(1)混凝土桥梁的开裂荷载约为正常汽车荷载的1.2倍。跨中荷载小于300 kN时,荷载-挠度变化曲线呈直线,结构变形为弹性变形。荷载超过300 kN后,混凝土开始发生开裂,荷载-挠度曲线呈现出非线性关系。
(2)通过跨中挠度以及混凝土应力数据试验实测值与理论计算值的对比发现,在荷载等级较低时,实测值与理论值较为接近。若通过弹性方法对挠度进行分析,修正系数建议取1.6~2.0;若通过弹性方法对应力进行分析,修正系数建议取1.6~2.5。
(3)裂缝宽度比与截面承载率的拟合公式呈线性,相似指数为0.887 86,拟合效果较为优异。
