有限元仿真在《电机学》教学中的应用*

2022-09-30贾海媛罗振鹏

新教育时代电子杂志(教师版) 2022年19期

贾海媛王刚罗振鹏

（内蒙古工业大学电力学院内蒙古呼和浩特 010051）

电机是以磁场为媒介，实现机电能量转换或信号传输的装置，所以磁场作为电机中客观存在的物质，起到了极其重要的作用，而磁场又是一种看不到，摸不着的特殊物质，单纯通过理论讲解，会使得学生难以理解和接受，所以以交流电机的电动势学习为例，采用有限元仿真进行辅助教学，让学生更直观地理解电机内部磁场的作用，提高学生对电机学的学习兴趣[1-2]。

为了让学生更加直观地理解交流电机的电动势，本文通过建立永磁同步电机的模型，来分析交流绕组处于转子磁场作用下所产生的感应电动势。结合教学内容，分别对单根导体感应电动势、线圈感应电动势、线圈组感应电动势和相绕组感应电动势进行了仿真分析，从而引出短距绕组和分布绕组对感应电动势的影响，让学生更好地理解分布因数和短距因数的物理意义。

一、仿真模型的建立

以2极永磁同步发电机为例，建立其仿真模型，仿真模型由转子铁芯、永磁体、定子铁芯和线圈组成，为了忽略齿槽效应的影响，定子铁芯未开槽，定子线圈置于定子铁芯的内表面，为了使气隙磁场尽可能正弦化，永磁体采用了偏心设计，在气隙磁场的作用下，分别来仿真分析单根导体感应电动势、线圈感应电动势、线圈组感应电动势和相绕组感应电动势。单根导体感应电动势仿真模型如图1所示，其他情况的仿真模型根据需要仿真分析的感应电动势在定子内表面不同位置布置导体并进行串并联，电机的气隙磁场波形分别如图2所示。

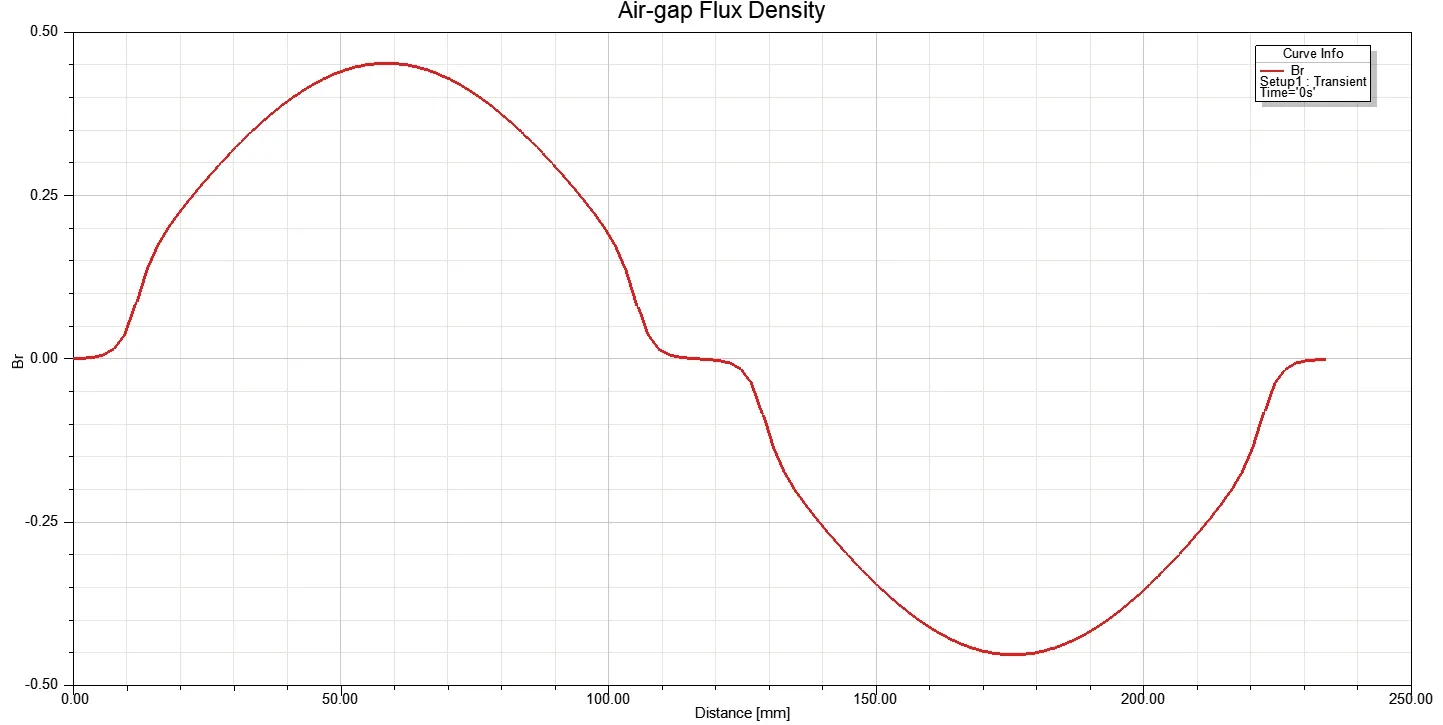
图2 气隙磁密波形

二、感应电动势分析

1.单根导体感应电动势

仿真模型如图1所示，将线圈匝数设置为1匝，电机转速设置为1500r/min，在气隙磁场的作用下仿真得到的就是单根导体的感应电动势，仿真波形如图3所示。

图1 仿真模型（单根导体）

由图3可知，单根导体感应电动势的波形与气隙磁密波形一致，当气隙磁密呈正弦分布时，单根导体感应电动势的波形也呈正弦分布。由于气隙磁密不是完全正弦化分布，所以可以对单根导体感应电动势进行傅里叶分解，得到其傅里叶分解结果如图4所示。

图3 单根导体感应电动势波形

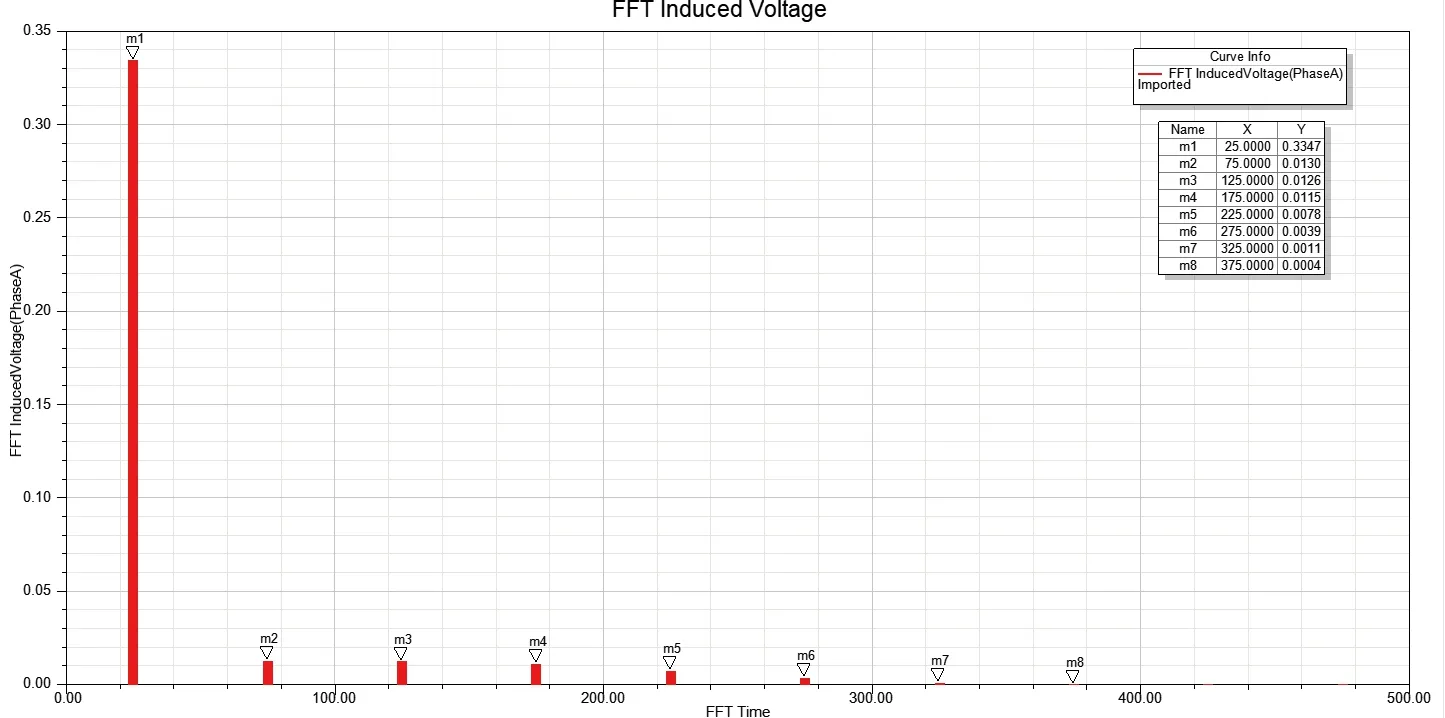
图4 单根导体感应电动势傅里叶分解

根据教学内容，首先来分析正弦作磁场作用下的感应电动势，所以先来分析感应电动势的基波分量。由图4可知，在已知气隙磁场的作用下，单根导体感应电动势的基波分量的有效值为0.2367V。

由推导得到的单根导体感应电动势计算公式E1= 2.22fΦ1可知，单根导体的感应电动势与频率及每极磁通量成正比，可以引导学生们采用有限元仿真，在改变电机转速、极对数、永磁体厚度等参数来分析其中某一个参数变化时对导体感应电动势的影响，从而加深学生们对公式的理解。

2.线圈感应电动势

（1）整距线圈

在单根导体感应电动势仿真模型的基础上，再增加一根导体，它与第一根导体相差180°，并与第一根导体组成一个整距线圈，其方向与第一个导体方向相反。仿真得到整距线圈感应电动势波形及其傅里叶分解结果分别如图5及图6所示。

图5 整距线圈感应电动势波形

图6 整距线圈感应电动势傅里叶分解

由仿真结果可知，整距线圈感应电动势基波分量的有效值为0.4733V，是单根导体感应电动势的2倍，结合单根导体感应电动势和整距线圈感应电动势计算公式也可以得到整距线圈感应电动势是单根导体感应电动势的2倍，即为两根导体感应电动势的代数和，仿真结果与理论推导完全吻合，通过仿真可以让学生直观地理解整距线圈感应电动势与导体感应电动势之间的关系。

（2）短距线圈

相比于整距线圈，同样可以利用有限元仿真来分析非整距线圈的感应电动势。以短距线圈为例，将第二根导体与第一根导体的距离减小至150°，此时两根导体便组成了一个短距线圈。仿真得到短距线圈感应电动势波形及其傅里叶分解结果分别如图7及图8所示。

图7 短距线圈感应电动势波形

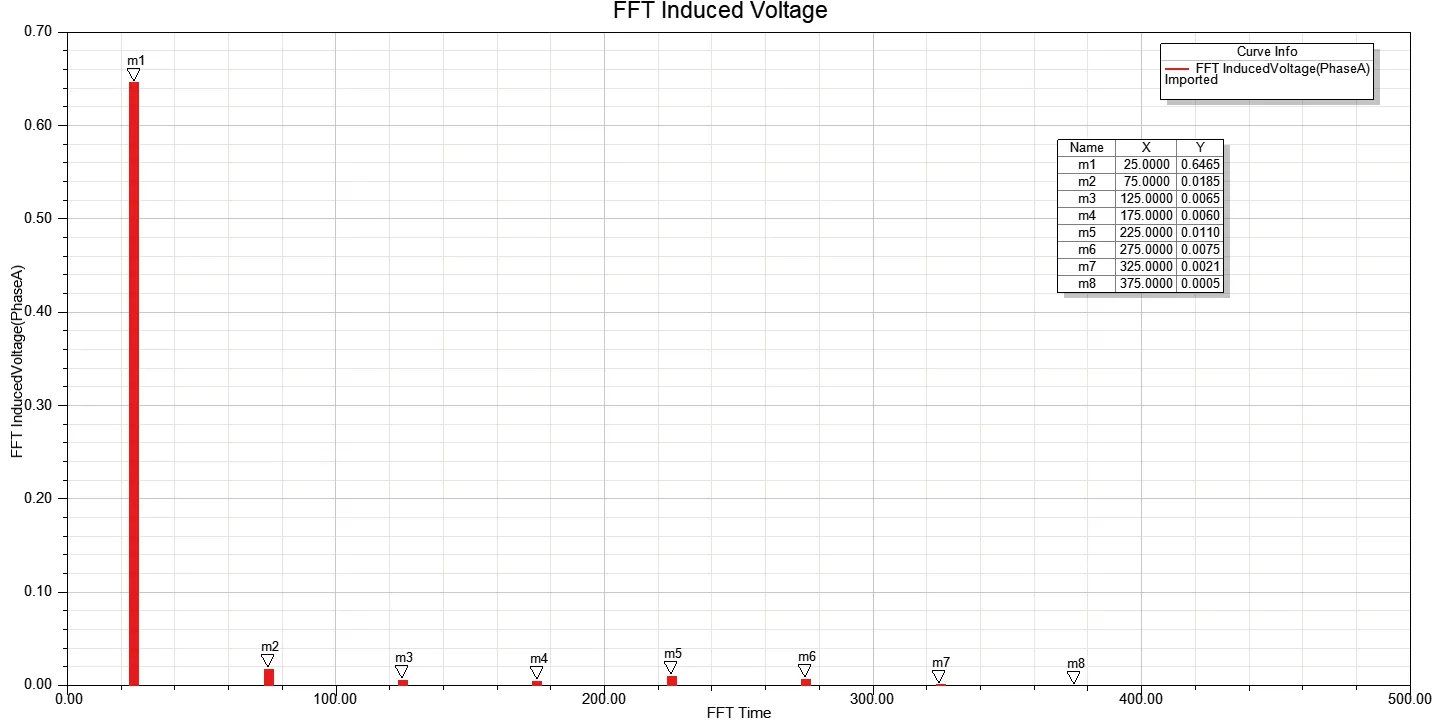
图8 短距线圈感应电动势傅里叶分解

由仿真结果可知，短距线圈感应电动势基波分量的有效值为0.4571V，整理得出整距线圈和短距线圈导体感应电动势的关系如表1所示。

表1 整距线圈与短距线圈感应电动势基波分量对比

由仿真结果可知，当线圈为短距线圈时，其感应电动势减小了，其减小比例可以用节距因数来描述，其物理意义是组成线圈的导体电动势相量和相比导体电动势代数和所打的折扣。

通过推导可以得到短距因数kp=，其中β为短距角，结合仿真参数可知，仿真中的短距角为30°，利用公式可以计算得到节距因数为0.9659，而仿真得到的结果也与计算结果完全吻合，所以通过仿真可以让学生直观地看到短距后其线圈感应电动势的变化以及节距因数对线圈感应电动势的影响。

上述仿真中导体的匝数均为1匝，而实际线圈一般采用多匝线圈，从而得到线圈感应电动势的计算公式为Ec=Nc Ec1= 4.44fNcΦ1。在短距线圈仿真模型基础上，将导体匝数设置为20匝，同样可以通过仿真得到多匝线圈感应电动势基波分量的有效值为9.143V，与公式计算结果吻合。

3.线圈组感应电动势

通过对交流绕组构成的学习可知相邻的各线圈依次串联构成线圈组，所以在仿真得出单个线圈感应电动势后，可以继续对线圈组感应电动势进行仿真分析。

假设电机每极每相槽数q=2，在线圈感应电动势仿真模型的基础上，再增加一个线圈，该线圈与第一个线圈相距30°，与第一个线圈串联构成线圈组。仿真得到线圈组感应电动势波形及其傅里叶分解结果分别如图9及图10所示。

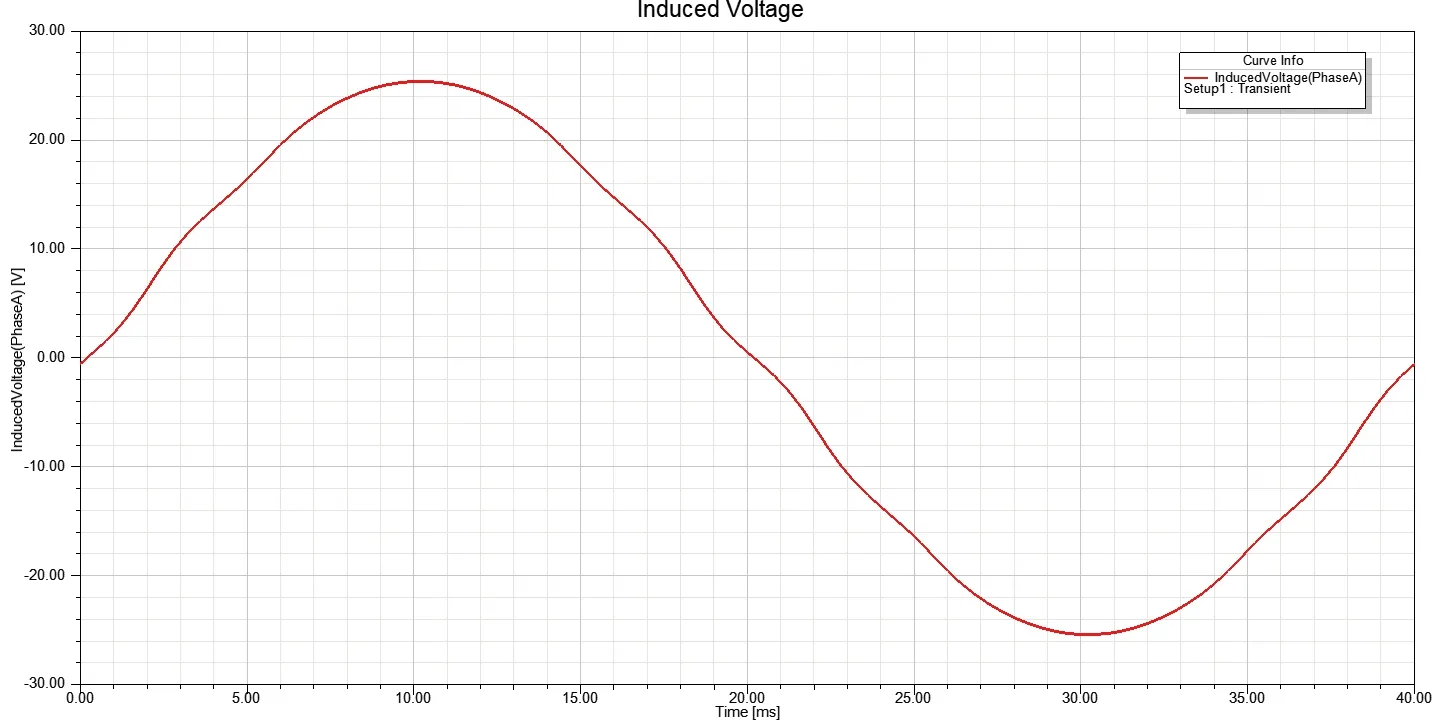
图9 线圈组感应电动势波形

图10 线圈组感应电动势傅里叶分解

由仿真结果可知，线圈组感应电动势基波分量的有效值为17.6637V，整理得出线圈和线圈组导体感应电动势的关系如表2所示。

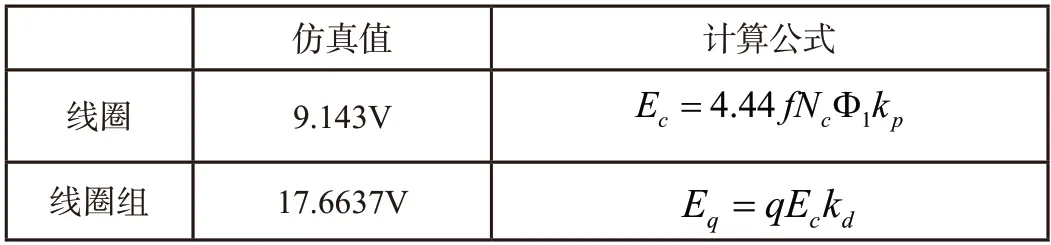
表2 线圈与线圈组感应电动势基波分量对比

由仿真结果可知，当q个线圈串联构成线圈组后，其感应电动势与q个线圈感应电动势代数和相比减小了，其减小比例可以用分布因数来描述，其物理意义是线圈电动势相量和相比线圈电动势代数和所打的折扣。

结合仿真参数可知，仿真中的槽距角α=30 °，每极每相槽数q=2，利用公式可以计算得到分布因数为0.9659，而仿真得到的结果也与计算结果完全吻合，所以通过仿真可以让学生直观地看到分布因数对线圈组感应电动势的影响。

4.相绕组感应电动势

线圈组通过串并联构成一相绕组，采用双层绕组时，线圈组数等于极数，在上述模型的基础上，建立相感应电动势仿真模型，仿真得到相感应电动势波形及其傅里叶分解结果分别如图11及图12所示。

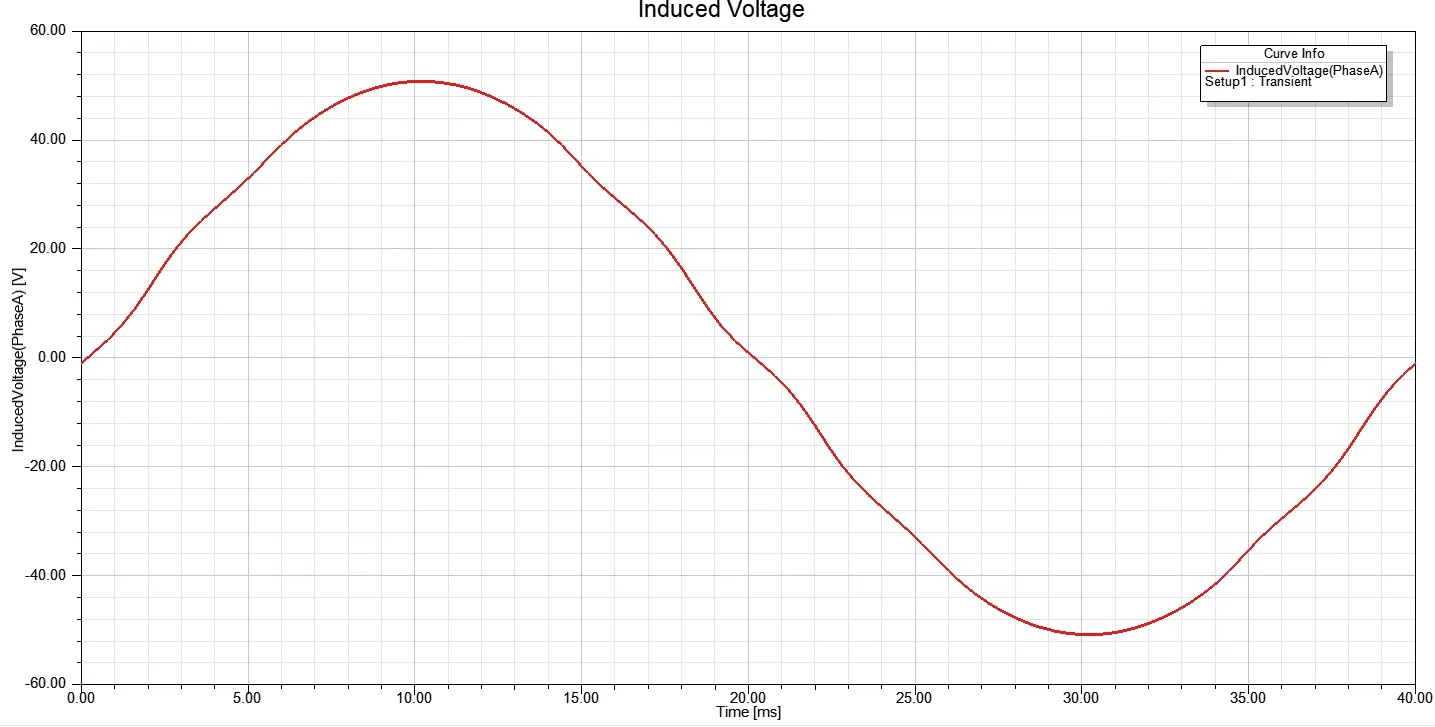
图11 相感应电动势波形

图12 相感应电动势傅里叶分解

由仿真结果可知，相感应电动势基波分量的有效值为35.3326V，结合仿真模型，相当于由2个线圈组串联得到相绕组感应电动势，即为上述线圈组感应电动势的2倍。

对于多极电机的仿真，可以引导学生自行建模，来对比分析线圈组间不同连接方式引起的感应电动势的变化，同时可以根据导体匝数设置的不同来对比相同匝数下单层绕组和双层绕组感应电动势的不同，从而更进一步加深对绕组构成的理解。

通过以上分析可知，对于交流绕组，当采用短距分布形式后，其总体作用使得感应电动势基波分量减小，那为什么在实际电机中仍采用短距绕组和分布绕组作为电机主要绕组形式，那么我们下面来进一步分析绕组短距和分布在其他方面的影响。

三、短距绕组和分布绕组的作用

在上面的分析中，仅关注了感应电动势的基波分量，我们也希望交流绕组的感应电动势为正弦波，而在实际电机中由于气隙磁场的非正弦使得交流绕组的感应电动势也不是正弦波。通过上述的仿真可以看到，感应电动势中不仅包含基波分量，同时也存在3、5、7、9等奇次谐波，且随着谐波次数的增高，谐波幅值减小。结合上述仿真结果，将整距线圈、短距线圈、线圈组的基波及各次谐波电动势整理如表3所示。

表3 整距线圈、短距线圈、线圈组基波、各次谐波感应电动势及其与基波比值

由仿真结果可知，当线圈为整距时，其基波分量相比短距时稍大一些，但各次谐波分量占比较大，当线圈短距后，其各次谐波均得以削弱，当线圈分布后，其各次谐波进一步被削弱。因此，交流绕组采用短距和分布的形式可以有效抑制感应电动势中的高次谐波。

采用短距绕组时，通过分析可知，当需要消除某次谐波时，只要选用比整距短的短距线圈便可，而电机中由于5、7次谐波幅值较大，所以常采用短即线圈节距为时可同时削弱5次和7次谐波，由仿真结果也可以看到5次和7次谐波电动势削弱幅度最大。

其削弱效果可以用谐波节距因数来描述，通过推导可以得到谐波短距因数

结合仿真参数可知，利用公式可以计算得到3、5、7、9次谐波节距因数分别为0.7071、0.2588、-0.2588和-0.7071，而仿真得到的结果也与计算结果完全吻合，所以通过仿真可以让学生直观地看到绕组短距对感应电动势中高次谐波的抑制作用。

采用分布绕组时，通过分析可知，其削弱效果可以用谐波分布因数来描述。

结合仿真参数可知，利用公式可以计算得到3、5、7、9次谐波分布因数分别为0.7071、0.2588、-0.2588和-0.7071，而仿真得到的结果也与计算结果完全吻合，所以通过仿真同样可以让学生直观地看到绕组分布对感应电动势中高次谐波的抑制作用。

通过分析和仿真可知，短距绕组和分布绕组对基波和谐波电动势的绕组因数的影响有很大的不同，采用短距和分布绕组后虽然基波电动势有所下降，但对削弱或消除谐波电动势的作用非常明显，因此在交流电机中广泛采用短距绕组和分布绕组[3-4]。

四、谐波磁动势削弱方法

1.采用短距绕组和分布绕组

由上分析可知，采用短距绕组和分布绕组可以有效削弱电动势中各次谐波。

2.采用星形连接方式

对于三相电机而言，绕组常采用星型连接，那么在线电动势中就不会出现3次和3的倍数次奇次谐波电动势，提取上诉仿真分析中的线感应电动势波形并进行傅里叶分解。通过仿真结果可以看到当绕组采用星型连接时，线电动势中的3次和3的倍数次谐波都没有出现，所以说采用星型连接是消除3次和3的倍数次谐波电动势的方法。

3.使气隙磁场正弦化

在实际电机设计中，常通过优化永磁体或磁极的形状来优化气隙磁场波形，使气隙磁场正弦化，这是削弱谐波电动势最根本的方法，上述仿真已经对永磁体形状进行了优化，后续可以引导学生重新建立仿真模型，同样采用表贴式的永磁同步发电机，分析对比当不对永磁体形状进行偏心设计以及不同极弧系数、不同偏心距时的相绕组感应电动势，从而更加直观地理解气隙磁场波形对感应电动势的影响。