数学文化融入高等数学“课程思政”：模式、切入点与措施*

司孟建 张建静

（河北机电职业技术学院 河北邢台 054000）

作为理工类院校大学生必修的一门重要通识课，高等数学在“课程思政”中发挥着关键的育人作用。从“课程思政”育人角度看，目前的研究集中在数学文化课程如何思政育人、基于数学文化视角的高等数学“课程思政”两方面，且后者多以数学史、数学精神等为切入点。鉴于数学文化包含数学的思想、精神、方法等及其形成和发展，又包括数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系等，[1]文章从“课程思政”的视角，全面挖掘数学文化的内涵及育人价值，提出了数学文化融入高等数学“课程思政”的育人模式、切入点与措施。

一、数学文化融入高等数学“课程思政”的育人模式

（一）育人目标

数学的文化价值主要指数学对人类观念、精神和思维方式的养成所具有的重要影响。[2]具体而言，数学文化具有德育、美育、思维训练的教育价值，[3]这和“课程思政”的价值理念相契合。依据对教育价值的分析，可确立包含改善数学知识认知、加深思想方法领悟、激发数学学习情感、培养数学理性精神[4]、树立正确的数学观、加强适当逻辑思维训练及形成一定数学应用能力[5]等在内的数学文化视角下高等数学“课程思政”综合育人目标。

（二）育人模式

在育人目标指引下，构建以高等数学知识为载体、以数学文化资源为媒介、以实现数学文化育人价值为落脚点，渗透“课程思政”的育人模式（见图1）。即高等数学课程、数学文化、“课程思政”之间相互联系、相互促进，共同构建了从知识学习到文化形成，再到思想引领三位一体的高等数学“课程思政”体系。[6]其中高等数学课程是数学文化和“课程思政”的有效载体，高等数学学习有助于提升数学文化、渗透“课程思政”；数学文化的融入将高等数学课程提升到了数学文化教育层面；“课程思政”有助于引领学生从更宽、更高的视野去学习高等数学课程和感受数学文化，提升高等数学的综合育人价值。

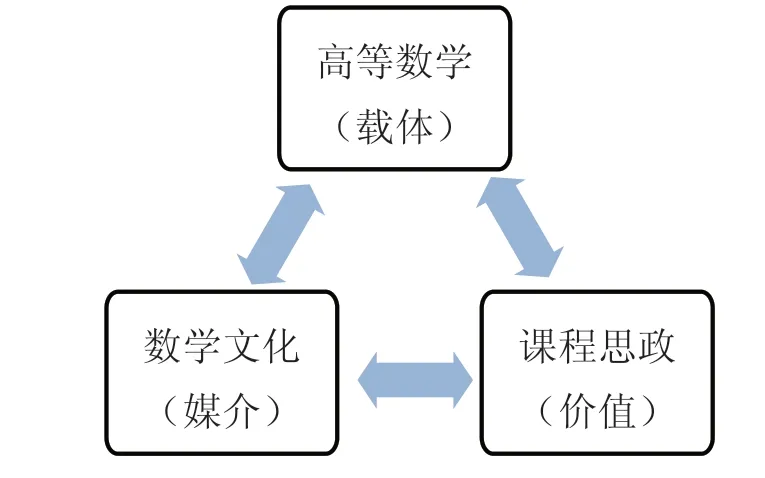
图1

二、数学文化融入高等数学“课程思政”的切入点

以高等数学知识为载体，从历史与现实、纵向与横向多个角度挖掘数学文化融入高等数学“课程思政”的切入点，以发挥其在“课程思政”育人中的媒介作用。

（一）历史挖掘与现实应用

1.挖掘知识背后的历史

挖掘数学知识背后的历史主要包括客观知识的来源与真实的数学家故事两个方面：（1）数学知识来源于客观历史，很多概念诞生于不同背景下的现实案例，其客观性使人信服，其实践性利于学生类比迁移，其曲折性可启迪人生。如通过变速直线运动的瞬时速度、曲线的切线斜率等实例引入导数概念，不仅让学生认识到数学因应用性而源于现实生活，又因抽象性而高于生活，而且有利于训练学生特殊与一般的数学思维，即由特殊具体案例归纳至一般抽象模型，以凸显事物本质，再迁移至更多涉及变化率的问题，从而拓展学生对数学的认知视野与应用范围。而对于分母无穷小的曲折探索展现了一定的历史发展规律，可启迪人生。（2）数学家的故事重在通过对数学家真实事迹的透视与剖析，展现一代代数学家奋斗的初心与爱国情怀、钻研的精神与科学奉献等品质，为学生树立精神上的榜样及对科学的崇尚与敬畏。

2.从知识的实际应用入手

数学源于实际，又应用于实际，根据不同角度可划分为历史或现实应用、学科内部或跨学科领域应用。考虑到高职学生以“应用”为目标，宜采用案例教学法，可从两方面着手：（1）学科内的古今应用。生活生产实践的需要是推动数学持续向前发展的不竭动力。历史上一些实际问题或具体案例因接近实际，降低了学习新知的门槛，成了为今天课堂上学习新知的引例。教师可借此机会以用促学、以例明理。如曲边梯形面积引入定积分、变速直线运动瞬时速度引入导数概念等。（2）跨学科的现实应用。数学在现实生产生活及当代高科技领域均具有广泛应用。其教育意义为：①将数学聚焦实用化有助于扭转学生对数学无用论的传统观念，端正学习态度。如利用数学期望验证核酸检测中“10 合1”混采检测技术的合理性。②数学的多领域应用利于学生见证知识的力量。如利用贝叶斯公式量化核酸检测呈阳性的患病概率。③通过对数学在我国高科技领域的实际应用增强学生的民族自豪感。如利用无穷限反常积分计算我国北斗卫星覆盖面问题。

（二）横向迁移与纵向升华

1.从知识体系本身入手

高度的抽象性使高等数学本身就蕴含着丰富的哲学原理或辩证思维。为此，针对高等数学知识体系，可从两方面着手：（1）探寻知识创立之想。因许多数学理论的创立源于一代代数学家对现实生活中遇到的数学问题的思考，在该思考之初或过程中所产生的想法就是创立之想。其经过不断的完善变成了各种数学思想或思考问题的角度等，触及知识本质，却意境宏大、通俗易懂。如贝叶斯公式的创立就源于人类最朴素的想法：当新信息不断出现，也就可以不断更新原先的认知，其充满辩证思维，道理深刻。（2）提炼知识本义之道。对知识本身所折射出的哲学原理或辩证思维等要素加以提炼，形成育人元素。即教师可通过对知识本身的哲学分析，挖掘其蕴含的育人元素。如函数极限定义本身展现了有限与无限、量变与质变、静止与运动等辩证关系。

2.对知识进行延伸与拓展

基于“课程思政”综合育人的现实需要，教师可以在知识本身含有的直观育人因素基础上，通过赋予人之情感将育人目标提升至一个更高、更宏大层面，以实现知识联系生活，迁移育人。具体做法为：（1）内在关系挖掘角度。如对于微积分基本公式来讲，在学科内，它沟通了微分学与积分学的联系，展现的是微积分内容的统一美。在学科外，教师可以进一步提升至社会生活中很多现象都具有统一的发展趋势，如全球经济一体化等现象，从而自然衍生出要构建人类命运共同体的理念。（2）直观图形观察角度。即教师通过引导学生对图形或数学公式的直观观察而联想出育人元素。如通过观察函数曲线的极值情况，引导学生正确看待生活中的挫折与人生起伏。

三、数学文化融入高等数学“课程思政”的具体措施

在以上融入模式指引下，可结合数学文化或数学学科的主要特征，选择典型的数学文化成分与高等数学“课程思政”相融合。

（一）基于数学文化的特征

1.通俗性：科普数学发展史

考虑到高职学生基础薄弱、学习兴趣低等特点，教师可精选数学史并将其穿插于教学中，以展现相应知识点的来龙去脉，从而引导学生形成对科学进步曲折历程的客观认知，促使学生迁移至对现实人生的思考。如微积分曲折的发展历史可启发学生树立理性的人生态度，因此数学发展史的融入不仅有助于促进学生对知识的理解，而且可以培养学生对真理的理性认知、正确认识数学地位及其文化价值，从而树立辩证唯物的三观。

2.趣味性：借用历史名题案例

高等数学本身具有高度抽象与逻辑严谨等特征，基于HPM 教育思想[7]，教师在实际教学中可适当弱化理论推导，有选择性地引入数学文化中的一些有趣且易于理解的历史名题或案例。这不仅有助于拉近理论知识与实际生活的距离，降低学习的认知门槛，而且赋予学习资料以历史感，增强了学生的学习兴趣，从而由易到难，循序渐进，有效达成学习目标，如借助复利模型引入第二重要极限。

3.文化性：呈现数学与社会的联系

高等数学与哲学、文学、生活等具体领域联系密切，其价值也体现于它与各领域的相互联系之中。为此，在教学中教师可通过引入高等数学与相关具体领域相结合的案例或现象，以呈现数学与其他知识领域之间关联的方式，多维度丰富教学内容。这不仅有利于学生更深刻地认识高等数学的作用与地位，而且有助于全面提升高等数学的综合育人价值。此外，对高等数学在我国高科技技术领域的现实应用的介绍还可以有力地提升学生的民族自豪感。

4.教育性：拓展数学教育价值

数学文化的教育性指数学教育对人类的成长所具有的特殊意义，即数学对人类理性精神的养成与发展、思维训练以及创造性才能的发展具有重要作用。郑毓信先生也曾强调数学教育对发展人类“数学理性”的重要意义，并提倡科学精神与人文精神的有效融合。[8]因此高等数学应特别关注数学的文化价值，这不仅能提升大学生的数学文化素质与创新精神，而且对学生的成长成才具有重要的促进作用。

（二）基于数学学科的特征

1.应用性：强化数学建模的能力

高度的抽象性决定了数学应用的广泛性，而数学建模架起了数学知识与实际问题之间的桥梁。为此，教师可以选择贴近于学生熟悉的自然科学或社会科学中的实际应用案例，利用数学建模思想与流程，让学生从实际背景中分析、提炼并解决相应数学问题。依托于数学建模的案例教学等方法不仅有利于提升学生用数学建模解决实际问题的意识与能力，而且可以让其领略数学的神奇力量以及树立学习有用论。

2.逻辑性：训练数学思维方式

数学语言是数学思维的外在表现形式，是训练学生数学思维的有利工具。在教学中，教师可以引导学生在实际问题解决的全过程中练习使用数学语言来表达各环节，即用数学的思维方式和方法去观察、思考、理解和解决问题。这不仅有利于培养学生严谨而科学地思考、分析及解决问题的能力，而且有助于其认识到数学演绎推理下结论的精确性以及数学思维对科技进步的特殊贡献。

3.抽象性：分析数学的哲学内涵

高度的抽象性决定了数学对事物间内在规律与本质揭示的深刻性，使得其从概念、运算、思想方法乃至解决问题的过程等都蕴含着丰富的哲学原理或辩证思维。为此，教师应不断提升自身的哲学理论高度，尤其是对与数学相关联的哲学理论的深刻领悟，扩大自身格局与视野；其次，在教学中要善于挖掘教学内容蕴含的哲学内涵与辩证思维，并通过巧妙的设计穿插于教学，以理育人。对知识背后哲理言简意赅的揭示有利于学生对事物本质与普遍规律的认识与把握，从而树立科学的世界观。

4.艺术性：展现数学数形之美

数学的广泛应用性使其与音乐、绘画、分形等联系密切。随着计算机的飞速发展，这种联系更是以直观可感的形式表现出来。如借助计算机绘图软件所画各种复杂、高维图形让人惊叹数学的神奇力量。此外，数学公式等所展现的各种变量间的对称、和谐、统一等特征也深刻反映了数学中的美学特性。这不仅有利于学生从数与形的角度领略数学美的特征并提升自身审美水平，而且彰显了数学对事物间关系的深刻揭示以及对生活的超越性。

5.科学性：弘扬数学理性精神

前提的确定性与推理的逻辑性保证了数学结论的客观真理性。在高度发展的现代社会，我们所遇到的事情越发复杂，能否保持一种理性的态度，能否用数学思维去分析和解决问题显得越发重要与迫切。如对买彩票中大奖、抽签顺序与公平性等现象的认识就要求学生具备科学理性的态度，不可仅凭直觉下结论。数学以其客观性与科学性使其具备了高度的理性，而这种理性对学生的理性态度、理性精神以及批判性思维的培养与塑造不可或缺。

6.人文性：解读数学家事迹

数学家的事迹及其背后的精神与思想境界是数学文化的重要组成部分。如数学家的敬业精神不仅表现在其对数学几十年如一日的坚持与专注，而且体现在其对祖国发展需要的深切关怀。像我国伟大数学家华罗庚，不仅数学造诣极高，而且他为广泛推广优选法而四处奔走的行为体现的是一代伟大科学家的崇高科学精神与深厚爱国情怀。因此，教师在教学中适当穿插古今中外数学家学习、研究数学的事迹，不仅能够增添课堂的故事性，而且有助于培养学生实事求是、坚忍不拔的科学态度和敬业精神等品质。

结语

数学文化资源丰富且具有多维度的育人价值，基于此认识，本文从数学文化融入高等数学“课程思政”的模式、切入点以及具体措施三方面进行了探讨，旨在通过数学文化融入高等数学“课程思政”提升学生的综合数学素养，尤其是引导学生形成正确的数学观。