求解多约束矩阵最小二乘问题的数值方法❋
2022-09-30吕照美刘新国
吕照美,刘新国
(中国海洋大学数学科学学院,山东 青岛 266100)
1 研究内容
本文研究三约束矩阵最小二乘问题

(1)
X∈εpsd∩P∩B
其中
εpsd={X∈Rn×n;XT=X且λmin(X)≥ε},
B={X∈Rn×n;L≤X≤U},

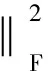
〈A,B〉表示A与B的内积,(A,B)= tr(ATB),tr(A)表示A的迹。记号A≤B表示Aij≤Bij,其中1≤i≤m,1≤j≤n。
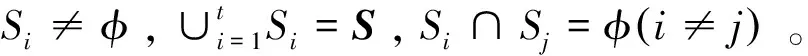
对应的,
L=L1+L2+…+Lt,
U=U1+U2+…+Ut,
(2)
L,U有上述分裂,其中Li和Ui分别是L和U在Si上的投影,并记
(3)
上述问题出现于统计和数量经济学等领域。统计学中的一个经典例子为:求一个到样本协方差矩阵最近的对称正定并且有一定结构的矩阵。这种有特殊结构的协方差矩阵[1]经常出现在物理、生物、心理学和社会科学模型。经济学中的一个例子[2]是获得效用函数问题,在这种情形下,拟合矩阵必须有界且对称,同时它的最小特征值必须大于某一特定的正数。

由于Dykstra交替投影算法本身收敛较慢且内迭代中SPG方法非单调,使得整个算法收敛更慢。且文献[12]中设置内外迭代次数上限均为5 000次,数值实验表明,SPG达到迭代次数上限时存在没有收敛或没有达到精度要求的情况。文献[12]中要求A,BT列满秩并假定可行集非空以保证解的存在性与唯一性,但并未给出判断可行集是否为空的方法以及在可行集上得到的点是否为最优解的条件。
在本文中,我们把Majorize-Minimize(以下简称MM)方法与Dykstra算法结合,提出求解式(1)的一种交替投影迭代方法。MM方法是一种单调收敛方法,Han[13]利用对偶性推导了Dykstra方法,并分析了其收敛性。
2 理论结果
2.1 问题的等价形式
令BP=B∩P,则
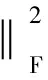
(4)
其中
(5)
这里,li和ui如式(3)定义,显然式(4)等价于式(1)。
2.2 可解性
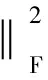
[tf(X)+(1-t)f(Y)]-f(tX+(1-t)Y)=
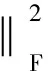
(6)
定理1令Ω=εpsd∩BP,设Ω≠φ,那么
(1)f(X)在Ω上有最小点。

证明 显然,B为有界闭凸集,P为凸集,而由
λmin(tX+(1-t)Y)≤tλmin(X)+(1-t)λmin(Y),
t∈[0,1],XT=X,YT=Y,εpsd为闭凸集,如果Ω≠φ,则Ω为有界闭凸集,而f(X)为连续可微函数,因此f(X)在Ω上有最小点。

证明毕。
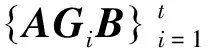
推论1如果Ω≠φ,而A和BT列满秩,那么式(1)的解存在且唯一[12]。
下面分析Ω≠φ的条件。
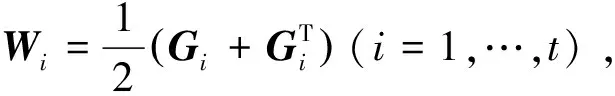
记δi=λmin(Wi),υi=λmax(Wi)则
{yTWiy:y∈Rn,‖y‖2=1}=[δi,υi]。
从而,如果
则
定理2如果
(7)
那么Ω≠φ。
2.3 最优性条件
定理3X*∈Ω为最小点的充要条件为
tr{(X-Y)TAT(AX,B-C)BT}≥0,∀X∈Ω。
(8)
证明 如果X*为最小值点,则对∀t∈[0,1]有
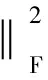
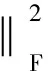
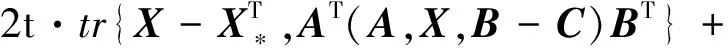
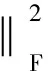
从而(8)式成立,否则取充分小,则得矛盾。
假设(8)式成立,则∀X∈Ω,



证明毕。
注2式(8)不易验证,下面给出一个充分条件。
推论2如果X*∈Ω,且
tr{(X-X*)AT(AX*B-C)BT}≥0,∀X∈Bp,
(9)
则X*是原问题的最小点。
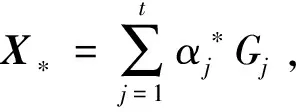
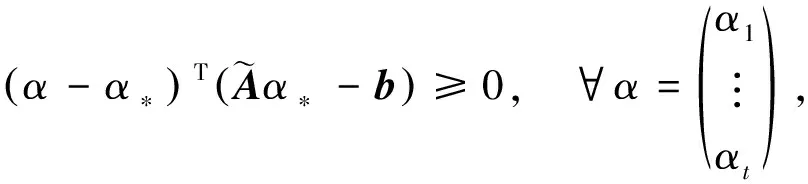
li≤αi≤ui(i=1,…,t)。
(10)
其中
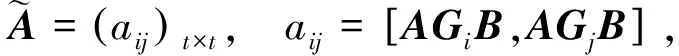
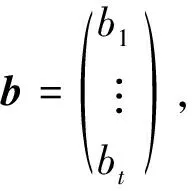
bi=〈AGiB,C〉。
又
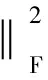

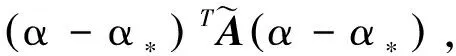
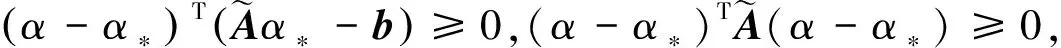
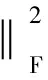
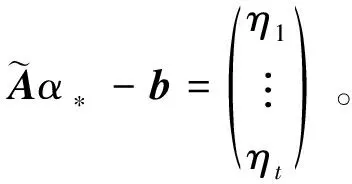
一方面,如果式(10)成立,则
(11)
另一方面,如果式(11)成立,则
有式(10)成立。
因此,推论2的等价形式为
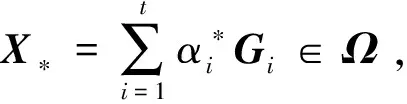
(12)
则X*为原问题的最优解。
3 算法
MM算法是求解最优化问题的重要方法。为了求解问题(1),设当前迭代点为X(k),那么
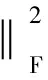
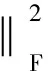
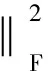
2tr{BT(X-X(k))TAT(AX(k)B-C)}+
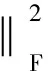
(13)
显然,gk(X(k))=f(X(k)),因此有MM算法:
(14)
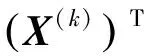
tr{BT(X-X(k))TAT(AX(k)B-C)}=
tr{(X-X(k))TAT(AX(k)B-C)BT}
且
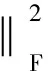
2tr {(X-X(k))TAT(AX(k)B-C)BT} =
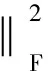
其中Ck与X无关,而
(15)
由此可知式(14)等价于
(16)
因此提出算法MM-Dykstra Method如下。

步骤2:计算
步骤3:计算
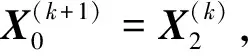
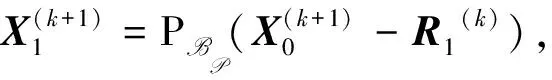
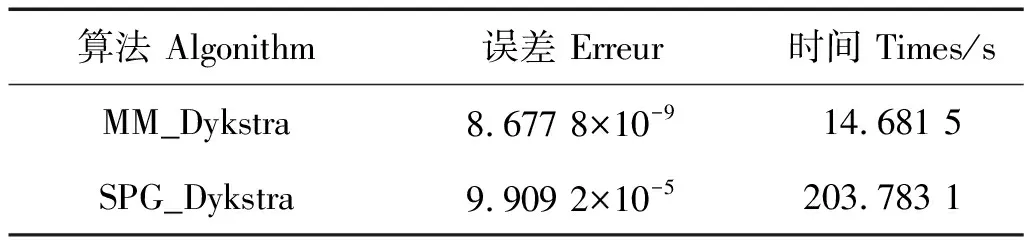
计算ck+1=‖X(k+1)-X(k)‖,如果ck+1 Boyle和Dykstra证明了Dykstra算法的收敛性[14]。 由式(14),gk(X(k+1))≤gk(X(k))≡f(X(k)),且gk(X(k+1))≥f(X(k+1)),所以{f(X(k))}单调递减。因此,在每次迭代仅需要求解两个子问题。 其一是 (17) 其中Q是一个正交矩阵, Λ(1)=diag(μ1,…,μs), Λ(2)=diag(μs+1,..,μn), μ1≥…≥μn≥ε>μs+1≥…≥μn, 则式(17)的解为 (18) 因此, Pεpsd(X)=QΛ(i)QT。 (19) 另一个是 (20) Z=Z1+…+Zt, (21) Zi与Gi有相同的结构,从而有 (22) (23) 其解为 (24) 则 注3有多种取法。 由 其中, aij=〈AGiB,AGjB〉, 由于MM算法是一种投影梯度法,一般而言收敛较慢。Lopez和Raydan[16]指出,Dykstra算法有时收敛也很慢,可以使用文献[10]中的加速技巧,这里我们考虑选取特殊的来实现对算法的加速。 因此可以如下构造初始迭代点 (2)取 (Gi是Hadamard积),ϑi满足li≤ϑi≤ui且 |ϑi|=min{|αi|:li≤αi≤ui}。 在例1和例2中,L为零矩阵,U为所有元素均为3的矩阵,TOLin=1×10-7,TOLout=1×10-8,MM算法的最大迭代次数为5 000,P≡Rn×n,且在本文中 即在两种算法比较的过程中所用的停止准则一致。 例1 对于文献[12]中的实验例子:ε=0, B=I, 利用文献[11]中算法4.1得到的结果与本文算法的结果对比见表1。 表1 MM_Dykstra算法与SPG_Dykstra算法的时间、误差、残差比较 其中在两种算法中X*表达相同,均为 例2 取C=50×rand(m,p),ε=0.1,此处以10阶为例,计算结果见表2。 表2 MM_Dykstra算法与SPG_Dykstra算法10阶矩阵的误差与时间比较 从例1和例2两个例子的对比中,我们能够看到MM_Dykstra算法无论是在残差还是在时间上都有了一定改善。 本文提出了MM_Dykstra算法来求解多约束矩阵方程最小二乘问题,该方法将三约束问题转换为双约束问题,有效地减少了交替迭代次数。数值实验结果表明,与SPG_Dykstra方法相比,本文算法具有更快的求解效果,结果精度也相对更高。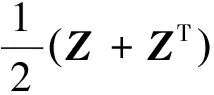
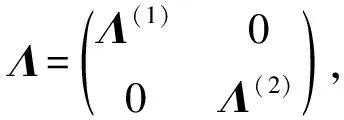
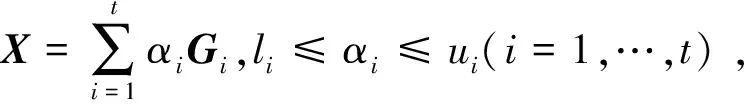
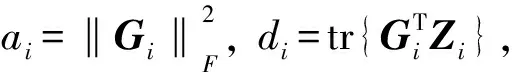

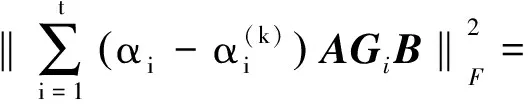
4 初始点

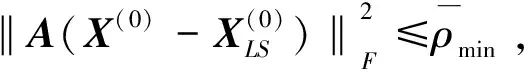
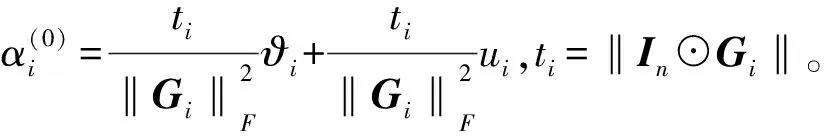
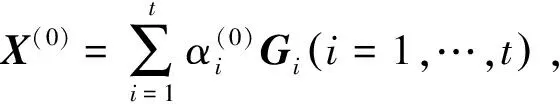
5 数值实验

6 结语
