球状结构物在波动液化土中沉降过程研究❋

吴汉儒，许兴北，任宇鹏，许国辉❋❋

(1.中国海洋大学海洋环境与生态教育部重点实验室，山东 青岛 266100；2.中国海洋大学山东省海洋环境地质工程重点实验室，山东 青岛 266100)

在极端波浪条件下，底床内的孔隙水压力发生积累，达到上覆土体的有效应力时，底床土体会产生液化现象，导致近岸建筑设施由于地基承载力的丧失而发生倒塌倾覆，造成不可估量的人员伤亡和财产损失[1-3]。研究液化土中块体结构物沉降的规律，对评估海洋构筑物的稳定性具有重要意义。

一般认为，当海洋土体中的超孔隙水压力达到或超过上覆土体的有效应力时，液化发生[4-6]，坐落于底床上或埋置于底床中的构筑物，如锚、桩基、管线等，会因此发生下沉或上浮。波致液化土体做与上覆水体类似的波动[7]，结构物在液化土体中，受到液化土的裹挟，在下沉或上浮的同时，也可能出现与液化土类似的周期性运动[8]。轻质结构物在上浮的同时会做与液化土类似的椭圆轨迹运动，并最终在水-液化土界面处做上下振动；重质结构物会逐渐下沉，下沉的极限深度随比重的增大而增大，但存在一个极限值，同种材质的结构物中，块体较管道的下沉深度大[9]。Groot等将波浪作用下海床地基失稳分为液化破坏、逐步液化破坏、逐步破坏和摆动破坏，提出液化流动破坏仅发生在相对密度低、排水能力差的情况下[10]。对桩基础周围波浪液化数值模拟结果表明，桩基的存在会造成土体初始有效应力减小以及超孔隙水压力差值的减小，随着桩插入深度的增加，初始有效应力对海床液化的影响逐渐超过超孔隙水压力[11-12]。

将液化后的土体视为流体进行研究已有一定的历史。1994年，Kawakami等用拖球法和粘度计法对液化土的流体性质进行了研究，发现液化土的粘滞性由相对密实度控制[13]。随着试验手段的发展，不同学者采用拖球法[14]、拖管法[15]、落球法[16]、振动扭剪三轴仪[17-18]以及离心机[19-20]等不同手段研究液化土的流体力学性质。陈育民等采用扭剪试验探究了液化土剪应力与剪切速率的关系，提出液化土是一种剪切稀化非牛顿流体，且相对密实度、围压等参数都会对其粘滞性产生影响[17]。虽然前有学者对不同性状土体的液化特性和结构物浮沉现象开展了研究，但对于结构物沉降的过程及过程表达尚未明确给出。本文主要考虑球状结构物在波动液化土中的沉降问题，首先推导液化土中球体的位移公式，并采用铁质密度球模拟结构物，开展波浪水槽试验，获取密度球在液化土中的波动沉降过程，给出结构物沉降的过程表达，为波动液化土中结构物的浮沉描述提供数学表达方法。

1 球体在波动液化土中运动轨迹

球体在波动液化土中的运动是由两种运动复合而成：其一为球体受到液化土的裹挟所做的与液化土质点相同的椭圆轨迹运动；其二为球体因自身密度与液化土密度的差异，在自身重力作用下所做的相对液化土的垂直沉降运动(见图1)。

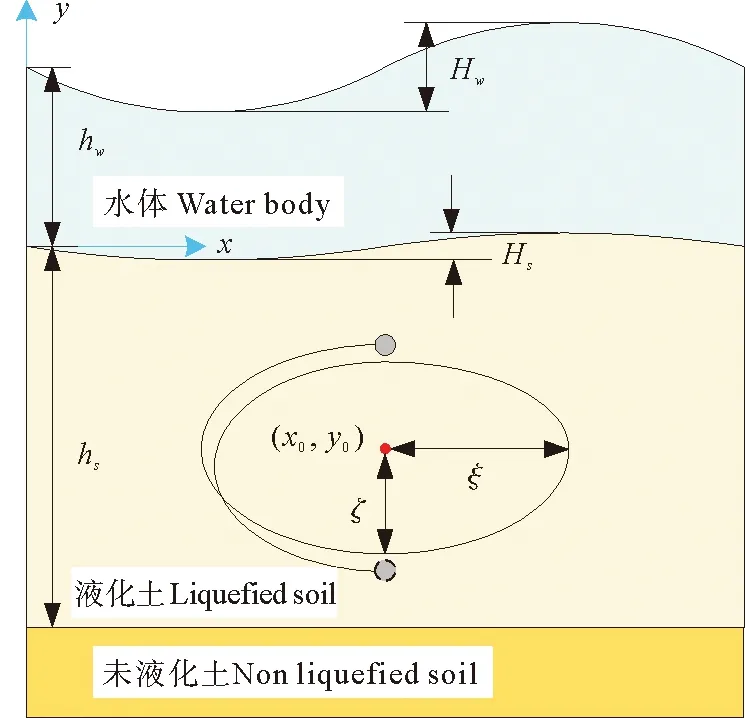
(Hw：海面波高；hw：水深；Hs：水-液化土界面波高；hs：液化深度；(x0,y0)：球体振动的平衡位置。Hw: wave height at sea level; hw: water depth; Hs: wave height of water-liquefied soil interface; hs: liquefied depth;(x0, y0): the balance position of vibrating sphere.)

1.1 球体在波动液化土中的椭圆运动轨迹

当海面的波动为小振幅波时，水质点围绕平衡位置做小振幅的周期运动，其运动轨迹为一封闭椭圆，椭圆的长、短轴长度由海面波高Hw、波数k以及平衡位置所处水深y0决定。

以往的波浪水槽试验结果表明，波致液化土-水体界面做与水面相似的波动，二者波长和周期相同[21]；波致液化土颗粒随水质点一同做椭圆轨迹运动，随着深度增加，运动轨迹的长短轴直径衰减[22]。球状结构物受液化土裹挟，做与液化土颗粒相同规律的运动。因此，在可知水-液化土界面波高情况下，可以在界面处建立坐标系，仿照小振幅波水质点位移公式的形式，写出不考虑球体自身沉降的条件下，相对平衡位置(x0,y0)的水平向位移ξ、竖直向位移ζ的表达式：

(1)

(2)

式中：Hs为水-液化土界面的波高；k为波数；hs为液化深度；ω为角频率；t为时间。

1.2 球体相对于液化土的沉降速率

液化土中的块体结构物，由于密度和周围的液化土有差异，在受液化土裹挟做椭圆运动的同时，会在自身重力作用下发生沉降。在一定的液化深度内，液化土性质均匀，粘滞系数不变，球体所受的重力、浮力和液化土竖直向阻力平衡[23]，球体竖直向平衡位置y0以速度v匀速降低：

y0=-vt。

(3)

实际上，球体无论是先在上覆水体中沉降后进入液化土，还是预先置于土床表面再沉入液化土，都应在沉降的初期经历一个变速阶段。但研究表明，该阶段的持续时间一般非常短，不足0.1 s[24]，故本研究舍弃此变速段，认为式(3)成立。陈昌昀等[23]证明了在球体的匀速沉降阶段，液化土阻力Fv可以使用静水沉降的斯托克斯公式来计算：

Fv=(ρs-ρl)Vg=6πηrv。

(4)

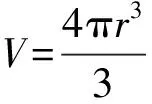
(5)

以往的试验表明球体水平向的平衡位置一般不发生明显变化，即x0维持不变。

1.3 球体在波动液化土中运动轨迹的表达

根据以上描述，球体在液化土中的运动，应为沉降运动和椭圆周运动的复合运动。将球体在x0=0的位置释放，那么球体的位置坐标(x,y)=(ξ,y0+ζ)。将(3)代入(1)和(2)，得

(6)

(7)

于是，只要通过实验测量出波长、周期、界面波高等数据，就可以绘制对应条件下球体的水平、竖直向位移-时间曲线，以及球体的运动轨迹。

采用与上述相同的方法，可以推导出海面波动为二阶斯托克斯波情况下球体的位移表达式：

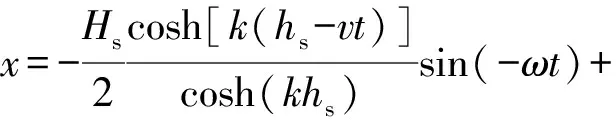
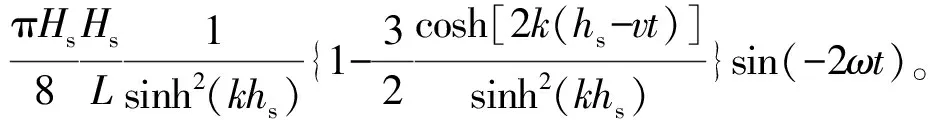
(8)

(9)

2 球体在波动液化土中运动轨迹测量试验

为检验球体在液化土中波动沉降过程表达的准确性，本文设计了球体在液化土中沉降的波浪水槽试验。

2.1 测量原理与装置

波浪水槽试验可以呈现结构物在液化土体中的沉降现象[25]，然而不能获得结构物沉降的实时过程。采用落球测量液化土粘滞系数的方法[7,23]，利用单个的激光位移计仅能够获得球体沉降的垂向位移，无法同时获得球体在波动液化土中的水平位移和垂直位移。本文改进了落球法的位移测量方案，采用球体位置三角形控制双激光位移计测量方案，可以清晰获得球体在波动液化土中的运动轨迹。

球体位置三角形控制双激光位移计测量原理：如图2所示的坐标系中，如三角形ABC的三边长a、b、c已知，那么点C的坐标(x,y)可通过解三角形获得：

(10)

(11)

落球法试验中，设计2个激光位移传感器，进行三角形边长a和b值的实时测量。而三角形边长c为可知的常数值。由于三角形ABC的三边长a、b、c均实时可知，则处于三角形C点的球体在液化土中的水平和垂直位移可以实时计算给出。

具体测量装置由支架、滑轮、激光位移传感器、密度球、尼龙线、激光反射板等组成，装置示意图和照片见图2。

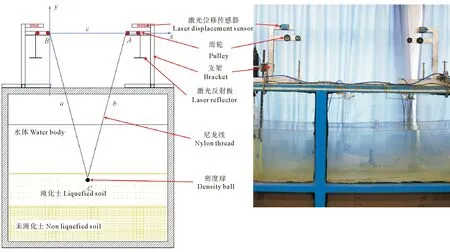
图2 落球试验装置示意图和照片

两个支架尺寸完全相同，结构左右对称。每侧支架上安装两个滑轮，防止激光反射板的摆荡。位移传感器是德国生产的DT-35型激光位移传感器。两支架间距81 cm，固定于水槽上方，两支架之间的中点位于试验底床中部。试验所用的密度球为直径3 cm的光滑铁球，质量为109.7 g。密度球上用胶连接两根长160 cm，直径0.1 mm的尼龙线，线端部悬挂激光反射板。激光反射板上附有配重盒，用以将线拉直，同时调节密度球的等效质量。

2.2 底床设置与试验过程

试验用土体是取自黄河三角洲的粉质土，其粒径级配曲线见图3。将试验所用的粉质土和水混合搅拌成均匀泥浆，控制其含水率在33%左右。随后将混合好的泥浆移入水槽铺设成尺寸为2.6 m×0.5 m×0.6 m的底床。水槽总长14 m。向水槽内加水至床面上40 cm处，静置固结7日，7日后用直剪试验测得其内聚力c=6.5 kPa，内摩擦角φ=32°。

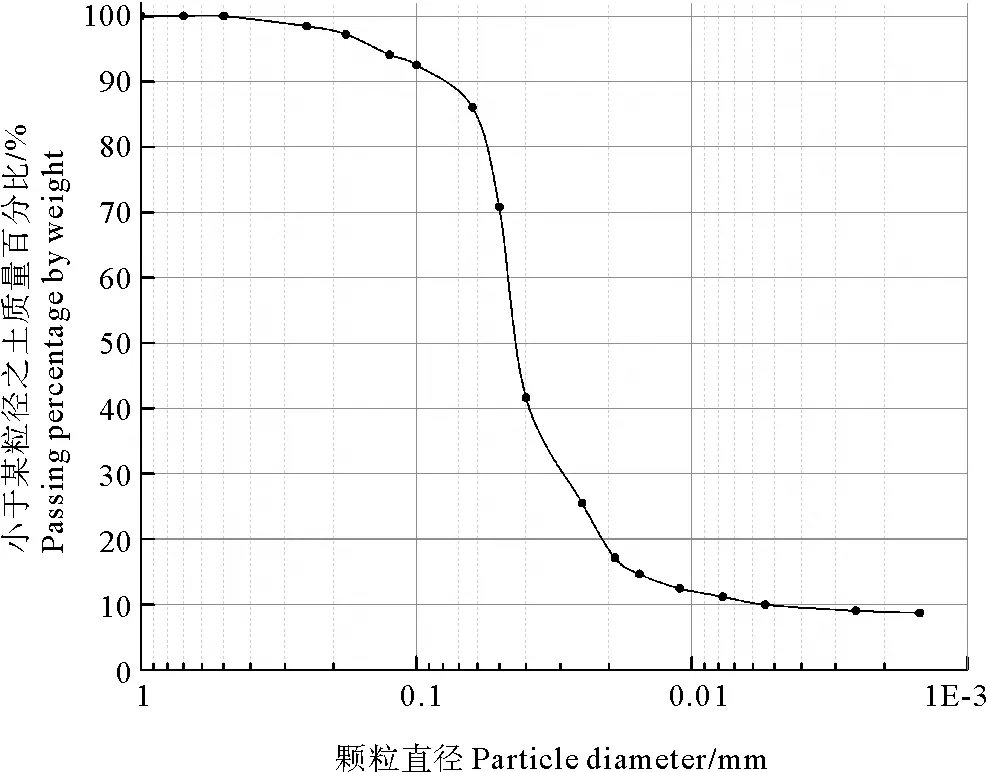
图3 试验用土级配曲线

静置固结后，开始施加波浪作用。首先施加波高5.2 cm的波浪120 min，随后施加波高11.7 cm的波浪100 min，随后施加波高17.0 cm的波浪。100 min后，液化深度达到30 cm时，保持17.0 cm波高不变，将密度球两端的尼龙线搭在两侧滑轮上，将密度球从两支架的中间位置放入水体中，释放两边使其自由振荡，激光位移传感器实时测量激光反射板的位移，同时用奥地利生产的Dewe-43型数据采集仪以50 Hz的频率实时记录。350 s后，激光反射板不再明显振动，密度球沉降结束。将密度球取出，使用自制土体采样器插入底床，取不同液化深度的土样并计算平均密度，用于粘滞系数的计算。

利用激光位移传感器数据计算出左右两侧线长a、b。根据式(10)、(11)计算试验中密度球在各个时刻的位置(x,y)，由此绘制密度球在液化土中的位移随时间的变化。

3 试验结果与分析讨论

试验底床在波浪作用下发生液化，通过水槽的玻璃边壁观察到液化土颗粒随波浪做椭圆轨迹的运动，椭圆轨迹的长短轴随深度增大而减小，在液化底界面处，土颗粒仅沿液化底界面做往复运动。密度球释放之后，两侧的激光反射板做一定周期的上下往复运动，该往复运动的平衡位置逐渐上移，说明液化土中的铁球做平衡位置逐渐降低的周期性运动。

Hwang等[26]总结了二十项对液化土粘滞系数的研究，根据液化土相对密度由小到大，粘滞系数从100～10 000 Pa·s不等。本研究计算理论沉降曲线时，取粘滞系数η=720 Pa·s。试验中测得ρs=3.77 g/cm3，ρl=1.86 g/cm3，代入式(5)计算密度球的理论沉降速度；将液化土面波高Hs定为实测曲线在第一个周期的最大、最小值之差，为4.3 cm，hs=30 cm，根据式(6)～(9)绘制该试验条件下密度球的两种理论沉降曲线；根据式(10)、(11)计算试验中密度球在各个时刻的位置，并进行归一化，绘制密度球的实际位移曲线，并与计算曲线进行比较。

3.1 竖直向位移-时间曲线的比较

图4所示为利用式(11)计算得到的实测竖直向位移曲线与利用式(7)计算得到的小振幅波理论竖直向位移曲线的比较。图中未给出利用式(9)计算得到的斯托克斯波理论竖直向位移曲线，原因是两种计算沉降曲线重合。

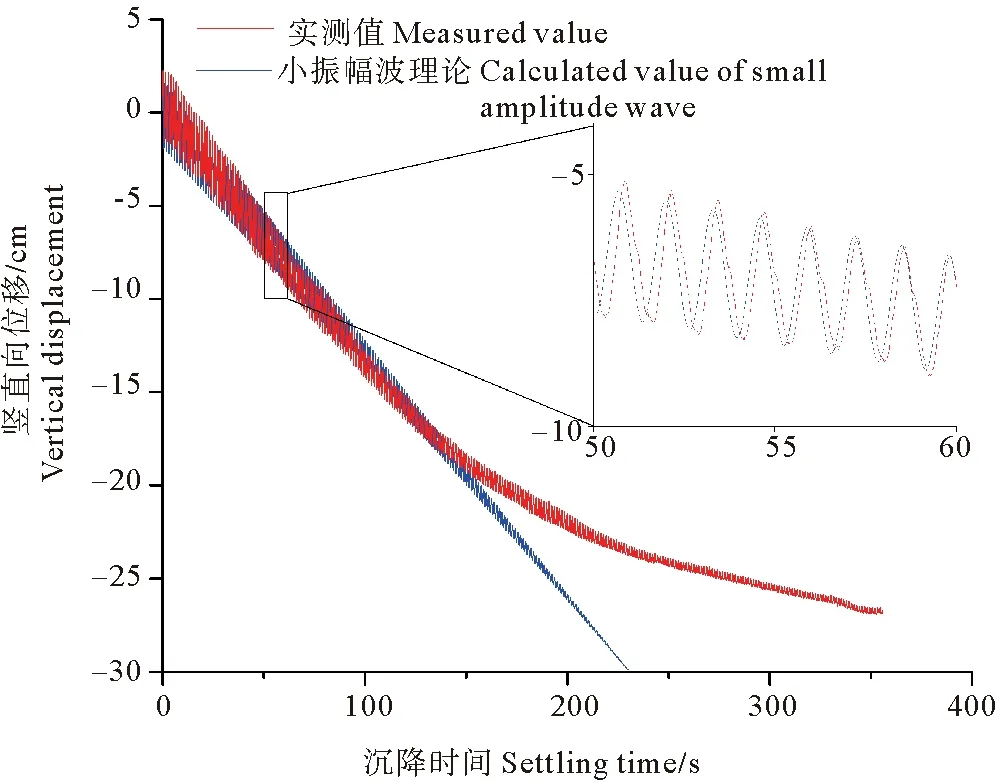
图4 竖直向位移的实测与计算值对比

整体上来看，计算竖直向位移-时间曲线从0 s持续到230 s左右结束，平衡位置从0匀速降低到30 cm，振幅从初始的3 cm逐渐衰减到0。实测竖直向位移-时间曲线在150 s前与计算曲线相似，但从150 s左右开始，其斜率逐渐减小，在350 s之后，沉降深度接近28 cm，斜率趋于0。

试验中密度球在波动液化土中做往复运动的持续时间较计算值要长。在深度达到20 cm以后，沉降速度明显减缓。可能的原因有以下两个方面：(1)液化土是一种剪切稀化流体，随着密度球沉降深度增大，其水平、竖直向振动速度减小，液化土表现出的粘滞性随之增大，超过计算时所使用的粘滞系数，故沉降速度在近底处减小。(2)液化土是一种颗粒与水的混合流体，在波动的过程中，液化土中的土颗粒发生分选，粗颗粒下沉，细颗粒上浮[27]。落球试验是在液化现象发生100 min后进行的，在这之前液化土已经发生了充分的分选，使得在接近液化底界面处的粗颗粒占比大于浅层粗颗粒占比，土体粘滞系数较浅层液化土更大。

3.2 水平向位移-时间曲线的比较

图5所示为利用式(10)计算得到的实测水平向位移曲线与利用式(6)、(8)计算得到的两种水平向位移曲线的比较，右侧为取0～5、100～105和200～205 s区间缩放所得图像。

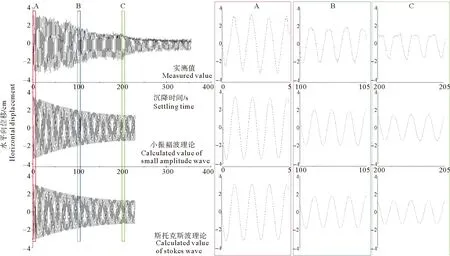
图5 水平向位移的实测与计算值对比

小振幅波理论和斯托克斯波理论的水平向位移-时间曲线在230 s左右结束，振幅相较0 s时下降约1/2；实测水平向位移-时间曲线持续到350 s，在沉降运动结束时，振幅衰减了约2/3。取0～5、100～105和200～205 s三个时间段的水平向位移曲线放大观察，发现在这三个时间段中，计算与实测水平向振幅均相差不大。

在图5中，实测密度球位移曲线随着时间的增长，其波峰有逐渐被“磨平”的趋势，呈锯齿状。其原因可能是密度球沉降过程中，尼龙线受到波浪作用，使其连接的激光反射板产生小幅度的摆动。此外，由于水槽试验中波浪周期具有一定的变动，计算得到的球体位移的峰谷值与实测值形成了相位差。

3.3 密度球运动轨迹的比较

将密度球在每一时刻的位置(x,y)绘制在坐标系中并顺序连接，获得密度球沉降运动的轨迹，实测曲线与两种计算曲线的比较见图6。

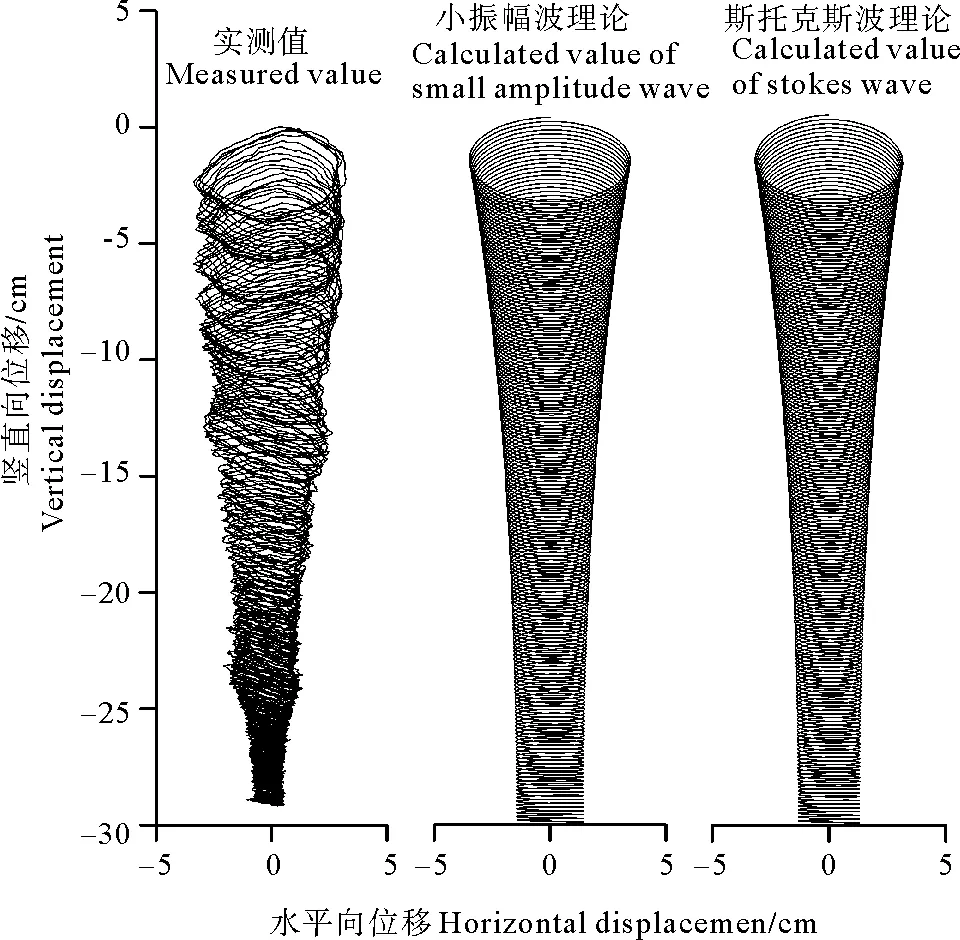
图6 实测密度球运动轨迹与两种理论计算轨迹对比

可以看到，计算的密度球沉降曲线是平滑的椭圆轨迹，每一周期密度球有一个净向下的位移，即所谓“垂向平面螺旋沉降”运动；实测轨迹为近似椭圆形，椭圆的位置随时间逐渐降低。随着密度球沉降深度增大，椭圆的长短轴衰减，椭圆逐渐变扁。到达液化底界面附近，运动近似为沿液化底界面的往返运动。

3.4 讨论

在落球试验过程中，试验球与激光反射板之间的连接线为直径0.1 mm的尼龙线。尼龙线细而牢固，在试验期间仅受到波浪冲击或滚动摩擦的轻微影响。此外，试验球去掉配重后的等效密度为3.77 g/cm3，并不远大于粉土颗粒的密度(2.65 g/cm3)，确保球体做与液化土颗粒相似的运动。

本研究中的落球试验，球体沉降运动的雷诺数为2.02×10-4，远小于1，不会发生边界层分离。因此，本研究提出的沉降位移表达式，不仅适用于球体，也适用于其他形状的块体。

4 结论

本文推导了球体在波致液化土体中的沉降位移公式，并设计试验在波浪水槽中进行了验证。主要结论如下：

(1)球体在波动液化土中做的是沉降运动与椭圆周运动的复合运动，其水平、竖直向位移可根据有限水深小振幅波和斯托克斯波的水质点位移公式改写而成。

(2)球体位置三角形控制双激光位移计测量试验结果表明，球体在液化土中会经历一定时间的匀速沉降。在接近液化底界面时，由于液化土粘滞性的改变，沉降速度减缓，并逐渐趋于0。

(3)本文推导的位移公式可以描绘出球体在波动液化土中匀速沉降阶段的竖直向位置变化、水平向振幅衰减,以及垂向平面螺旋沉降的轨迹。