基于优势演员-评论家算法的危险货物集装箱堆场安全堆存空间分配

沈阳，黄诚，宓为建

(1.上海海事大学 a.物流科学与工程研究院; b.集装箱供应链技术教育部工程研究中心，上海 201306；2.上海港城危险品物流有限公司，上海 201306)

0 引 言

危险货物作为石油化工、新材料、精细化工及高端制造业必备原材料，近年来其种类及流通不断增加，港口危险货物运输量和存储量逐年上升。危险货物集装箱(简称危货箱)作为港口危险货物运输堆存的载体，其在码头堆场中的占比逐渐增大，危货箱堆场设计堆存能力固定与堆存需求增长之间的不平衡关系日益突出。一旦危货箱堆场缺乏安全科学的堆存空间分配策略，理化性质相抵触的危货箱过于集中，就容易导致各类安全事故的发生，而且由事故引发的连锁反应和次生灾害还可能造成更加严重的后果，严重危害人身、财产和环境安全。天津港“8·12”爆炸事故即因危货箱堆场堆存策略不合理而导致箱内的硝化棉自燃引发的连环爆炸。因此，如何在保证安全性前提下，通过优化堆存空间分配策略提高危货箱堆场利用率是当前亟待解决的问题。

目前国内外学者针对传统集装箱堆场堆存空间分配问题做了大量的研究工作。CHANG等针对铁水联运集装箱码头，建立了两阶段堆存空间分配模型，第一阶段引入了一种基于启发式的模拟退火算法，第二阶段设计了一种基于滚动优化方法的新启发式算法。ZENG等以堆场集卡、起重机的运营成本与船舶的延误成本之和最小为优化目标，设计了一种启发式算法。CHEN等指出出口集装箱堆存空间分配可分为两个阶段，第一阶段采用混合整数规划模型求解贝位，第二阶段采用混合序列叠加算法求解具体堆存空间。严南南等针对集装箱堆场空间利用率不高的问题，利用数学规划方法对堆场堆存空间进行建模和求解。白治江等在兼顾岸桥和场桥负载的前提下，建立堆存空间分配的线性整数规划模型，并用滚动规划的方法解决堆场堆存空间分配问题。随着人工智能技术的日趋成熟和广泛应用，各种人工智能算法被应用于码头集装箱作业研究中。杨晓斌等提出利用蒙特卡洛树搜索算法求解新装卸工艺下陆域集疏运堆场堆存空间分配模型。XIA等运用具有优先经验回放的双深度学习网络来求解集装箱码头的装船排序决策问题。SHEN等利用深度学习网络来解决船舶配载规划问题，突破了利用在线搜索算法求解时的效率瓶颈。黄子钊等设计了基于强化学习的超启发式方法求解自动化码头出口箱箱位分配优化模型。

综上可知：在研究目标上，大部分研究均从经济效益角度(翻箱率、已用堆存空间占比、机械效率等)分析集装箱堆场堆存空间分配问题或港口其他业务，却鲜有从安全角度对危货箱堆场堆存空间分配问题进行分析;在研究方法上，大部分研究需要分阶段进行建模求解，或者仅研究单箱区、单贝位堆存空间分配，虽然降低了计算复杂度，但在实际应用上具有局限性。本文深入分析危货箱堆场安全堆存空间分配问题，并针对危货箱的理化性质、箱型结构、灭火方式、堆放位置等风险因素，提出基于安全堆存规范的危货箱堆场安全堆存空间分配模型，并采用优势演员-评论家(advantage actor-critic, A2C)算法进行求解。

1 问题描述

1.1 危货箱堆存复杂性

根据国际海事组织制定的《国际海运危险货物规则》和国家标准《危险货物分类和品名编号》(GB 6944—2012)规定，危险货物按理化性质可分成9大类20小项，分别具有易燃、易爆、腐蚀、毒害以及放射性等危险特性，每种类别的危险货物对人员及环境都会造成一定影响。危货箱堆场中的危险货物种类繁多且堆存紧凑，相互之间极易发生理化反应。如图1所示，将易燃货物与氧化性货物堆存在一起极易发生大规模火灾，有燃烧和爆炸危害的强酸和强碱应该分散堆存，毒性货物与易燃易爆货物更需要保持一定的安全隔离距离，以免发生火灾爆炸等事故导致毒性物质的泄漏。

图1 危货箱堆场安全堆存空间分配示意图

影响危货箱堆存的风险因素主要有以下几种：(1)不同危险特性的危货箱之间需满足一定的隔离要求，防止危货箱之间接触导致灾害发生；(2)同一类危险货物中危险物质成分占比不同，危险特性亦不同；(3)为降低危货箱因操作失误造成碰撞、跌落的影响，对不同类别的危货箱堆存位置(层高、列位)有着严格要求；(4)湿度、风速、风向等气候条件会影响危货箱的堆存风险以及港口处理灾害事故的应急响应能力；(5)不同箱型危货箱的不当堆叠会导致危货箱挤压破损。

人工制定危货箱堆存策略一般仅凭借经验，往往无法全面、定量考虑上述所有风险因素的影响，导致堆存风险、次生灾害风险均处于较高水平。为提高堆存安全性，只能扩大不同类别危货箱之间的隔离距离，这造成了堆存空间的极大浪费，从而使得危货箱的堆存率远低于普货箱的堆存率。

1.2 安全堆存规范

危货箱安全堆存规范的制定，旨在降低危货箱的堆存风险以及提高事故发生后的应急响应能力，以获得满足以下安全约束的最优堆存空间分配策略。具体堆存规范如下：

(1)安全隔离规范。遵循《国际海运危险货物规则》中的危货箱安全隔离表的相关规定，不相容的危货箱应分开堆存，确保满足规定的最小安全隔离距离；灭火方式相抵触的危货箱，应分区域隔离堆放，以防止对火灾事故进行施救时造成更严重的次生灾害。

(2)重大危险源临界量规范。危货箱堆场中的每个箱区均可看作是一个储存单元，为使每个箱区均保持较高的安全性，应将每个箱区的重大危险源等级均控制在第4级，即重大危险源分级指标小于10。

(3)危货箱层高堆存规范。易燃易爆危货箱最高只允许堆存2层，其他危货箱不超过3层，以防止出现火灾、泄漏等安全事故时无法进行及时有效的应急处置。

(4)潮湿环境堆存规范。装有遇潮湿易产生易燃气体的第4.3项货物，应放置在箱区最上层，以保证通风需求。

(5)堆叠规范。液化天然气罐式集装箱应分离放置，不得叠放；与其他种类危货箱叠放时，必须放置于最上层。无底梁罐式集装箱因其承压能力较差，与通用集装箱(箱内应为非易燃易爆危险货物)叠放时，应被放置到最上层，且无底梁罐式集装箱相互不得叠放。

(6)罐式集装箱与车道堆存规范。罐式集装箱不应堆放在近车道的首列箱位。罐式集装箱通常用于储存具有易燃易爆性、腐蚀性或者毒性的液体或气体，而近车道箱位相对于其他箱位而言，更容易被行驶转向中的车辆碰撞。

2 危货箱堆场安全堆存空间分配模型

2.1 符号定义

参数：为危货箱堆场箱区集合，∈；为箱区贝位集合，∈；为贝位中列位集合，∈；为贝位中层高集合，∈；为在场箱集合，∈；为计划进场箱集合，,′∈；为非最底层的层高集合；为箱区的重大危险源分级指标；为第级重大危险源分级指标临界值；为箱区初始堆存占用的箱位数；为箱区的最大箱位数；为箱区第贝第列第层的箱位与在场箱之间的实际距离；′′′′为箱区第贝第列第层的箱位与箱区′第′贝第′列第′层的箱位之间的实际距离；为安全隔离表规定的进场箱与在场箱之间的安全隔离距离；′为安全隔离表规定的进场箱与进场箱′之间的安全隔离距离；为灭火方式相抵触情境下进场箱与在场箱之间的安全隔离距离；′为灭火方式相抵触情境下进场箱与进场箱′之间的安全隔离距离；为进场箱与在场箱之间的最小安全隔离距离，=max(,)；′为进场箱与进场箱′之间的最小安全隔离距离，′=max(′,′)；为箱区的剩余安全堆存空间因数，用于估计箱区剩余堆存空间中安全堆存空间占比，∈[0,1]。

决策变量：，为0-1变量，如果进场箱被分配到箱区第贝第列第层则取值为1，否则为0。

2.2 目标函数

(1)

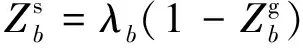
(2)

由此可得目标函数和如下，其中：,′∈;,′∈;∈;,′∈;,′∈;,′∈。

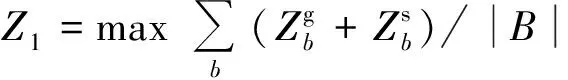
(3)

(||||+||)

(4)

2.3 约束条件

下述表达式中除特殊说明外，有：,′∈;,′∈;∈;,′∈;,′∈;,′∈。

(5)

(6)

(7)

(8)

′,≠′

(9)

(10)

(11)

(12)

(13)

(14)

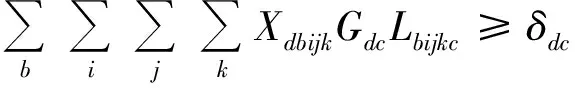
(15)

′,≠′

(16)

(17)

(18)

式(5)表示一个进场箱仅占用一个箱位；式(6)表示一个箱位只能堆存一个进场箱；式(7)表示箱位分配要满足非悬空约束；式(8)和(9)分别表示进场箱与在场箱、进场箱之间需满足安全隔离表规定的安全隔离距离约束；式(10)表示待分配危货箱需满足所在箱区的重大危险源临界量约束，重大危险源等级设为第4级(安全性最高)；式(11)和(12)分别表示易燃易爆危货箱及非易燃易爆危货箱的层高约束；式(13)表示第4.3项危险货物的潮湿环境约束；式(14)表示液化天然气罐式集装箱的堆叠堆存约束；式(15)和(16)分别表示灭火方式相抵触的进场箱与在场箱、进场箱之间均需满足一定的安全隔离距离约束；式(17)表示无底梁罐式集装箱堆叠堆存约束；式(18)表示罐式集装箱与车道的堆存约束。

3 A2C算法

A2C算法是一种基于策略的强化学习算法，它将每次空间分配后安全堆存空间利用率和安全指数的增量作为环境反馈的奖励，以累计奖励最大为目标智能选择分配动作。该算法包括两个模型网络，Actor 表示策略模型网络，Critic 表示价值模型网络，通过Actor直接输出策略函数，通过Critic对输出动作进行评价。该算法能够高效地求解危货箱堆场安全堆存空间分配这类有着大规模离散动作空间的优化问题，避免了需要计算所有动作值的复杂性。同时，该算法引入并行训练机制，利用多线程并行独立训练，能消除数据的相关性，提高神经网络的收敛速度和收敛稳定性。

3.1 算法架构

为达到安全堆存空间利用率和安全指数同时优化的目标，将危货箱堆场环境建模为交互环境，将危货箱堆场安全堆存空间分配问题转化为智能体与环境的交互问题，利用Actor和Critic的反复训练和学习，达到最大奖励。算法架构见图2。将堆场堆存状态输入Actor后，得到相应的堆存空间分配动作、奖励和下一时间步的状态+1。Critic通过值评价动作的好坏，并利用计算出的时间差分误差更新Actor参数。A2C算法利用优势函数取代Critic中的长期回报，使得网络参数在梯度更新时有更低的方差。同时，A2C算法具有多线程并行训练机制，工人线程网络是全局网络的预处理子网络，全局网络通过整合所有工人线程网络学习到的经验(神经网络参数)，用于最终堆存空间分配动作决策。算法训练时并行创建多个工人线程网络；工人线程网络首先从全局网络中同步已有经验；每个工人线程网络进行独立采样学习，得到堆存空间分配历史经验；在所有工人线程网络都计算出对应的损失函数后，将梯度上传给采集器；采集器汇总所有梯度求平均，并将平均梯度同步更新给全局网络进行网络参数更新，从而极大地提高神经网络训练学习的速度。

图2 A2C算法架构

3.2 算法设计

构建马尔科夫决策过程(Markov decision process，MDP)：

(1)状态。在时间步的状态包含在场箱堆存状态和进场箱状态。

(2)动作。在时间步，进场箱待分配空间时，将环境状态经过预处理后输入到Actor，Actor会输出一个动作作为进场箱的最优堆存空间分配动作，即在当前堆场堆存状态下某个进场箱应分配到哪个箱位(决策变量)，表达式如下：

=,∈

其中：为被分配到的有效堆存空间，即有效箱位；为有效箱位集合。

危货箱堆场每个箱位均对应一个分配动作，若堆场堆存空间(即箱位)有2 000个，日进场箱量为150个，则理论动作空间大小(决策变量范围)为2 000(≈10)。可以看出，如不对动作进行约束剪枝，算法的计算复杂度极大。

(3)奖励。将目标函数(式(3)和(4))转化为MDP的表述，即优化目标为时间段内的累计安全堆存空间利用率和安全指数，其中={|∈[0,]}。在时间步的安全堆存空间利用率1和安全指数2可表示为

式中：为在时间步分配的危货箱；、和分别为所在箱区的最大箱位量、已占用箱位数以及剩余安全堆存空间因数;为在时间步的在场箱集合。

对这两个目标进行归一化处理及加权处理后，得到优化目标：

=1+2

其中：、分别为1和2的权重，其取值根据实际堆存过程中对两个目标的重视程度决定；、分别为指标的归一化参数。

将优化目标的增量Δ作为奖励判定的依据：

=Δ=--1

若Δ为正，则说明堆存空间分配动作给智能体带来了更高的指标收益，此时给予奖励；若Δ为负，则说明堆存空间分配动作带来了负面效果，此时给予惩罚。

A2C网络结构进一步设计如下：

(1)输入状态空间重构。堆场三维空间比围棋棋盘格二维空间多了一个垂直方向的维度，即堆存层高，因此将堆场每一层的危货箱堆存空间状态按实际空间坐标位置处理为一个图像张量，并且通过对图像张量的补零操作处理非集装箱堆存空间(例如箱区间的车道等)状态。假定危货箱堆场的层高限制为层，则堆场堆存空间状态可以被处理成+1个图像张量，其中前个图像张量分别表征在时间步的每一层危货箱堆存空间状态，第+1个图像张量表征在时间步的进场箱状态。

(2)动作约束。在强化学习算法中，对于不可行(不符合约束条件)动作通常可以通过制定相应的惩罚函数去抑制，但堆存空间分配问题中动作空间很大(数千至数万个可选动作)，大量无意义的分配动作参与计算会使得训练迭代的代价很大。因此，算法将不可行动作通过掩码(Mask)进行屏蔽，从而实现对动作空间的剪枝，使得其迭代速度更快且更容易收敛。

Actor动作约束流程如下：①将危货箱堆存空间状态和进场箱状态输入到卷积神经网络(convolutional neural network，CNN)，经过CNN的卷积、激活及全连接后得到Actor的输出，即安全堆存空间分配动作的值向量=(,,…,-1,)；②根据模型约束条件生成分配动作掩码向量，将向量中可行动作对应的值设为1，不可行动作(如违反隔离关系、超高堆存等的动作)对应的值设为0，假定=(1,0,…,0,1)；③通过与数乘计算，将不可行动作的值屏蔽，得到新的值向量，′=(,0,…,0,)；④采用Softmax策略获得堆存空间分配动作概率分布函数，并依照动作概率选择对应动作执行。动作约束过程可用下式表示：

(|;)=Softmax(′)

式中：(|;)为堆存空间分配动作概率分布函数，表示在状态下全部动作的概率分布；为Actor参数。

(3)网络训练和更新。A2C算法结合了演员-评论家(actor-critic，AC)算法与优势函数。Actor使用策略函数(,)来输出动作概率并选择动作。AC算法的策略函数的目标是最大化奖励，策略梯度可表示为

∇()=(∇log(|;)(,))

其中：()表示目标函数；策略函数(|;)用一个神经网络来近似表示在状态下选择动作的概率；价值函数(,)表示在状态下选择动作的未来累计奖励期望。

AC算法的策略梯度中的函数需要在交互中不断学习去逼近真实值，这意味着梯度更新过程会出现噪声，即高方差，从而导致学习速率减缓。为解决这一问题，A2C算法采用奖励减去基线函数的方式学习策略函数。定义优势函数(评价当前状态动作值函数相对于平均值的优势)为

(,)=(,)-()

式中：()为状态值函数。

A2C算法的策略梯度为

∇()=(∇log(|;)(,))

Actor参数的更新公式如下：

←+∇log(|;)((,)-())

式中：为Actor本地梯度更新学习率。

在实际应用中，为简化A2C算法，可对(,)进行估计：

(,)≈+(+1)

式中：为环境奖励回报值；为用于计算累计奖励值的折扣因子。

根据时间差分误差的定义，时间差分误差即为优势函数(,)的无偏估计。因此，Critic参数的梯度可采用均方误差作为损失函数进行更新，损失函数为

4 实验及结果分析

4.1 数据集

实验所使用的进场箱数据为上港集团危货箱堆场的真实业务数据。该危货箱堆场面积约12万m，危货箱年吞吐能力约20万TEU，核准可堆存箱量4 600 TEU。如表1所示，该数据集按危险货物类别可划分为8大类19小项(除第7类放射性物质)，共有10万条自然箱数据，其中第3类易燃液体、第8类腐蚀品、第9类杂项危险品由于应用广泛，样本占比分别达到39.22%、12.85%和21.19%，而第1类爆炸品因监管要求直装直取，因此样本占比仅为0.86%。

表1 进场箱训练数据

4.2 参数设置

基于上港集团危货箱堆场布局进行设置，详细布局见图3。危货箱区数量||=57，单个箱区规模(贝×列×堆)从3×4×3到29×5×3不等，最大堆存层高=3。假定危货箱随机到达，初始危货箱空间分布也随机生成。本文采用PyTorch+gym实现A2C算法。训练过程使用Softmax策略表示策略函数，采用Adam算法作为梯度优化器，Actor和Critic本地梯度更新学习率分别为=0.001，=0.001，熵系数=0.01, 折扣因子=0.95。A2C算法使用两个CNN模型逼近策略函数(|)和状态值函数();每个网络模型共有5层，其中有3个卷积层和2个全连接层;为避免丢失在场箱信息，不设池化层对特征进行压缩。输入状态空间层数3(最大堆存层高为3)以及1个图像张量。

图3 实验堆场危货箱区平面布局

4.3 实验结果分析

4.3.1 性能分析

为验证本文算法的性能，设计10组实验，见表2，其中：第1～8组分别选取一类危货箱，每组箱量分别为50；第9组为每类危货箱数量均为10的小规模算例;第10组为每类危货箱数量均为40的大规模算例。

表2 10组实验中各类危货箱的自然箱量

利用A2C算法求解的危货箱堆场安全堆存空间分配结果见表3。从表3可知：本文算法分配结果总体表现较好，安全堆存空间利用率和安全指数的优化结果均超过人工水平；由于第3类易燃液体、第8类腐蚀品和第9类杂项危险品事故风险较低，综合优化效果最好；由于第1类爆炸品、第6类毒性物质与其他类别危险货物在理化性质上存在较大的不相容性，并且事故危害较大，所以综合优化效果较差；由于样本及计算复杂性影响，对大规模算例的优化结果要略劣于对小规模算例的优化结果，但综合优化效果亦超过人工水平，具备实际应用价值。

表3 分配结果对比

4.3.2 算法对比分析

由于危货箱堆场堆存空间分配模型计算规模巨大、约束较多，往往难以通过最优化方法找到最优解。因此，本节采用模拟退火(simulated annealing, SA)算法和遗传算法(genetic algorithm, GA)这两种传统智能算法与A2C算法进行对比分析，验证本文算法的综合性能。SA算法主要参数设置：初始温度500 ℃，终止温度1×10℃，温度衰减系数0.98，每个温度迭代次数100。GA主要参数设置：交叉概率0.8，变异概率0.05，迭代次数500。

图4为在样本规模为50的算例中，不同已用堆存空间占比下各算法的目标优化结果。本文算法中安全堆存空间利用率和安全指数的权重均为 0.5，即重要程度相等。根据图4的实验结果可以得出：本文采用的A2C算法能够获得较优的安全堆存空间分配策略，在不同已用堆存空间占比下其安全堆存空间利用率和安全指数均超过SA算法和GA的。当已用堆存空间占比超过50%时，本文算法性能优越，不仅能满足日益增长的危货箱堆存需求，还能有效降低堆存风险。在已用堆存空间占比为90%时，在剩余空间中所有算法均难以获取更多的安全堆存空间。同时，随着已用堆存空间占比的增加，可用堆存空间逐渐减少，各类算法及人工分配的性能均出现不同幅度的下降，但本文算法下降幅度最低，说明本文算法在不同环境状态下稳定性良好。

a)安全堆存空间利用率

4.3.3 收敛性分析

图5为本文A2C算法的收敛曲线，纵坐标为每次迭代训练时得到的平滑奖励。由于刚开始时-贪婪策略的探索概率较大，安全堆存空间分配经常出现较大的失误，所以安全风险升高。随着算法的不断学习，当迭代次数超过100 000次后，安全堆存空间分配策略逐渐改善，并最终收敛获得最优解。

图5 A2C算法的收敛曲线

5 结 论

本文针对基于安全堆存规范的危货箱堆场安全堆存空间分配问题进行研究，以安全堆存空间利用率和安全指数作为优化目标，构建了多目标优化模型，并设计A2C算法进行求解。通过对不同规模算例的分析，验证了本文算法能够充分考虑危货箱的理化性质、箱型结构、灭火方式等风险因素，保证了不同工况下均能获得超越人工水平的空间分配策略，使得港口危货箱的堆存安全性及堆场利用率得到显著提高。同时，在性能表现上亦优于其他传统智能算法。该方法不仅能够有效降低港口危货箱的堆存风险，提高危货箱灾害应急响应能力以及减少次生灾害的影响，还能够满足港口危货箱吞吐量持续增长的需求，对港口物流行业解决危货箱安全堆存问题具有借鉴意义。