线性子空间上求解AXB+CXD=F的最小二乘问题的迭代算法

周海林

(南京理工大学 泰州科技学院,江苏泰州 225300)

§1 引言

约束矩阵方程的最小二乘问题是指矩阵方程的最小二乘解需要满足某一约束条件.不同的约束条件或不同的矩阵方程,就得到不同的约束矩阵方程的最小二乘问题.

约束矩阵方程的求解具有重要的理论意义和很高的应用价值.来源于系统与控制理论中提出的矩阵方程AXB+CXD=F,在特征结构配置[1],观测器设计[2]和带有输入约束的系统控制[3]等方面起着重要的作用,也受到矩阵论和数值分析学者的关注,取得了一些成果[4-11].这些文献主要应用广义逆,奇异值分解和广义奇异值分解,得到了矩阵方程的解的充要条件及解析表达式.

迭代法是求解约束矩阵方程的另外一种方法,尽管它不能给出通解表达式,但在不考虑舍入误差的情况下,能通过有限步迭代得到满足给定约束条件的解.应用共轭梯度法,文[12-14]构造迭代算法分别求解了矩阵方程AXB+CXD=F的一般解,对称解和在任意线性子空间约束下的解.文[15-17]研究了Hermitian解和极小范数最小二乘Hermitian解.更多求解矩阵方程AXB+CXD=F的迭代算法可参考文献[18-28].

记Rm×n表示m×n实矩阵集合,AT表示A的转置矩阵.对任意的矩阵A,B∈Rm×n,定义矩阵内积〈A,B〉=tr(BTA),则由它诱导的范数为Frobenius范数,即

本文主要考虑下面两个问题.

问题I给定矩阵A ∈Rm×s,B ∈Rt×n,C ∈Rm×s,D ∈Rt×n,F ∈Rm×n,任意线性子空间R ⊆Rs×t,求X*∈R,使得

相应地,问题I和问题II的解称为矩阵方程AXB+CXD=F满足线性子空间R约束条件下的最小二乘解和最佳逼近解.本文应用共轭梯度法,结合线性投影算子,将负梯度到所求线性子空间上的投影矩阵作为迭代过程中下一步的更新矩阵,给出迭代算法,求解了矩阵方程AXB+CXD=F在任意线性子空间上的最小二乘解及其最佳逼近.

本文以下内容安排如下:§2构造迭代算法求解了问题I ;§3应用问题I的算法进一步求解了问题II;§4给出两个数值例子证实了算法的有效性;§5对全文进行了小结.

§2 迭代求解问题I

定义2.1对矩阵M,N ∈Rm×n,若〈M,N〉=0,则称矩阵M,N相互正交.

对任意的线性子空间R ⊆Rs×t,其正交补空间R⊥是存在唯一的,且有Rs×t=R ⊕R⊥.在Rs×t上定义线性投影算子FR:Rs×t -→R.

显然,对任意的X∈Rs×t和任意的S∈R,有〈X,S〉=〈FR(X)+FR⊥(X),S〉=〈FR(X),S〉成立.

引理2.1设S是一个有限维内积空间,M是S的一个子空间,且M⊥是M的正交补空间.则对于任意给定的向量s ∈S,必存在着唯一的向量m0∈M,使得

其中‖·‖是内积空间S所定义的范数,并且m0∈M是唯一的极小化向量的充要条件是(sm0)⊥M,即(s-m0)∈M⊥.

引理2.2设线性子空间R ⊆Rs×t,FR是从Rs×t到R的线性投影算子,记R*=F -(AX*B+CX*D),则X*是矩阵方程AXB+CXD=F在线性子空间R上的最小二乘解的充要条件是FR(∇f(X*))=0.

证定义集合

显然,L为线性子空间.假设矩阵X*∈R,记F*=AX*B+CX*D,则F* ∈L.由引理2.1知,X*是矩阵方程AXB+CXD=F的最小二乘解,当且仅当

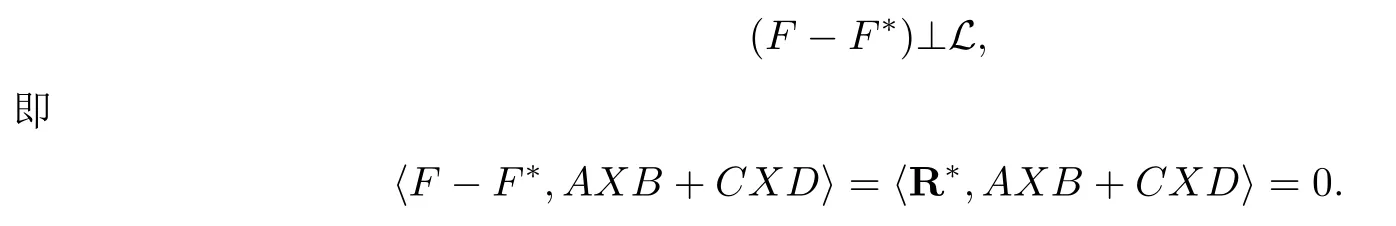
另外对任意的X ∈R有

从而FR(ATR*BT+CTR*DT)=0,即有FR(∇f(X*))=0,故引理得证.

应用共轭梯度法,结合线性投影算子,本文构造如下迭代算法.

算法I

输入矩阵A ∈Rm×s,B ∈Rt×n,C ∈Rm×s,D ∈Rt×n,F ∈Rm×n,任取初始矩阵X0∈R.

(1) 计算

(2) 如果Pk=0,停止;否则进行下一步.

(3) 计算

(4) 转回到(2).

显然,Pi=FR(ATRiBT+CTRiDT)=FR(-∇f(X)|X=Xi)∈R,Qi ∈R,Xi ∈R,i=0,1,2,3,···.

此外在步骤(3)中

引理2.3若算法I在第k步迭代尚未停止,则迭代过程中产生的Pi,Pj,Qi,Qj,(i,j=0,1,21),有

证用数学归纳法证明.

由于对任意矩阵M,N∈Rm×n,有〈M,N〉=〈N,M〉,故只需证明0≤i ＜j ≤k时结论成立即可.

首先注意到

对t=1,由算法I有

设(3)式对t=s(1≤s ≤k-1)成立,即

i,j=0,1,21,则当t=s+1时,由算法I,与(4)式相类似的证明有

由算法I,与(5)式相类似的证明可得到

对i=1,2,3,···,s-1,注意到

由算法I得到

因此对t=s+1(3)式成立.

由数学归纳法知,引理2.3得到了证明.

注引理2.3中,若算法I在第k步迭代尚未停止,则意味着当i=0,1,2,···,k时,有Pi0,从而αi0且AQiB+CQiD0.下面予以说明.

若AQiB+CQiD=0,则

从而有Pi=0,故AQiB+CQiD0.

引理2.3表明,由算法I产生的矩阵序列P0,P1,P2···在矩阵空间R上是相互正交的,从而必定存在一个正整数r ≤st,使得Pr=0,从而得到下面的定理.

定理2.1在不考虑舍入误差的情况下,对任意给定的初始矩阵X0∈R,算法I可在有限步内计算出问题I的解.

引 理2.4若是问题I的解,则问题I的任意解均可表示为,其中X∈R且满足AXB+CXD=0.

从而‖AXB+CXD‖2=0,即AXB+CXD=0.

定理2.2若取初始迭代矩阵X0∈FR(ATHBT+CTHDT),其中H是Rm×n中的任意矩阵,或者特别地,令X0=0s×t,则由算法I,通过有限步迭代可以得到问题I唯一的极小范数解.

证定义集合

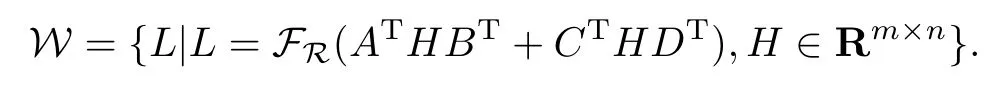
显然W为线性子空间.若令初始迭代矩阵X0∈W,则由算法I得到的迭代更新矩阵Xk∈W.(k=1,2,···) 由算法I和定理2.1知,经有限步迭代可得到问题I的解X*,且X*∈W.即存在H*∈Rm×n,使得X*=FR(ATH*BT+CTH*DT).

由引理2.4知,问题I的任意解可以表示为X*+X,其中X∈R,且满足AXB+CXD=0.又

故X*为问题I的极小范数解.不难验证问题I的解集SE为非空闭凸集,其极小范数解存在且是唯一的.所以X*也是问题I的唯一极小范数解.

§3 问题II的解

因为问题I的解集SE是非空闭凸集,故问题II的解存在且唯一.对问题II中给定的∈Rs×t,由于X∈R,因此

§4 数值例子

以下例子通过编写M文件(见附录solution.m)在Matlab R2017a(运行环境: 64位Win7操作系统,Intel(R) Core(TM) i3-2350M CPU @ 2.30GHz处理器,4.00GB内存) 上运行,所得结果证实了该算法的有效性.

例1在本例中将R取为n阶实对称矩阵集合,显然,R为线性子空间.

在Rn×n上定义如下线性投影算子

由于计算误差的影响,在具体的迭代过程中,Pi(i=0,1,2,···)一般不会等于零,迭代次数也不一定完全符合理论所需次数.因此任取充分小的ε,譬如ε=1.0e-010(Matlab程序运行结果中显示,意思是1.0×10-10),当‖Pk‖＜ε=1.0e-010时,停止迭代,视Xk为问题I和问题II的解.

为了保持重复试验中结果的一致性,在Matlab中输入随机矩阵之前,需要将随机发生器置于相同的初始状态.

(I) 不妨在Matlab中将随机发生器置于状态rand(’twister’,0),让X0=rand(5)(注: rand(5)在Matlab中指的是各元素来自[0,1]区间且服从均匀分布的5阶随机矩阵).

且‖P17‖=2.7559e-11＜ε,‖X17‖=1.0889,‖R17‖=14.9474,耗时t=0.0050秒.

若取初始迭代矩阵X0为5阶零矩阵,经过13(＜st=25)步迭代,得到问题I的唯一极小范数解

且‖P13‖=4.9355e-11＜ε,‖X13‖=0.3178,‖R13‖=14.9474,耗时t=0.0099秒.

在例1中,记迭代次数为k,定义r(k) :=log10‖Pk‖.下面图1是r(k)与迭代次数k的变化曲线图,它间接显示了梯度投影矩阵范数‖Pk‖与迭代次数k的变化情况.

图1 例1中r(k)曲线图

图1中,曲线y1和y2分别描述了求解问题I 时,初始迭代矩阵X0分别为rand(5)和05×5时函数r(k)的变化情况,曲线y3描述了求解问题II 时函数r(k)的变化情况.图1也显示算法I在求解例1中的问题I和II时是可行的,有效的.

例2记R表示所有n阶主对角线元素为零的矩阵构成的集合.显然R为线性子空间.

对任意的矩阵X=(xij)∈Rn×n,令

显然X=X1+X2,且这样的X1和X2唯一,又,故在Rn×n上定义线性投影算子

为了讨论方便,不妨让本例中的矩阵A,B,C,D,F,分别为例1中的矩阵,n=5.

(I) 在Matlab中将随机发生器置于状态rand(’twister’,0),不妨让X0=rand(5),取初始迭代矩阵X0=X0-diag(diag(X0)),应用算法I,经过16(＜st=25) 步迭代,得到矩阵方程AXB+CXD=F在子空间R上的一个最小二乘解

且‖P16‖=4.6810e-11＜ε,‖X16‖=1.2567,‖R16‖=14.9474,耗时t=0.0011秒.

若取初始迭代矩阵X0为5阶零矩阵,经过12(＜st=25) 步迭代,得到问题I的一个极小范数解

且‖P12‖=1.8840e-12＜ε,‖X12‖=0.2545,‖R12‖=14.9474,耗时t=0.0039秒.

显然,X16∈R,X12∈R,‖X12‖＜‖X16‖,‖R16‖=‖R12‖.

在例2中,同样地,定义r(k) :=log10‖Pk‖.下面图2是r(k)与迭代次数k的变化曲线图,它间接显示了梯度投影矩阵范数‖Pk‖与迭代次数k的变化情况.

图2 例2中r(k)曲线图

图2中曲线y1和y2分别描述了求解问题I时,初始迭代矩阵X0分别为rand(5)和05×5时函数r(k)的变化情况,曲线y3描述了求解问题II时函数r(k)的变化情况.图2也显示算法I在求解例2中的问题I和II时是可行的,有效的.

§5 结论

应用共轭梯度方法和线性投影算子,讨论了矩阵方程AXB+CXD=F在任意线性子空间R约束下的最小二乘解问题.与最优化中将负梯度在边界上的投影作为迭代点前进方向的梯度投影法不同的是,本文将矩阵函数的负梯度投影到所求线性子空间(矩阵空间)上的矩阵作为迭代过程中下一步的更新矩阵,以此来保证更新矩阵自动满足线性子空间的约束.可以证明,在有限的误差范围内,所给算法经过有限步迭代可得到矩阵方程AXB+CXD=F的最小二乘解,极小范数解及相应的最佳逼近.最后分别以实对称矩阵和主对角线元素为零的矩阵为对象进行数值实验,进一步证实了算法的有效性.一般地,在Rs×t上定义线性投影算子F,就得到相应的线性子空间R.因此,对于某线性子空间,只要定义相应的线性投影算子,文中的迭代算法就可以用来求解矩阵方程AXB+CXD=F在该线性子空间约束下的最小二乘问题.

致谢审稿人提出的意见和建议极大地促进了对原稿件的提升和完善,作者在此表示衷心的感谢.