知识库的相对约简与拓扑约简
2022-09-29吴国俊徐罗山
吴国俊,徐罗山
(扬州大学 数学科学学院,江苏扬州 225002)
§1 引言
粗糙集理论[1]首先由Pawlak提出,是用于处理不确定性知识的数学工具.在粗糙集理论中,知识约简是重要的课题,也是获取知识的重要步骤.论域U上的知识指U上的某个等价关系,知识库指的是U上的一族等价关系,文献[2]论述了知识库的多种约简理论.赵静,徐罗山在文献[3]中研究了知识库的知识约简和知识表达系统的属性约简的转化和联系.王长忠等在文献[4]中把知识库推广为关系信息系统,它实际为U上的一族二元关系.文献[5]则把U上的任一子集族称为一个抽象知识库.本文强调与抽象知识库的区别,把关系信息系统仍称为知识库.李旭等在文[6]中定义了相对不可区分关系约简和相对区分关系约简.本文对知识库提出相对约简概念,给出有限知识库相对约简的求法.文献[7-13]将拓扑学方法引入到粗糙集的研究中,提出了关系诱导拓扑,其中文献[12-13]利用拓扑学方法讨论了知识的多种约简.本文借助关系诱导拓扑提出拓扑约简的概念,探讨交约简,相对约简和拓扑约简的关系及其求法.
§2 预备知识
本文用P(U)表示U的幂集,U上的恒等关系△={(x,x)|x ∈U},又称为对角关系.用|·|表示集合的基数,无特别说明,约定|U|>1.
设R是U上的二元关系.则序对(U,R)称为一个广义近似空间.对x ∈U,记Rs(x)={y ∈U |xRy}与Rp(x)={y ∈U |yRx}.U上自反又传递的二元关系称为一个预序.
定义2.1[7-11]广义近似空间(U,R)中的下近似算子和上近似算子分别定义为:P(U)→P(U)使得
引理2.1[8]设(U,R)是广义近似空间,则为U上的Alexandrov拓扑,并称该拓扑为(U,R)的关系诱导拓扑.
定义2.2[11]设R是论域U上的二元关系,包含R的最小预序称为R的预序闭包,记为p(R).
注2.1容易验证(1)R ⊆p(R)=p(p(R))且p(R)=△∪R ∪R2∪R3∪···.
(2) 设R,Q是论域U上的二元关系,若Q ⊆R,则p(Q)⊆p(R).
命题2.1设R1,R2是U上的二元关系,R1⊆R2.则p(R1)=p(R2)当且仅当R2⊆p(R1).
证必要性: 因R2⊆p(R2),故由p(R1)=p(R2)知,R2⊆p(R1).
充分性: 因R1⊆R2⊆p(R1),故由注2.1知p(R1)⊆p(R2)⊆p(p(R1))=p(R1),从而p(R1)=p(R2).
引理2.2[11]设(U,R1),(U,R1)是两广义近似空间,则TR1=TR2当且仅当p(R1)=p(R2).
定义2.3[14](1) 设R是U上的一族二元关系.则(U,R)称为U上的知识库,也简称R是U上的知识库.交集∩R=∩P ∈R P称为R的不可区分知识,记作ind(R).(2) 设R是U上的知识库,Q ⊆R且.若ind(Q)=ind(R)且对Q的任一非空真子集Q0,ind(Q)ind(Q0),则Q称为R的交约简.R的全体交约简用red(R)表示.
(3) 设R是U上的知识库.当|R|>1时,称集族{R ∈R|ind(R-{R})ind(R)}为R的核,记为core(R).当|R|=1时,约定core(R)=R.
§3 知识库的相对约简与RM-区分矩阵
本节给出知识库相对约简与RM-区分矩阵的概念,并研究它们的相关性质.关于有限偏序集的结论可参见文献[15].
定义3.1设R是U上的知识库,Q是U上的二元关系且ind(R)⊆Q.若存在使ind(P)⊆Q,且对P的任一非空真子集P0,有,则称P是R相对于Q的交约简,简称Q-相对约简.R的全体Q-相对约简可用redQ(R)表示.
注3.1由定义2.3和3.1知R的交约简就是R的ind(R)-相对约简,即red(R)=redind(R)(R).这说明交约简是特殊的相对约简.当该定义中涉及的二元关系均为等价关系且论域U是有限集时,定义3.1中R的Q-相对约简就是文[2]中Q关于R相对依赖度为1的Q-相对约简.
命题3.1设R是有限集U上的知识库,Q是U上的二元关系且ind(R)⊆Q,则R存在Q-相对约简,即redQ(R).
证作A={P ⊆R |ind(P).因R ∈A,故.因(A,⊆)是非空有限偏序集,故其每个链L都存在最小元.由Zorn引理知(A,⊆)存在极小元P0,则ind(P0)⊆Q.又由P0的极小性知P0的任一非空真子集均不含于Q.这说明P0∈redQ(R).
注3.2命题3.1的证明过程实际上给出了求相对约简的极小元方法: 构造偏序集A={P ⊆R|ind(P),求出(A,⊆)的所有极小元,它们恰好是R的全体Q-相对约简.对于论域无穷的情形,容易举例说明(相对)约简不一定存在.
定义3.2设R是U上的知识库,Q是U上的二元关系且ind(R)⊆Q.当|R| >1时,若存在R ∈R使,则称R为R的Q-相对核心元素,称为R的Q-相对核,记为coreQ(R).当|R|=1时,约定coreQ(R)=R.
命题3.2设R是U上的知识库,Q是U上的二元关系且ind(R)⊆Q.则coreQ(R)⊆core(R).
证当|R|=1时,显然.下面设|R| >1.若R ∈coreQ(R),则因ind(R)⊆Q,故ind(R-{R})ind(R),从而R ∈core(R).于是coreQ(R)⊆core(R).
定理3.1设R是有限集U上的知识库,Q是U上的二元关系且ind(R)⊆Q,则coreQ(R)=∩redQ(R).
证当|R|=1时,显然.下面对|R| >1先证明coreQ(R)⊆∩redQ(R),用反证法.若存在R ∈coreQ(R)使R/∈∩redQ(R),则存在Q ∈redQ(R)使R/∈Q.于是Q ⊆R-{R},从而ind(R)⊆ind(R -{R})⊆ind(Q).由Q ∈redQ(R)知,ind(Q)⊆Q,由ind(R -{R})⊆ind(Q)得ind(R-{R})⊆Q,这与R ∈coreQ(R) 矛盾.再证明∩redQ(R)⊆coreQ(R),用反证法.若存在R ∈∩redQ(R)使R/∈coreQ(R),则ind(R-{R})⊆Q.任取Q0∈redQ(R-{R}),可推得Q0∈redQ(R)且R/∈Q0,这与R ∈∩redQ(R)矛盾.综上所证,coreQ(R)=∩redQ(R).
定义3.3设R是上知识库,Q是U上二元关系且ind(R)⊆Q,∀xi,xj ∈U,记
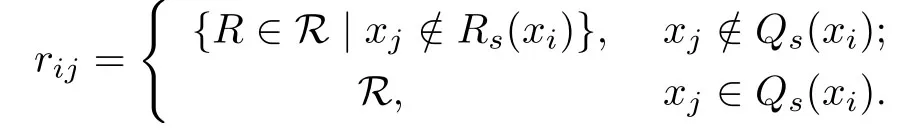
则称矩阵DQ(U,R)=(rij)n×n是R相对于Q的RM-区分矩阵.
命题3.3设R是上的知识库,Q是U上的二元关系且ind(R)⊆Q,DQ(U,R)是R相对于Q的RM-区分矩阵.若,则ind(P)⊆Q当且仅当∀rij ∈DQ(U,R),P∩rij Ø.
证必要性: 对任一rij ∈DQ(U,R),若xj ∈Qs(xi),则rij=R,此时P ∩rij=.若xj/∈Qs(xi),则(xi,xj)/∈Q.由ind(P)⊆Q知,(xi,xj)/∈ind(P),从而存在R ∈P使(xi,xj)/∈R,即xj/∈Rs(xi),这说明R ∈P ∩rij,于是P ∩rij Ø.
充分性: 若(xi,xj)/∈Q,则xj/∈Qs(xi),此时rij={R ∈R|xj/∈Rs(xi)}.由P ∩rij Ø知存在R ∈P,使xj/∈Rs(xi),即(xi,xj)/∈R ∈P,从而(xi,xj)/∈ind(P).由(xi,xj)/∈Q的任意性知,ind(P)⊆Q.
推论3.1设R是上的知识库,Q是U上的二元关系且ind(R)⊆Q,DQ(U,R)是R相对于Q的RM-区分矩阵.则∀rij ∈DQ(U,R),有rij Ø.
证由ind(R)⊆Q及命题3.3知,∀rij ∈DQ(U,R),R ∩rij Ø,从而rij Ø.
定理3.2设R是上的知识库,Q是U上的二元关系且ind(R)⊆Q,DQ(U,R)是R相对于Q的RM-区分矩阵.若,则P是R的Q-相对约简当且仅当对P是满足∀rij ∈DQ(U,R),P ∩rij Ø这一性质的R的极小子族.
证由定义3.1及命题3.3直接验证.
下一定理表明可以利用RM-区分矩阵求有限知识库R的相对核.
定理3.3设R是上的知识库,Q是U上的二元关系且ind(R)⊆Q,DQ(U,R)=(rij)n×n是R相对于Q的RM-区分矩阵.则coreQ(R)={R ∈R|∃i,j≤n,rij={R}}.
证当|R|=1时,显然.下面设|R| >1.记S={R ∈R | ∃i,j≤n,rij={R}}.先证S ⊆coreQ(R),用反证法.设存在R ∈S使R/∈coreQ(R),则存在rij ∈DQ(U,R)使rij={R}且ind(R-{R})⊆Q.由命题3.3知(R-{R})∩rij Ø,从而存在Q0∈R-{R}使Q0∈rij,这与rij={R}矛盾.下面证明coreQ(R)⊆S.若Q1∈coreQ(R),则.由命题3.3知存在rij ∈DQ(U,R)使(R-{Q1})∩rij=Ø.从而由推论3.1得rij={Q1},于是Q1∈S.由Q1∈coreQ(R)的任意性知coreQ(R)⊆S.综上,定理得证.
§4 知识库的拓扑约简
设R是U的知识库,则(U,ind(R))是广义近似空间,记(U,ind(R))的关系诱导拓扑为Tind(R).本节给出知识库拓扑约简的定义,并探讨它与相对约简的关系.
定义4.1(1) 设R是U上的知识库,.若Tind(Q)=Tind(R)且对Q的任一非空真子集Q0,都有Tind(Q0)ind(R),则称Q为R的一个拓扑约简.R的全体拓扑约简用redT(R)表示.
(2) 设R是U上的知识库,R ∈R.当|R| >1时,若Tind(R-{R})ind(R),则称R是R的拓扑核心元素,称集{R ∈R | Tind(R-{R})ind(R)}为R的拓扑核,记作coreT(R).当|R|=1时,约定coreT(R)=R.
命题4.1若R是论域U上的一族预序,则red(R)=redT(R).
证当|R|=1时,显然.下面对|R|>1先证red(R)⊆redT(R).若Q ∈red(R),则ind(Q)=ind(R),因R是论域U上的一族预序,故ind(Q)及ind(R)是U上的预序.于是由ind(Q)=ind(R)知p(ind(Q))=p(ind(R)).从而由引理2.2知Tind(Q)=Tind(R).因Q ∈red(R),故对Q的任一非空真子集Q0,有ind(Q0)ind(R).由R是论域U上的一族预序知p(ind(Q0))(ind(R)).从而由引理2.2知Tind(Q0)ind(R).这说明Q ∈redT(R).由Q ∈red(R)的任意性知red(R)⊆redT(R).
red(R)⊇redT(R)逆推可得.综上,red(R)=redT(R).
下面定理表明知识库的拓扑约简是特殊的相对约简.
定理4.1设R是U上的知识库,R ∈R,.则
(1)Q是R的拓扑约简当且仅当Q是R的p(ind(R))-相对约简;
(2)R是R的拓扑核心元素当且仅当R是R的p(ind(R))-相对核心元素.
证下面以(1)为例证之,(2)类似可证明.
充分性: 若Q是R的拓扑约简,则Tind(Q)=Tind(R)且对Q的任一非空真子集Q0,Tind(Q0)ind(R).由引理2.2知p(ind(Q))=p(ind(R))且p(ind(Q0))(ind(R)).由命题2.1得ind(Q)⊆p(ind(R))且.这说明Q是R的p(ind(R))-相对约简.
必要性: 由引理2.2,命题2.1逆推可得.
推论4.1设R是有限集U上的知识库,Q是U上的二元关系且ind(R)⊆Q,则
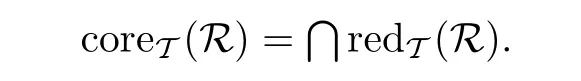
证由定理3.1,4.1直接验证.
下一命题表明,对有限知识库R中的每一成员适当扩充,不影响拓扑约简和拓扑核的构成.
命题4.2设R={R1,R2,···,Rm}是有限集U上的知识库,△={(x,x)| x ∈U}是U上的恒等关系.给定△i ⊆△(i=1,2,···,m),作R*={R1∪△1,R2∪△2,···,Rm ∪△m}.则
(1)Q*={Rj1∪△j1,Rj2∪△j2,···,Rjs ∪△js}∈redT(R*)当且仅当
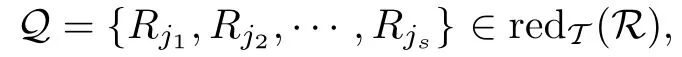
其中Rjt ∈R(t=1,2,···,s且s >1);
(2)coreT R*={Ri1∪△i1,Ri2∪△i2,···,Rik∪△ik}当且仅当coreT R={Ri1,Ri2,···,Rik},其中Rit ∈R(t=1,2,···,k且k >1).
证先证(1).必要性: 因Q*={Rj1∪△j1,Rj2∪△j2,···,Rjs ∪△js} ∈redT(R*),故Tind(Q*)=Tind(R*),从而由引理2.2知p(ind(Q*))=p(ind(R*)).因ind(Q)⊆ind(Q*)⊆△∪ind(Q),故由注2.1得,p(ind(Q))⊆p(ind(Q*))⊆p(△∪ind(Q))=p(ind(Q)).从而p(ind(Q))=p(ind(Q*)).同理有p(ind(R))=p(ind(R*)),从而p(ind(Q))=p(ind(R)).由引理2.2得Tind(Q)=Tind(R).又∀Rjt ∈Q,有Rjt ∪△jt ∈Q*.因Q* ∈redT(R*),故Tind(Q*-{Rjt∪△jt})ind(R*),从而p(Q*-{Rjt ∪△jt})(R*).由ind(Q-{Rjt})⊆ind(Q*-{Rjt ∪△jt})⊆△∪ind(Q-{Rjt})及注2.1可推得p(ind(Q*-{Rjt ∪△jt}))=p(ind(Q-{Rjt})).从而p(ind(Q-{Rjt}))(ind(R*))=p(ind(R)),进而Tind(Q-{Rjt})ind(R),这说明Q ∈redT(R).
充分性: 逆推可得.
(2)由(1)及推论4.1直接验证.
§5 知识库相对约简的求法
本节到布尔函数方面的相关知识,读者可参考文献[2]或其它相关文献.
定义5.1设R是上的知识库,Q是U上的二元关系且ind(R)⊆Q,DQ(U,R)=(rij)n×n是R相对于Q的RM-区分矩阵.称布尔函数为R的相对于Q的RM-区分函数.
定义5.2设R是上的知识库,Q是U上的二元关系且

是RM-区分函数fQ(R)的某一析取范式.若中无重复元素,且∀k,j≤m当时,Rk与Rj互不包含,则称该析取范式为fQ(R)的极小析取范式.
定理5.1设R是上的知识库,Q是U上的二元关系且ind(R)⊆Q,.若为R的相对于Q的RM-区分函数fQ(R)的极小析取范式,则P ∈redQ(R)当且仅当存在k≤m使P=Rk.
证类似于文[4]定理4.7的证明,从略.
注5.1定理5.1给出了相对约简的具体求法: 将fQ(R)化为极小析取范式则{Rk |k=1,2,···,m}恰是知识库R的全部Q-相对约简.
下面以例说明求有限知识库相对约简(包括交约简,拓扑约简)的方法.
例5.1设U={xi |1 ≤i≤8},R={Rk |1 ≤k≤5}为U上的知识库,其中
易得ind(R)={(x1,x2),(x2,x3),(x4,x5),(x5,x6)}.
下面用极小元方法求R的交约简,它们是特殊的相对约简.先由注3.2求得偏序集
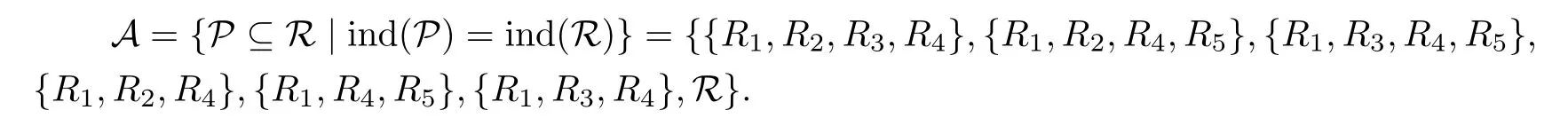
A的极小元即为R的交约简,red(R)={{R1,R2,R4},{R1,R3,R4},{R1,R4,R5}}.注意到交约简是特殊的相对约简,由定理3.1又可得core(R)={R1,R4}.
设Q={(x1,x2),(x2,x3),(x1,x3),(x4,x5),(x5,x6),(x7,x8)}是U上二元关系,则ind(R)⊆Q.下面用RM-区分矩阵和RM-区分函数求R的Q-相对约简及Q-相对核.
作R的相对于Q的RM-区分矩阵DQ(U,R)如表5.1,为了简洁,用Ri的下标i代替Ri,例如r61={2,3,5}代表r61={R2,R3,R5}.R代表{1,2,···,5}.
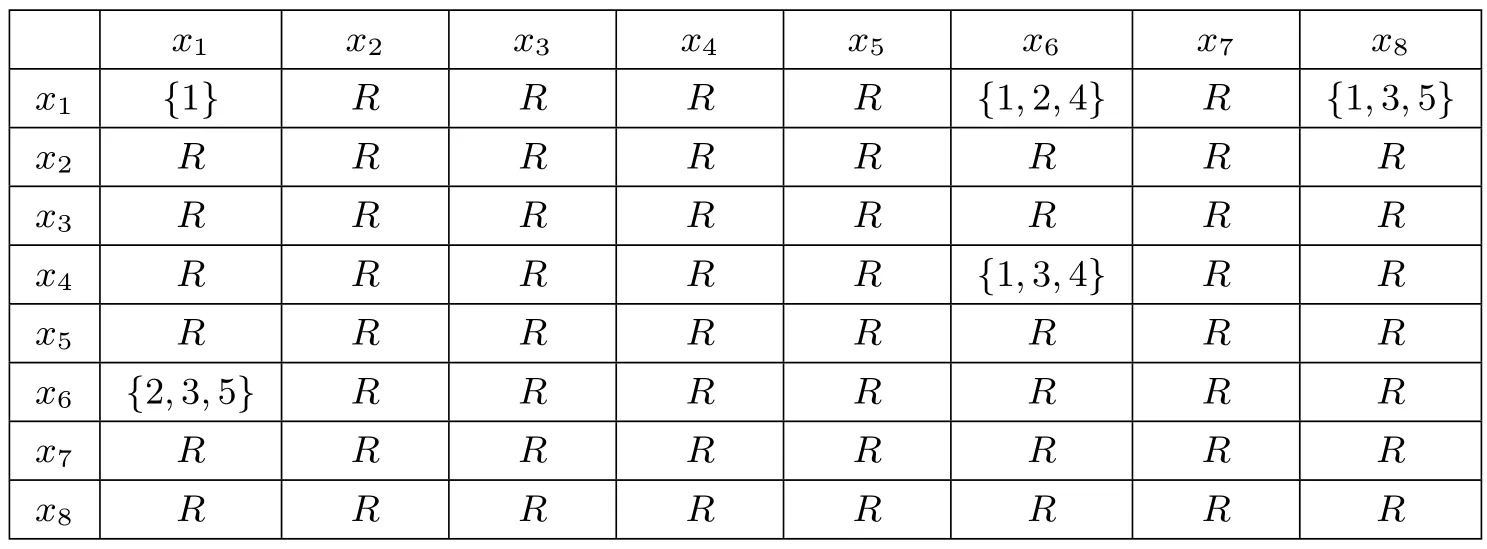
表5.1 RM-区分矩阵DQ(U,R)
将R的相对于Q的RM-区分函数化为极小析取范式
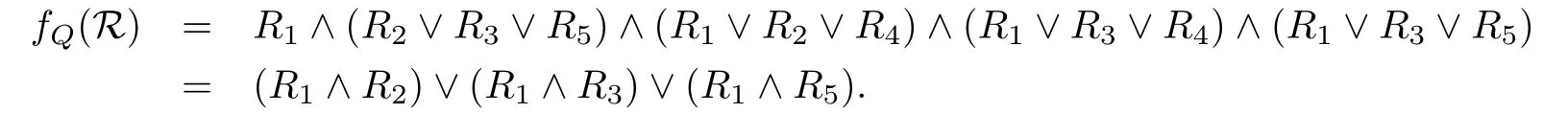
由定理5.1知R的全体Q-相对约简为redQ(R)={{R1,R2},{R1,R3},{R1,R5}};由定理3.3知R的Q-相对核为coreQ(R)={R1}.
下面用RM-区分矩阵和RM-区分函数求R的拓扑约简(特殊的相对约简)及拓扑核.
由定理4.1,先求得p(ind(R))={(x1,x2),(x1,x3),(x2,x3),(x4,x5),(x4,x6),(x5,x6)}∪△.
作R的相对于p(ind(R))的RM-区分矩阵Dp(ind(R))(U,R)如表5.2.为了简洁,用Ri的下标i代替Ri,例如r61={2,3,5}表示的是r61={R2,R3,R5}.R代表{1,2,···,5}.

表5.2 RM-区分矩阵Dp(ind(R))(U,R)
将R的相对于p(ind(R))的RM-区分函数化为极小析取范式

由定理4.1和5.1知R的拓扑约简全体为redT(R)={{R1,R2,R4},{R3,R4},{R4,R5}};由定理3.3和定理4.1知R的拓扑核为coreT(R)={R4}.
