基于PCA-IBAS-ELM的海底多相流管道内腐蚀速率预测

骆正山, 李蕾

(西安建筑科技大学管理学院， 西安 710055)

近年来中国海洋油气资源不断开发，海底管道建设持续增长，混输管道逐渐成为海底管道主流[1-2]。相比于单向流管道而言，混输管道能带来更大的经济效益，但输送介质复杂，极易引发腐蚀泄漏进而造成环境和财产损失[3]。因此，有效预测海底多相流管道内腐蚀速率具有重大现实意义。

中外学者对海底管道腐蚀开展了大量研究。在管道腐蚀机理及影响因素层面，丛军等[4]通过X射线对海底管道腐蚀产物进行了衍射分析，结果表明其管道内壁主要发生了CO2腐蚀，并对CO2腐蚀机理进行阐述，但未对其腐蚀影响因素的相关性进行深入研究；马璐等[5]通过挂片实验，电感探针，显微镜等手段对海底管道内腐蚀现状进行研究，分析了其腐蚀类型及可能存在的腐蚀因子，但未对海管内部腐蚀趋势进行预测；冯胜等[6]对海底混输管道回收管段进行实验，实验结果表明管段内腐蚀严重，以CO2腐蚀为主，同时伴随有垢下及细菌腐蚀，但未对CO2这一主要腐蚀因素进行深入分析，腐蚀影响程度有待进一步探讨；文献[7]对由CO2引发的腐蚀进行研究，但影响规律结果并不稳定，未形成定论。

在管道腐蚀预测层面，随着机器学习算法的快速发展，越来越多学者将其应用于腐蚀研究，并取得进展。靳文博等[8]利用广义回归神经网络预测了海底腐蚀管道的极限承载力，虽然得到的预测值与计算值吻合程度较好，但该网络的关键性能指标——光滑因子采用人为调试的方法确定具有局限性，且一定程度上增加了运算时间；张新生等[9]基于马尔科夫理论构建海底管道剩余寿命预测模型，但海底管道数据获取困难，马尔科夫预测又对原始数据依赖过大，导致使用受限；骆正山等[10]提出使用蝗虫算法(grasshopper optimization algorithm, GOA)优化相关向量机(relevance vector machine, RVM)对海底管道腐蚀速率进行预测，但RVM参数选择复杂，核函数要求严格，GOA收敛速度慢，因此组合使用效果不佳； Kamrunnahar等[11]使用神经网络作为数据挖掘工具对腐蚀行为进行预测，然而神经网络目标函数复杂、训练效率低，预测效果不佳。

综上所述，目前针对海底管道腐蚀问题研究，大多局限于腐蚀现象、腐蚀类型，对于腐蚀机理及腐蚀因素相关性缺少系统分析，同时现有预测所采用的机器学习算法存在弊端。基于此，现深入分析海底多相流管道内腐蚀频发的根本原因，对影响腐蚀速率的主要因素进行讨论，并提出构建PCA-IBAS-ELM组合模型，通过PCA定量筛选腐蚀因素，针对甲虫天牛须算法(beetle antennae search，BAS)存在的缺陷进行改进，改进后的IBAS算法用于优化极限学习机(ELM)关键参数，最后应用于工程实例以检验所组合模型的预测效果。

1 理论基础

1.1 腐蚀机理及影响因素

海底多相流管道介质中含有的CO2是引发腐蚀的主要原因，CO2遇水形成酸性溶液，与金属表面接触产生化学反应，生成金属盐沉积[12]。

已有研究表明，温度、pH、流体流速、压力、CO2分压和持液率等是影响腐蚀的主要因素[13]。当温度在40～60 ℃时，CO2腐蚀速率提升，钢管表面产生碳酸亚铁，出现较为严重的点蚀、坑蚀，当温度大于60 ℃时，钢管表面易形成保护膜[14]，从而减缓腐蚀，在60～70 ℃时，腐蚀达到峰值；酸性条件下，产生的H+加剧阳极反应，腐蚀加速；管道内腐蚀速率随流体流速的增加而提升，流体流速增加导致管道承受的切向力加大，切向力会破坏管道表面形成的保护膜，从而加快腐蚀；压力对腐蚀速率的影响也较为明显，压力增大时，管道内腐蚀表面受到的应力加大，同时伴随化学腐蚀产生，腐蚀加速；CO2分压对腐蚀速率的影响与温度有关，当温度在60 ℃以下时，随CO2分压加大腐蚀加快，当温度在60 ℃以上时，随CO2分压加大，管道内表面将形成腐蚀产物膜，阻碍腐蚀发生；在多相流管道中，持液率越大，越容易在管道表面形成水膜，酸性气体溶解其中，生成酸性介质，从而加速腐蚀,持液率越小，管道表面越干燥，腐蚀不易发生。

1.2 算法原理

(1)主成分分析法。主成分分析(PCA)[15-17]算法是通过对原始数据集进行一系列矩阵变换，在信息损失最小的前提下实现降维。其重点是求解协方差矩阵的特征值及特征向量，根据特征值对主、次位置进行排序，提取位置靠前的因子作为主因子。算法详解参见文献[18]。

(2)极限学习机。极限学习机(ELM)[19-20]是一种简单易用且高效的单隐层前馈神经网络。该方法的输入权值w和隐层阈值b随机设置，输出权值 通过公式计算得到，在预测过程中只需要调整隐层神经元节点的数量，选择适当的传递函数。ELM具有学习速度快，泛化性能好等优点。算法详解参见文献[21]。

(3)甲虫天牛须算法。甲虫天牛须算法(BAS)是一种生物启发式智能优化算法，其过程是对甲虫觅食行为的模拟[22-23]。甲虫通过左右两须对气味强弱进行判断，决定行进方向，逐步接近食物所在位置。BAS具有结构简单、初始参数少、收敛速度快等优点。算法详解参见文献[24]。

2 甲虫天牛须优化算法改进

2.1 拓展种群改进

原始甲虫天牛须算法(BAS)是单个个体的寻优过程，在面对复杂问题时寻优能力有限，故将其拓展为种群活动。将k维空间中的天牛群按比例分为搜索者，追随者和探索者。搜索者搜寻最优解，追随者在其周围寻找潜在解，探索者全局活动，三者协作可有效避免系统陷入局部最优。改进后的甲虫群朝向和左、右须位置定义同BAS为

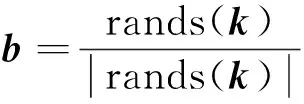
(1)

式(1)中：b为甲虫朝向；rands为随机函数；k为空间维度。

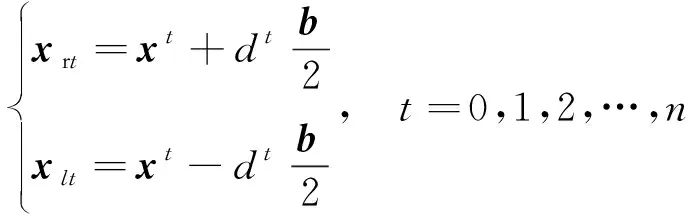
(2)

式(2)中：xrt为天牛右须第t次迭代时的位置坐标；xlt为天牛左须第t次迭代时的位置坐标；xt为天牛第t次迭代时的质心坐标；dt为天牛第t次迭代时两须之间的距离，有dt+1=dt×0.95。

迭代过程由单一甲虫特定移动方式改进为三个子群体遵循不同轨迹协作进行。搜索者以式(3)更新位置，即

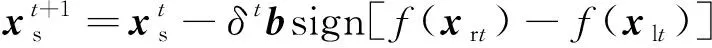
(3)

追随者在当前最优解周围小范围移动，寻找潜在解，以式(4)更新位置，即

(4)

探索者以固定的步长随机移动，以式(5)更新位置，即

(5)

2.2 自适应步长改进

甲虫行进过程步长迭代的关键是步长因子，决定了收敛速度的快慢。原始天牛须算法的步长因子为固定值(0.95)，为了获得更好的优化能力，提出了一种改进动态步长因子的方法。在优化初始阶段，为了扩大搜寻范围，加快寻优速度，采用较大步长因子；在优化的后期，搜索趋于稳定，为了提高解的精度，减小了步进因子。基于以上考虑，作出如下调整。

(6)

3 模型构建

3.1 PCA-IBAS-ELM模型构建

首先，将腐蚀因素通过主成分分析降维得到主要因素，过程如下。

(1)消除因素之间量纲影响，按式(7)作归一化处理，即

(7)

(2)归一化数据构成矩阵X，矩阵X的协方差矩阵R计算公式为

(8)

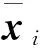
(3)最后计算R的特征值及特征向量，并按式(9)计算贡献率，按式(10)计算累计贡献率，累计贡献率85%以上的因素定为主因素，分为训练集及测试集。

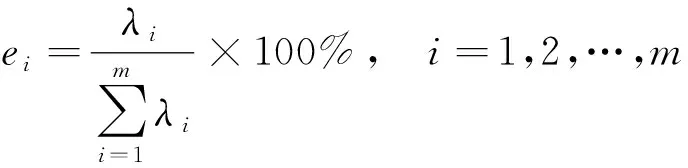
(9)

式(9)中：ei为单个因素的贡献率；λi为R的特征值。

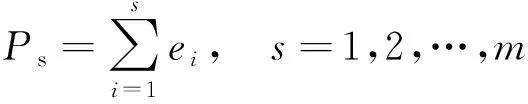
(10)

式(10)中：Ps为各因素累计贡献率。

其次，将训练集代入IBAS搜寻最优权值阈值，过程如下。

(1)初始参数设定。选取10个个体组成的天牛群，初始步长δ0为10，最小步长δmin为0.01，两须初始距离d0为0.05。

(2)种群位置初始化，比较适应度值大小。随机初始化甲虫位置，在初始位置对搜索者左右两须适应度值进行比较,综合判别最佳行进方向，以式(3)移动，追随者、探索者遵循2.1节所讲方式协助寻优。

(3)步长更新。迭代完成，将当前最优适应度函数值和历史最优进行比对，根据比较结果按式(6)更新步长因子。

(4)当适应度值达到预设精度或迭代次数达到上限，终止运算，输出最优解。

最后，将优化后的wj、bj代入ELM，模型目标转为按式(11)计算输出权值β，进而得到预测值。

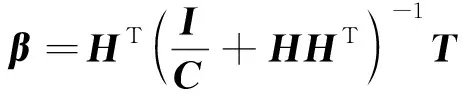
(11)

式(11)中：C为惩罚参数；H为隐含层输出矩阵；HT为H的转置；T为输出矩阵；I为单位矩阵。

在得到输出权值β后，预测值可表示为

(12)

式(12)中：xi为输入参数；yi为输出参数；wj为输入权值；bj为隐含层神经元阈值；g(x)为激励函数；L为隐含层节点数；N为任意样本数。

3.2 模型验证指标

选取以下三项指标评价模型性能，即平均绝对误差(MAE)、平均绝对百分误差(MAPE)及均方根误差(RMSE)，与平均误差相比，平均绝对误差更能反映预测值误差的真实情况，均方根误差可反映出预测的稳定性。计算公式为

(13)

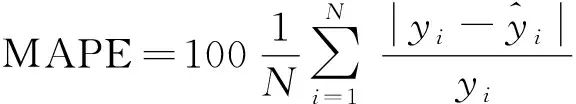
(14)

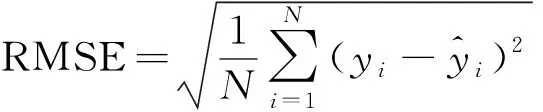
(15)

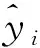
4 实证分析

4.1 数据准备

本文数据来自中国海南东部的某海底油气管道，选取其中50个位置点的腐蚀影响因素及腐蚀速率进行研究，如表1所示。

表1 内腐蚀速率及影响因素数据Table 1 Internal corrosion rate and influencing factors data

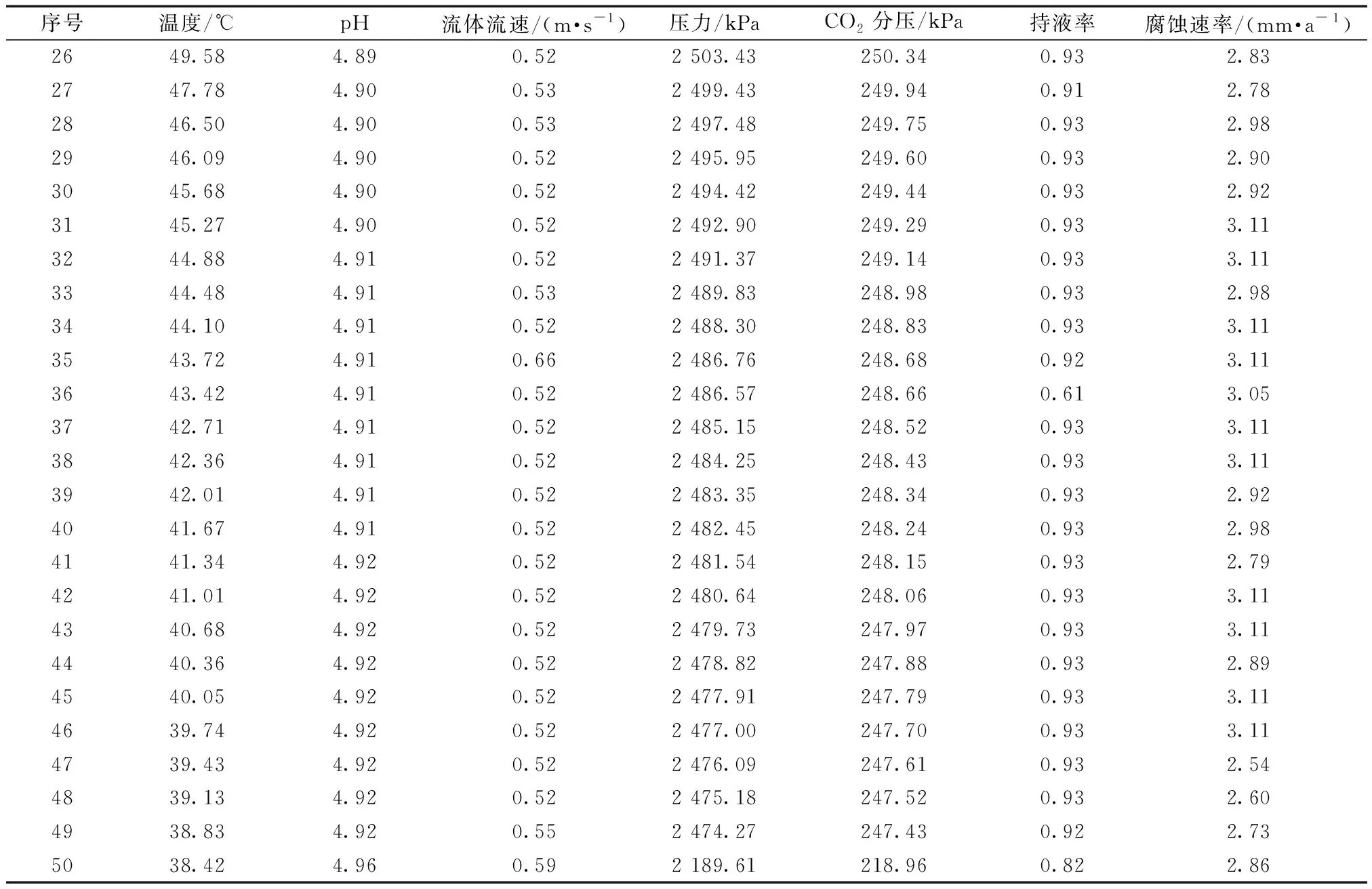
续表1

4.2 PCA因素提取

根据PCA算法原理，通过MATLAB软件，得到上述因素的贡献率ei及累计贡献率Ps，如表2所示。

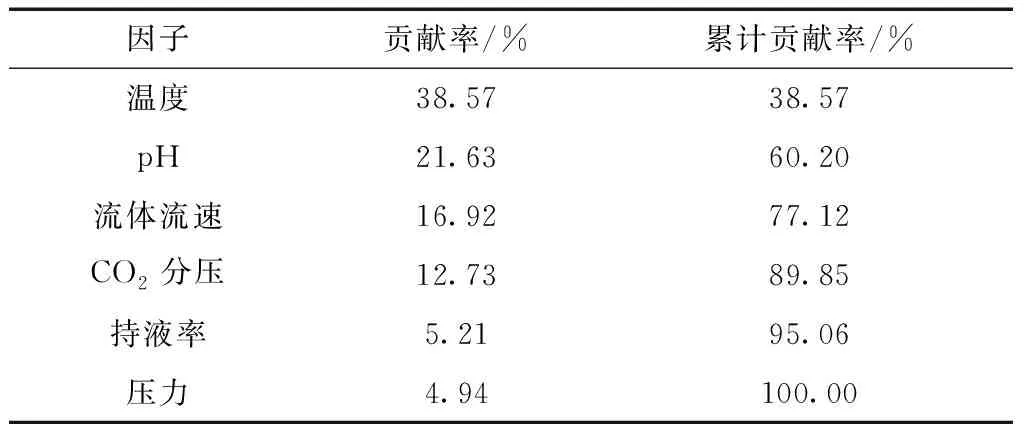
表2 PCA算法处理结果Table 2 PCA processing results

由表2可知，温度对多相流海底管道内腐蚀的影响较大，贡献率达到38.57%，压力对其影响较小，贡献率仅为4.94%。选取累计贡献率85%以上的因素为主要因素展开下一步研究，即温度、pH、流体流速和CO2分压。

4.3 模型训练

将PCA筛选后的数据代入IBAS-ELM模型进行训练，其中40组为训练集，10组为测试集。甲虫种群中的30%、60%、10%分别设为搜索者、追随者和探索者，最大迭代次数为200，适应度函数如式(16)所示，模型激活函数为Sigmoid函数如式(17)所示。

(16)

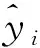
(17)

迭代过程如图1所示，由图1可见IBAS算法寻优效果良好，在45次迭代之后趋于稳定，此时适应度函数值为0.033 47。

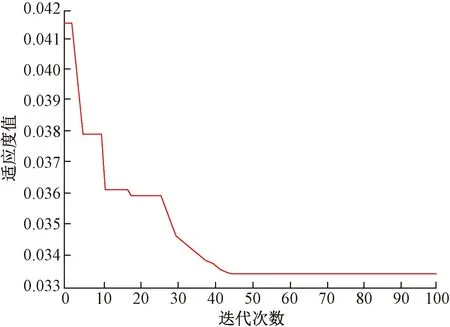
图1 IBAS-ELM迭代过程Fig.1 IBAS-ELM iterative process

4.4 模型结果对比

将测试数据集代入IBAS-ELM模型中，得到预测值，选用BAS-ELM和ELM两个模型与之对比，结果如图2所示。分析可知，PCA-IBAS-ELM的预测值与真实值差距较小，拟合效果更佳。

为检验模型预测精度，采用相对误差作为评判标准，对比结果如图3和表3所示。

图2 预测结果对比图Fig.2 Comparison of prediction results

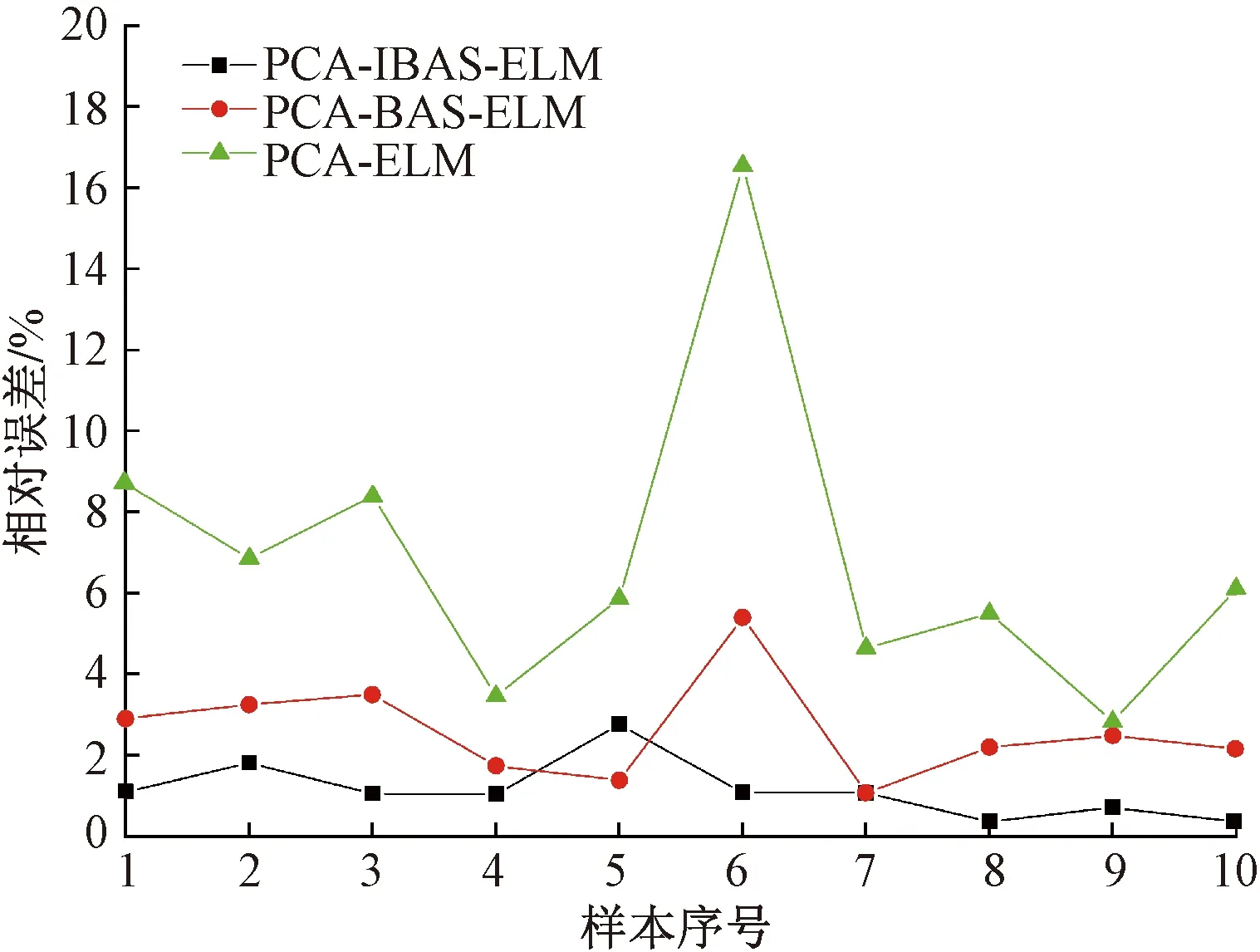
图3 相对误差对比图Fig.3 Comparison of relative errors

结合图3和表3分析可知， PCA-IBAS-ELM除第5组数据外其余误差均小于其他两种模型，其相对误差的平均值为1.132%，低于PCA-BAS-ELM的2.604%和PCA-ELM的6.887%。为进一步评价模型性能，采用3.2节中的指标对以上3种模型再次对比，结果如表4所示。

由表4可知，PCA-IBAS-ELM模型的MAE、MPAE、RMSE均小于其他两种模型，三种模型的预测精度从高到低分别为PCA-IBAS-ELM、PCA-BAS-ELM、PCA-ELM，说明采用算法对ELM的输入权值和隐层阈值进行优化可提升预测效果，同时IBAS的优化性能高于BAS。

5 结论

提出了以PCA-IBAS-ELM组合模型对海底多相流管道内腐蚀速率进行预测，在分析腐蚀机理，介绍模型算法的基础上，结合中国海南东部某海底油气管道的50组数据实际验证，得出以下结论。

(1)PCA提取出保留原有样本信息89.85%的4个关键因素，作为ELM的输入指标，消除了叠加信息的影响，减小了计算压力，同时采用IBAS对ELM的输入权值及隐藏层阈值进行优化，克服了其随机设定带来的不稳定性，提高了预测精度。

(2)将PCA-IBAS-ELM与PCA-BAS-ELM进行对比，均方根误差(RMSE)、平均绝对误差(MAE)及平均绝对百分误差(MAPE)分别减小了0.043、0.041、1.513%，表明将单个甲虫的寻优拓展为种群协作，同时将固定步长因子做自适应改进提升了优化算法的性能。

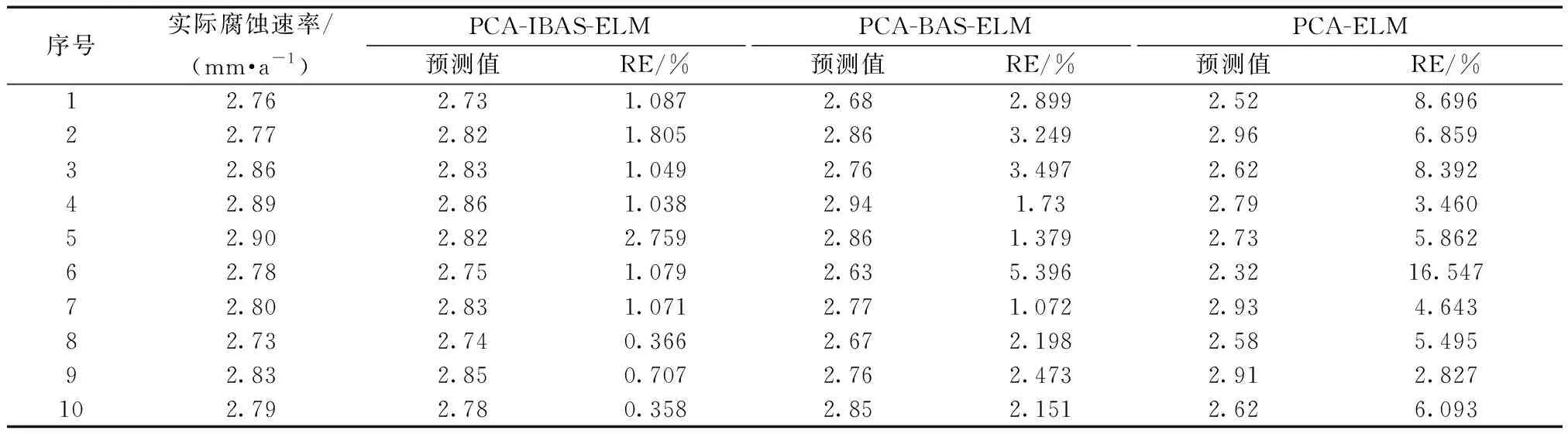
表3 预测相对误差结果分析Table 3 Analysis of relative error results

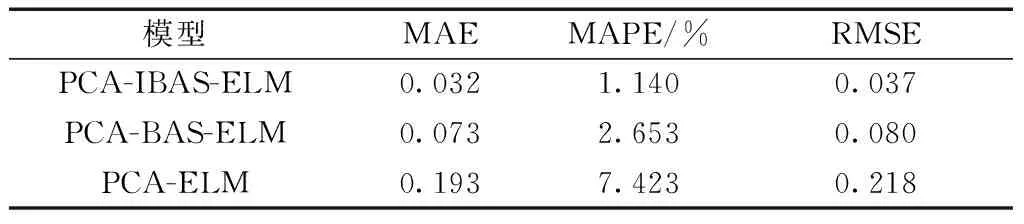
表4 模型预测结果性能指标值Table 4 Performance index values of the prediction results