当地DFD方法向LES湍流模拟推广的研究

徐振东，段宇轩，徐华松，杨 帆，李 铁

（上海机电工程研究所，上海 201109）

0 引 言

流体数值模拟中涉及到复杂区域，需要生成贴合物面边界的曲线网格，即贴体方法，通过变换坐标系来构造贴体网格，由于其近壁处理的准确性已被广泛使用。然而，为复杂结构生成贴体网格可能非常耗时。模拟动边界流动时所需的瞬态网格重新划分进一步增加了计算成本和算法复杂性。浸没边界法能够简化网格生成。此外，当使用IB 方法时，高效的笛卡尔求解器可以直接应用于复杂问题。

Peskin开创的IB方法最初用于研究心血管循环中的流固耦合相互作用。到目前为止，为了提高该方法的稳定性和适用性，众多学者已经提出了许多修正。在Iaccarino和Verzicco以及Mittal和Iaccarino的文章中可以找到对不同技术的详细讨论。尽管IB方法在模拟层流方面取得了非凡的成功，但其在湍流中的应用并不广泛。大涡模拟（LES）是一种经济有效的湍流模拟方法，其对控制方程进行空间过滤以解决大尺度的动力学问题，并且仅对“通用”小尺度进行建模。与LES 相比，雷诺平均NS 方程（Reynoldsaveraged Navier-Stokes equations，RANS）模拟无法正确捕捉由湍流各向异性引起的二次流，直接数值模拟（direct numerical simulation，DNS）对于工程中的复杂湍流计算密集且不切实际。随着雷诺数（）的增加，需要对近壁流进行高分辨率模拟。IB 方法的一个主要限制是笛卡尔网格无法将节点聚集到实体边界，即使进行了网格局部细化，用于模拟湍流的笛卡尔网格的节点总数仍然非常大，对于三维流动这种情况尤其突出。在LES 环境中，必须明确求解近壁区域中最具能量的流动结构，并且网格分辨率与DNS的分辨率相当。这使得在IB 方法中进行中高雷诺数的LES 是不可行的。克服这一困难的一种方法是使用壁面模型求解近壁面流动，该模型通常以壁面剪应力的形式为外部LES 提供近似边界条件。因此，在壁面模化的LES 中，网格间隔尺度与黏性壁单元无关，而是与边界层厚度有关。

Shu等提出了一种IB方法，称为自由域离散化（DFD）方法，用于求解不规则域上的偏微分方程（partial differential equation，PDE）。在DFD 方法中，在IB 紧邻的内部节点处的偏微分方程的离散形式可能涉及一些外部节点，这些外部节点起到实现边界条件的作用。在DFD方法的早期应用中，外部相关节点处的函数值沿仅涉及两个边界点的整个网格线进行评估，这种方式不适用于复杂的领域。为了使该方法更通用，开发了一种当地DFD 方法，外部相关节点处的数值通过沿垂直于壁的方向结合边界条件进行适当的局部外推，在每个时间步进行更新。

在当地DFD 方法中，应在壁法线上和解域内构造一些点，这些参考点通常不是网格节点，也被称为虚拟点。虚拟点离壁面的距离约为一个局部网格间隔。到目前为止，当地DFD方法已成功应用于模拟各种无黏性或层流。Zhou通过引入壁面模化技术将该方法扩展到高雷诺数湍流的RANS 模拟，以减轻对湍流边界层的网格分辨率的要求。

本文在LES 框架中实现了当地DFD 方法，动态亚网格尺度（SGS）模型用于湍流闭合，并且将由Meneveau 等提出的拉格朗日平均法应用于SGS 模型系数的动态计算。为了减少靠近壁面区域的网格间隔，引入了基于湍流边界层方程（turbulent boundary-layer equations，TBLEs）的壁面模型。

本文详细讨论了外部相关节点处的流量变量的处理，并进行数值实验以验证当前LES-DFD 方法的能力。

1 数值近似的控制方程和基本方案

本文考虑等密度和等黏性系数的紊流。过滤形式的连续性方程和动量方程表达为

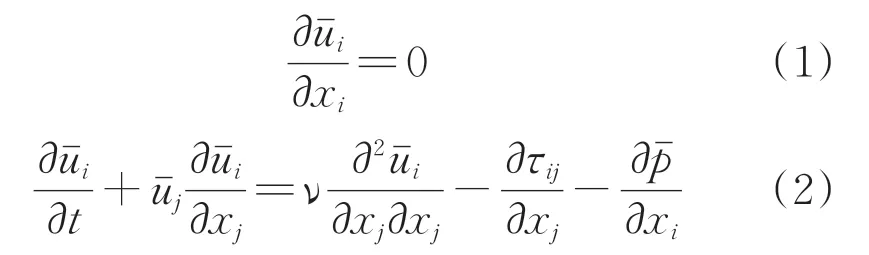
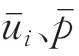
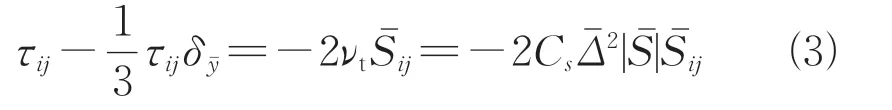
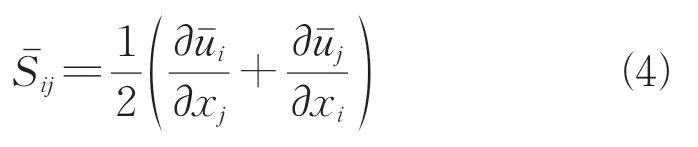
对于本文中使用的四面体网格，过滤尺度与网格间距相关，通过单元体积的立方根计算。为了确定系数C，引入了Meveneau等提出的拉格朗日平均法。

1.1 控制方程的空间近似

使用式（3）对τ的定义，控制方程（1）和（2）可以改写为以下无量纲形式：

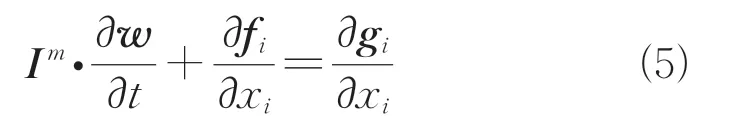
式中：、f、g分别是流动变量、对流通量和黏性通量矢量；I是修正单位矩阵。

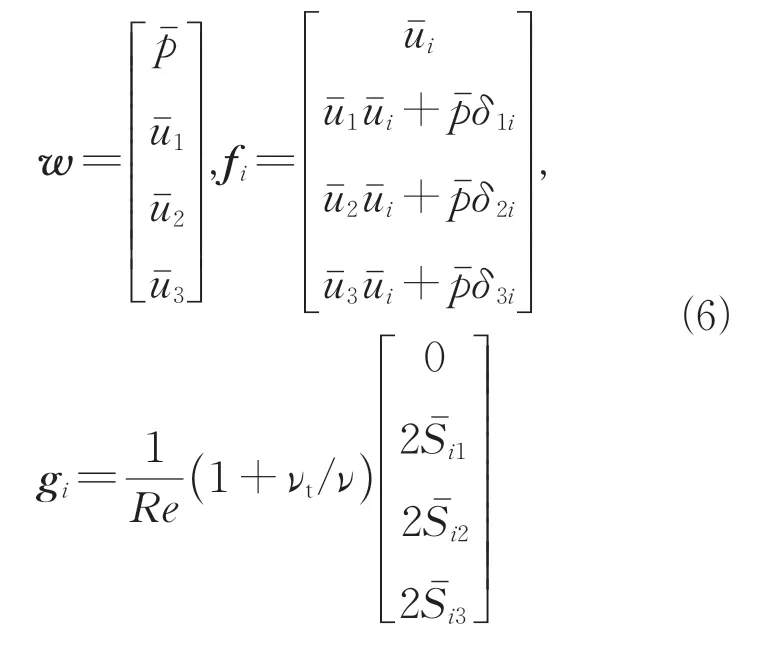
式（6）中：为无量纲层流黏性系数；=/为雷诺数，为特征速度，为特征长度。

I是修正单位矩阵，从连续性方程中消除压强的时间导数

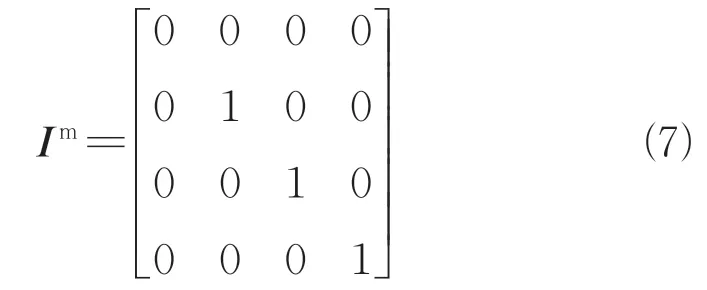
假设⊂R是一个包含一个实体的连通开集，由四面体网格离散化。将Mavriplis和Belov提出的Galerkin有限元方法应用于可压缩Navier-Stokes方程和集总质量矩阵的概念，可以得到节点处控制方程（5）的半离散形式为

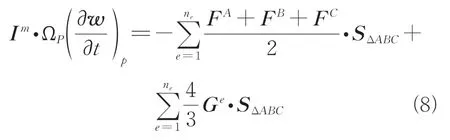
式中：表示非黏性通量张量；表示黏性通量张量；n是共享顶点的所有四面体的数量；Ω是这些四面体的体积总和。如图1所示，表示与相对的三角形面的有向（向外法线）面积。F、F和F是三个顶点处的非黏性通量张量，G是每个四面体上的恒定黏性通量。

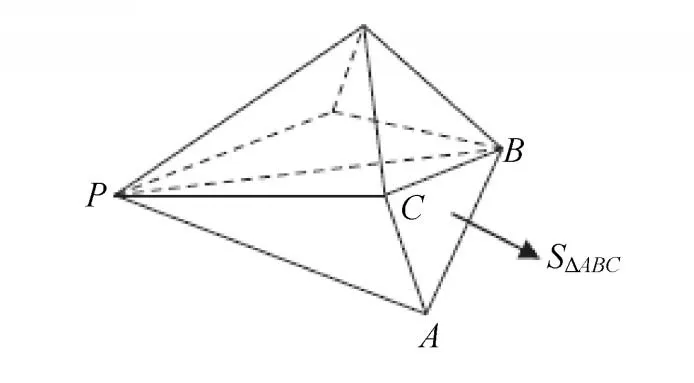
图1 四面体影响域边界面的有向面积Fig.1 Directed area of influence-domain-boundaryface of a tetrahedron

1.2 时间离散化

双时间步长用于控制方程的时间离散化。

空间离散化将式（5）变换为式（9）所示的耦合常微分方程组。

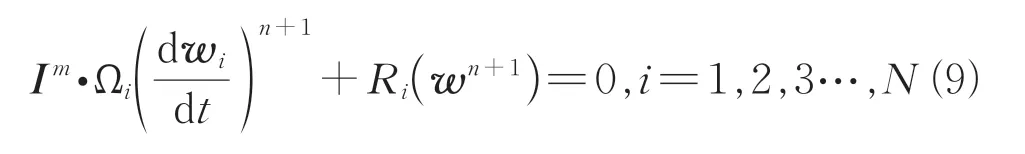
式中：是计算节点的总数；是时间步长序号；R()是离散对流通量()和黏性通量()的总和。

将关于虚拟时间的推导添加到式（9）中，得到

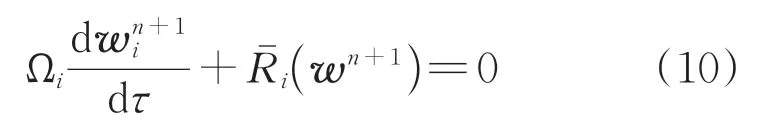
在每个物理时间步，式（10）的解是通过在虚拟时间内进入稳态而得到。

根据Belov 等的工作，在残差R()中添加了人工可压缩性项，以减少声波和对流波的差异。引入当地预处理矩阵，可产生

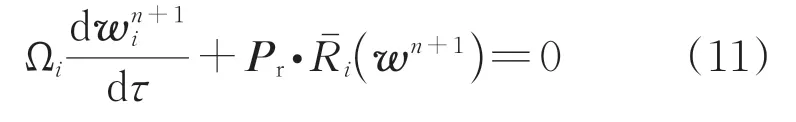
2 IB方法

根据第1.1 节中描述的空间离散化，任何网格节点的解都取决于通过四面体的边与该节点相连的相邻节点的解。对于与固体边界相交的单元边缘，内部节点（位于流体域中）的流动变量通过求解控制方程来计算，边的另一端是该内部节点的外部相关点。如图2所示，节点是内部点、和的外部相关点。为了使控制方程的离散形式封闭，外部相关点（点）上的流动变量值通过边界附近解的近似形式进行重构。解的近似形式的构建通过沿着物面法向的外插实现，插值过程中嵌入边界条件，这是当地DFD 方法的基本思想。

为了求解外部相关点上的流动变量，需要构造一个虚拟点。虚拟点在三个维度上的定义描述如图2所示。对于外部相关点，首先计算法线与壁面的交点，以及法线与顶点都是内部节点的离墙最近的三角形面的交点。和之间的距离用δ表示，然后可以得到一个常数=maxδ，其中N是外部相关点的总数。法线上的点与主体截距点的距离为，被定义为外部相关节点的虚拟点。处的流量变量可以通过其主四面体上的线性插值获得（图2中的）。

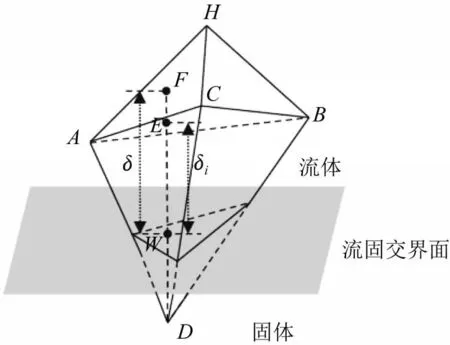
图2 浸没边界模型Fig.2 Immersed boundary model

2.1 层流外部相关点处流动变量的计算

在层流的当地DFD 方法中，外部相关点（图2中的）处的笛卡尔速度分量通过使用虚拟点处的确定值并施加无滑移边界条件确定。为了考虑体加速度的影响，在计算节点处的压强时，考虑了以下垂直于壁面方向的简化无黏动量方程：

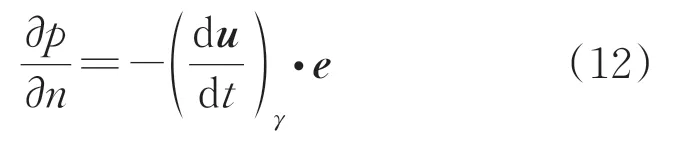
式中：是流体的速度矢量；是垂直于壁面的单位外向矢量。使用无穿透条件，可以得到处的压强为

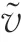
2.2 湍流外部相关节点处过滤流动变量的评估

在这项工作中，引入了一种基于简化TBLEs的壁模型，其中仅保留扩散项，即Tessicini 等提出的平衡应力模型，用于为LES 提供近似壁边界条件。在确定外部相关节点处的速度分量时，不采用无滑移条件，而是采用无穿透条件和壁模型产生的壁剪应力。本文采用平衡壁面模型。

根据壁面截点处无穿透的条件，线性外推法给出处的法向速度

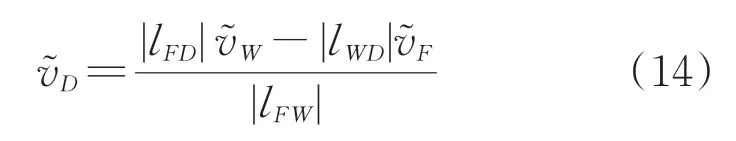
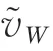
如果网格足够细，则可以使用无滑移边界条件和线性外推计算处的切向速度，如图3（a）所示。为了降低对近壁面网格分辨率的要求，采用壁面建模技术，并通过规定的壁面剪应力计算处的切向速度。如图3（b）所示，壁面模型将无滑移边界条件转化为了滑移边界条件（点的切向速度非零）。

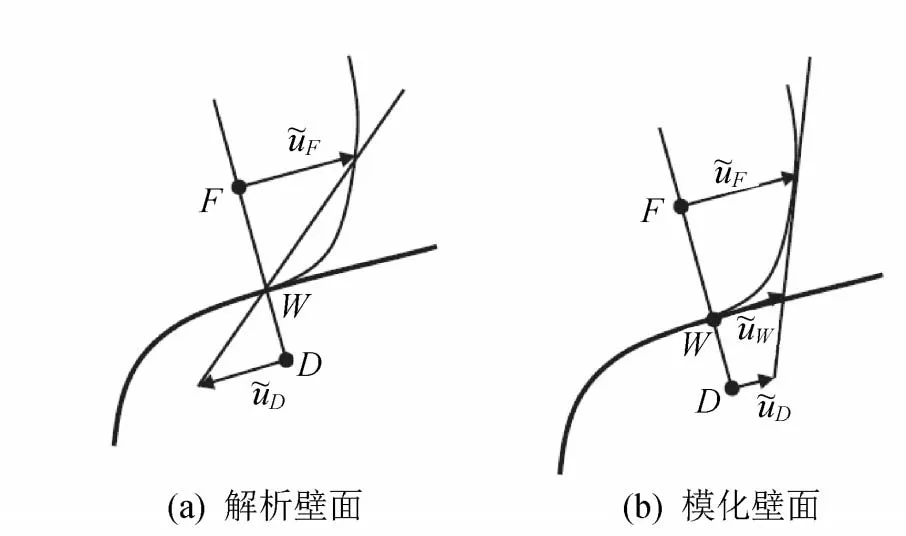
图3 浸没边界的壁面模型Fig.3 Wall modeling for immersed boundary

壁面剪应力τ可以近似为

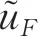
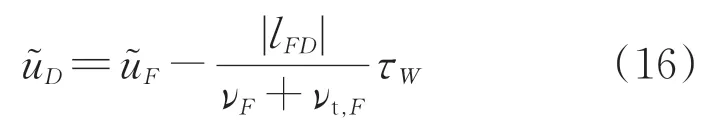
式（16）中的τ是通过壁面模化技术计算的，采用的壁面模型是基于湍流边界层方程假设的。

在已知法向和切向分量的情况下，可以直接获得外部相关节点处速度的笛卡尔分量。利用式（13）计算压强。最后，在IB附近的一个节点处的离散形式是封闭的。

3 数值试验

后台阶流动的几何外形简单，但是包含分离、再附着、分离泡等复杂流动现象，适用于LES 方法的可靠性验证。

图4为后台阶的几何机构和计算域的示意图，计算域的流向、横向、展向尺寸分别为：L/=40、L/=6、L/=3，扩张比为L/(L-)=1.2，台阶前方的长度为L/=40。雷诺数=/为5 000。入口条件为速度条件，速度型取Spalart获得的平板湍流边界层速度型；出口条件为对流边界条件，即=L面上的Cartesian速度分量u满足

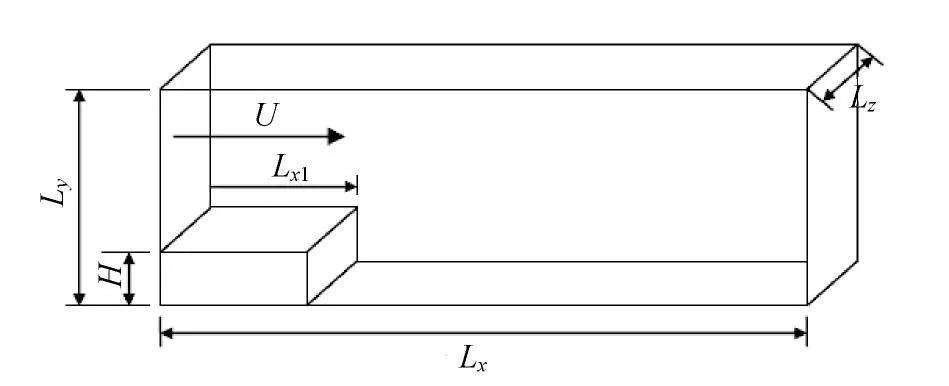
图4 后台阶流动的计算域示意图Fig.4 Flow over back step

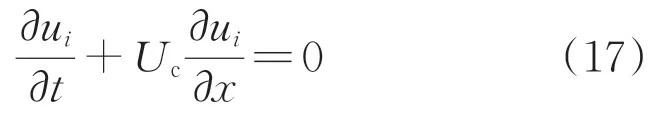
式中：为出口的平均流向速度。

计算域的上边界采用对称边界条件；展向采用周期性边界条件；下壁面上的无滑移边界条件利用非平衡解析壁面模型转化为无穿透边界条件和壁面切应力条件，边界网格与后台阶物面不重合。

图5分别为采用平衡型壁面模型和无壁面模型计算得到的平均流场的流线。Le等的DNS 结果显示在台阶拐角处存在一个二次分离泡，无壁面模型计算得到的二次分离泡的大小与DNS 结果相差较大。

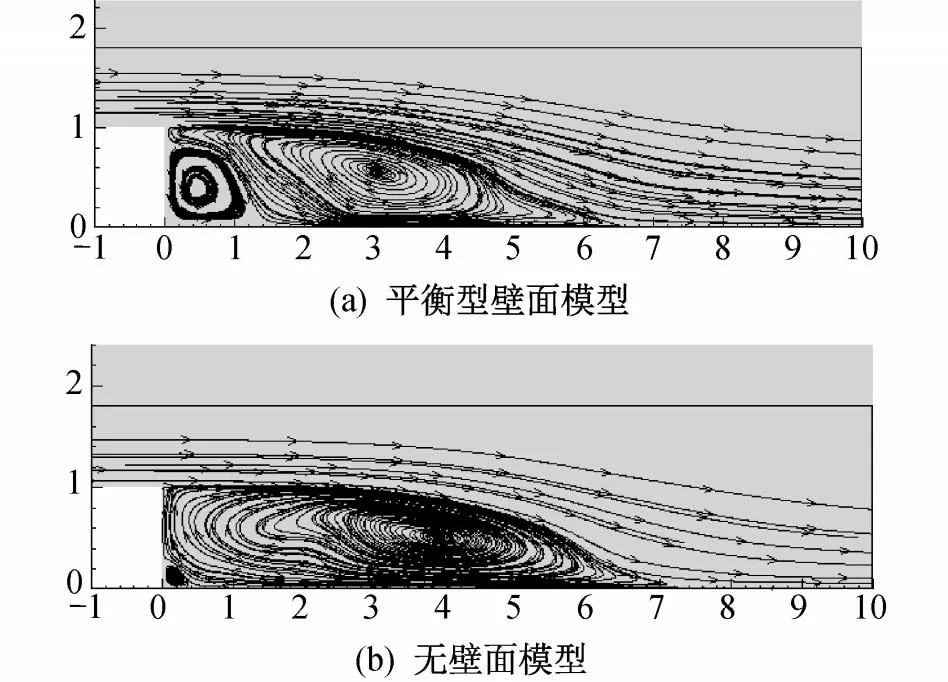
图5 平均流场的流线Fig.5 The streamlines of the mean flow field

图6为流向位置/=0.5 和/=1 处的时间平均流向速度分布，并与DNS 结果进行对比。图中红色实线表示采用壁面模型的计算结果，绿色虚线表示不采用壁面模型的计算结果，黑色虚线表示DNS 的计算结果。由于不采用壁面模型得到的二次分离泡明显偏小，因此不采用壁面模型得到的速度型在壁面附近与DNS 结果偏差较大，而采用了壁面模型得到的速度型与DNS 结果更接近。

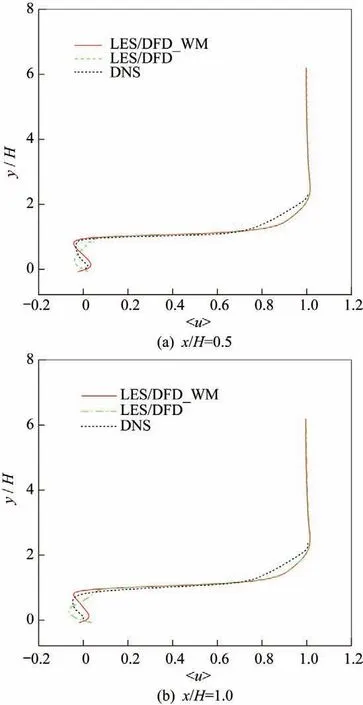
图6 时间平均流向速度Fig.6 Mean flow velocities

图7为采用平衡壁面模型计算得到的雷诺应力（、、），并与无壁面模型和Jovic、Driver 的实验结果进行对比。图中红色实线表示采用平衡壁面模型得到的计算结果，蓝色虚线表示采用无壁面模型得到的计算结果，方形符号表示实验结果。可以看出，平衡壁面模型的计算结果与参考的实验结果吻合良好，无壁面模型的计算结果在近壁面与试验结果误差相对更大，该算例的计算结果一定程度上说明了LES-DFD 方法与平衡壁面模型结合的可靠性。

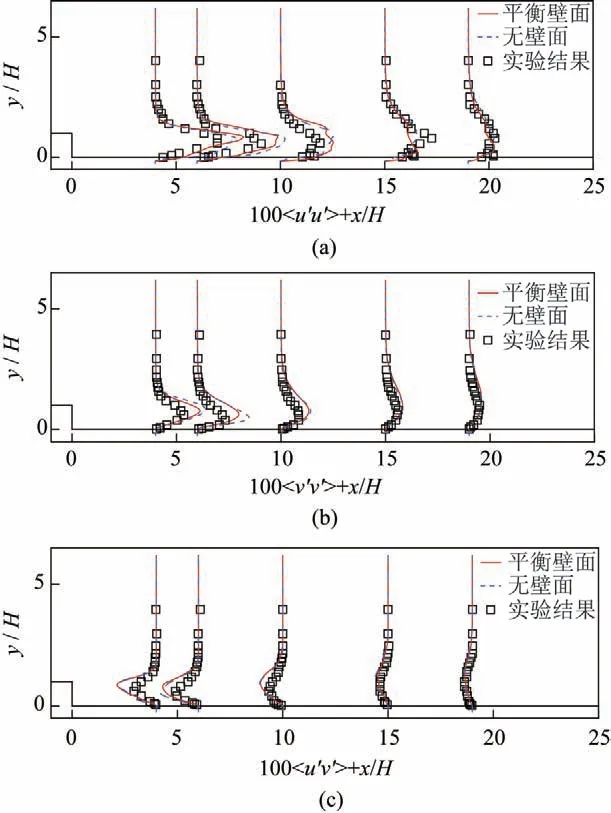
图7 不同流向位置处的雷诺应力Fig.7 Reynolds stress at different flow directions

4 结束语

本文将当地DFD 方法推广应用于湍流LES 模拟。采用基于简化的湍流边界层方程的壁面模型对浸没边界进行处理，将无滑移边界条件转化为无穿透边界条件和壁面剪切应力，以计算外部相关节点上的速度分量。

通过数值试验将后台阶流动的平均流向速度和雷诺应力与已发表的实验数据和数值结果进行了比较。结果表明，将壁面模型引入DFD方法可以有效地降低近壁面网格分辨率的要求，大大降低了计算成本。采用壁面模型得到的计算结果比采用无壁面模型得到的计算结果更接近参考结果，验证了引入壁面模型的可靠性和高效性。