高马赫数钝头体气动/传热一体化计算方法研究
2022-09-29吴王浩徐振东
吴王浩,段 旭,张 鑫,陈 丹,徐振东
(上海机电工程研究所,上海 201109)
0 引 言
随着飞行器飞行速度的不断提高,高马赫数下的气动加热逐渐成为一个不得不考虑的问题。在高马赫数绕流的边界层内,空气的大部分动能都会向内能转化,从而产生气动加热效应,导致飞行器表面的空气温度非常高。空气在极端的高温条件下会发生化学反应,随着温度的进一步升高,还会发生离解甚至电离。长时间的气动加热会使结构内部温度发生变化,引起温度分布不均匀,从而会产生结构的变形,甚至发生断裂。
对于一些简单外形,一般是在其表面铺设烧蚀材料来进行防热处理,这种方法简单而且有较高的裕度,对于气动热预测的精度要求不高。随着飞行器外形变得越来越复杂,飞行环境越来越苛刻,对飞行器热防护提出的要求也越来越高。尤其是近几年高马赫数飞行器的不断发展进步,和以前的再入飞行器不同,现在的高马赫数飞行器设计要满足长时间的临近空间飞行,可重复使用等要求,这就导致热防护技术面临新的问题,长时间的飞行所产生的热累积效应非常严重,所以对气动加热的预测精度有了更高的要求。
根据经验,在高马赫数飞行状态下,一般飞行器受气动加热最严重的位置往往位于前缘驻点处,所以驻点处气动加热效应需要着重关注。受限于计算能力,早期对于飞行器整体热流求解困难,一般使用经验或者半经验的工程估算方法计算驻点处加热状况。
传统方法将气动加热与结构传热分两步进行计算,不考虑结构温度变化对流场的影响。使用气动-传热耦合计算考虑了结构传热与气动加热之间的相互作用,更接近实际情况。为了准确地预测气动加热对飞行器结构所产生的影响,需要考虑气动加热和结构传热耦合分析。
对于高马赫数钝头体的气动加热问题,Wieting等进行了实验和仿真计算;Dechaumphai等研究了气动、传热和结构应力的耦合计算;黄唐等完成了二维的流场、热、结构一体化数值模拟;张智超等对高马赫数气动热数值计算中壁面网格划分尺度进行了讨论;夏刚等对迭代耦合和单向耦合求解结构传热进行了对比。
本文求解高马赫数钝头体流场,验证了流场求解和高马赫数下热边界确定的准确性;使用迭代耦合实现了气动-传热的一体化计算;同时对比了迭代耦合计算和单向求解计算得到的结果之间的差异。
1 计算方法
1.1 流动控制方程
使用CFD 数值求解方法进行高马赫数飞行状态下的气动加热模拟,使用的基本方程为N-S方程,积分形式的N-S方程如下:
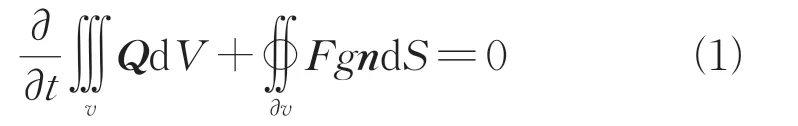
式中:=(,,,,)为守恒向量;、(,,)和分别是密度、直角坐标系下的速度分量和单位质量气体的总能量;∂是某一固定区域的边界;是边界的外法向量;矢通量可分解成对流矢通量和粘性矢通量两部分。
对于完全气体,其状态方程为

式中:为空气压强;为气体密度;为气体常数;为气体温度;为气体焓值;为气体定压比热。
1.2 热传导方程
热传导是由于温度梯度导致的能量转移而产生的。直角坐标系下,基于各向同性假设的二维瞬态热传导方程可以写成以下形式:
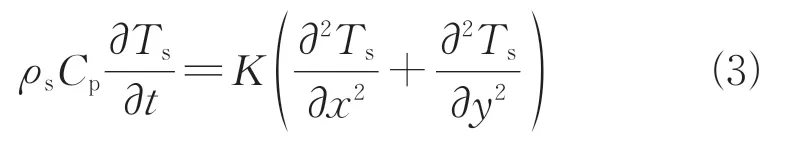
式中:为固体密度;为固体的定压比热;为固体温度;为固体的热传导系数。
本文由于结构温度变化不大,温度变化对热传导系数的影响很小,所以不考虑温度变化对材料特性所产生的影响。
1.3 耦合计算方法
通过迭代耦合的方法实现了气动-传热的耦合计算。图1为迭代耦合数据传递示意图,其中:为瞬时表面热流分布;为瞬时表面温度分布。在流场和结构传热的瞬态计算的每个时间步上,由于时间步长很小,所以对于流场来说可以认为每个时间步上结构表面的温度是不变的,对于结构传热来说可以认为每个时间步上的热流边界也是固定不变的。
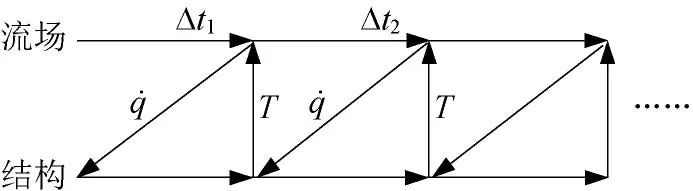
图1 迭代耦合数据传递示意图Fig.1 Data transfer of iterative coupling method
迭代耦合的步骤如下:
1)假定物体初始时刻结构温度是一个固定值,在计算流场时将物体表面看作等温壁,求解稳态流场得到一个结构表面的初始热流边界。
2)将流场与结构的交界面作为耦合边界,在边界上进行流场与结构之间数据的传递,进行非定常的模拟。
3)在时间步Δt中,假定结构温度不变,可以求得该时间步上流场的结构表面热流。
4)将流场求得的热流传递到结构传热瞬态计算中作为该时间步的热流边界,假定热流边界在该时间步内固定不变,进行传热计算,得到下一个时间步的结构初始温度。
5)将结构温度传递给流场计算中,重复步骤3~4,如此迭代。
2 计算结果及分析
2.1 计算模型
1987年,Wieting 等为了研究气动-热-结构耦合效应,对圆柱模型分别进行了实验和仿真数值计算。该实验被后来多次用于验证耦合传热仿真的可靠性。
实验对象为一长直圆管,对该实验进行简化后,使用二维圆管进行仿真数值计算,圆管的外形及网格划分如图2所示。由于流场是上下对称的,所以只取上半部分流场进行计算。本文只关心圆管迎风面处的气动加热情况,因此对背风面处的流动状况不进行讨论,且圆管背风面对计算结果没有影响,所以只取前1/4 圆管进行计算。圆管的内径为24.5 mm,外径为38.1 mm。网格中,为了准确计算壁面处的热流,对靠近壁面处的网格进行了加密处理,使壁面处的网格雷诺数接近于1,流场中靠近壁面的网格第一层高度为3.86×10m。
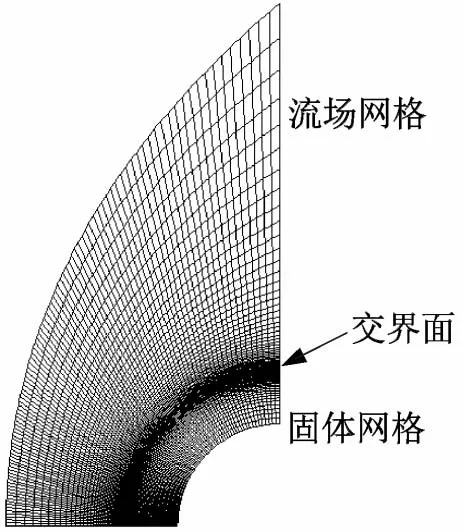
图2 流场和结构网格Fig.2 The grid of flow field and structure
2.2 计算条件
二维圆柱绕流计算中,来流温度=241.5 K,马赫数=6.47,雷诺数=1.31×10m;压力=648.1 Pa,使用层流进行计算。
对于结构部分,实验中材料为321 不锈钢,其热力学参数为:密度=7 920 kg/m,比热=500 J/(kg·K),热传导系数=16.3 W/(m·K),固体结构的初始温度为294.5 K。
2.3 稳态计算
图3为稳态流场中计算得到的热流以驻点热流值为基准进行归一化后的曲线与实验数据之间的对比。从图中可以看出,热流绕圆柱的分布趋势与实验数据吻合很好,但是驻点热流与实验值有一定偏差。本文得到的仿真驻点热流为5.057×10W/m,文献[7]中仿真计算得到的驻点热流为4.82×10W/m,文献[11]计算值为5.41×10W/m。从与其他文献的结果对比中可以看出,文献中的数值模拟和本章的模拟均使用了层流进行计算,本章和其他文献计算结果接近,相差6.5%。
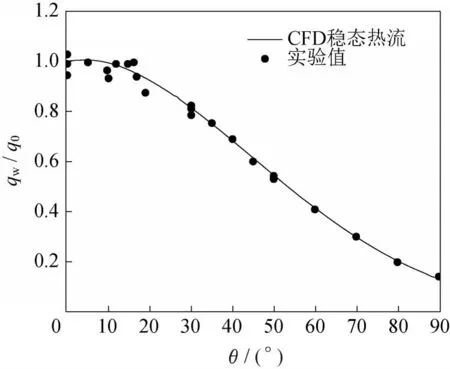
图3 钝头体表面稳态热流比较Fig.3 The steady state heat flux comparison of the blunt body
2.4 迭代耦合
耦合传热得到的结果如图4~图8所示。由于高马赫数气动加热这类问题中,流场的特征时间远远小于结构传热的特征时间,所以先将固体壁面设置为等温壁,计算得到稳态流场和壁面上的热流分布,再以此为初始条件进行流场和固体结构之间的传热耦合计算。
图4为不同时刻下钝头体表面热流分布曲线。随着时间的增加,靠近驻点处温度随着时间的推进上升较快,导致驻点附近温度梯度下降,从而导致归一化热流有下降的趋势。由于圆柱后半部分温度上升不明显,所以50°之后的热流曲线基本没有产生变化。
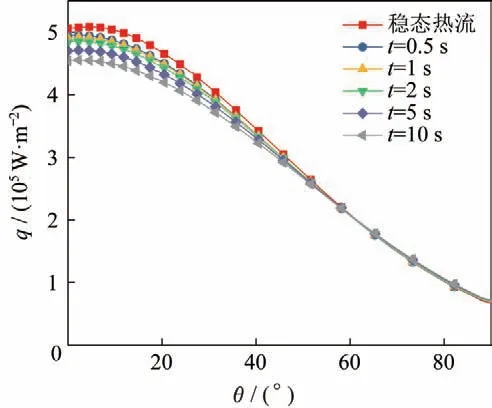
图4 不同时刻表面热流曲线Fig.4 Surface heat flow at different times
图5为热流在进行耦合传热后驻点热流的下降趋势,从图中看出,在刚进行耦合传热的极短时间内,热流有较明显的下降趋势。之后随着时间的增加,驻点温度不断升高,驻点热流下降趋于平缓。可以预见,经过足够长的时间后,热流会达到一个相对稳定的值。
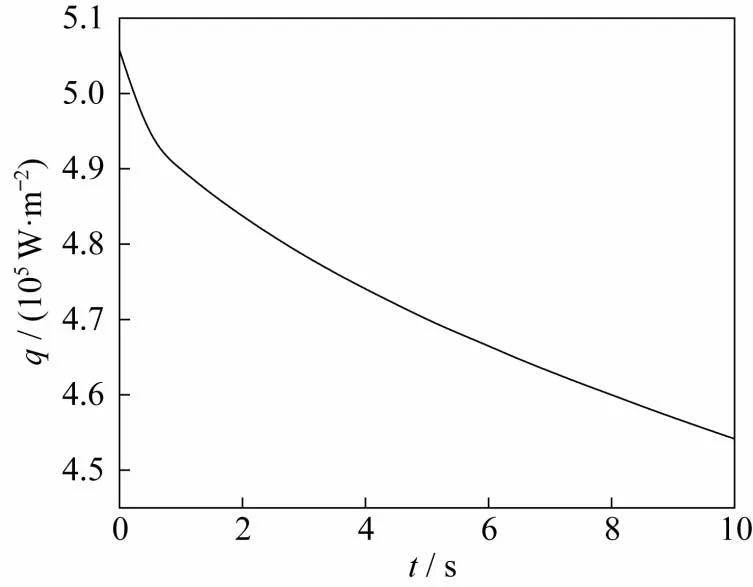
图5 驻点热流随时间变化曲线Fig.5 Stagnation heat flow varying with time
图6为驻点温度随时间变化的曲线,刚开始由于驻点热流较大,温度上升比较快,随着驻点温度上升,热流下降,驻点温度上升速度逐渐降低,同时热流也逐渐降低,最后热流和圆柱表面温度分布都会达到一个平衡状态。本文计算得到的2 s 时刻下驻点温度为395 K,文献[7]计算得到的2 s 时刻下驻点温度为388.9 K,误差仅为1.6%,说明本文耦合传热计算结果是可靠的。
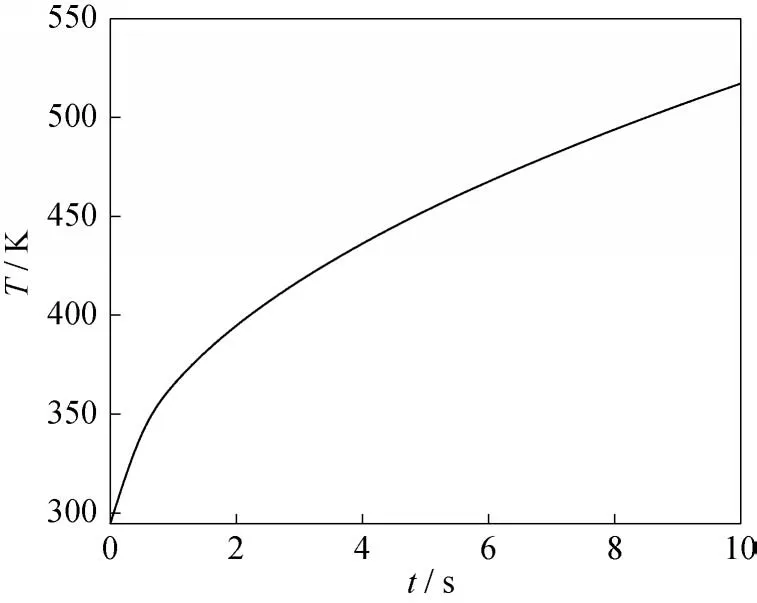
图6 驻点温度变化曲线Fig.6 Stagnation point temperature change
图7为圆柱驻点处沿半径温度分布随时间的变化,在0 时刻即初始条件下,物面温度为294.5 K。随着传热的进行,驻点温度不断升高,且从图中可以看出温度沿半径逐渐向内传播的过程。
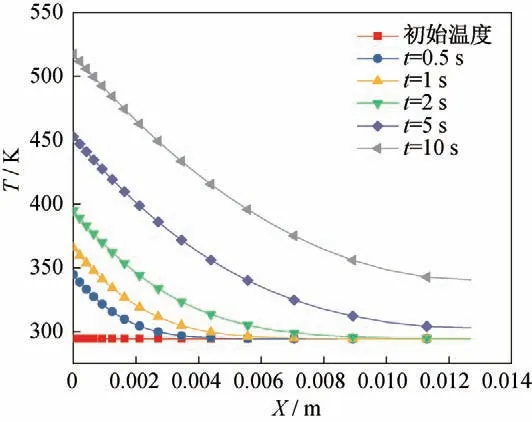
图7 圆柱驻点处沿半径温度变化Fig.7 Temperature variation along the radius at the stagnation point
图8为不同时刻下圆柱表面温度分布,表面初始温度为等温壁294.5 K,在进行耦合传热计算后,物体不断受到流场的气动加热效应,表面温度不断上升。由于驻点处受到的气动加热最严重,所以驻点处温度上升最快,但50°之后的温度曲线变化比较缓慢。这是由于表面角度的增加使得物面受到的气流加热效应大幅下降,所以温度上升缓慢。
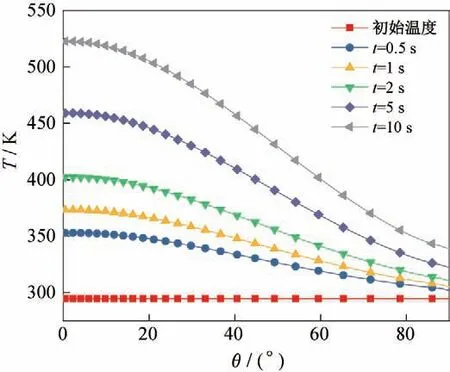
图8 不同时刻表面温度分布Fig.8 Surface temperature distribution at different times
2.5 单向求解
通过分别求解N-S 方程和结构热传导方程,实现了气动加热-传热的单向耦合计算。由于高马赫数飞行下壁面附近流场温度很高,短时间内结构表面温度的上升对于壁面处温度梯度影响不大,所以可以假定在短时间内结构表面热流即为以等温壁为条件的稳态流场下求得的表面热流。然后再将该热流作为结构传热计算的热流边界条件进行传热分析,不考虑结构温度上升对流场的反作用。
实际情况下,随着气动加热和结构传热的进行,结构表面温度会上升,从而导致结构表面热流降低。从图4可以看出,随着时间的增加,表面温度上升还是会导致表面热流下降,从而会影响结构传热。由于使用单向耦合不考虑表面热流随时间的下降,所以计算得到的结构温度相较于实际情况和耦合传热会偏高。
图9和图10分别为2 s 和10 s 时单向求解结构瞬态传热得到的温度场,从图中可以看出,随着传热的进行,温度不断向结构内部进行传导,同时结构表面温度也随时间不断升高。
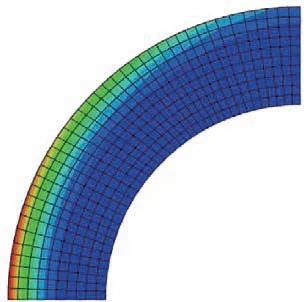
图9 2 s时结构温度分布Fig.9 Structure temperature distribution at 2 s
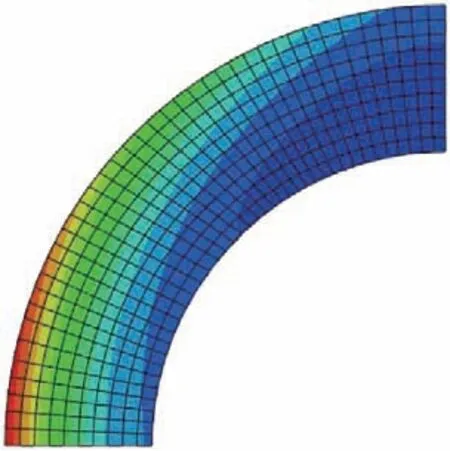
图10 10 s时结构温度分布Fig.10 Structure temperature distribution at 10 s
2.6 计算结果对比
图11为使用单向求解和迭代耦合分别计算得到的驻点热流变化曲线。单向求解进行到2 s时,驻点温度为396.7 K,使用迭代耦合计算得到2 s 时的驻点温度为395 K,两者差距仅为0.43%;在10 s时,迭代耦合和单向求解两种方法计算得到的驻点温度分别为536.12 K 和517.2 K,差距为3.66%。这说明两种计算方法在传热进行后的较短时间内,计算得到的结构温度之间的差距非常小,随着加热时间的增长,两者计算温度差距逐渐增大,迭代耦合计算得到的温度低于单向求解的温度。相比于迭代耦合传热计算,使用单向求解的方法能提高计算的效率,并且在短时间内能保持较高的精度,但是随着传热时间的增加,单向求解的误差会逐渐增加,而迭代耦合计算的结构更加接近实际值。
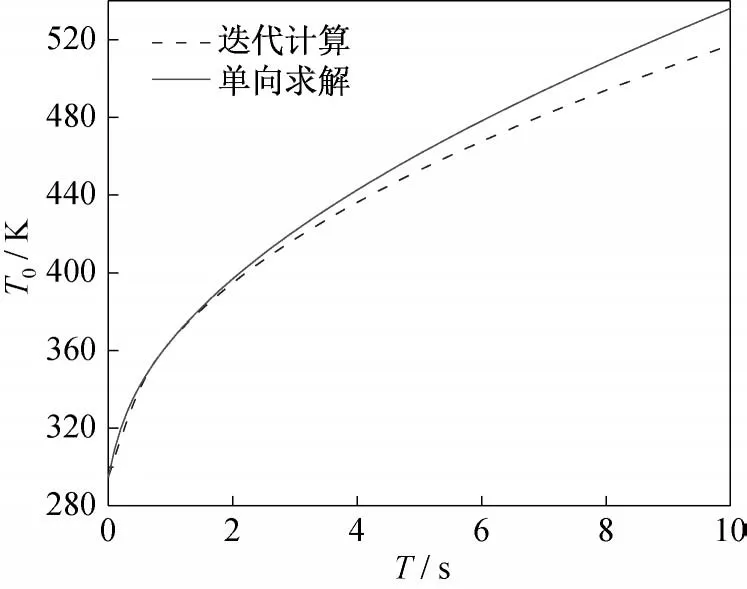
图11 迭代耦合和单向求解不同时刻驻点温度比较Fig.11 The Stagnation point temperatures of iterative coupling and one-way solving methods at different times
3 结 论
本文通过CFD 数值模拟方法求解N-S方程,得到了钝头体表面稳态热流分布,分别用迭代耦合和单向求解的方法模拟了结构内部传热过程,并将两者的结果进行了对比,结论如下:
1)单向求解得到的结构温度要高于迭代耦合计算结果。使用迭代耦合计算方法相比于单向耦合可以更加准确地预测气动加热和结构传热的过程,但迭代耦合需要在每一个时间步内都对流场进行求解,所以迭代耦合计算量会远大于单向耦合。
2)在相同的来流条件下,传热开始后的短时间内,迭代耦合和单向耦合计算的结果相差很小,随着时间的增加,误差逐渐增大。所以在一定的误差许可下,使用单向耦合能极大地提高计算效率,同时得到相对比较准确的结果,但随着时间加长,单向求解误差将逐渐增大。
