一种融合物理规律的经验工程修正算法研究

邓 晨，孔轶男，2，汪 清，2，陈 功，2

（1.中国空气动力研究与发展中心计算所，四川绵阳 621000；2.空气动力学国家重点实验室，四川绵阳 621000）

0 引 言

在飞行器设计初期，气动外形需要反复修改迭代，经济而快速的计算其气动参数十分重要。计算流体动力学（computational fluid dynamics，CFD）方法可以较为准确地计算导弹气动参数，但其计算量太大，飞行器每一次修改气动外形都需要消耗大量的时间成本和人力成本，不适合在设计初期使用；而工程估算算法可以较快速地得到飞行器的空气动力参数和操稳特性，因此广泛应用于初步设计阶段。

工程算法能够借助解析表达式，快速估算气动特性。李通等为研究非对称变化的后掠角对导弹气动特性的影响，利用快速计算软件Missile Datcom 计算了不同条件下导弹的气动参数，并基于此进行了相关分析。何佳丽等针对海鹰2 号，分别采用Datcom 和Fluent软件计算其气动特性，通过对比分析发现，在一定的范围内两种方法均满足工程设计要求，通过对工程算法进行局部修正，可以得到更为精准的气动力系数。朱莹等以小迎角工程算法为基础，提出了一种大迎角下细长旋成体导弹工程计算方法，计算结果较其它估算方法更为准确。

经验工程算法虽然能够快速估算气动特性，但是精度却不尽如人意，需要进行局部修正才能达到足够的精度。如果能够利用CFD 部件气动力数据或者风洞试验数据，对其中的重要参数进行修正拟合，提高其计算精度，对于降低试验代价，完善工程估算方法有积极的意义。

本文主要从两个方面开展研究：一是从部件的角度出发剖析部分气动外形参数和飞行状态变量对气动力系数的影响规律，总结经验公式；二是基于少量CFD 试验数据点修正经验公式的重要参数，达到数据融合目的，减少获得高精度数据试验代价。

1 数据适用性验证

1.1 Datcom数据

Missile Datcom 软件是美国空军力学实验室开发的应用于导弹气动力估算的工程估算软件。它充分利用了美国几十年的风洞试验和飞行试验数据建立典型气动模型，由大量的图表和公式组成，采用了部件组合法、数据模块化和方法模块化的思想，在一定范围内对不同飞行条件下各种气动外形具有较高的精度。

为了验证Datcom的适用性，针对典型轴对称导弹进行计算，分别计算得到Datcom数据和试验数据。该型导弹弹体采用蛋形头部，圆柱形弹身，全弹长细比为18，弹翼和尾翼采用“十”字形布局，翼剖面为菱形，弹翼和尾翼的后掠角分别为45°和57°，单位长度雷诺数为8.2×10，滚转角、侧滑角和舵面偏转角均为0°。Datcom数据和试验数据的升力系数如图1所示。

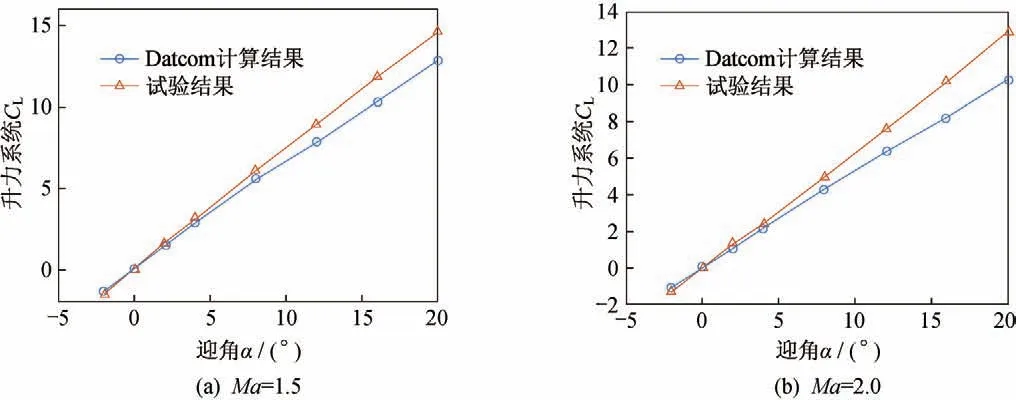
图1 不同马赫数下Datcom数据和试验数据对比Fig.1 Comparison of Datcom data and experimental data at different Mach numbers

由图1可知，在小迎角范围内，Datcom 数据和试验数据结果十分吻合，随着迎角和马赫数的增加，偏差逐渐增大。在一定的精度范围内，Datcom 计算结果有效合理，可以作为建立具有物理意义的工程修正算法的参考。

1.2 CFD数据

一般而言，因为无法获得气动真值，所以很难评判哪一种方式获得的数据最为准确，但是针对本文研究的光弹身外形，通过比较类似外形的飞行试验数据、风洞试验数据和CFD试验数据（见图2），得到如下结果：对于光弹身外形飞行器，CFD能够较为精准的计算出气动数据，CFD数据可以作为修正数据来修正经验公式，以得到计算效率高、代价低且精度高的气动数据。

图2 三种方式结果对比图Fig.2 Comparison of the results of the three methods

2 基于CFD数据的公式修正拟合

Datcom 对于小迎角、小马赫数下的导弹气动特性计算较为准确，但是对于大迎角、高马赫数下的导弹气动特性估算误差较大。基于此，本文研究的对象为马赫数大于5的高超声速飞行器，以法向力系数为例，利用其少量CFD数据进行修正拟合，分别总结每个部件的修正经验公式。

2.1 CFD计算数据

导弹采用双截锥构型，“X”型尾翼布局，基本气动外形和参数如图3所示，单位为mm。

图3 气动外形和参数Fig.3 Aerodynamic configuration and parameters

利用国产CFD 计算软件NNW-FlowStar 进行数值计算，计算状态马赫数分别为5、7、11，迎角0°～20°，网格如图4所示。

图4 CFD计算网格图Fig.4 CFD calculation grid diagram

得到计算结果如表1所示。

表1 CFD计算结果Tab.1 CFD calculation results

2.2 具有物理意义的经验公式修正拟合

将CFD 计算结果分为训练集和测试集，利用训练集中样本数据对部件经验公式进行修正拟合，然后再利用测试集数据进行验证。将每个飞行状态前3 个迎角测得的数据作为训练数据，剩余3 个迎角状态测得的数据作为测试数据。以图5所示部件组合的形式进行修正拟合，其中，飞行条件只考虑了迎角和马赫数的影响，其余高度等因素未考虑，故未列出。

图5 导弹部件组合形式Fig.5 The combination of missile components

根据部件组合法，导弹的法向力系数主要由弹体的法向力系数、弹翼的法向力系数和翼体干扰组成，可表达为

式中：K为翼体干扰系数；为迎角；为弹翼面积；为弹体最大横截面积。

弹体的法向力系数包含弹头（含连接圆柱段弹身）、弹尾法向力系数和黏性法向力系数，如图6所示。

图6 弹体法向力系数组成Fig.6 The composition of the normal force coefficient of the missile body

弹头（含连接圆柱段弹身）的线性法向力系数主要与弹身长细比、弹头长细比、来流马赫数和弹头外形等有关，针对本文对象，可表示为

式中：C为法向力系数斜率，利用CFD数据进行修正拟合得到，计算式为

弹尾法向力系数主要和弹尾形状、弹尾收缩比和来流马赫数等有关，可表示为

式中：C为弹尾法向力系数斜率；为弹尾直径；为弹身最大横截面直径；为考虑弹体尾部上附面层变厚以及气流分离的影响而引入的修正系数。

因为本文对象无收缩或扩张尾部，所以并未对其参数进行修正，取=0。

弹体黏性法向力系数和弹身长细比、弹头长细比、来流马赫数和弹头外形等有关，计算式为

式中：为物形因子；为横流干扰因子。

和经CFD 数据修正拟合之后得到，计算式分别为

弹翼法向力系数包含弹翼线性法向力系数和弹翼黏性法向力系数，如图7所示。

图7 弹翼法向力系数组成Fig.7 The composition of the normal force coefficient of the wing

弹翼的线性法向力系数主要和外露翼展弦比、翼型和后掠角等有关。本文对象为大展弦比弹翼，具有六角形翼型，前缘后掠型机翼（定义见式（8））。超音速下大展弦比机翼线性法向力系数如式（9）所示。

式中：为法向马赫数；C由CFD 数据进行修正拟合得到，计算式为

弹翼的黏性法向力系数和来流马赫数、外露翼展弦比等有关，计算式为

式中：为横流因子，由CFD 数据进行修正拟合得到，计算式为

洗流、压强重新分布及翼体连接区域内局部马赫数的改变等因素，导致翼体组合体的气动力特性有别于单独部件的气动特性，因此需要考虑翼体之间的相互干扰。

翼体干扰修正系数K计算式为

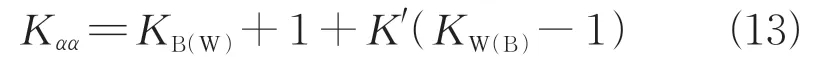
式中：'为考虑非线性影响的经验修正因子，计算式为

式中：为来流马赫数；为弹翼对弹体的干扰升力与单独外露弹翼升力之比；为有弹体影响下，外露弹翼升力与单独外露弹翼升力之比，计算式为

式中：为弹体半径；'为毛弹翼的翼展。

2.3 结果对比

利用CFD 预测数据集对经验修正公式得到的数据进行对比，并对比分析了Datcom 计算结果，得到3种马赫数下法向力系数结果如图8所示。

图8 三种计算方法得到的不同马赫数下的法向力系数Fig.8 Normal force coefficients obtained by three calculation methods under different Mach numbers

分析图8可知，对比Datcom 计算结果，修正公式计算结果更接近于CFD数据，精度更高。为了更加准确地说明结果，设定平均误差为

式中：和分别为不同计算方式的预测值。得到两种计算方法与CFD计算结果误差如表2所示。

表2 计算误差比较Tab.2 Computational error comparison

表2定量地说明了修正计算公式数据更接近于CFD 数据，可以用少量CFD 数据点来修正拟合经验公式，得到具有物理意义的精度更高的经验修正公式。推广而言，如果使用更高精度的气动数据，则修正的公式计算结果会更加准确，这种算法在原理上是可行的。

3 结束语

本文在传统直接利用工程算法计算气动力系数的基础上，采用了少量CFD部件数据对公式进行修正拟合，得到了融入物理意义且计算精度更高的工程修正算法。主要在以下两个方面进行了创新和发展：

1）从部件的层次对工程算法进行剖析，对部件的工程计算公式进行总结和修正，从原理上解释了方程的组成，让算法融合了物理规律，更真实、更可信；

2）利用少量CFD 部件气动力数据作为训练数据，得到的预测模型精度满足要求，不再需要大量的CFD 数据来建立模型，大大降低了试验代价，同时也证明了该方法是可行的。