一类离散综合控制系统的保性能控制
2022-09-28孙凤琪
孙 凤 琪
(吉林师范大学数学与计算机学院,吉林 四平 136000)
0 引言
在控制系统中,由于使得系统不稳定和系统性能变弱的因素诸多,因此要求在能够保证鲁棒稳定的同时,还要使系统的性能指标满足一定的要求,即保性能控制[1].对于不确定离散时滞奇异摄动控制系统,如何设计出一个高效合理的保性能控制器,使得在综合指标前提条件下系统的性能指标始终不会超过某个上限,这是一个具有挑战性的研究课题,引起了非常多学者的关注[2-4].目前,关于连续系统的保性能控制研究成果较多,但是,针对不确定离散时滞奇异摄动控制系统保性能控制的研究成果尚少.
文献[5]第一次将保成本控制由连续系统推广到离散系统,对含有不确定性和时间滞后的离散系统进行分析,最后得到了存在无记忆状态反馈控制器的条件.文献[6-8]同样对离散系统开展了研究,选取了包含参数不确定性的滞后系统,得出了保性能控制器在离散系统中存在的最佳状态.文献[9]对于具有非线性的离散2维系统进行保成本控制分析,考虑了控制器可能出现的无记忆和记忆两种状态,由Lyapunov稳定性定理得出系统是鲁棒稳定的,并以线性矩阵不等式方法为途径,得到了系统存在保性能控制器的条件.然而,文中并没有考虑系统中可能存在时变时滞状态的情形.
目前,保性能控制在不确定连续时滞系统中的探究已非常详细,研究成果颇丰.在离散系统中保性能控制理论成果也较多,但都不同程度地存在系统单一以及研究方法过于保守的问题[15-16],且针对时滞摄动离散系统的相关文献仍尚少.因此,如何选取新的方法使不确定离散时滞奇异摄动控制系统的保性能控制问题得到有效解决,需要广大学者做进一步研究.
本文以现有的理论成果为基础,将系统中的时滞设定为时变状态,在系统矩阵中添加奇异摄动和不确定性,对不确定离散时滞奇异摄动控制系统进行保性能控制分析,给出了闭环系统达到渐近稳定状态时系统性能指标的更小上界和系统存在状态保性能控制器的具体条件.
通过线性矩阵分析方法和交叉项界定方法,利用李亚普诺夫稳定性理论,本文研究了不确定离散时滞奇异摄动控制系统的保性能控制问题,设计依赖奇异摄动参数的新的性能指标,推出了保性能控制率以及较小的性能指标上界.
1 预备知识
考虑以下带有控制输入的离散不确定时滞奇异摄动控制系统:
(1)
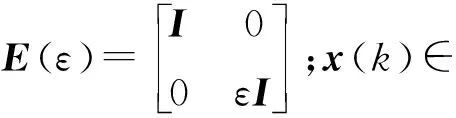
0≤d(k)≤τ,
(2)
τ为已知常数;F(k)∈i×j是不确定参数矩阵,
FT(k)F(k)≤I.
(3)
定义性能指标如下:
(4)
其中S和R是待定的对称正定加权矩阵.
设计状态反馈控制器
u*(k)=Kx(k),
(5)
其中K是未知的控制器增益矩阵,则闭环系统成为
E(ε)x(k+1)=[A+DF(k)E1]x(k)+[Ad+DF(k)Ed]x(k-d(k))+BKx(k)=
[A+BK+DF(k)E1]x(k)+[Ad+DF(k)Ed]x(k-d(k)),
(6)
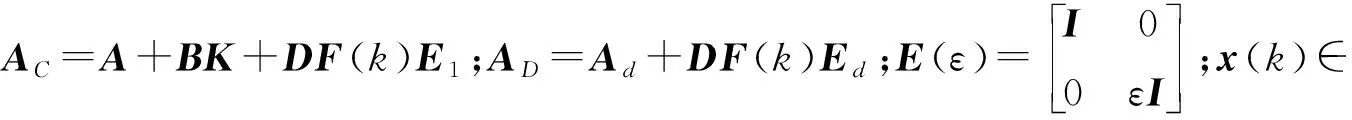
本文所得结论均在满足文献[17]引理1的条件下成立.
2 时滞依赖的保性能控制
(7)
(8)
则系统(1)的状态反馈保性能控制器存在,相应的保性能控制律为
性能指标上界为
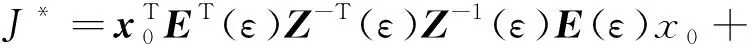
且闭环系统性能指标(4)满足J≤J*.
证明定义如下的Lyapunov泛函:
V(x(k))=V1(k)+V2(k)+V3(k).
其中:
V1(k)=xT(k)ET(ε)Z-T(ε)Z-1(ε)E(ε)x(k),
这里Q和M为对称正定矩阵,即QT=Q>0,MT=M>0.
由文献[17]引理2,得:
从而V(x(k))为正定的L-K泛函.将V(x(k))沿着闭环系统(6)的任意轨迹进行差分,得到ΔV(k)≤ξT(k)G(ε)ξ(k),其中:
(9)
这里:
Σ(ε)=Z-T(ε)Z-1(ε)+Z-T(ε)QZ-1(ε)+(1-τ)M;
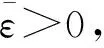
AC=A+BK+DF(k)E1;
AD=Ad+BK1+DF(k)Ed.
类似于文献[17]中定理2的证明,对G(ε)<0消去不确定性并进行线性化处理.若记
则G(ε)<0等价于
以上过程均可逆,故
ΔV(k)≤ξT(k)G(ε)ξ(k)<0,
因此,闭环系统(6)渐近稳定.
由(9)式得:
ΔV(k)<-xT(k)[Z-T(ε)SZ-1(ε)+KTRK]x(k)<0;
-ΔV(k)>xT(k)[Z-T(ε)SZ-1(ε)+KTRK]x(k).
将上式两边从0到∞对k求和,并利用系统的稳定性可知V(x(∞))=0,故
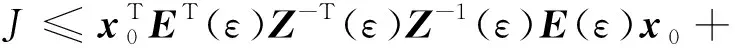
3 时滞独立的保性能控制

(10)
(11)
则系统(1)的状态反馈保性能控制器存在,相应的保性能控制律为
性能指标上界为
且闭环系统性能指标(4)满足J≤J*.
定理2的证明过程与定理1类似,此处略去.
4 算例
考虑满足如下非标准情形的不确定离散时滞奇异摄动控制系统(1)和性能指标(4),其中:
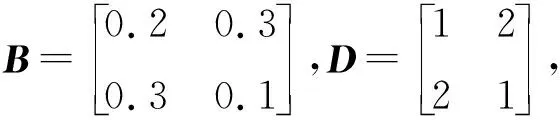
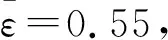
Z1=0.164 8,Z2=0.124 9,Z3=0.378 4,Z4=0.459 8,Z5=0.212 3,γ=2.412 6,
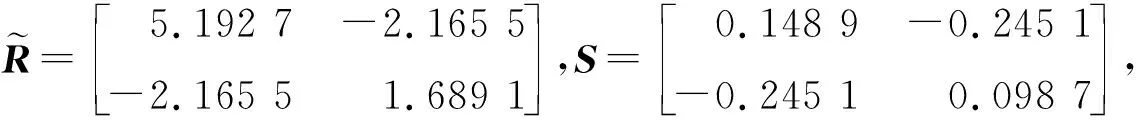
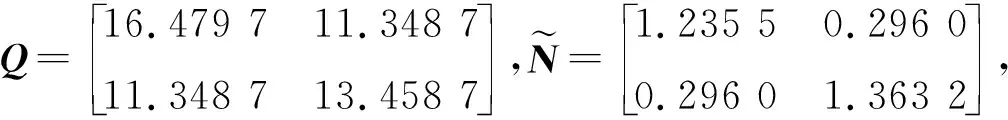
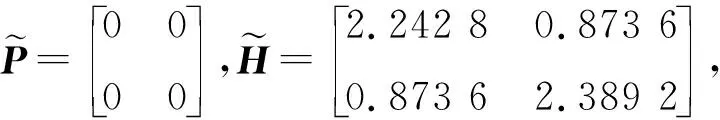
则
即为系统(1)的状态反馈保性能控制律,性能指标上界为
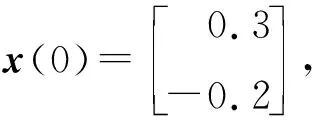

表1 保性能控制性能指标对比
定理1具有较大的奇异摄动参数上界值0.55,并且保性能控制区间在(0,0.55],扩大了闭环系统的渐近稳定范围,性能指标上界值J*=9.853 7比文献的10.700 6也相对更小.
综上数值样例表明,本文所得定理的保性能控制条件具有可行性,控制方式有效,进一步拓宽和完善了保性能控制理论体系.其线性矩阵不等式保性能控制条件形式简单易行,并且适用于标准和非标准情形.相比较而言,本文的控制效果具有一定的优越性,研究结果具有一定的理论意义和实际应用价值.
5 结论
在近几年中,保性能控制问题受到了越来越多学者的关注,在众多学者的共同努力下,已经形成了比较系统的理论体系.本文创新之处在于:
(1) 选取了新的综合控制系统保性能控制研究;
(2)重新定义了性能指标,以及一个新的李亚普诺夫泛函;
本文对于不确定离散时滞奇异摄动控制系统保性能控制的研究,可以为相关控制问题研究提供理论参考.对于记忆状态反馈保性能控制设计,是下一步需要解决的问题.
