含参Ky Fan不等式与对偶问题解映射的Lipschitz连续性
2022-09-28孟旭东蒋海英曾慧平
孟旭东,蒋海英,曾慧平
(1.南昌航空大学科技学院文理学部,江西 共青城 332020;2.江西交通职业技术学院基础教学部,江西 南昌 330013)
1972年,Ky Fan介绍了一类著名的不等式,称为Ky Fan不等式,在数学领域一般简记KFI[1-2].到目前为止,Ky Fan不等式在不等式分析和优化问题研究中起着重要作用.一批学者已经讨论了各种形式Ky Fan不等式解的存在性问题[3-6].Ky Fan不等式解的稳定性是优化理论与应用研究中的热点话题.一般而言,Ky Fan不等式含参解集具有一定的品性,比如上半连续性、下半连续性、连续性、Lipschitz连续性、Hölder连续性等[7-16].
受以上文献启发,本文在赋范线性空间中研究含参Ky Fan不等式与对偶问题解映射的Lipschitz连续性.
1 预备知识
设X,Λ,M为赋范线性空间,‖·‖和d(·,·)分别表示范数和距离,K:Λ→2X{∅}为闭凸集值映射,f:X×X×M→为实值映射.
对每个(λ,μ)∈Λ×M,考虑含参Ky Fan不等式(记为PKFI):找x0∈K(λ),使得
f(x0,y,μ)≥0,∀y∈K(λ).
对每个(λ,μ)∈Λ×M,考虑含参对偶Ky Fan不等式(记为PDKFI):找x0∈K(λ),使得
f(y,x0,μ)≤0,∀y∈K(λ).
对每个(λ,μ)∈Λ×M,记(PKFI)与(PDKFI)的有效解集分别为S(λ,μ)和D(λ,μ),即
S(λ,μ)∶={x∈K(λ)|f(x0,y,μ)≥0,∀y∈K(λ)},
D(λ,μ)∶={x∈K(λ)|f(y,x0,μ)≤0,∀y∈K(λ)}.
本文假设对每个(λ,μ)∈Λ×M,S(λ,μ)≠∅,D(λ,μ)≠∅,讨论S(·,·),D(·,·)在Λ×M上的Lipschitz连续性.
定义1 设X为赋范线性空间,B⊂X为非空凸子集,g:X→为实值映射.
(1) 称g在B上为强凸映射,当且仅当对任何x,y∈B及t∈(0,1),有
g(tx+(1-t)y)≤tg(x)+(1-t)g(y)-t(1-t)‖x-y‖.
(2) 称g在B上为强凹映射,当且仅当对任何x,y∈B及t∈(0,1),有
tg(x)+(1-t)g(y)≤g(tx+(1-t)y)-t(1-t)‖x-y‖.
定义2[15]设X为赋范线性空间,B⊂X为非空子集,g:X×X→为实值映射.
(1) 称g在B×B上为单调映射,当且仅当对任何x,y∈B,x≠y,有
g(x,y)+g(y,x)≤0.
(2) 称g在B×B上为伪单调映射,当且仅当对任何x,y∈B,x≠y,有
g(x,y)≥0⟹g(y,x)≤0.
注1 由g在B×B上单调可知g在B×B上必伪单调,但反之不然,见下面例1.
例1 设X=,B=(0,+∞),g:X×X→定义为g(x,y)=y(y-x).对任何x,y∈B,x≠y,若g(x,y)=y(y-x)≥0,则g(y,x)=x(x-y)≤0,故g在B×B上为伪单调.但是
g(x,y)+g(y,x)=(x-y)2>0,
故g在B×B上不是单调映射.
定义3[16]设X,Λ,M为赋范线性空间,B⊂X为非空子集,
(1) 称实值映射g:X→在x0∈X处为l-Lipschitz连续,当且仅当存在l>0,及x0邻域N(x0)⊂X,使得对任何的x1,x2∈N(x0),有
|g(x1)-g(x2)|≤l‖x1-x2‖.
(2) 称集值映射K:Λ→2X{∅}在λ0∈Λ处为h-Lipschitz连续,当且仅当存在h>0,及λ0邻域U(λ0)⊂Λ,使得对任何的λ1,λ2∈U(λ0),有
K(λ1)⊂K(λ2)+h‖λ1-λ2‖B0,
其中B0为X中的闭单位球.
(3) 对每个μ0∈M,称实值映射f:B×B×M→在μ处关于B×B为一致k-Lipschitz连续的,当且仅当存在k>0,及μ0的邻域V(μ0)⊂M,使得对任何的μ1,μ2∈V(μ0),及x1,x2∈B,x1≠x2,有
|f(x,y,μ1)-f(x,y,μ2)|≤k‖μ1-μ2‖.
2 Lipschitz连续性
设A,B⊂X为非空子集,定义

对每个(λ0,μ0)∈Λ×M,存在(λ0,μ0)的邻域U(λ0)×V(μ0)⊂Λ×M,满足:
(H1)K(·)在λ0处为l0-Lipschitz连续;


(H4) 对任何的μ∈V(μ0),f(·,·,μ)在K(U(λ0))×K(U(λ0))上为伪单调映射;
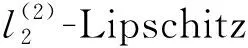
(H6) 对任何的μ∈V(μ0),f(·,·,μ)在μ处关于K(U(λ0))×K(U(λ0))为一致l3-Lipschitz连续;
(H7) 对任何的x∈K(U(λ0))及μ∈V(μ0),f(x,x,μ)=0.
定理1 若(PKFI)满足(H1)—(H4),(H6)及(H7),则:
(1) 在U(λ0)×V(μ0)上,(PKFI)的解映射为单值映射;
(2) 对任何的(λ1,μ1),(λ2,μ2)∈U(λ0)×V(μ0),有
d(S(λ1,μ1),S(λ2,μ2))≤L1‖λ1-λ2‖+L2‖μ1-μ2‖,
(1)
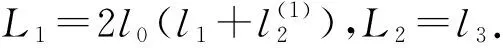
证明设(λ1,μ1),(λ2,μ2)∈U(λ0)×V(μ0),要证(1)式成立,分以下3步论证:
第1步任取x11∈S(λ1,μ1),x21∈S(λ2,μ1),则
‖x11-x21‖≤L1‖λ1-λ2‖,
(2)
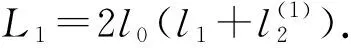
不失一般性,不妨假设x11≠x21.据x11,x21为(PKFI)的解知,对任何y∈K(λ1),z∈K(λ2),有
min(f(x11,y,μ1),f(x21,z,μ1))≥0.
(3)
由条件(H1)知,对l0>0,存在x1∈K(λ1),x2∈K(λ2),使得
max(‖x11-x2‖,‖x21-x1‖)≤l0‖λ1-λ2‖.
(4)
在(3)式中,令z=x2,有
f(x21,x2,μ1)≥0.
(5)
据条件(H4)得
-f(x2,x21,μ1)≥0.
(6)
注意到K(λ1)为X的凸子集,则对任何的t∈(0,1),有(1-t)x11+tx1∈K(λ1).
在(3)中,取y=(1-t)x11+tx1,得
f(x11,(1-t)x11+tx1,μ1)≥0.
(7)
再由f的强凸性并注意到f(x11,x11,μ1)=0,可知
f(x11,(1-t)x11+tx21,μ1)≤tf(x11,x21,μ1)-t(1-t)‖x11-x21‖.
(8)
由(6)—(8)式,
t(1-t)‖x11-x21‖≤
tf(x11,x21,μ1)-f(x11,(1-t)x11+tx21,μ1)≤
t(f(x11,x21,μ1)-f(x2,x21,μ1))+f(x11,(1-t)x11+tx1,μ1)-
f(x11,(1-t)x11+tx21,μ1).
由条件(H2)与(H3)中f的Lipschitz连续性及(4)式得
从而
(9)
类似地,有
(10)
结合(9)与(10)式,有
‖x21-x11‖≤L1‖λ1-λ2‖,
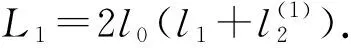
第2步对任何的x21∈S(λ2,μ1),x22∈S(λ2,μ2),有
‖x21-x22‖≤L2‖μ1-μ2‖.
(11)
其中L2=l3.
由于x21,x22为(PKFI)的解,故对任意y,z∈K(λ2),有
min{f(x21,y,μ1),f(x22,z,μ2)}≥0.
(12)
注意到K(λ2)为X的凸子集,则对任何的t∈(0,1),有(1-t)x21+tx22∈K(λ2).在(12)式中,取y=(1-t)x21+tx22,则
f(x21,(1-t)x21+tx22,μ1)≥0.
(13)
据f的强凸性并注意到f(x21,x21,μ1)=0,结合(13)式,有
t(1-t)‖x21-x22‖≤tf(x21,x22,μ1)-f(x21,(1-t)x21+tx22,μ1)≤tf(x21,x22,μ1).
(14)
再由(14)式知
(1-t)‖x21-x22‖≤f(x21,x22,μ1).
(15)
另一方面,在(12)式中,令z=(1-t)x21+tx22,类似(15)式的分析可知
t‖x21-x22‖≤f(x22,x21,μ2).
(16)
根据条件(H4),
t‖x21-x22‖≤-f(x21,x22,μ2).
(17)
从而由(15)与(17)式得
‖x21-x22‖≤f(x21,x22,μ1)-f(x21,x22,μ2)=
|f(x21,x22,μ1)-f(x21,x22,μ2)|≤L2‖μ1-μ2‖,
其中L2=l3.
第3步对任何的x11∈S(λ1,μ1),x22∈S(λ2,μ2),由(2)与(11)式有
‖x11-x22‖≤‖x11-x21‖+‖x21-x22‖≤L1‖λ1-λ2‖+L2‖μ1-μ2‖,
则
d(S(λ1,μ1),S(λ2,μ2))≤L1‖λ1-λ2‖+L2‖μ1-μ2‖.
(18)
在(18)式中,令λ1=λ2,μ1=μ2,对任意(λ1,μ1)∈U(λ0)×V(μ0),有S(λ1,μ1)={0}.
类似地,对任意(λ2,μ2)∈U(λ0)×V(μ0),有S(λ2,μ2)={0}.所以,在U(λ0)×V(μ0)上,(PKFI)的解映射为单值映射且(1)式成立.
综上,结论得证.
定理2 若(PDKFI)满足(H1)—(H2),(H4)—(H7),则:
(1) 在U(λ0)×V(μ0)上,(PDKFI)的解映射为单值映射;
(2) 对任何的(λ1,μ1),(λ2,μ2)∈U(λ0)×V(μ0),有
d(D(λ1,μ1),D(λ2,μ2))≤K1‖λ1-λ2‖+K2‖μ1-μ2‖,
(19)

证明设(λ1,μ1),(λ2,μ2)∈U(λ0)×V(μ0),要证(19)式成立,分以下3步论证.
第1步任取x11∈D(λ1,μ1),x21∈D(λ2,μ1),则
‖x11-x21‖≤K1‖λ1-λ2‖,
(20)
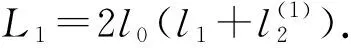
max{f(y,x11,μ1),f(z,x21,μ1)}≤0.
(21)
由条件(H1),对l0>0,存在x1∈K(λ1),x2∈K(λ2),使得
max(‖x11-x2‖,‖x21-x1‖)≤l0‖λ1-λ2‖.
(22)
在(21)式中,令z=x2,有
f(x2,x21,μ1)≤0.
(23)
据条件(H4)得,
f(x21,x2,μ1)≥0.
(24)
注意到K(λ1)为X的凸子集,则对任何的t∈(0,1),有
(1-t)x11+tx1∈K(λ1).
在(21)式中,取y=(1-t)x11+tx1,得
f((1-t)x11+tx1,x11,μ1)≤0.
(25)
再由f的强凹性并注意到f(x11,x11,μ1)=0,
f((1-t)x11+tx21,x11,μ1)≥tf(x21,x11,μ1)+t(1-t)‖x11-x21‖.
(26)
再由(24)—(26)式知,
t(1-t)‖x11-x21‖≤f((1-t)x11+tx21,x11,μ1)-tf(x21,x11,μ1)≤
f((1-t)x11+tx21,x11,μ1)-tf(x21,x11,μ1)≤
f((1-t)x11+tx21,x11,μ1)-f((1-t)x11+tx1,x11,μ1)+t(f(x21,x2,μ1)-f(x21,x11,μ1)).
由条件(H2)与(H3)中f的Lipschitz连续性及(22)式得
则
(27)
类似地,有
(28)
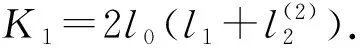
第2步对任意x21∈D(λ2,μ1),x22∈D(λ2,μ2),必有
‖x21-x22‖≤K2‖μ1-μ2‖,
(29)
其中K2=l3.
由x21,x22为(PDKFI)的解可知,对任意y,z∈K(λ2),有
max(f(x21,y,μ1),f(x22,z,μ2))≤0.
(30)
注意到K(λ2)为X的凸子集,则对任意t∈(0,1),得(1-t)x21+tx22∈K(λ2).在(30)式中,取y=(1-t)x21+tx22,有
f(x21,(1-t)x21+tx22,μ1)≤0.
(31)
由f的强凹性,注意到f(x21,x21,μ1)=0,并结合(30)式,有
t(1-t)‖x21-x22‖≤
f(x21,(1-t)x21+tx22,μ1)-tf(x21,x22,μ1)≤-tf(x21,x22,μ1).
(32)
由(32)式知
(1-t)‖x21-x22‖≤-f(x21,x22,μ1).
(33)
另一方面,在(30)式中,令z=(1-t)x21+tx22,类似(33)式的分析可知
t‖x21-x22‖≤-f(x22,x21,μ2).
(34)
再由条件(H4),
t‖x21-x22‖≤f(x21,x22,μ2).
(35)
由(33)与(35)式有
‖x21-x22‖≤f(x21,x22,μ2)-f(x21,x22,μ1)=
|f(x21,x22,μ2)-f(x21,x22,μ1)|≤K2‖μ1-μ2‖,
其中K2=l3.
第3步对任何的x11∈D(λ1,μ1),x22∈D(λ2,μ2),由(20)与(29)式有
‖x11-x22‖≤‖x11-x21‖+‖x21-x22‖≤K1‖λ1-λ2‖+K2‖μ1-μ2‖,
从而
d(D(λ1,μ1),D(λ2,μ2))≤K1‖λ1-λ2‖+K2‖μ1-μ2‖.
(36)
在(36)式中,令λ1=λ2,μ1=μ2,对任何的(λ1,μ1)∈U(λ0)×V(μ0),有D(λ1,μ1)={0}.
类似地,对任何的(λ2,μ2)∈U(λ0)×V(μ0),有D(λ2,μ2)={0}.所以,在U(λ0)×V(μ0)上,(PDKFI)的解映射为单值映射且(19)式成立.
