基于可编程电源的数模动模混合仿真系统研究

李振兴，林龙剑，冷 凤，翁汉琍，李 飞

基于可编程电源的数模动模混合仿真系统研究

李振兴1,2，林龙剑1，冷 凤3，翁汉琍1，李 飞1

(1.梯级水电站运行与控制湖北省重点实验室(三峡大学)，湖北 宜昌 443002；2.三峡大学电气与新能源学院，湖北 宜昌 443002；3.强电磁工程与新技术国家重点实验室(华中科技大学)，湖北 武汉 430074)

为满足现代电力系统实时仿真的发展需求，提出一种基于可编程电源的数模动模混合仿真系统。利用动模实验室搭建动模仿真系统，并在RTDS中搭建39节点系统作为数字仿真系统模型，结合以理想变压器模型算法作为功率接口算法的接口系统，形成一个800 V/345 kV的动模数模混合实时仿真系统实验平台。在研究混合仿真接口两端系统延时对系统稳定性和准确性影响基础上，提出用二阶相位超前环节对下发通道和上传通道的接口延时进行相位补偿，以提高系统稳定性和准确性。通过对所搭建的数模动模混合仿真系统的实验，并与纯数字仿真进行对比分析，进一步验证了混合仿真系统的有效性。

数模混合实时仿真；ITM接口算法；相位补偿；纯数字仿真

0 引言

随着超高压、特高压交直流混合输电、新能源发电和微电网配电等多种发配电方式的不断出现[1]，传统电网向着更智能、更灵活的方向发展[2]，以及各种电力电子设备[3]、新型保护控制装置[4]和控制方法[5]的测试与应用，现代电力系统中各个环节特性及其相互作用机理都发生了深刻变化。为保证大规模、跨区域的交直流电网的安全可靠运行，需要对电力系统全方位开展尽可能合乎实际的实时仿真[6]。

目前对于实时电力系统仿真的研究，既有采用动模实验室进行物理动态模拟仿真和实际工程应用研究[7]，也有通过建立实时数字仿真模型进行研究[8]。随着实时数字仿真器RTDS、HYPSIM、ARENE、DDRTS、ADPSS的出现[9]，实时数字仿真器在数模混合仿真系统中(以下称为数模动模仿真系统)的应用越来越多。实时数字仿真建模效率和灵活度高，可以实现较大规模的实时全数字仿真，缺点是对于新研发的电力设备模型搭建时间长，数字仿真系统所建数字模型反映的系统特性有限，且对于高频段仿真困难，仿真的结果也受模型的准确性以及仿真步长的影响。动模仿真系统由动模实验室中真实的物理元件搭建而成，其一次、二次设备相连接，优点是仿真过程连续、直观，无论是高频还是低频都可以得到准确的模拟，缺点是占地面积大且模型搭建周期长[10]，而且可以仿真的节点相对大电网而言非常少，仿真规模小。实时数字仿真系统和物理动态模拟仿真系统在数学上是统一的，均使得各自系统和模拟的系统在数学上满足相同的微分方程和代数方程组[11]。

实时数字仿真和物理动态模拟仿真的混合仿真又称功率硬件在环(Power Hardware-in-The-Loop, PHTL)[12]仿真，接口系统是数模动模混合仿真研究中的核心问题[13]。文献[14]利用传递函数研究了当前主要采用的5种接口算法的稳定性。文献[15]推导出了4种接口算法的统一形式，并提出了混合仿真的“帧—步长时序”。文献[16]采用理想变压器模型法将数模动模混合仿真技术应用于高压直流输电工程中。文献[17]选择电力电子变换器作为物理侧，在RTDS中建模作为数字子系统，提出了通用型大功率数模混合实时仿真系统架构。文献[18]提出了一种数字物理混合仿真相位校正方案，可以对因接口系统产生的延时进行补偿，提高系统的准确性和稳定性；但仿真建立在虚拟的物理元件上，可信度尚不明确。

1 数模动模混合仿真系统的架构

1.1 实时数字模拟仿真系统

本文设计的数模动模混合仿真系统的信号构架如图1所示。本文采用先进的RTDS(Real Time DigitalSimulator)作为数字模拟系统仿真平台，其硬件采用IBM POWER8处理器，结合处理器并行技术计算方式，强大的计算能力使其可进行大规模电网实时数字仿真，仿真步长为50 μs[19-20]。由于RTDS通过下发通道和上传通道与动模仿真系统实现信号交互，需要配置输入输出板卡，即GTAI(Giga- Transceiver Analogue Input)和GTAO(Giga- Transceiver Analogue Output)板卡，完成数字量与模拟量的转换。为了充分利用RTDS的信号处理和控制功能，本文对RTDS搭建的数字模型输入输出信号进行处理，设置低通滤波器、比例环节和零漂校正等处理单元，可以实现更加稳定和准确的仿真实验。

1.2 物理动态模拟仿真系统

物理动态模拟仿真实验室搭建的动模模型简称为动模仿真系统。接口系统直接与物理动态模拟仿真系统的主回路相连接，存在实际电压、电流交换和功率吞吐问题[14]。动模模型参数一般都是按照与实际系统比例缩小而建立的实际物理模型，其额定电压和功率水平具有固定不变的特性，可以真实地反映所仿真的系统特性[21]。

1.3 功率接口系统

功率接口系统作为数模动模混合仿真系统的连接部分，其稳定性和准确性是整个系统设计的核心部分。目前普遍采用的接口算法都是基于替代定理，主要的接口算法包括理想变压器模型(ITM)法、时变一阶近似(TFA)、传输线模型(TLM)、部分电路幅值(PCD)法和阻尼阻抗(DIM)法[18,22]。在混合仿真系统中，根据不同的仿真条件和需要，可以选择不同的接口算法实现混合仿真的接口系统，以提高实时仿真结果的准确性和可靠性。数字仿真系统和动模仿真系统两者通过接口系统的下发通道和上传通道连接形成闭环的数模动模混合仿真系统，如图1所示。本文使用上位机中RSCAD软件对电力系统进行数字建模，RTDS实时计算，再经过下发通道输出参考电压信号作为可编程电源输入信号。接口系统运行机理为接收输入的参考信号，经过追踪放大处理，在其端口得到对应波形相同的电压(或电流)量。

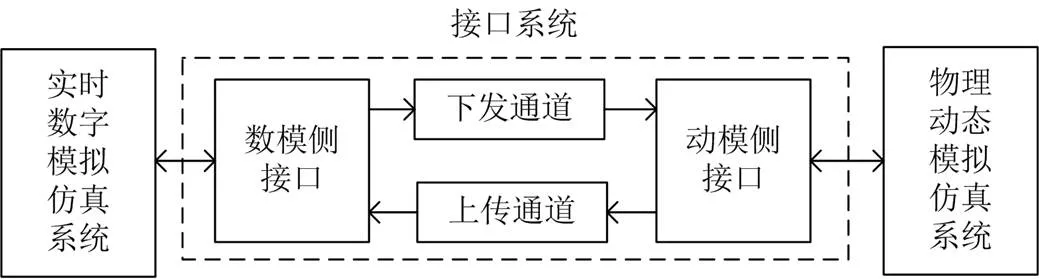
图1 数模动模混合仿真系统架构

2 数模动模混合仿真接口系统设计

2.1 基于ITM算法的功率接口

与其他几种接口算法相比，ITM算法凭借其简单的原理、容易实现且高准确性的特性而被广泛采用。目前关于ITM算法的稳定性研究也被充分论证，文献[12, 23-25]从传递函数的角度分析接口系统的稳定性，文献[26-27]通过在动模系统中串联电抗器或在数字侧补偿虚拟电阻的方法提高接口系统的稳定性。理想变压器法根据物理侧跟踪变量的不同，可以分为电压源型和电流源型。图2为基于电压源的理想变压器法原理示意图，其中两侧系统均用戴维南等效电路表示。由图2可知，数字侧和物理侧的电压电流关系如式(1)和式(2)所示。

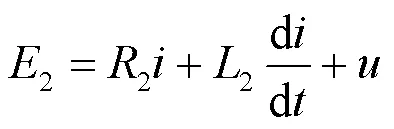
图2 理想变压器法原理示意图

基于电压源型的ITM算法稳定性较差，其接口稳定性条件主要由两侧系统之间的等值阻抗模值和接口系统的延时决定，对于因延时导致的系统不稳定状态，可以通过相位补偿的方式对接口系统进行补偿和修正。

2.2 可编程电源作为接口的实现方式

目前，功率接口采用理想变压器模型算法的数模动模混合仿真实现方式主要有两种：基于线性功率放大器和基于开关型功率放大器的方式[14]。本文采用可编程电源作为混合仿真的功率接口。可编程电源主电路由IGBT整流桥、直流环节和单相MOSFET H桥的逆变器组成，属于电力电子变换器实现方式，也可称为开关型功放。可编程电源在线性度、带宽、动态响应性能方面均优于使用IGBT 作为逆变器的功率接口。同时相对于线性功率放大器，可编程电源不仅具有成本优势，且上升时间低、容量大，可以实现功率的双向流动。因此采用可编程电源作为功率接口实现方式是一种较为理想的选择，本文采用可编程电源作为接口系统的实现方式，其功能相当于一个受控电压源，对参考信号进行追踪放大。整个系统的主要硬件部分如图3所示。

如图3所示，RTDS下发的参考电压信号经过数模动模转换器输出参考模拟电压信号，可编程电源将接收的电压信号放大输出，在动模仿真系统形成波形相同的功率级电压信号波形；动模仿真系统上传的电压和电流信号经过模数转换、比例和滤波等环节，在数字仿真系统形成相同的电压和电流信号波形，这也是接口系统的边界条件。为了适配于动模实验室搭建的动模仿真系统，可编程电源的主要参数如表1所示。

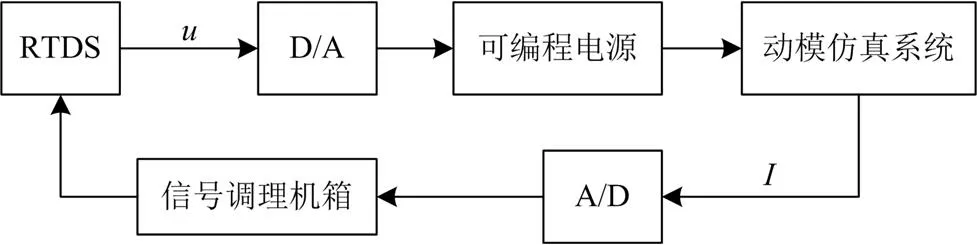
图3 混合仿真系统的信号传输硬件图

表1 可编程电源的主要参数

3 混合仿真系统稳定性分析和准确性分析

即使两个原来独立的数字仿真系统和动模仿真系统稳定，由于接口系统会因固有延时、带宽、噪声和动态特性这些因素导致功率接口输出与输入之间产生幅值误差和相位误差，甚至使得数字仿真系统输出电压瞬时值和电流瞬时值可能不同步，这导致数模动模混合仿真系统也不一定稳定，所以有必要对混合仿真系统进行稳定性分析和准确性分析。

3.1 稳定性分析

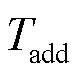
图4 不同延时下系统的奈奎斯特曲线图

3.2 准确性分析与相位补偿

接口系统延时的存在可能会导致混合仿真结果误差增大、准确性降低甚至系统失稳等风险[22]。所以对于下发参考信号和上传信号进行相位补偿是非常有必要的一个环节。对比RTDS下发的A相参考电压信号和可编程电源输出的A相响应信号，可以计算下发通道的相位滞后角度和对应的延时。

如图5所示，通过测量下发参考信号和响应信号之间的相位差，得到响应信号滞后参考信号的角度为3.7º左右，接口系统延时约为205.6 μs。

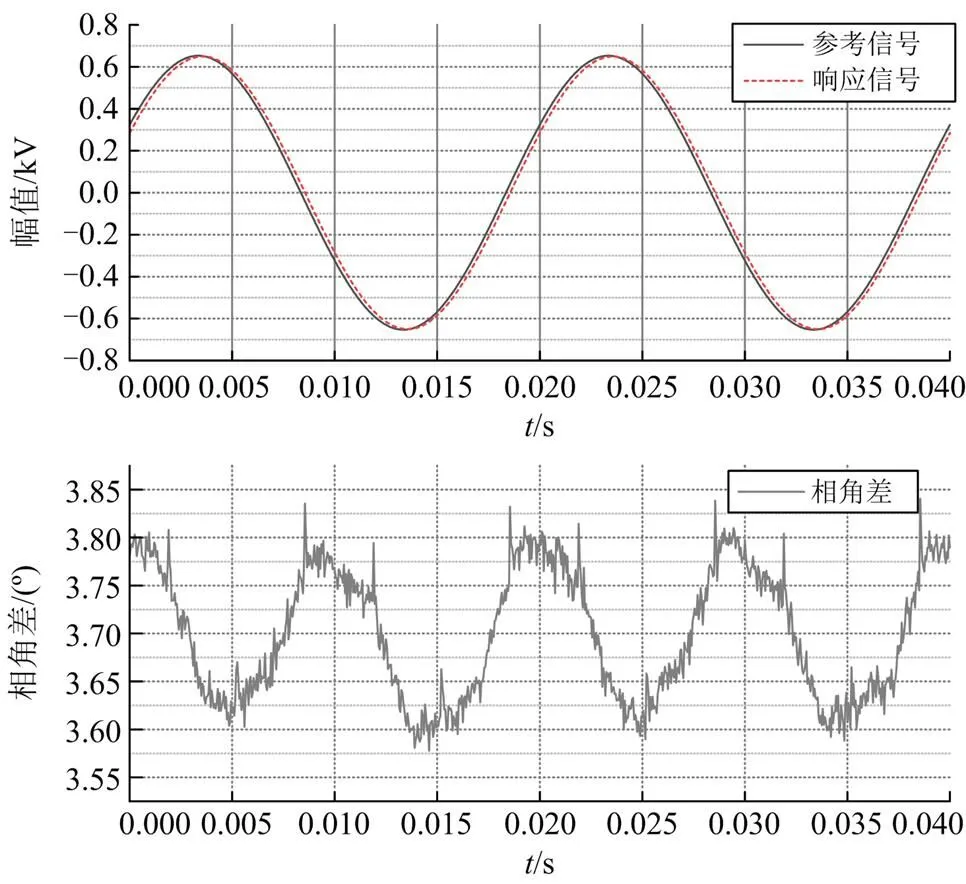
图5 补偿之前参考信号与响应信号对比图

为了减小接口延时带来的影响，本文采用相位超前环节对响应信号进行相位补偿，其频率响应的幅值增益和相位超前表达式分别如式(3)和式(4)所示。

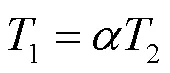
式中，为超前环节最大补偿相位对应的角频率。当时间常数，，增益为1时，设置式(3)中的相位超前环节阶数依次为1、2、3、4，并通过Matlab绘制其伯德图和阶跃响应图分别如图6和图7所示。

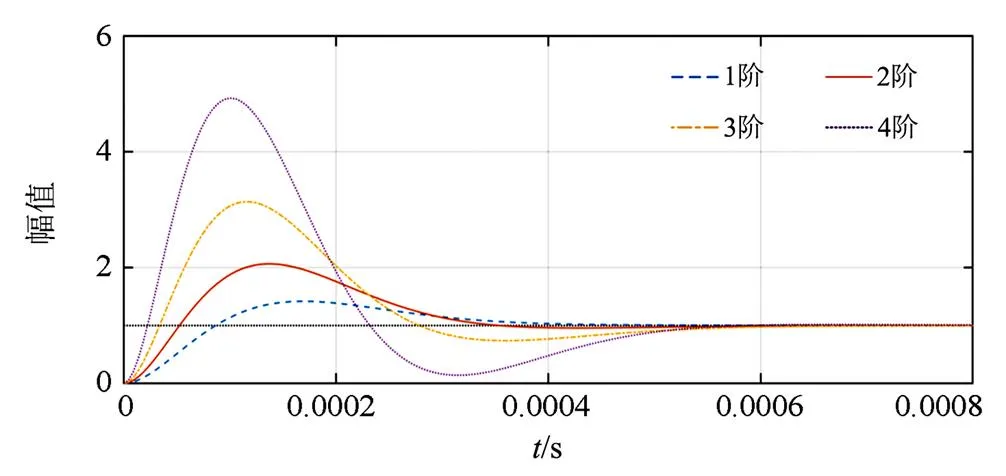
图7 不同阶数下超前环节的单位阶跃响应图

由图6和图7可知，随着超前环节阶数增加，相同频率时超前的角度也相应增加，幅值增益随着阶数增加而增大，当信号中包含高频噪声信号时，可能导致系统不稳定；选择二阶或者三阶相位补偿时，系统的超调量较小，且可以补偿由接口延时导致的相位滞后。

由图8可知，经过二阶超前环节进行相位补偿之后，相位滞后问题得到明显的改善，动态响应良好，参考信号和响应信号波形曲线基本上完全重合。本文所提的通过二阶超前环节补偿接口延时的方法有利于提高整个混合仿真系统的准确性与稳定性。

图8 补偿之后参考信号与响应信号对比图

3.3 可编程电源的输出性能

为验证基于可编程电源的功率接口系统的有效性和功率接口电压的输出特性，使用RTDS搭建正弦阶跃信号发生器，生成基波正弦阶跃信号作为功率接口输入参考信号，验证功率接口的输出电压准确性和电压追踪性能。在RTDS中监测接口输入参考电压，在可编程电源输出的功率接口处监测输出的响应电压信号，得到参考电压的基波正弦阶跃响应如图9所示。

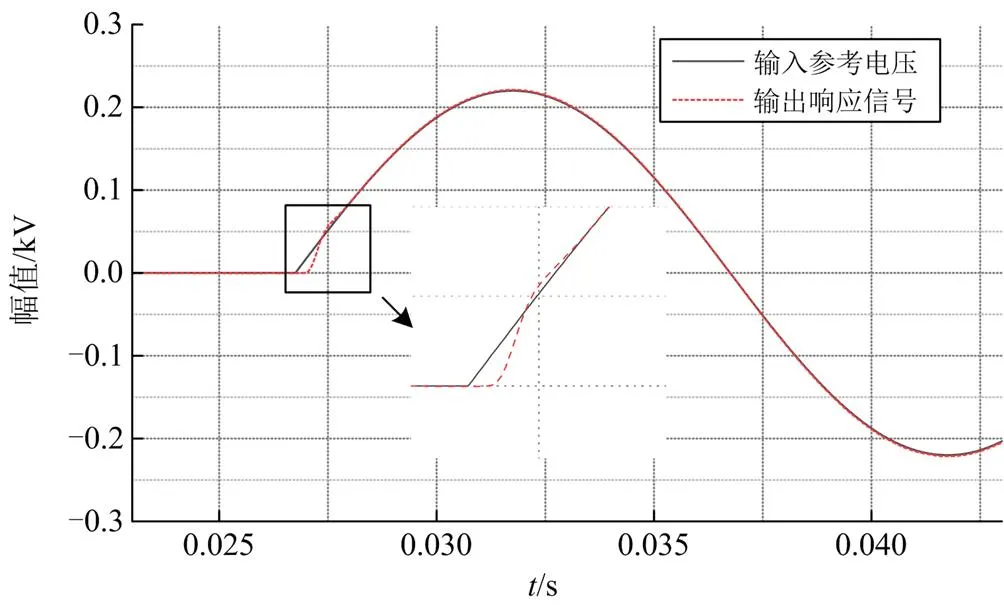
图9 基波正弦阶跃响应图

图10(a)为直流阶跃响应，图10(b)、图10(c)和图10(d)为正弦阶跃信号响应图，参考信号从直流到包含高次谐波的组合波形，经过系统的二阶相位校正之后，下发的参考电压信号与可编程电源输出的响应信号具有相当高的吻合度，二阶相位超前环节校正可以满足接口系统相位补偿的要求。

图10 直流阶跃与组合正弦阶跃响应

4 基于可编程电源的混合仿真系统实验

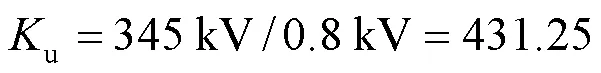
如图11所示，在动模侧线路D11和D12处以及IEEE39节点系统中设置故障点，设置多种故障类型以验证混合仿真系统实验平台的有效性。对比接口系统两侧M点和N点两处A相电流波形，并以两点的电流之差作为误差曲线，如图12所示。

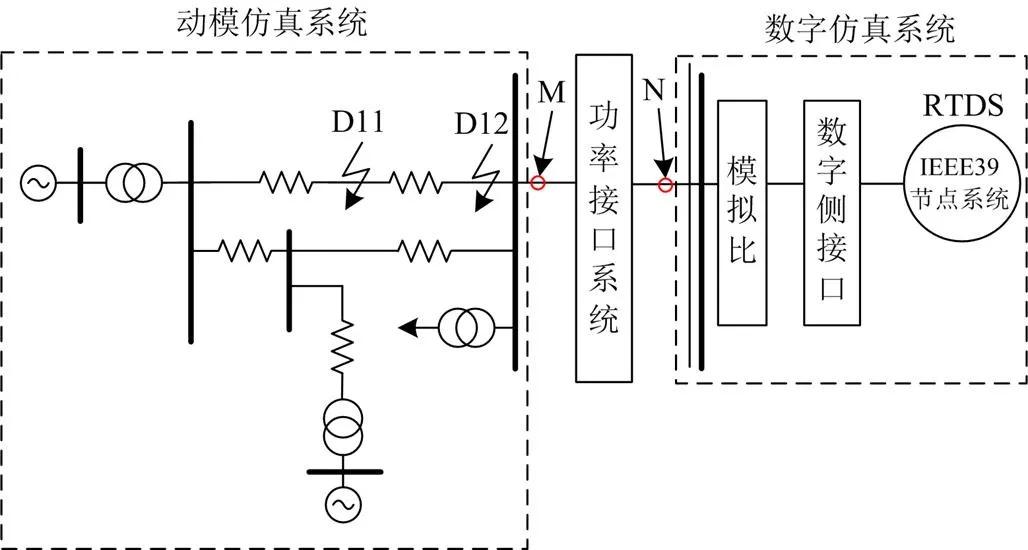
图11 数模动模混合仿真系统示意图

图12 接口系统输入和输出电流波形对比图

从图12可以看出，无论是在稳态期间还是故障期间，M、N两点之间的波形几乎重合，误差很小。证明了该接口系统对于电流信号的追踪性能很好，体现了经过相位补偿后数模动模混合系统良好的稳定性和准确性。

为进一步验证混合仿真结果的准确性，在RTDS中建立动模系统部分的数学模型，与数字仿真系统通过模拟比转换之后直接相连接，实现以纯数字仿真和混合仿真的对比。在相同点设置相同的故障类型，保证仿真条件的一致性，进行纯数字仿真实验，以D12处设置单相(A相)接地故障为例，测量N点的电压与电流波形，结果如图13和图14所示。

从数模动模混合仿真和RTDS纯数字仿真稳态过程波形对比分析可知，无论是电压信号还是电流信号，两者之间的波形基本完全重合。在线路故障时，波形暂态过程中的相位误差不超过50ms，满足实际应用要求。整体而言，两者波形的幅值和相位误差很小，表明数模动模混合仿真的电压跟踪准确性很高。

图13 混合仿真和纯数字仿真N点电流误差图

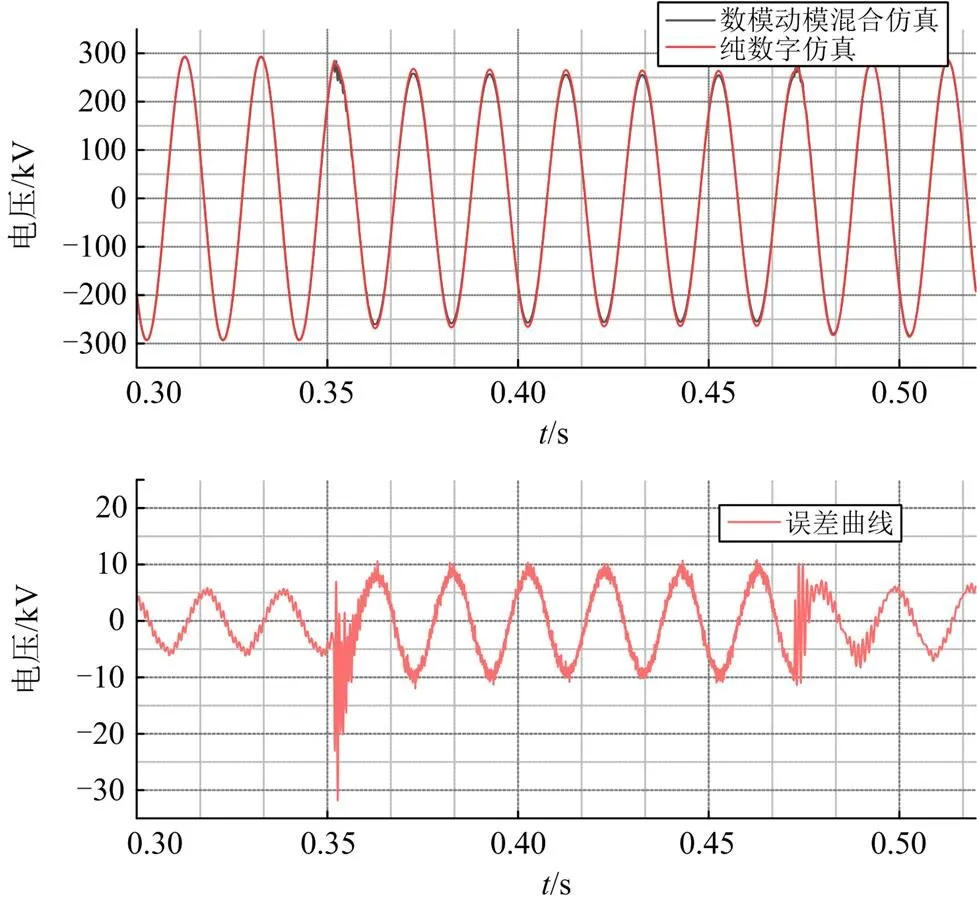
图14 混合仿真和纯数字仿真N点电压误差图

5 结语

为满足越来越高的电力系统实时仿真要求，提出基于可编程电源的数模动模混合仿真系统。本文采用基于可编程电源的ITM电压源法作为接口算法，在动模实验室中搭建动模仿真系统模型，在RTDS中搭建IEEE39节点系统，通过可编程电源连接两者，完成整个800 V/345 kV的数模动模混合仿真系统的设计与搭建。通过对混合仿真系统接口延时和控制策略的研究，完成接口系统上传电流信号和下发电压信号的相位补偿，提升了系统的稳定性和准确性。最后通过纯数字仿真与数模动模混合仿真的波形对比分析可知，无论是稳态过程还是暂态过程，混合仿真都可以满足电力系统仿真要求。但是该系统在宽频特性上需进行调试和完善；另外若采用改进的ITM算法作为接口算法，可以进一步提升系统的稳定性和准确性。

[1] 姚良忠, 吴婧, 王志冰, 等. 未来高压直流电网发展形态分析[J]. 中国电机工程学报, 2014, 34(34): 6007-6020.

YAO Liangzhong, WU Jing, WANG Zhibing, et al. Pattern analysis of future HVDC grid development[J]. Proceedings of the CSEE, 2014, 34(34): 6007-6020.

[2] 赵东元, 胡楠, 傅靖, 等. 提升新能源电力系统灵活性的中国实践及发展路径研究[J]. 电力系统保护与控制, 2020, 48(24): 1-8.

ZHAO Dongyuan, HU Nan, FU Jing, et al. Research on the practice and road map of enhancing the flexibility of a new generation power system in China[J]. Power System Protection and Control, 2020, 48(24): 1-8.

[3] 赵政嘉, 李海波, 赵宇明, 等. 多类型分布式电源接入下的低压交流与直流配电网运行经济性对比[J]. 电力系统保护与控制, 2020, 48(12): 50-61.

ZHAO Zhengjia, LI Haibo, ZHAO Yuming, et al. Operational economic comparison of low voltage AC and DC distribution networks with multi-type distributed generation integration[J]. Power System Protection and Control, 2020, 48(12): 50-61.

[4] PABITRA K G, ABHIK B. Stability enhancement of wind energy integrated hybrid system with the help of static synchronous compensator and symbiosis organisms search algorithm[J]. Protection and Control of Modern Power Systems, 2020, 5(2): 138-150.

[5] 向珉江, 袁通, 苏善诚, 等. 基于5G授时的配网差动保护数据同步方案[J]. 电力系统保护与控制, 2021, 49(8): 8-15.

XIANG Minjiang, YUAN Tong, SU Shancheng, et al. 5G timing base data synchronization scheme for differential protection of distribution networks[J]. Power System Protection and Control, 2021, 49(8): 8-15.

[6] 朱金涛, 辛业春. 柔性高压直流输电仿真技术研究方法综述[J]. 智慧电力, 2021, 49(3): 1-11, 94.

ZHU Jintao, XIN Yechun. Review of research on simulation methods of VSC-HVDC transmission system[J]. Smart Power, 2021, 49(3): 1-11, 94.

[7] 王晨, 吴俊勇, 图尔荪·依明, 等.基于无线通信的配电网单相接地故障定位系统及其动模实验[J]. 电网技术, 2014, 38(8): 2280-2285.

WANG Chen, WU Junyong, TUERSUN Yiming, et al. Wireless communication based single-phase earth fault location in distribution network and its dynamic simulation experiment[J]. Power System Technology, 2014, 38(8): 2280-2285.

[8] SHARMA A, SRIVASTAVA S C, CHAKRABARTI S. Testing and validation of power system dynamic state estimators using real time digital simulator (RTDS)[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2338-2347.

[9] REN W, STEURER M, BALDWIN T L. Improve the stability and the accuracy of power hardware-in-the-loop simulation by selecting appropriate interface algorithms[C] //2007 IEEE/IAS Industrial & Commercial Power Systems Technical Conference, May 6-11, 2007, Edmonton, AB, Canada.

[10] 曾杰, 冷凤, 陈晓科, 等. 现代电力系统大功率数模混合实时仿真实现[J]. 电力系统自动化, 2017, 41(8): 166-171, 178.

ZENG Jie, LENG Feng, CHEN Xiaoke, et al. Implementation of high power digital-analog hybrid real-time simulation for modern power systems[J]. Automation of Electric Power Systems, 2017, 41(8): 166-171, 178.

[11] 胡涛, 朱艺颖, 张星, 等. 全数字实时仿真装置与物理仿真装置的功率连接技术[J]. 电网技术, 2010, 34(1): 51-55.

HU Tao, ZHU Yiying, ZHANG Xing, et al. Power connection technology for full-digital real-time simulator and analogue simulator[J]. Power System Technology, 2010, 34(1): 51-55.

[12] BOKAL M, PAPIC I, BLAZIC B. Stabilization of hardware-in-the-loop ideal transformer model interfacing algorithm by using spectrum assignment[J]. IEEE Transactions on Power Delivery, 2019, 34(5): 1865-1873.

[13] 李俊林, 毛承雄, 王丹, 等. 电力系统数字物理混合仿真相位校正方案[J]. 水电能源科学, 2017, 35(3): 190-194.

LI Junlin, MAO Chengxiong, WANG Dan, et al. Phase correction scheme used in digital and physical hybrid simulation of power systems[J]. Water Resources and Power, 2017, 35(3): 190-194.

[14] 张硕廷. 电力系统数字物理混合仿真系统研制[D]. 武汉: 华中科技大学, 2014.

ZHANG Shuoting. Development of power system digital and physical hybrid simulation system[D]. Wuhan: Huazhong University of Science and Technology, 2014.

[15] 陈磊, 闵勇, 叶骏, 等. 数字物理混合仿真系统的建模及理论分析(一)系统结构与模型[J]. 电力系统自动化, 2009, 33(23): 9-13.

CHEN Lei, MIN Yong, YE Jun, et al. Modeling and theoretical analysis of hardware-in-the-loop simulation (part one) structure and model[J]. Automation of Electric Power Systems, 2009, 33(23): 9-13.

[16]李岩军, 陈争光, 刘文华, 等. MMC-HVDC的数模混合仿真系统设计方案[J]. 电力系统及其自动化学报, 2019, 31(9): 58-65.

LI Yanjun, CHEN Zhengguang, LIU Wenhua, et al. Design scheme for digital-analog hybrid simulation system of MMC-HVDC[J]. Proceedings of the CSU-EPSA, 2019, 31(9): 58-65.

[17] PARMA G G, DINAVAHI V. Real-time digital hardware simulation of power electronics and drives[J]. IEEE Transactions on Power Delivery, 2007, 22(2): 1235-1246.

[18]蔡玲珑. 数模混合实时仿真系统应用及直流分量消除[D]. 武汉: 华中科技大学, 2016.

CAI Linglong. Application of real time digital-analog hybrid simulation system and its DC component elimination[D]. Wuhan: Huazhong University of Science and Technology, 2016.

[19]梁志成, 马献东, 王力科, 等. 实时数字仿真器RTDS及其应用[J]. 电力系统自动化, 1997, 21(10): 61-64.

LIANG Zhicheng, MA Xiandong, WANG Like, et al. Real time digital simulator RTDS and its application[J]. Automation of Electric Power Systems, 1997, 21(10): 61-64.

[20] 夏天华, 马骏超, 黄弘扬, 等. 基于RTDS硬件在环测试的SVG控制器参数辨识[J]. 电力系统保护与控制, 2020, 48(13): 110-116.

XIA Tianhua, MA Junchao, HUANG Hongyang, et al. Parameter identification for SVG controller based on RTDS hardware-in-the-loop test[J]. Power System Protection and Control, 2020, 48(13): 110-116.

[21]高源, 陈允平, 刘会金. 电力系统物理与数字联合实时仿真[J]. 电网技术, 2005, 29(12): 77-80.

GAO Yuan, CHEN Yunping, LIU Huijin. Joint physico- digital real-time simulation of power system[J]. Power System Technology, 2005, 29(12): 77-80.

[22] RON B. Operational range of several interface algorithms for different power hardware-in-the-loop setups[J]. Energies, 2017, 10(12).

[23] LENTIJO S, D 'ARCO S, MONTI A. Comparing the dynamic performances of power hardware-in-the-loop interfaces[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1195-1207.

[24] AYASUN S, FISCHL R, VALLIEU S, et al. Modeling and stability analysis of a simulation-stimulation interface for hardware-in-the-loop applications[J]. Simulation Modelling Practice & Theory, 2007, 15(6): 734-746.

[25]许中, 尹晨旭, 刘邦, 等. 功率硬件在环仿真稳定性分析及功率接口研究[J]. 电力自动化设备, 2016, 36(11): 165-170.

XU Zhong, YIN Chenxu, LIU Bang, et al. Analysis of PHIL simulation stability and implementation of power interface[J]. Electric Power Automation Equipment, 2016, 36(11): 165-170.

[26]乐健, 张好, 李星锐, 等. 基于虚拟电阻补偿的柔性直流输电数模混合仿真系统的功率接口建模方法[J]. 中国电机工程学报, 2018, 38(18): 5352-5360.

LE Jian, ZHANG Hao, LI Xingrui, et al. A power interface modeling method of the digital-physical hybrid simulation system of MMC-HVDC system based on virtual resistance compensation[J]. Proceedings of the CSEE, 2018, 38(18): 5352-5360.

[27] HONG M, HORIE S, MIURA Y, et al. A method to stabilize a power hardware-in-the-loop simulation of inductor coupled system[C] // Proceeding of International Conference on Power System Transients, June 3-6, 2009, Kyoto, Japan: 1-7.

[28] 叶骏, 闵勇, 闵睿, 等. 基于时序分析的数字物理混合仿真技术(三)稳定性分析[J]. 电力系统自动化, 2012, 36(15): 14-18.

YE Jun, MIN Yong, MIN Rui, et al. Hardware-in-the- loop simulation technology based part three stability analysis (part three) stability analysis[J]. Automation of Electric Power Systems, 2012, 36(15): 14-18.

A digital and dynamic analog hybrid simulation system based on programmable power

LI Zhenxing1, 2, LIN Longjian1, LENG Feng3, WENG Hanli1, LI Fei1

(1. Hubei Provincial Key Laboratory for Operation and Control of Cascaded Hydropower Station, China Three Gorges University,Yichang 443002, China; 2. College of Electricity & New Energy, China Three Gorges University, Yichang 443002, China;3. State Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

To meet the development needs of modern power system simulation, a digital and dynamic analog hybrid real-time simulation system based on programmable power supply is proposed. A dynamic simulation laboratory is used to build the dynamic simulation subsystem model, and the New England 39-node system is built in RTDS as the digital simulation subsystem. Combined with an interface subsystem using the ideal transformer model as the power interface method, an 800 V/345 kV digital and dynamic analog hybrid real-time simulation system experimental platform is formed. Based on the study of the influence of system delay at both ends of hybrid simulation interface on system stability and accuracy, a second-order phase advance link is proposed to compensate for the interface delay of the transmitting channel and the uploading channel, and a power interface subsystem is proposed to improve system stability and accuracy. Through an experiment of the dynamic analog and hybrid simulation system, and by comparison with pure digital simulation, the effectiveness of the hybrid simulation system is further verified.

digital analog hybrid real-time simulation; interface algorithm of ideal transformer model; phase compensation; pure digital simulation

10.19783/j.cnki.pspc.211672

2021-12-08

李振兴(1977—)，男，博士，副教授，主要从事电力系统保护与控制研究工作。E-mail: lzx2007001@163.com

This work is supported by the National Natural Science Foundation of China (No. 52077120).

国家自然科学基金项目资助(52077120)

(编辑 魏小丽)