基于RBF神经网络的电压外环滑模控制的Vienna整流器

杨旭红，陈 阳，贾 巍，方剑峰，罗 新，高子轩

基于RBF神经网络的电压外环滑模控制的Vienna整流器

杨旭红1，陈 阳1，贾 巍2，方剑峰1，罗 新1，高子轩1

(1.上海电力大学自动化工程学院，上海 200090；2.上海太阳能工程技术研究中心，上海 200241)

以Vienna整流器为研究对象，针对其传统电压外环滑模变结构控制不变性和对系统参数扰动敏感的问题，分析了以逼近率为基础的滑模变结构控制算法，提出了一种基于RBF神经网络的自适应电压外环滑模控制算法。该控制算法通过将RBF神经网络与滑模控制算法有效结合，同时将中点电位平衡控制加入到RBF神经网络自适应电压外环滑模控制算法的设计中，使用RBF神经网络对电压外环非线性系统进行自适应逼近，能够有效降低切换增益，削弱抖振，增强系统的抗干扰能力。最后，通过仿真分析与实验测试验证所提控制算法的有效性。将所提出的控制算法与传统滑模控制算法、PI控制算法进行比较，结果表明采用这种电压外环控制算法能够对直流输出电压目标值进行快速跟踪，平衡中点电位，改善了系统的动静态性能，提升了其抗干扰能力。

Vienna整流器；电压外环；滑模控制；趋近率；RBF神经网络

0 引言

Vienna整流器以其独特的优势受到越来越多的关注和应用。由于Vienna整流器的单向潮流特性，主要用于中、大功率场合的单向整流或两级变流器的前级升压整流模块。目前，典型的应用场合包括航空电源、直流不间断电源(UPS)、直流充电桩等[1-3]。

目前，对Vienna整流器的研究主要集中在建立与分析数学模型、优化脉冲宽度调制技术和优化设计环路控制策略三方面。文献[1-2]研究了Vienna整流器一些典型的数学模型；文献[3-9]对其调制算法进行了整体优化设计。对于Vienna整流器的外环电压多采用PI控制，但系统存在由输出电压误差线性求和造成的输出电压超调大以及由积分环节饱和引起的动态响应速度慢等缺点，因此有必要从电压外环着手进行控制系统的优化设计。文献[10]使用ADRC(自抗扰控制)来设计电压外环控制器，在一定程度上解决了输出电压快速性与超调之间的矛盾；文献[11-12]采用滑模控制设计电压外环控制器，可以来解决Vienna整流器非线性系统控制问题，输出电压快速性与超调之间的矛盾也得到了进一步解决。文献[13]提出将模糊算法应用到滑模控制器中，直流侧输出的电压性能得到进一步优化，电流的THD也得到了优化。以上电压外环控制策略存在的共同缺点是都要另外用PI控制器来进行中点电位的控制[14-15]。

本文将RBF神经网络[16-17]与Vienna整流器的电压环路滑模控制器相结合，设计出了基于RBF神经网络的电压环自适应滑模控制器。RBF神经网络的收敛速率快，结构简单，具有最佳近似性并非常适用于实时的在线控制。将RBF神经网络和滑模控制结合起来，利用RBF神经网络逼近电压外环滑模的非线性函数，有效减小启动器增益和抖动。同时，将中点电位平衡控制与RBF神经网络自适应滑模控制一起加入，形成了新的电压外环控制算法，即RBF神经网络自适应控制算法，不仅节省了资源，而且改善了控制性能。最后，利用Simulink仿真和实验验证与其他控制器进行了对比分析，结果表明新型控制算法能够对直流输出电压目标值进行快速跟踪，平衡中点电位，提高了系统的动态性和鲁棒性，具有更大的优势。

1 dq旋转坐标系下Vienna整流器的数学模型

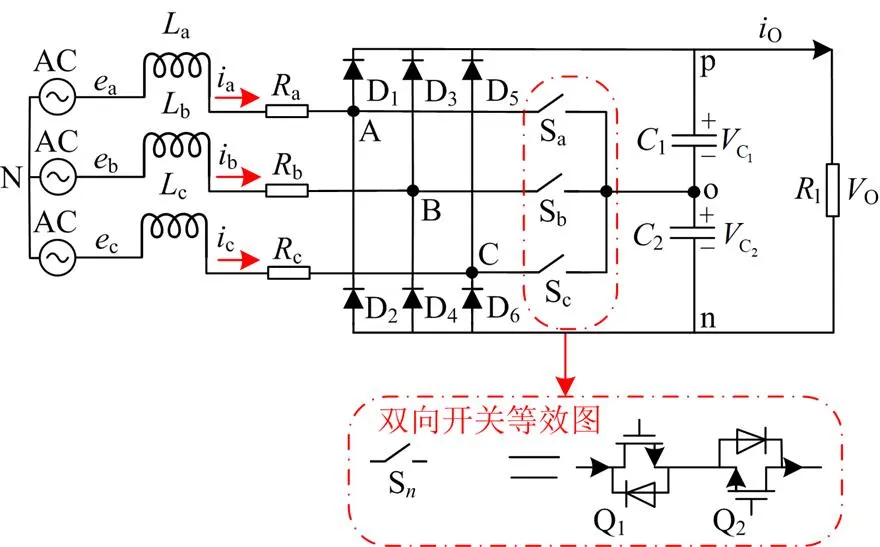
图1 Vienna整流器拓扑结构图

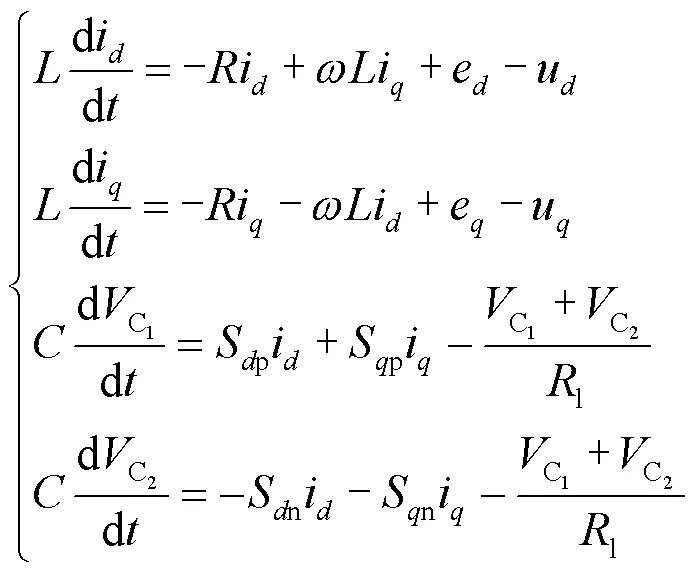
式中：

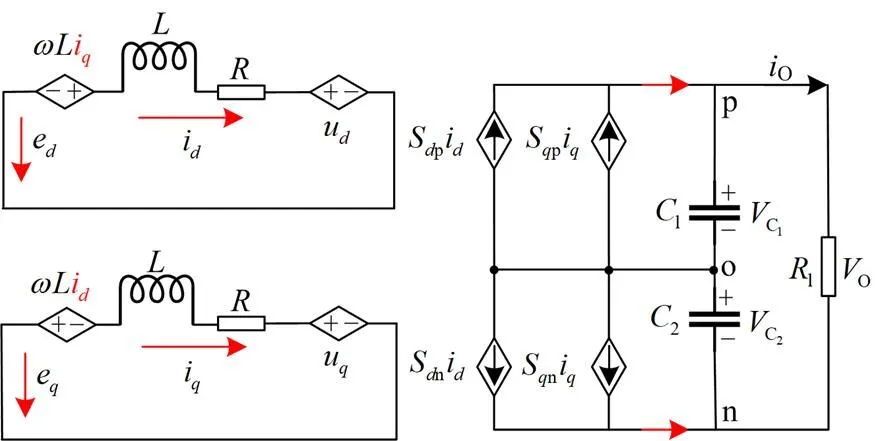
2 电流内环反馈线性化控制器的设计

对系统输出求导，可得

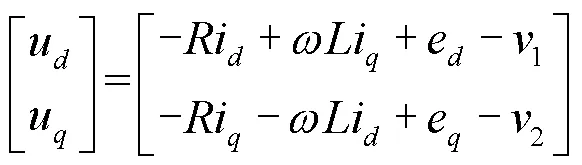
3 电压环控制器的设计

3.1 电压控制环滑模控制器的设计

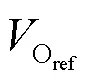
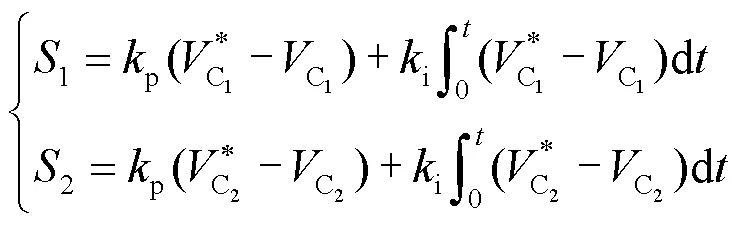
为了减弱滑模变结构的抖动，设计趋近率形式如式(8)。

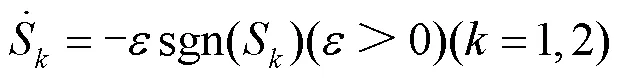
对式(7)求导，可得

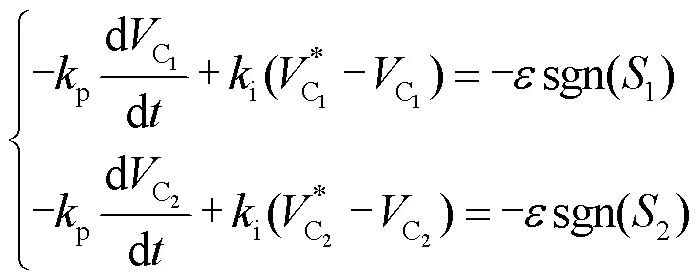
对式(9)化简可得

控制系统满足式(11)。

求解式(11)可得

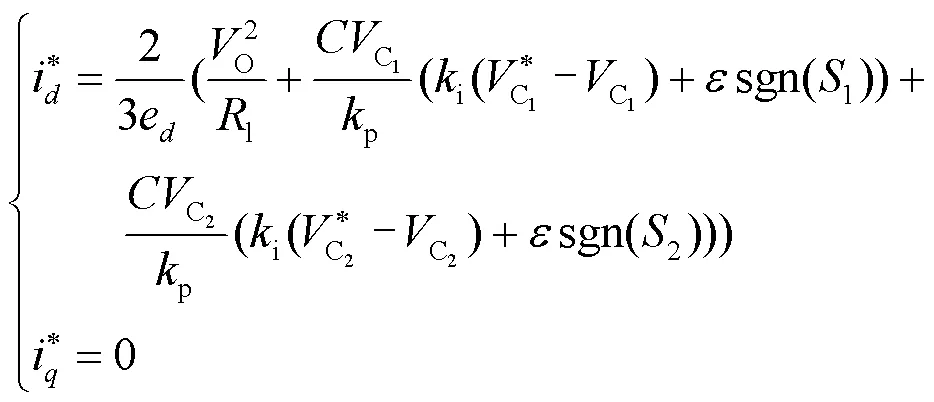
3.2 滑模特性分析

定理1：

由式(13)可得该控制系统满足存在性和可达性的条件，定理1得证。

4 基于RBF自适应神经网络电压外环控制器的设计与分析

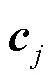
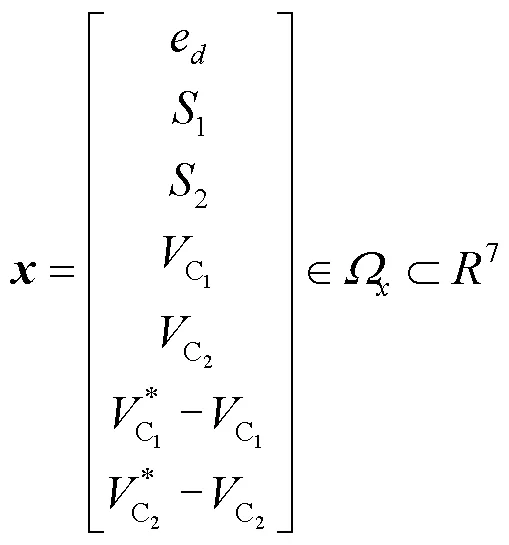
取性能指标函数为

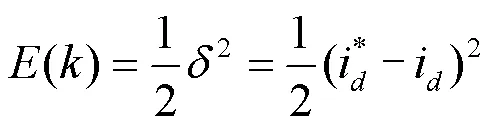
采用最速下降法对神经网络进行学习和在线调整，隐含层的基函数通常选择如式(16)所示的高斯基函数。

选用Matlab仿真软件对所设计网络进行训练。使用同一样本对隐含层神经元个数从6到16的网络进行训练并比较结果，如表1所示。

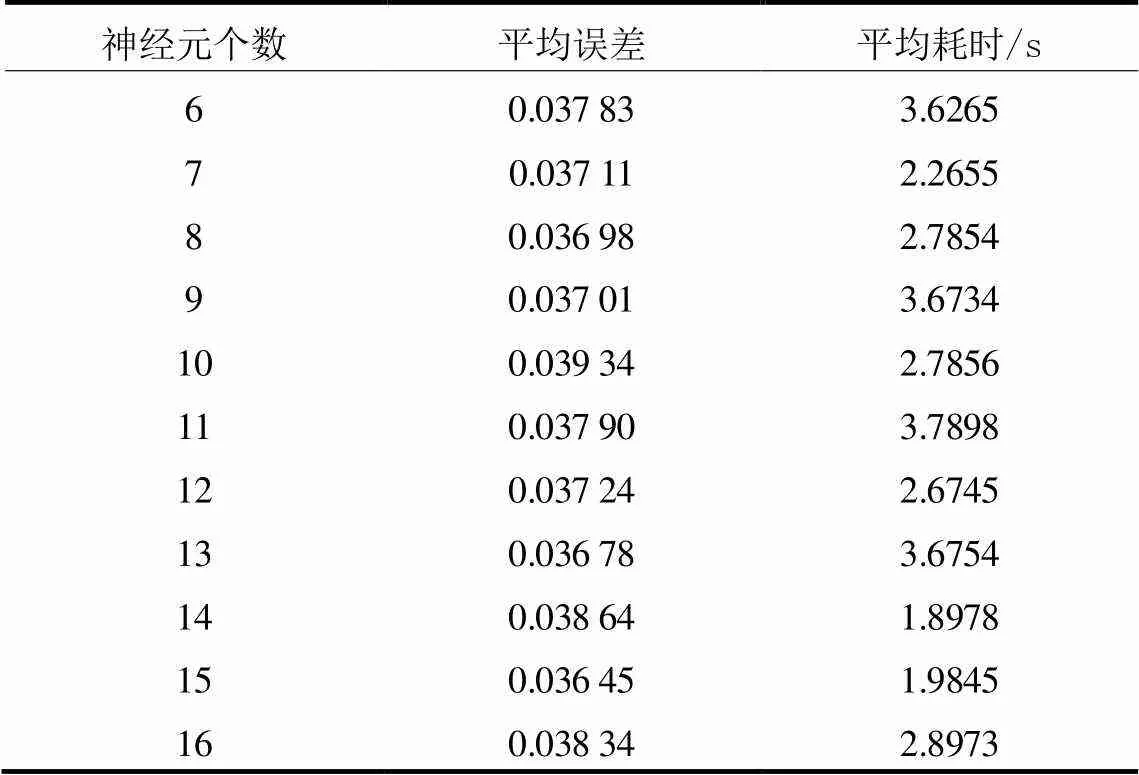
表1 不同数量隐含层神经元节点的神经网络测试结果

根据表1实验效果，的取值为15。

图3 神经网络模型结构图

由图3可知，其输出表达式为

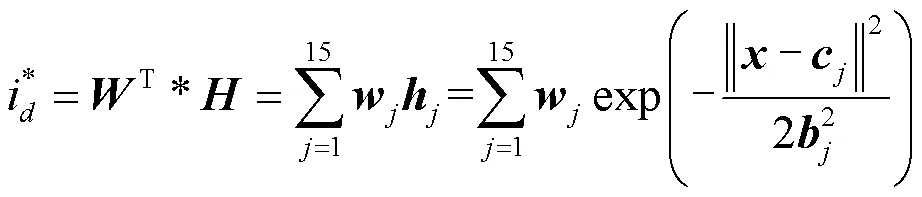
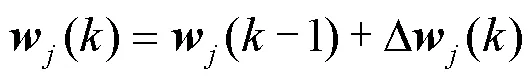
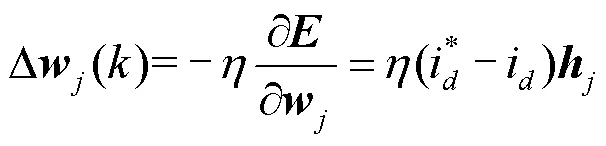
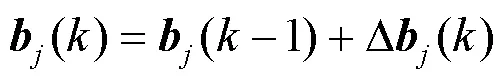
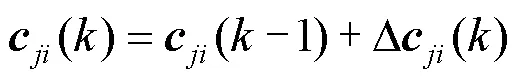
图3所示网络的理想输出值记为

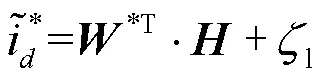
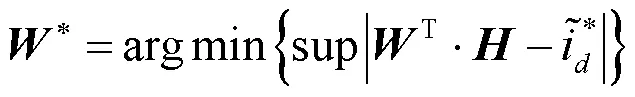
式(27)是连接权值的鲁棒更新算法。

在设计Lyapunov函数时考虑包含滑模面与鲁棒自适应率，具体表达式为

对式(28)求导得

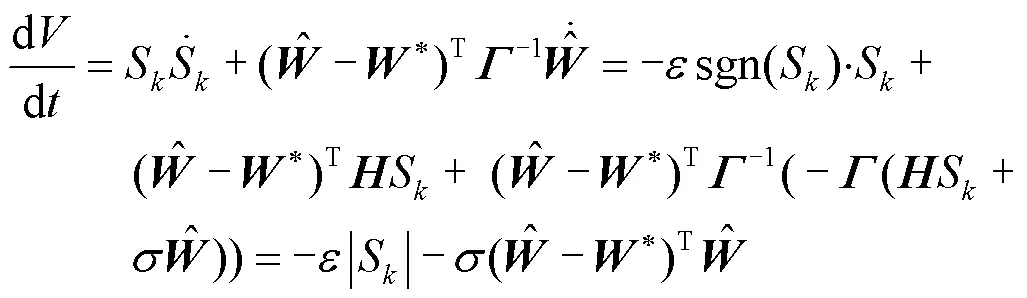
式中：

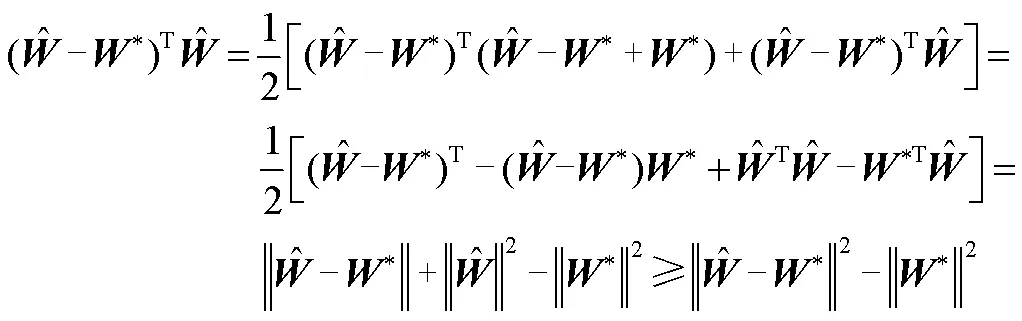
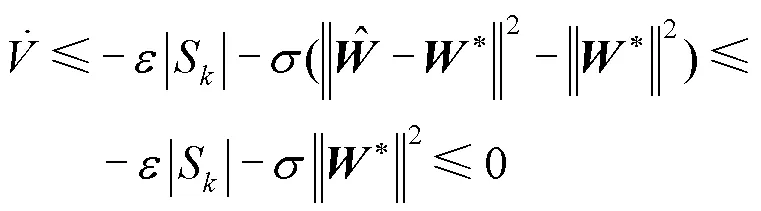
所以该控制系统满足存在性和可达性的条件[26]。

因此，基于RBF神经网络自适应控制器的设计结构如图4所示。

图4 基于RBF神经网络自适应控制器

Fig. 4 Adaptive controller based on improved RBF neural network

综上所述，得到如图5所示的Vienna整流器控制原理框图。

图5 三相Vienna整流器控制框图

5 Simulink仿真验证

通过表2(除控制器部分)里的仿真参数来验证控制算法的有效性。

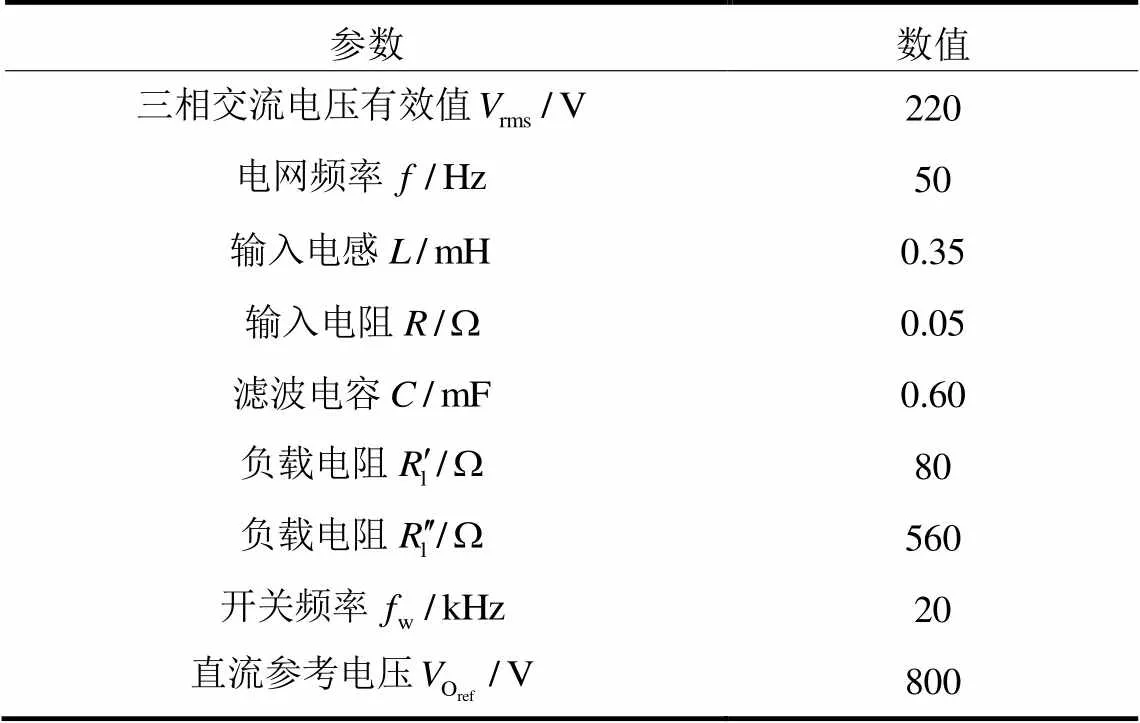
表2 仿真参数

5.1 硬件参数设计

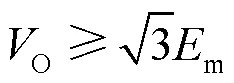
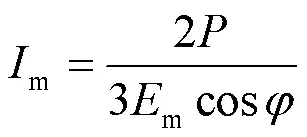
则式(32)可写为

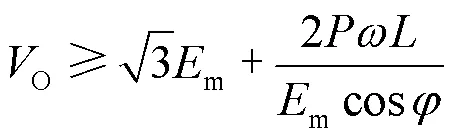
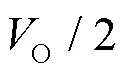
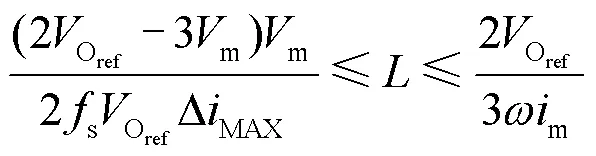
综合考虑成本、装置体积以及性能指标，本文选取的电感量为3.5 mH。

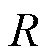
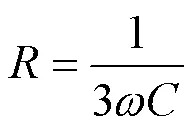
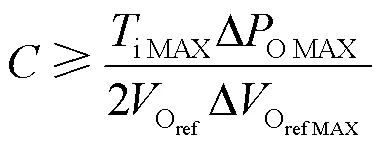
5.2 改进的控制算法

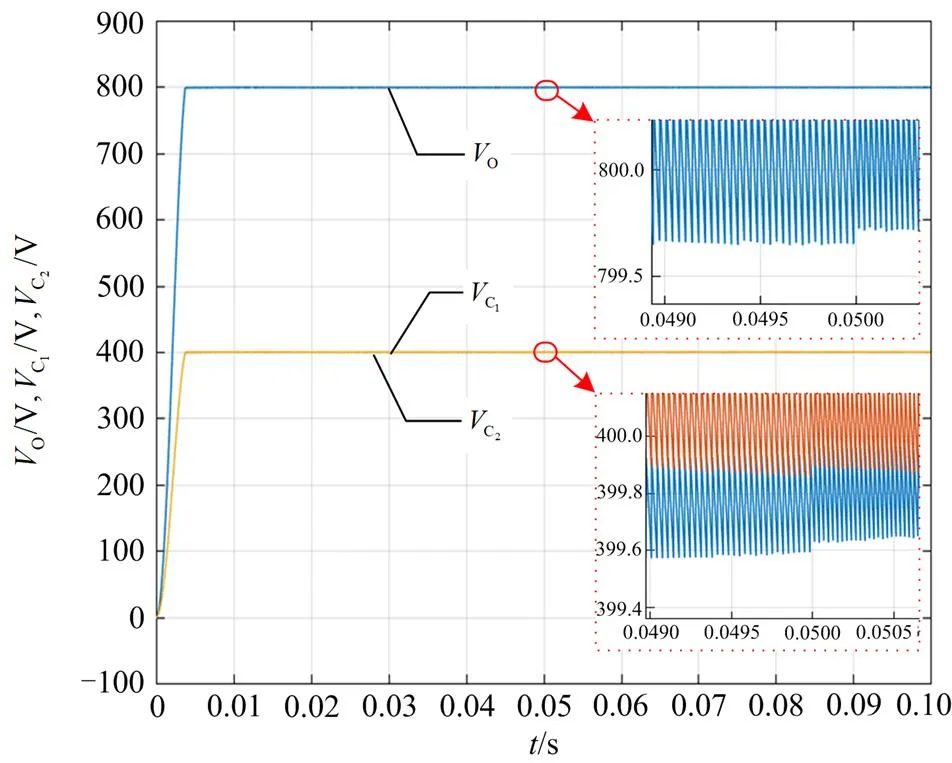
图6 直流侧输出端电压波形

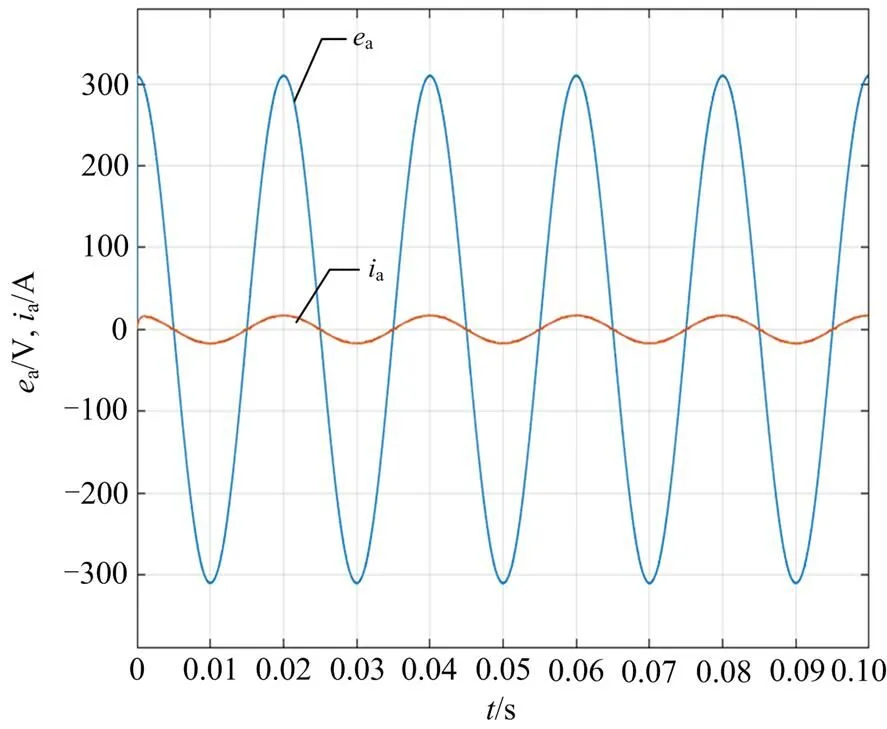
图7 交流输入端a相电压、电流波形

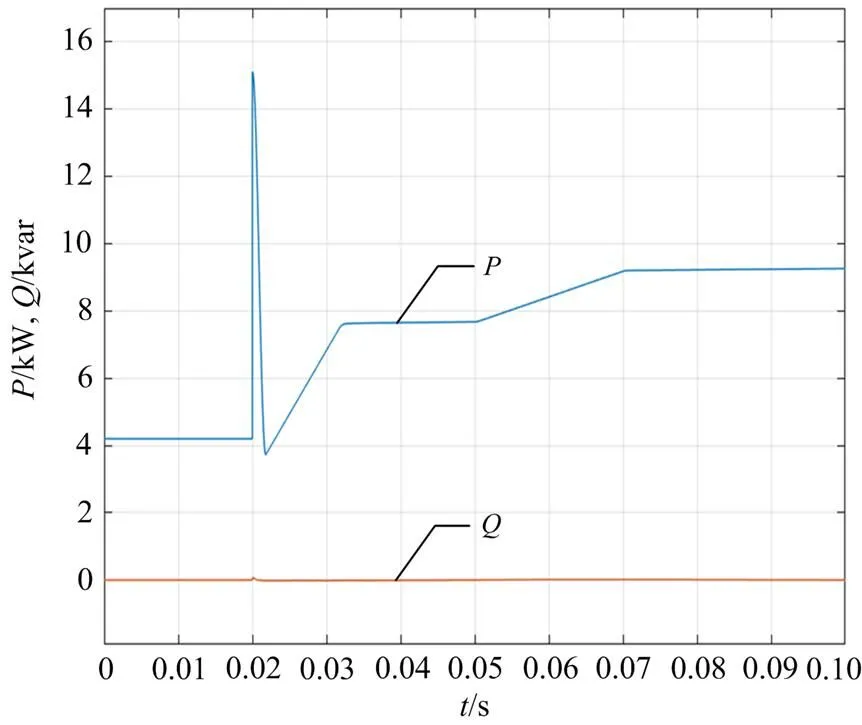
图8 有功功率、无功功率波形

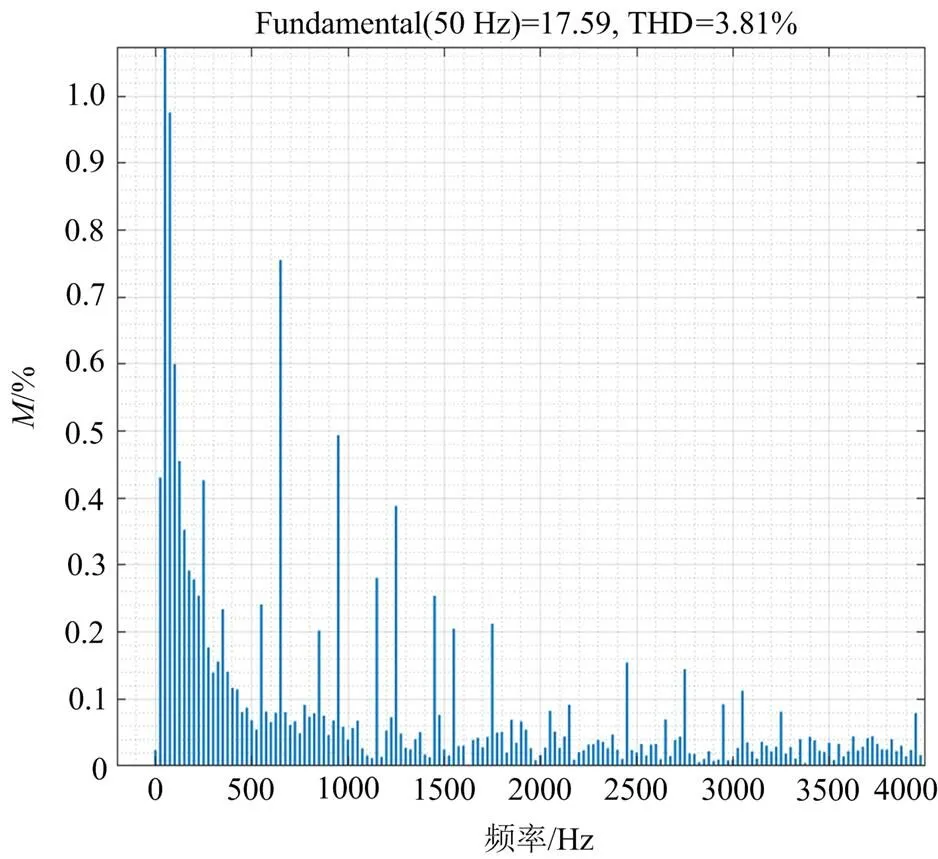
图9 负载突变时a相电流频谱

图10 负载稳定后a相电流频谱

5.3 硬件参数变化控制方法误差分析

图11 负载突变时两种控制算法动态仿真分析

5.4 三种控制算法仿真结果对比

从表3可以看出，基于双闭环PI控制算法直流电压输出曲线的超调量和调节时间最大，分别达到46.625%和0.033 s(一个半电网周期)，同时输入电流的THD也比较大，中点平衡特性比较差。当运用滑模控制对电压外环控制算法进行改进时，系统直流输出曲线的超调量降低了36%，但是系统的响应速度降低了，上升时间从0.003 s增加到0.009 s(半个电网周期)，此时调节时间也变小了；输入端电流的THD也减小了，中点电位平衡能力得到提升，系统的有功功率变化比较稳定，无功功率基本稳定在零，不会出现负值，传统的电压外环滑模控制算法对系统控制性能的提升起到了较大的作用。

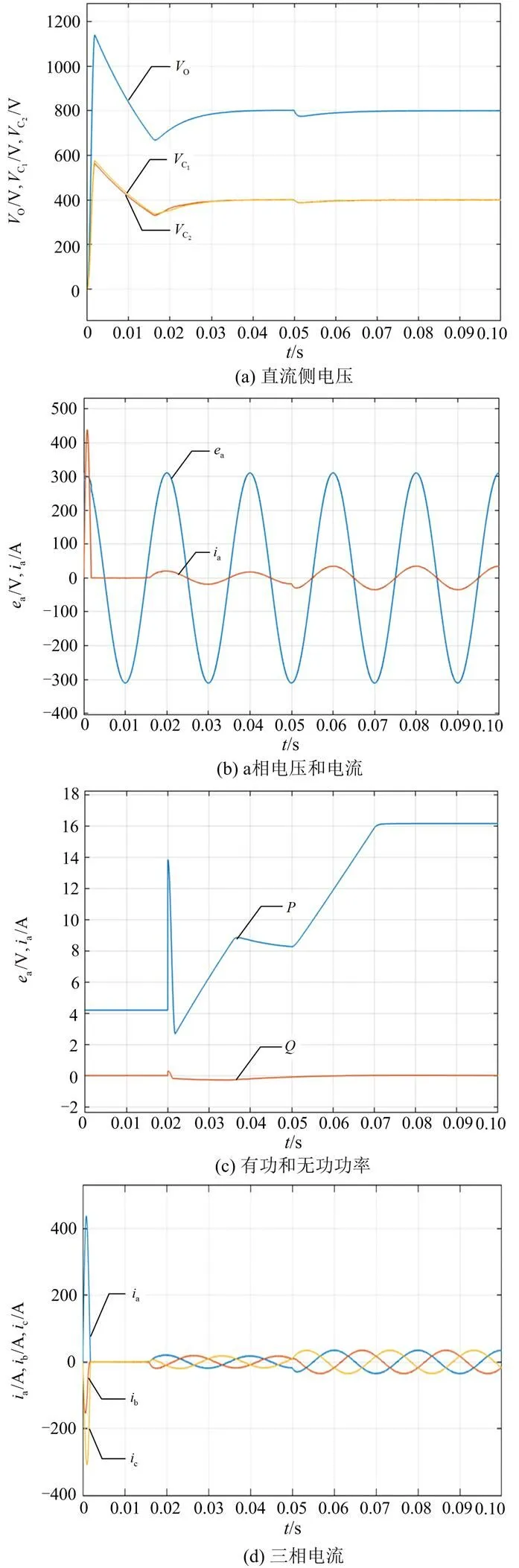
图12 双闭环PI控制

图13 新控制算法

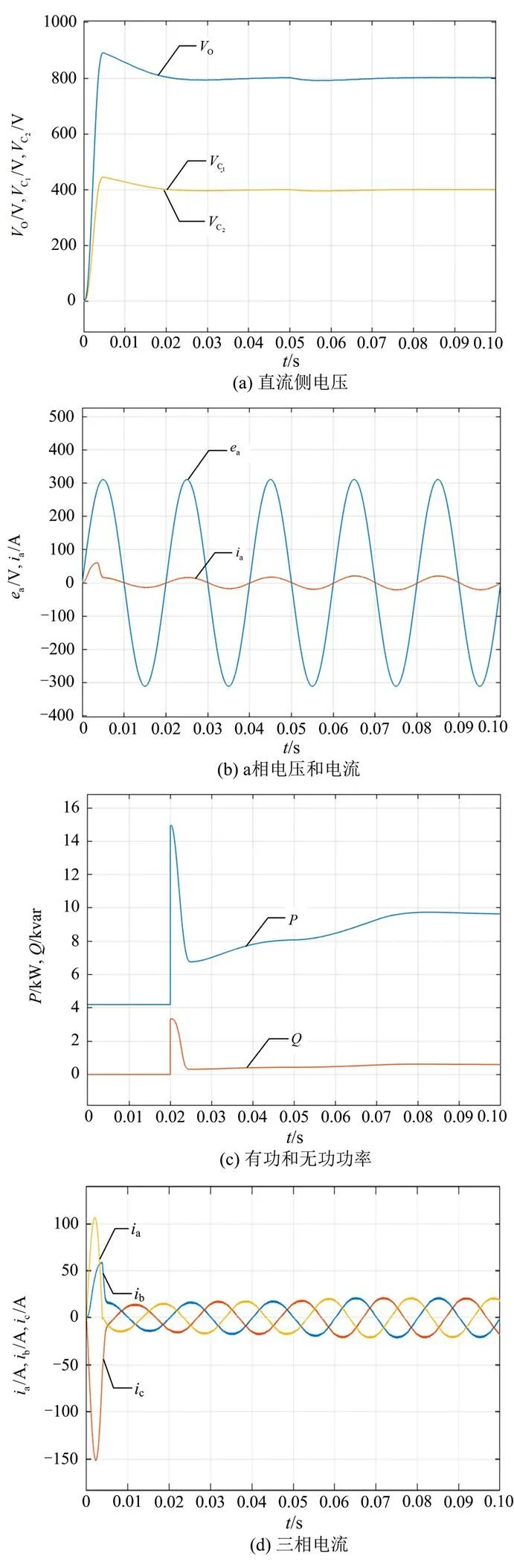
图14 反馈线性化+滑模控制

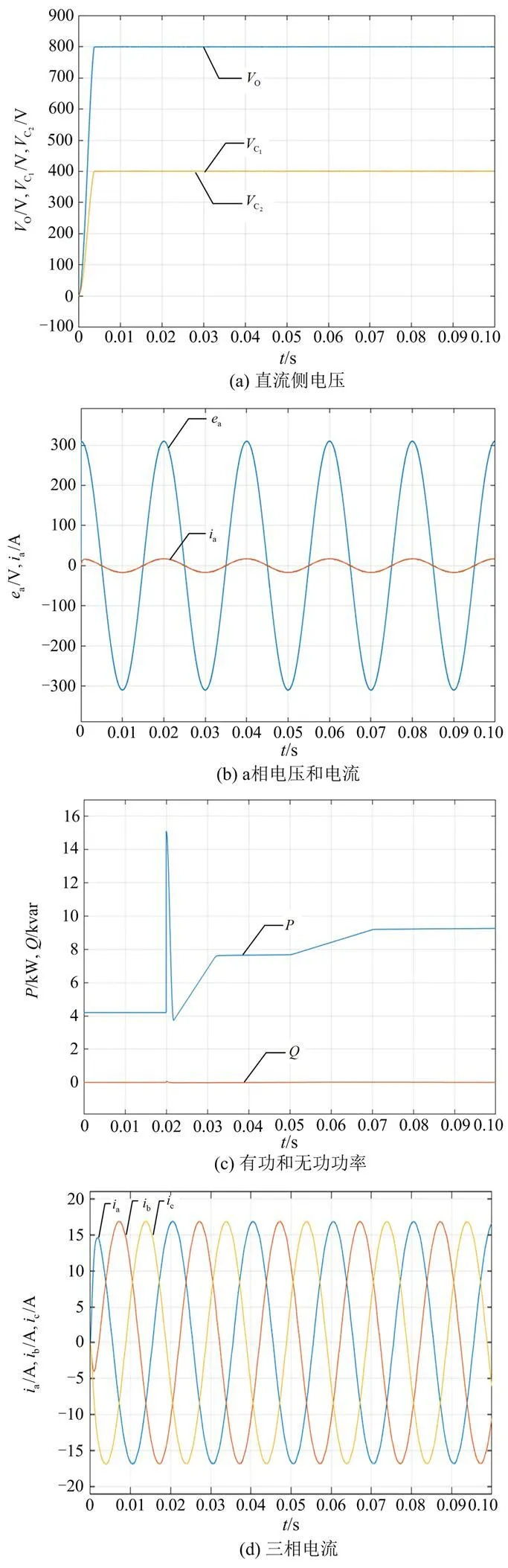
图15 新控制算法

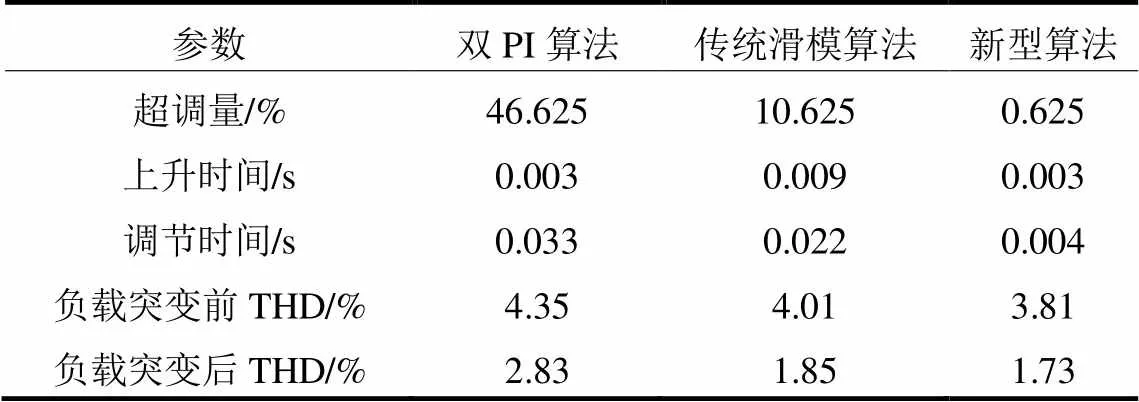
表3 控制性能参数对比

运用RBF神经网络对传统的电压外环滑模控制进行改进，优化成一种新型的外环电压控制算法。超调量、上升时间、调节时间等动静态性能都得到了进一步的提升，运用这种电压外环控制算法对电压外环进行控制时，直流输出曲线的超调量变为0.625%，上升时间和调节时间也得到了进一步的减小，分别变为0.003 s和0.004 s；输入电流THD在负载启动后和稳定时分别为3.81%和1.73%，电流畸变小了。

6 实验验证

为验证本文所提出的改进滑模电压外环控制策略的有效性，搭建了如图16所示的Vienna整流器实验平台。实验参数依然如表2所示。控制器采用德州仪器TMS320F2812，数字信号处理器可通过RT-LAB的模拟量输入输出通道与下位机通信实现闭环控制。

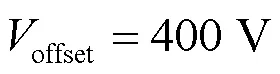
图16 Vienna整流器实验平台

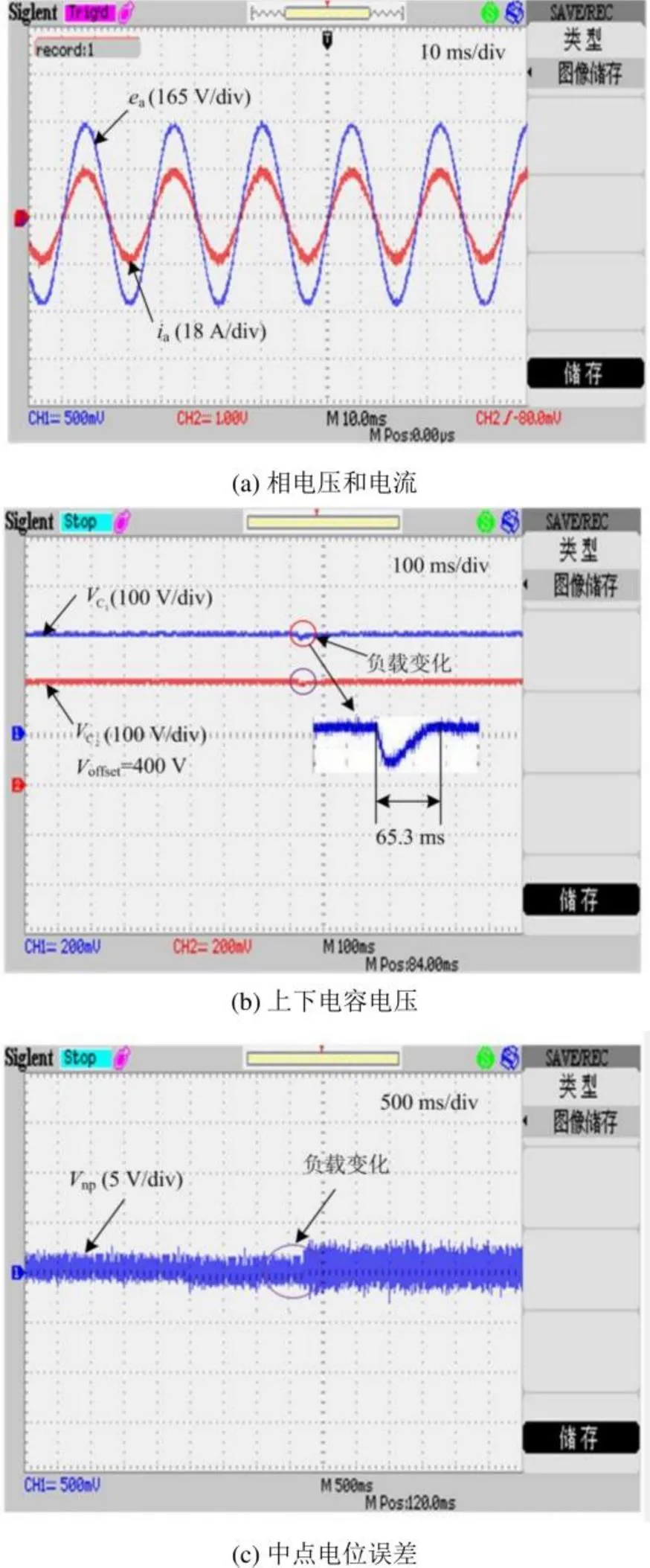
图17 反馈线性化+滑模控制

图18 新控制算法

表4 不同控制算法执行时间对比

7 结论

本文提出了一种新型基于反馈线性化电流内环和基于RBF神经网络的电压外环三相三电平Vienna整流器混合控制策略。与传统的反馈线性化加滑模混合控制相比，该控制算法综合考虑了直流电压、中点电位平衡和输入侧电流3个控制目标，使系统的静动态性能得到了进一步提升。用Simulink搭建仿真模型，与双PI控制和传统的混合控制进行性能对比，并且经过实验测试验证，结果表明：采用新型混合控制算法，在系统启动和负载突变的时候既提升了系统响应速度，又使系统的抗干扰能力得到进一步提升，同时满足系统控制性能要求，保证交流侧输入电流为正弦，变小；输出端得到电压可控且纹波小的直流电压，中点电位达到平衡。

[1] THANGAVELU T, SHANMUGAM P, RAJ K. Modelling and control of VIENNA rectifier a single phase approach[J]. IET Power Electronics, 2015, 8(12): 2471-2482.

[2] MA HUI, XIE, YUNXIANG, SUN, BIAOGUANG, et al. Modeling and direct power control method of Vienna rectifiers using the sliding mode control approach[J]. Journal of power electronics: a publications of the Korean Institute of Power Electronics, 2015, 15(1): 190-201.

[3] ZHU Wenjie, CHEN Changsong, DUAN Shanxu, et al. A carrier-based discontinuous PWM method with varying clamped area for Vienna rectifier[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7177-7188.

[4] ZHANG Li, ZHAO Rui, JU Ping, et al. A modified DPWM with neutral point voltage balance capability for three-phase Vienna rectifiers[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 263-273.

[5] HANG Lijun, ZHANG Ming, LI Bin, et al. Space vector modulation strategy for VIENNA rectifier and load unbalanced ability[J]. IET Power Electronics, 2013, 6(7): 1399-1405.

[6] 周左, 汪洋, 李正明. 基于占空比控制的Vienna整流器模型预测控制策略[J]. 电力系统保护与控制, 2021, 49(10): 162-169.

ZHOU Zuo, WANG Yang, LI Zhengming. Model predictive control strategy of a Vienna rectifier based on duty cycle control[J]. Power System Protection and Control, 2021, 49(10): 162-169.

[7] XING Xiangyang, LI Xiaoyan, QIN Changwei, et al. Two-layer pulsewidth modulation strategy for common- mode voltage and current harmonic distortion reduction in Vienna rectifier[J]. IEEE Transactions on Industrial Electronics, 2020, 67(9): 7470-7483.

[8] FADAEIAN T, GHOLAMIAN S A, GHOREISHY H. A novel discontinuous pulse width modulation strategy based on circuit-level decoupling concept for Vienna rectifier[J]. Revue Roumaine des Sciences Techniques. Serie Electrotechnique et Energetique, 2020, 65(1/2): 87-95.

[9] 李正明, 孔茗. VIENNA整流器中点电位平衡控制策略研究[J]. 电测与仪表, 2020, 57(6): 120-125.

LI Zhengming, KONG Ming. Research on midpoint potential balance control strategy of VIENNA rectifier[J]. Electrical Measurement & Instrumentation, 2020, 57(6): 120-125.

[10]袁东林, 邵如平, 许文钱, 等. 基于新型自抗扰控制的VIENNA整流器控制策略[J]. 电力电子技术, 2019, 53(12): 102-105.

YUAN Donglin, SHAO Ruping, XU Wenqian, et al. Research on VIENNA rectifier control strategy based on new active disturbance rejection control[J]. Power Electronics, 2019, 53(12): 102-105.

[11] DANG Chaoliang, TONG Xiangqian, SONG Weizhang. Discrete sliding mode control strategy for a three-phase Boost-type VIENNA rectifier with the CB-PWM[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(4): 607-615.

[12] MA Hui, XIE Yunxiang, SHI Zeyu. Improved direct power control for Vienna-type rectifiers based on sliding mode control[J]. IET Power Electronics, 2016, 9(3): 427-434.

[13]黄辉先, 汤湘宁. 基于模糊滑模控制的三相PWM整流器仿真[J]. 电源技术, 2013, 37(5): 836-839.

HUANG Huixian, TANG Xiangning. Simulation of PWM rectifier based on fuzzy reaching law of sliding mode variable structure control[J]. Chinese Journal of Power Sources, 2013, 37(5): 836-839.

[14]杨俊伟, 史旺旺. 交流电流直接控制的单相PWM整流器非线性控制策略[J]. 电力系统保护与控制, 2015, 43(20): 114-118.

YANG Junwei, SHI Wangwang. Nonlinear control strategy for direct AC current control in single-phase PWM rectifier[J]. Power System Protection and Control, 2015, 43(20): 114-118.

[15]王君力, 张安堂, 李彦斌, 等. 三相四线制VIENNA整流器改进单周期控制的仿真研究[J]. 电力系统保护与控制, 2016, 44(18): 88-95.

WANG Junli, ZHANG Antang, LI Yanbin, et al. Simulation study on three-phase four-wire VIENNA rectifier based on advanced one cycle control strategy[J]. Power System Protection and Control, 2016, 44(18): 88-95.

[16]HAN Honggui, WU Xiaolong, ZHANG Lu, et al. Self-organizing RBF neural network using an adaptive gradient multiobjective particle swarm optimization[J]. IEEE Transactions on Cybernetics, 2019, 49(1): 69-82.

[17]乔俊飞, 孙玉庆, 韩红桂. 改进K-means算法优化RBF神经网络的出水氨氮预测[J]. 控制工程, 2018, 25(3): 375-379.

QIAO Junfei, SUN Yuqing, HAN Honggui. Prediction of effluent ammonia nitrogen based on improved K-means algorithm optimizing RBF neural network[J]. Control Engineering, 2018, 25(3): 375-379.

[18]杨道宽, 王久和, 李建国. 不平衡电网下Vienna整流器混合无源控制研究[J]. 燕山大学学报, 2019, 43(5): 408-416.

YANG Daokuan, WANG Jiuhe, LI Jianguo. Research on hybrid passivity based control of Vienna rectifier under unbalanced grids[J]. Journal of Yanshan University, 2019, 43(5): 408-416.

[19]宋卫章, 余丰, 戴智豪, 等. 带负载电流前馈的VIENNA整流器PR控制[J]. 电机与控制学报, 2019, 23(5): 76-83.

SONG Weizhang, YU Feng, DAI Zhihao, et al. Proportional resonant current control strategy with load current feed-forward control for VIENNA rectifier[J]. Electric Machines and Control, 2019, 23(5): 76-83.

[20]郑春菊, 孟鑫, 周群, 等. 三相多驱动系统带移相电流控制的谐波消除方法[J]. 电力系统保护与控制, 2021, 49(12): 114-123.

ZHENG Chunju, MENG Xin, ZHOU Qun, et al. Harmonic elimination method with phase-shifted current control in a three-phase multi-drive system[J]. Power System Protection and Control, 2021, 49(12): 114-123.

[21]袁义生, 陈旭, 毛凯翔. 基于纹波电压前馈的级联H桥整流器输出电压平衡策略[J]. 电力系统保护与控制, 2020, 48(2): 9-17.

YUAN Yisheng, CHEN Xu, MAO Kaixiang. Output voltage balance strategy based on ripple voltage feedforward for cascaded H-bridge rectifier[J]. Power System Protection and Control, 2020, 48(2): 9-17.

[22] XIA Yang, GOU Bin, XU Yan. A new ensemble-based classifier for IGBT open-circuit fault diagnosis in three- phase PWM converter[J]. Protection and Control of Modern Power Systems, 2018, 3(4): 364-372.

[23] REDDY D, RAMASAMY S. Design of RBFN controller based boost type Vienna rectifier for grid-tied wind energy conversion system[J]. IEEE Access, 2018, 6: 3167-3175.

[24]刘喜梅, 王宁, 张硕博. 基于CPS-SPWM的模块化多电平整流器的研究与应用[J]. 电力系统保护与控制, 2020, 48(22): 180-187.

LIU Ximei, WANG Ning, ZHANG Shuobo. Research and application of a modular multilevel rectifier based on CPS-SPWM[J]. Power System Protection and Control, 2020, 48(22): 180-187.

[25]宋平岗, 朱维昌, 戈旺. 基于微分平坦理论的单相PWM整流器直接功率控制[J]. 电力系统保护与控制, 2017, 45(5): 38-44.

SONG Pinggang, ZHU Weichang, GE Wang. Differential flatness based direct power control for single-phase PWM rectifier[J]. Power System Protection and Control, 2017, 45(5): 38-44.

[26]任鹏飞, 耿世勇. 基于H_∞和L_2干扰抑制的PWM整流器双闭环控制[J]. 电力系统保护与控制, 2018, 46(9): 43-48.

REN Pengfei, GENG Shiyong. Double closed-loop control of PWM rectifier based onH_∞ and L_2 disturbance suppression[J]. Power System Protection and Control, 2018, 46(9): 43-48.

[27]马辉. 三相VIENNA整流器调制技术及非线性控制策略研究[D]. 广州: 华南理工大学, 2016.

MA Hui. Research on modulation and nonlinear control strategy for three-phase VIENNA rectifier[D]. Guangzhou: South China University of Technology, 2016.

Vienna rectifier with voltage outer loop sliding mode control based on an RBF neural network

YANG Xuhong1, CHEN Yang1, JIA Wei2, FANG Jianfeng1, LUO Xin1, GAO Zixuan1

(1. School of Automation Engineering, Shanghai Electric Power University, Shanghai 200090, China; 2. Shanghai Solar Energy Engineering Technology Research Center, Shanghai 200241, China)

A Vienna rectifier is used as the research object, and an adaptive voltage outer loop sliding mode control algorithm based on the approximation rate is analyzed for its traditional voltage outer loop sliding mode variable structure control invariance and sensitivity to system parameter perturbation. By effectively combining the RBF neural network with the sliding mode control algorithm, the algorithm also adds the midpoint potential balance control to the design of the RBF neural network adaptive voltage outer-loop sliding mode control algorithm. It uses the RBF neural network for adaptive approximation of the voltage outer-loop nonlinear system. This can effectively reduce the switching gain, weaken the jitter and enhance the anti-interference capability of the system. Lastly, simulation analysis and experimental tests are conducted to verify the effectiveness of the proposed control algorithm. The algorithm is compared with the traditional sliding mode control algorithm and the PI control algorithm, and the results show that the use of this voltage external loop control algorithm can provide fast tracking of the target value of the DC output voltage and balanced midpoint potential. This improves the dynamic and static performance of the system and enhances its anti-interference capability.

Vienna rectifier; voltage outer ring; sliding mode variable structure control; near rate; RBF neural network

10.19783/j.cnki.pspc.211361

2021-10-08；

2021-11-23

杨旭红(1969—)，女，通信作者，博士，教授，研究方向为智能电网控制技术、火电和核电机组的仿真建模及控制技术等。E-mail: yangxuhong.sh@163.com

This work is supported by the National Natural Science Foundation of China (No. 51777120).

国家自然科学基金项目资助(51777120)；上海市2021年度“科技创新行动计划”项目资助(21DZ1207502)

(编辑 魏小丽)