非全相运行对线路零序电流保护的影响分析

郝奕华，陈朝晖，何进锋,3，李银红，石东源

非全相运行对线路零序电流保护的影响分析

郝奕华1，陈朝晖2，何进锋2,3，李银红1，石东源1

(1.强电磁工程与新技术国家重点实验室(华中科技大学)，湖北 武汉 430074；2.中国南方电网电力调度控制中心，广东 广州 510663；3.贵州电网有限责任公司六盘水供电局，贵州 六盘水 553001)

非全相运行是电力系统中一种常见的不对称运行状态，可能会对线路零序电流保护造成影响，使其失去选择性，发生越级动作。为此，研究了线路零序电流保护的整定计算原则，推导了发生短路故障和出现非全相运行状态时零序分支系数的计算公式，对两种情况下的零序分支系数计算公式进行了对比分析，并在此基础上分析了非全相运行状态下零序电流保护越级动作的原因，与短路故障相比，非全相运行时的零序分支系数越大，越容易发生越级动作。结合IEEE39节点系统算例，验证了非全相运行时零序分支系数的增大可能引起线路零序电流保护发生越级动作。最后，针对非全相运行时零序电流保护可能越级动作这一问题，从定值离线校验和在线管理两个方面给出了应对策略。

非全相运行；线路零序电流保护；整定计算；零序分支系数；越级动作

0 引言

零序电流保护由于在改善接地保护灵敏性等方面具有显著的特点，被广泛应用于110 kV及以上电压等级的电网中[1-2]，作为输电线路的后备保护投入使用。为了保证零序电流保护动作的选择性，避免出现越级动作的情况，在零序电流保护整定计算过程中，应保证待整定保护的保护范围不越过相邻设备保护的保护范围。考虑到110 kV及以上电网呈现多电源[3-7]、多环网[8-10]的结构特征，为了实现待整定线路保护和相邻线路保护的保护范围配合，引入了零序分支系数的概念。零序分支系数，即相邻线路保护的保护范围末端发生故障时，流过待整定保护和相邻线路保护零序电流的比值。这里的故障，通常仅考虑了短路故障。

非全相运行状态是电力系统一种常见的不对称运行状态。某一线路单相接地短路后故障相开关跳闸、输电线路一相或两相断线、开关合闸过程中三相触头不同时接通等原因都会导致电力系统处于非全相运行状态[11]。与短路故障相比，非全相运行状态是一种纵向不对称故障，故障端口的构成不同，故障后电气量的分布也不同。考虑到电力系统中的保护定值通常仅按照短路故障进行整定计算，非全相运行状态可能会导致保护的性能受到影响。

文献[12]分析了非全相运行对距离保护的影响，指出两相运行期间方向阻抗继电器的性能将恶化，可能引起保护误动。文献[13]指出非全相运行会对振荡闭锁元件造成影响，从而影响距离保护的动作速度。文献[14]分析了非全相运行对方向高频保护的影响，指出非全相运行情况下会对故障位置造成误判，导致高频零序方向保护误动。文献[15-18]指出发电机机端断路器易发生非全相故障，并提出了新的发电机非全相保护方案。文献[19]分析了非全相运行时的电气特征及导致零序方向保护误动的机理。文献[20-22]指出非全相运行期间产生的零序电流会造成零序电流保护失去选择性，发生越级动作情况，但是没有具体分析零序电流保护越级动作的原因。目前，鲜有文献涉及非全相运行状态下零序分支系数的变化特征以及非全相运行状态下零序电流保护越级动作的原因分析。

为此，本文首先介绍了线路零序电流保护的整定计算原则，然后推导了短路故障和非全相运行状态下零序分支系数的计算公式并对比了其差异，接着分析了非全相运行状态下零序电流保护越级动作的原因，最后结合IEEE39节点系统算例进行了验证。

1 线路零序电流保护的整定计算原则

零序电流保护整定计算的基本目标是保证保护动作的选择性和灵敏性。本节以三相重合闸的四段式线路零序电流保护[23]为例，简要说明线路零序电流保护的整定计算原则。

四段式线路零序电流保护中，零序I段为无延时保护，其电流定值主要考虑保护动作的选择性，按同时躲过本线路区外故障最大零序电流和断路器三相不同步合闸出现的零序电流整定。零序II、III、IV段为带延时保护，其保护范围可能伸出本线路末端。为了保证保护动作的选择性，其电流定值需与相邻线路保护的保护范围进行配合，即不越过相邻线路保护的保护范围末端；其时间定值需与相邻线路保护的动作时间进行配合，即大于相邻线路保护的动作时间一个时延。

以本线路零序IV段和相邻线路零序III段配合为例，其整定计算公式如式(1)、式(2)所示。

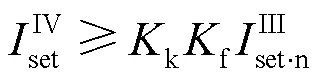
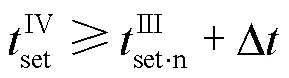
若计算所得的配合定值不满足灵敏度要求，则再与相邻线路保护保护范围较长的段重新进行选择性配合，提升配合定值的灵敏性。仍以零序IV段和相邻线路零序III段配合为例，如果所得定值不满足灵敏度要求，可以与相邻线路零序IV段进行配合，其整定计算公式与式(1)、式(2)类似，将配合定值替换为相邻线路的Ⅳ段定值。

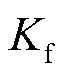
以图1所示系统为例，当计算保护1与保护2的零序分支系数时，通常假设母线k处发生短路故障，然后计算此时流过线路mn的零序电流mn与流过线路nk的零序电流nk的比值。

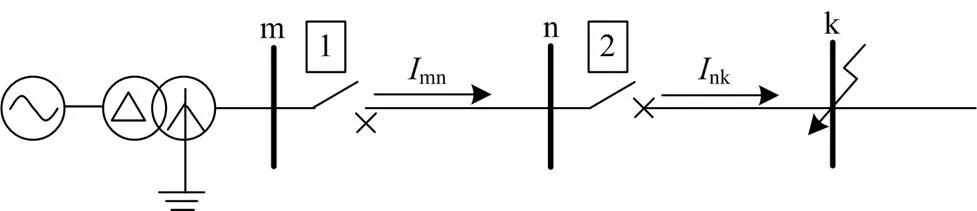
图1 某系统简图

2 零序分支系数计算公式推导及对比分析

在非全相运行状态下，由于故障端口的构成与短路故障不同，零序电流的分布情况也不同。考虑到零序电流保护的选择性主要通过计算故障状态下的零序分支系数来保证，本节将以图2所示系统为例，针对线路kl末端母线l发生短路故障、线路kl发生非全相运行状态两种情况，推导两正常线路保护(即保护1与保护2)之间的零序分支系数、正常线路与故障线路保护(即保护2与保护3)之间的零序分支系数的计算公式，对比分析零序分支系数的差异，为研究非全相状态对零序电流保护的影响奠定基础。

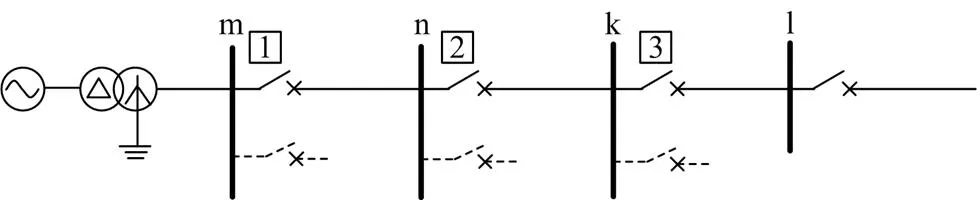
图2 系统结构示意图

2.1 短路故障下的零序分支系数

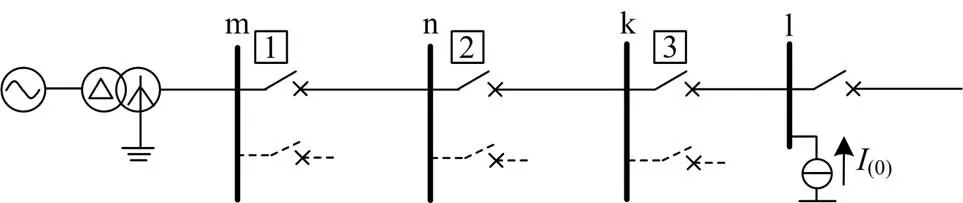
图3 短路故障下零序分支系数计算模型

步骤3：计算流过保护1、保护2和保护3的零序电流，分别如式(3)—式(5)所示。

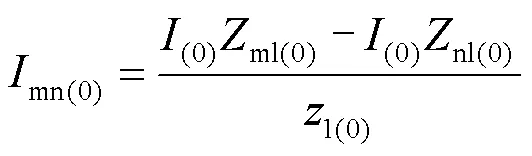
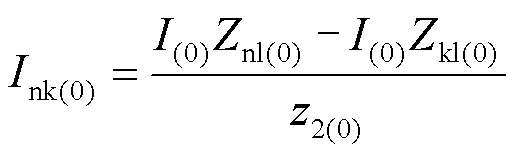
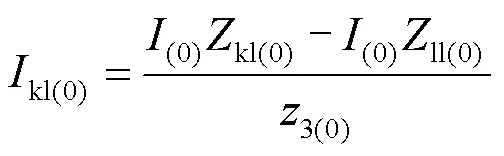
步骤4：计算流过保护1与保护2、保护2与保护3的零序电流的比值，其计算公式如式(6)、式(7)所示。

2.2 非全相运行状态下的零序分支系数

线路kl处于非全相状态时，将保护1与保护2、保护2与保护3的零序分支系数分别记为12、23，其计算具体步骤如下。

图4 非全相运行状态下零序分支系数计算模型

步骤4：分别计算流过保护1、保护2和保护3的零序电流，如式(9)—式(11)所示。

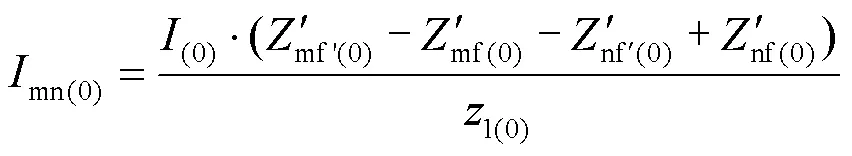
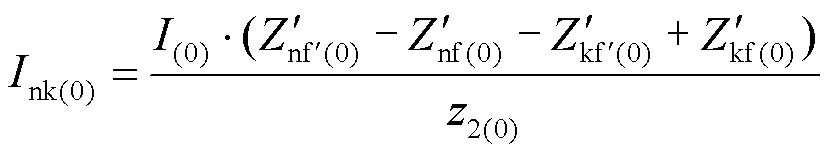
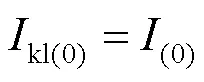
步骤5：计算流过保护1与保护2、保护2与保护3的零序电流的比值，如式(12)、式(13)所示。

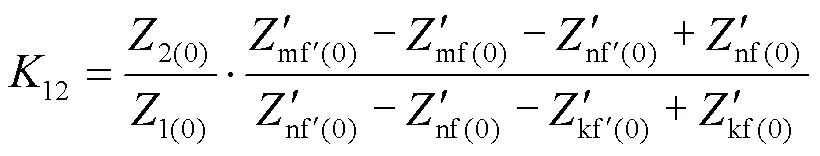
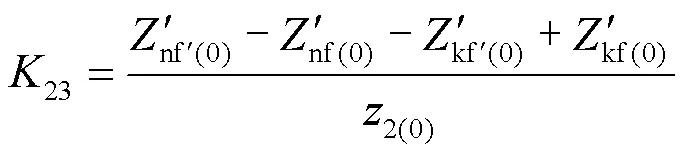
根据零序阻抗矩阵元素关系及式(8)，对式(12)、式(13)进行修改，将表达式中修改后的零序阻抗矩阵元素替换为故障前零序阻抗矩阵的元素，得到式(14)、式(15)。

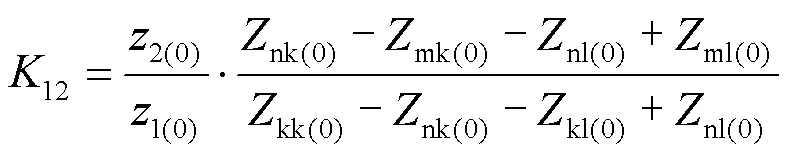
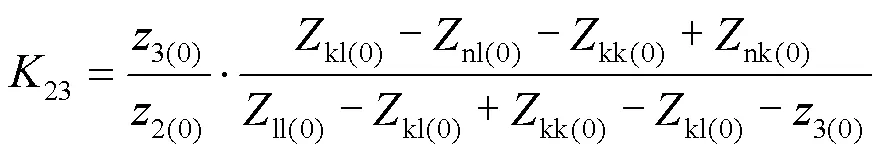
2.3 零序分支系数对比分析

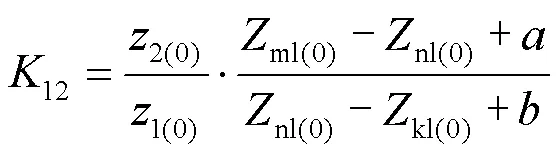
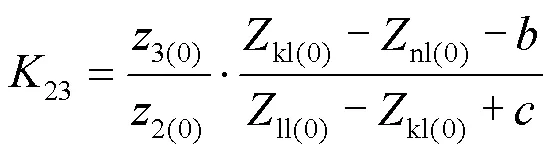
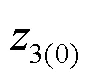
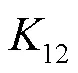
3 非全相运行状态下零序电流保护越级动作原因分析

根据前述分析，在非全相运行状态下，随着常数项大小的不同，零序分支系数与短路故障下相比也不同，可能出现变小、不变或者变大的情况。由于零序电流保护通常仅按照短路故障进行整定计算，因此当系统处于非全相运行状态时，零序电流保护的性能可能会受到影响，失去选择性，发生越级动作的情况。本节以零序电流保护IV段为例，分析零序电流保护越级动作的产生原因。

3.1 基于短路故障的保护定值整定

以图2中保护2的IV 段为例，假设按照短路故障下保护2的IV段与保护3的III段配合进行整定，则保护2的IV段定值满足式(18)所示条件。

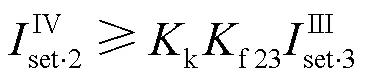
按照上述计算公式，保护2的IV段保护范围不越过保护3的III段保护范围，发生短路故障时，保护2的零序IV段满足选择性要求。如图5所示，在保护3的III段保护范围内发生短路故障时，保护3优先动作。

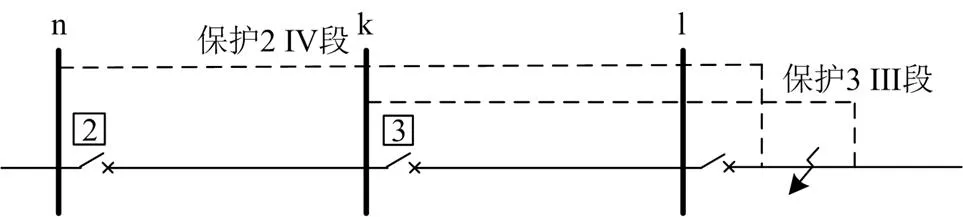
图5 零序电流保护范围

3.2 非全相状态下的保护配合关系分析

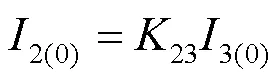
忽略式(18)中的可靠系数，并假定整定值取等号，将式(18)、式(19)两边分别相除，可以得到等式(20)。

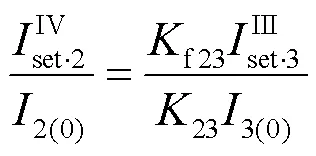
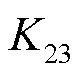
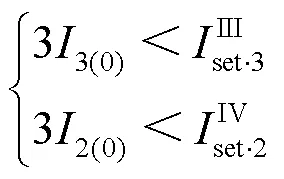
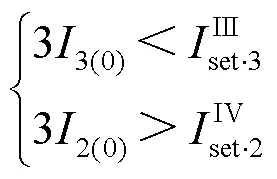
该现象还可以以图6为例进一步说明。

图6 零序电流保护越级动作示意图

综上所述，可得以下结论。

1) 当线路处于非全相运行状态时，由于故障端口的构成不同，零序分支系数与短路故障情况不同，当非全相运行状态下零序分支系数与短路故障下零序分支系数相比变大时，按短路故障进行整定计算得到的零序电流保护定值，在非全相运行状态下可能失去选择性，发生越级动作。

2) 当非全相运行状态下零序分支系数与短路故障下零序分支系数相比增大的值越大时，越容易发生越级动作。

4 算例分析

4.1 算例系统概况

本文算例采用IEEE39节点系统，系统示意图如图7所示。该系统包含10台发电机和46条支路，发电机、节点、支路参数采用IEEE39节点系统标准参数。

图7 IEEE39节点系统示意图

4.2 非全相运行状态与短路故障下零序分支系数对比

取IEEE39母线系统中的节点3、4、5、6分别对应图2中的母线m、n、k、l，分别按式(6)、式(7)、式(14)和式(15)计算母线l发生不对称接地短路故障和线路kl处于非全相运行状态下保护1与保护2、保护2与保护3的零序分支系数。根据IEEE39节点系统参数，得到计算所需的零序阻抗矩阵参数及线路参数，如表1所示。零序分支系数对比如表2所示。

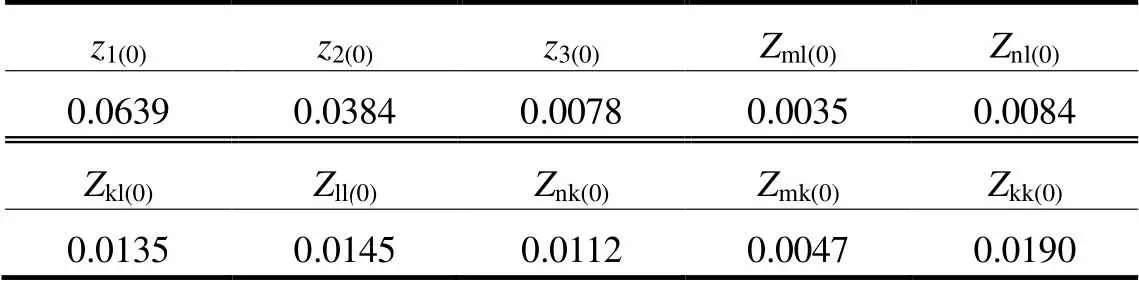
表1 算例1零序阻抗矩阵参数及线路参数

表2 算例1零序分支系数对比

表2结果显示，受非全相运行状态下故障端口变化的影响，在非全相运行状态下零序分支系数12与23均小于短路故障下零序分支系数f12与f23。

取图7中的节点4、3、2、25分别对应图2中的节点m、n、k、l，此时计算所需的零序阻抗矩阵参数及线路参数如表3所示，零序分支系数对比如表4所示。

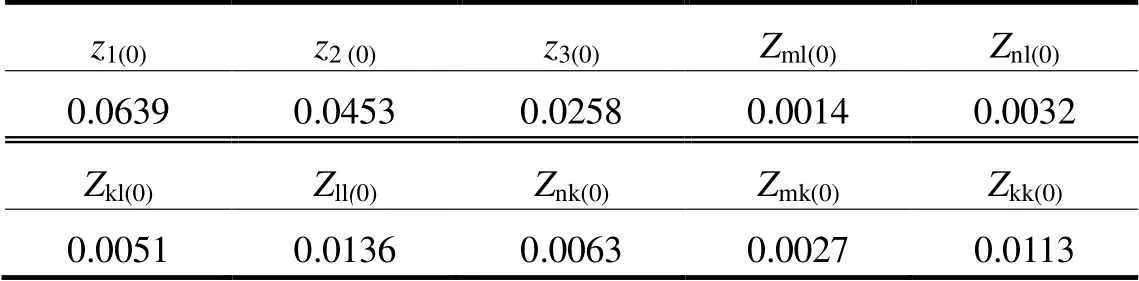
表3 算例2零序阻抗矩阵参数及线路参数

表4 算例2零序分支系数对比

表4结果显示，受非全相运行状态下故障端口变化的影响，在非全相运行状态下零序分支系数12小于短路故障下零序分支系数f12，非全相运行状态下零序分支系数23大于短路故障下零序分支系数f23。

遍历IEEE39节点系统中所有与图2中保护1、保护2和保护3配合关系相符的结构，共166个。统计其零序分支系数情况，结果如表5所示。

表5 IEEE39节点系统零序分支系数情况

根据表5可知，在非全相运行状态下，由于故障端口与短路故障不同，非全相运行状态下零序分支系数与短路故障相比会表现出不同的性质。

4.3 非全相运行状态下零序电流保护越级动作分析

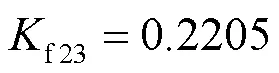
通过算例分析可以发现，由于非全相运行状态下故障端口的位置与短路故障不同，零序分支系数的大小也不同。当非全相运行状态下的零序分支系数大于短路故障下的零序分支系数时，按照短路故障进行整定计算得到的定值很可能不适用于非全相运行的情况，从而导致在非全相运行状态下零序电流保护发生越级动作。

5 应对策略

根据前述分析，非全相运行可能导致零序电流保护失去选择性，发生越级动作。因此，本节从定值离线校验和在线管理两方面给出了应对策略。

5.1 定值离线校验

定值离线校验即在通过整定计算得到一组零序电流保护的定值后，校验在非全相运行情况下定值是否能满足选择性要求，不发生越级动作。定值离线校验的流程如下。

1) 确定可能发生非全相运行的线路，计算所有运行条件下线路非全相运行时的零序电流。

2) 当流过非全相运行的线路的零序电流较小时，只需校验非全相运行线路及相邻线路定值能否满足选择性要求。如果不满足，则调整对应保护的定值。

3) 当流过非全相运行的线路的零序电流较大时，需校验非全相运行线路及相邻多级线路的定值能否满足选择性要求。如果不满足，则调整对应保护的定值。

5.2 定值在线管理

继电保护故障信息系统能够实时采集保护设备的信息，支持对保护设备的整定值进行远程修改，为定值的在线管理提供了有利条件[24]。通过定值在线管理的方式可以实时采集电网运行方式变化信息、计算新定值并快速下发定值，更有利于实现保护定值之间的配合，缩短保护动作时间，优化保护性能。可以考虑采用定值在线管理的方式应对非全相运行对零序电流保护的影响。定值在线管理的流程如下。

1) 实时采集电网运行方式变化信息，上传至调度端。

2) 由调度端的在线整定服务器进行在线整定，得到在非全相运行情况下满足选择性的定值。

3) 调度端向保护装置下发新的定值，在线调整定值。

6 结论

由于非全相运行状态下故障端口位置与短路故障不同，零序分支系数的大小也不同，所以可能导致按短路故障进行整定计算得到的定值在非全相运行状态下失去选择性，从而出现发生越级动作的情况。本文首先给出了线路零序电流保护的整定计算原则，然后推导了短路故障和非全相运行状态下零序分支系数的计算公式并对比了其差异，非全相运行状态下零序分支系数与短路故障下零序分支系数计算公式形式类似，但是在非全相运行状态下零序分支系数的计算公式中分子分母分别添加了一个常数项，常数项会影响零序分支系数的大小，使非全相运行状态下零序分支系数与短路故障下零序分支系数相比表现出大于、等于或小于的不同性质。接着分析了非全相运行状态下零序电流保护越级动作的原因，当非全相运行状态下零序分支系数与短路故障下零序分支系数相比变大时，容易发生越级动作情况。之后结合IEEE39节点系统进行了算例分析。算例分析结果验证了非全相运行对零序电流分布的影响，表明非全相运行状态可能使零序电流保护失去选择性，发生越级动作情况。从定值离线校验和在线管理两方面出发，给出了非全相运行状态下零序电流保护越级动作问题的应对策略。

[1] 张保会, 尹项根. 电力系统继电保护[M]. 北京: 中国电力出版社, 2010.

[2] 张培夫, 金能, 章建玲, 等. 一种面向线路零序过流保护的防励磁涌流所致误动闭锁策略[J]. 中国电机工程学报, 2020, 40(23): 7609-7622.

ZHANG Peifu, JIN Neng, ZHANG Jianling, et al. A line zero-sequence over current protection blocking strategy against maloperation caused by inrush[J]. Proceedings of the CSEE, 2020, 40(23): 7609-7622.

[3] 王艺, 王宾, 刘阳, 等. 计及分布式电源动态行为的配电网重构优化策略[J]. 电力系统保护与控制, 2020, 48(24): 164-172.

WANG Yi, WANG Bin, LIU Yang, et al. Optimization strategy for distribution network reconfiguration considering the dynamic behavior of DGs[J]. Power System Protection and Control, 2020, 48(24): 164-172.

[4] DAS T, ROY R, MANDAL K K. Impact of the penetration of distributed generation on optimal reactive power dispatch[J]. Protection and Control of Modern Power Systems, 2020, 5(4): 332-357.

[5] 王秀强. 新型电力系统构建“源网荷储”新生态[J]. 能源, 2021(7): 28-30.

WANG Xiuqiang. New power system to build a new ecology of “source network load storage”[J]. Energy, 2021(7): 28-30.

[6] 李翠萍, 东哲民, 李军徽, 等. 配电网分布式储能集群调压控制策略[J]. 电力系统自动化, 2021, 45(4): 133-141.

LI Cuiping, DONG Zhemin, LI Junhui, et al. Control strategy of voltage regulation for distributed energy storage cluster in distribution network[J]. Automation of Electric Power Systems, 2021,45(4): 133-141.

[7] 潘本仁, 王和春, 张妍, 等. 含分布式电源的主动配电网重构策略研究[J]. 电力系统保护与控制, 2020, 48(15): 102-107.

PAN Benren, WANG Hechun, ZHANG Yan, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107.

[8] 徐泽, 杨伟, 张文强, 等. 基于连锁环网与改进离散粒子群算法的多目标配电网重构[J]. 电力系统保护与控制, 2021, 49(6): 114-123.

XU Ze, YANG Wei, ZHANG Wenqiang, et al. Multi- objective distribution network reconfiguration based on chain loops and improved binary particle swarm optimization[J].Power System Protection and Control, 2021, 49(6): 114-123.

[9] 贾晓峰, 颜伟, 周家启, 等. 复杂电网的分层解耦潮流算法[J]. 中国电机工程学报, 2010, 30(7): 56-61.

JIA Xiaofeng, YAN Wei, ZHOU Jiaqi, et al. Layer- decoupled power flow algorithm for complex networks[J]. Proceedings of the CSEE, 2010, 30(7): 56-61.

[10] 翁蓝天, 王禹民, 刘开培, 等. 链表拓扑环境下基于配网结构特点的多源有环短路计算[J]. 电工技术学报, 2010, 25(10): 150-157.

WENG Lantian, WANG Yumin, LIU Kaipei, et al. Multi-power short circuit calculation on middle and lower voltage distribution grid’s structure characteristics[J].Transactions of China Electrotechnical Society, 2010, 25(10): 150-157.

[11] 何仰赞, 温增银. 电力系统分析[M]. 武汉: 华中科技大学出版社, 2016.

[12] 邹力, 苗世洪, 刘沛. 高压线路非全相运行对距离保护的影响[J]. 继电器, 2003, 31(5): 1-4.

ZOU Li, MIAO Shihong, LIU Pei. Influence of 2-phase work condition of high voltage transmission line on distance protection relay[J]. Relay, 2003, 31(5): 1-4.

[13] 魏曜, 薛明军. 一种适用于高压线路非全相运行时的距离保护振荡闭锁的开放方案[J]. 电力系统保护与控制, 2016, 44(19): 70-75.

WEI Yao, XUE Mingjun. A new method for opening distance protection when the high voltage transmission lines is non-full-phases operation[J]. Power System Protection and Control, 2016, 44(19): 70-75.

[14] 林峻嵩. 非全相运行对方向高频保护的影响[J]. 广东电力, 2001, 14(4): 16-18.

LIN Junsong. Influence of open-phase running on directional comparison pilot protection[J]. Guangdong Electric Power, 2001, 14(4): 16-18.

[15] 朱子娇, 杨涛, 王慧芳, 等. 发电厂非全相运行电气量计算方法及保护方案[J]. 电力系统及其自动化学报, 2018, 30(10): 97-103.

ZHU Zijiao, YANG Tao, WANG Huifang, et al. Calculation method and protection Scheme of power plant in open-phase operation[J]. Proceedings of the CSU-EPSA, 2018, 30(10): 97-103.

[16] 贺儒飞, 李荷婷. 发电机机端断路器非全相保护新型判据的研究[J]. 电力系统保护与控制, 2018, 46(17): 165-170.

HE Rufei, LI Heting. Research on the new open-phase protection criterions of the generator circuit breaker[J]. Power System Protection and Control, 2018, 46(17): 165-170.

[17] 陈俊, 李华忠, 徐青山, 等. 基于断口两侧电压相量差的发电机机端断路器非全相保护[J]. 电力系统自动化, 2018, 42(21): 125-130.

CHEN Jun, LI Huazhong, XU Qingshan, et al. Open- phase protection of generator circuit breaker based on voltage phasor differences between two sides of breaking point[J]. Automation of Electric Power Systems, 2018, 42(21): 125-130.

[18] 李荷婷, 桂林, 贺儒飞, 等. 基于电压型故障特征量的发电机机端断路器非全相保护[J]. 电力系统自动化, 2017, 41(1): 140-144.

LI Heting, GUI Lin, HE Rufei, et al. Voltage features based open-phase protection of generator circuit breaker[J]. Automation of Electric Power Systems, 2017, 41(1): 140-144.

[19] 戴飞扬, 王兴国, 杨国生, 等. 基于站域信息的同塔多回线零序方向保护防误动方法[J]. 电力系统自动化, 2019, 43(13): 131-138.

DAI Feiyang, WANG Xingguo, YANG Guosheng, et al. Substation information based method for preventing mal-operation of zero-sequence directional protection on multi-circuit transmission lines on the same tower[J]. Automation of Electric Power Systems, 2019, 43(13): 131-138.

[20] 卫琳, 张健康, 粟小华, 等. 大型发电机组非全相保护存在问题及对策[J]. 电网技术, 2020, 44(6): 2336-2342.

WEI Lin, ZHANG Jiankang, SU Xiaohua, et al. Problems and solutions of open-phase protection for large generator-transformer unit[J]. Power System Technology, 2020, 44(6): 2336-2342.

[21] 袁浩, 王琰, 倪益民, 等. 高压线路保护非全相运行状态下的考虑[J]. 电力系统自动化, 2010, 34(20): 103-107.

YUAN Hao, WANG Yan, NI Yimin, et al. Considerations for high voltage line protection under open-pole operation[J].Automation of Electric Power Systems, 2010, 34(20): 103-107.

[22] 刘亚东, 孙集伟, 杨国生, 等. 断线故障对零序过流保护的影响及保护新方法[J]. 电力自动化设备, 2017, 37(7): 130-134, 141.

LIU Yadong, SUN Jiwei, YANG Guosheng, et al. Impact of open-circuit fault on zero-sequence over-current protection and improved protection scheme[J]. Electric Power Automation Equipment, 2017, 37(7): 130-134, 141.

[23] 220 kV-750 kV电网继电保护装置运行规程: DL/T 559—2007[S]. 北京: 中华人民共和国国家发展和改革委员会, 2007.

Setting regulations for relay protection operation of 220 kV-750 kV power networks: DL/T 559—2007[S]. Beijing: National Development and Reform Commission of China, 2007.

[24] 段惠明, 何飞跃, 李志宏, 等. 基于EMS和故障信息系统的在线定值管理系统构想[J]. 电力系统自动化, 2006, 30(10): 97-99, 104.

DUAN Huiming, HE Feiyue, LI Zhihong, et al. Online setting management system based on EMS and fault information system[J]. Automation of Electric Power Systems, 2006, 30(10): 97-99, 104.

Analysis of the influence of non-full-phase operation on line zero-sequence current protection

HAO Yihua1, CHEN Zhaohui2, HE Jinfeng2, 3, LI Yinhong1, SHI Dongyuan1

(1. State Key Laboratory of Advanced Electromagnetic Engineering and Technology (Huazhong University of Science and Technology), Wuhan 430074, China; 2. China Southern Power Grid Power Dispatching and Control Center, Guangzhou 510663, China; 3. Liupanshui Power Supply Bureau, Guizhou Power Grid Co., Ltd., Liupanshui 553001, China)

Non-full-phase operation is a common asymmetric operational state in a power system. It will affect line zero-sequence current protection, causing it to lose selectivity and override. Therefore, the setting calculation principle of line zero-sequence current protection is studied. Then the calculation formulas of the zero-sequence branch coefficient under short-circuit fault and non-full-phase operation are deduced. By comparing the calculation formula of zero-sequence branch coefficient in two cases, the reason for the override of zero-sequence current protection under non-full-phase operation is analyzed. Compared with the zero-sequence branch coefficient of a short-circuit fault, the greater the zero-sequence branch coefficient of non-full-phase operation is, the easier the occurrence of override. Combined with the example of the IEEE39 bus system, it is verified that the increase of zero-sequence branch coefficient may cause the line zero-sequence current protection to override in the condition of non-full-phase operation. Finally, given the problem that zero-sequence current protection may override during non-full-phase operation, coping strategies are given from the two aspects of settings off-line verification and on-line management.

non-full-phase operation; line zero-sequence current protection;setting calculation; zero-sequence branch coefficient; override

10.19783/j.cnki.pspc.211662

2021-12-07；

2022-01-21

郝奕华(1998—)，男，硕士研究生，主要研究方向为电力系统继电保护分析及整定计算。E-mail: haoyihua@ hust.edu.cn

This work is supported by the National Key Research and Development Program of China (No. 2016YFB0900100).

国家重点研发计划项目资助(2016YFB0900100)；国家自然科学基金项目资助(51777081)

(编辑 许 威)