库仑势约束下薛定谔方程的势代数及超对称自发破缺

王海楠，文 莉，程建兰，熊露霖，罗 光

(重庆师范大学物 理与电子工程学院，重庆 401331)

超对称量子力学于1981年由Witten一经提出[1]，就受到人们的广泛关注，并且超对称思想很快就被应用到诸如场论等其他领域[2-4]. 超对称量子力学及其势代数形式在讨论薛定谔方程的求解时也有重要应用，是实现精确求解的一种非常重要的方法[4，5]. 目前，各种势约束下的薛定谔方程的精确求解或者准精确求解问题一直以来都是量子力学中特别关注的问题[6-11]，而基于超对称量子力学，能够求解的势约束下的薛定谔方程多达十几种[3，10，12]. 这些势主要有谐振子势、库仑势、Morse势、Rosen-Morse势、Scarf势、Eckart势、Pösch-Teller 势等[3，8].

库仑势作用下的薛定谔方程的求解也是量子力学中的经典问题[13，14]，不过处理过程相对繁琐.基于超对称量子力学处理库仑势问题，过程和结果相当简洁明了[15，16].虽然如此，库仑势作用下的薛定谔方程的讨论依然还有一些有待处理的问题，比如由于在r→0时，库仑势是发散的，一般是考虑采取截断处理[17]；以及针对零能基态波函数中的轨道角动量量子数l的取值，即l<-1时，波函数不满足归一化从而出现超对称自发破缺.

本文基于超对称量子力学方法，对库仑势作用下的薛定谔方程的求解做了进一步讨论.首先，针对给出了径向方程和角向方程的形状不变性关系和势代数理论，导出了势代数形式的形状不变关系，满足SO(2，1)群对称性；然后讨论了径向波函数和角向波函数的敛散性，讨论了系统出现的超对称破缺，并且采用超对称破缺系统的两步形状不变性，通过调整参数取值，重新获得了伴随势遵循的形状不变性.

1 超对称量子力学简介

为简便计算，设ћ=2m=1，定态薛定谔方程的哈密顿量为

(1)

根据有关文献[2-7]引入超势W(x，a)，定义升降算符A+与A-：

(2)

体系的势转化为两个伴随势V±(x，a)来描述：

(3)

且伴随势V±(x，a)之间满足：

V+(x，a0)=V-(x，a1)+R(a0)

(4)

其中R(a0)是一个相加性常数，且a1=f(a0).形状不变性也可以用升降算符A±(x，a)来表示：

A+(x，a0)A-(x，a0)-A-(x，a1)A+(x，a1)=R(a0)

(5)

相应的伴随哈密顿量为

(6)

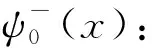
(7)

以及相应的能量本征值谱.

2 超对称量子力学处理具有库仑势的薛定谔方程

库仑势作用下球坐标定态薛定谔方程为[13，15]

(8)

设ψ=R(r)Y(θ，φ)分离变数后，得

(9)

(10)

进一步分离Y(θ，φ)满足的方程，令Y(θ，φ)=Θ(θ)Φ(φ)，得

(11)

[l(l+1)sin2θ-m2]Θ(θ)=0

(12)

令u(r)≡rR(r)，代入式(9)可得

(13)

再令sinθ=shz，代入式(12)，得

(l2-m2)Θ(z)

(14)

式(11)、(13)、(14)都可以用超对称量子力学思想处理[3，6]，它们的超势分别为:

W1(φ，m)=m，

W3(z，l)=lthz

(15)

满足式(4)的形状不变关系分别为:

(16)

(17)

(18)

根据式(7)，可得出式(11)、(13)和(14)对应的零能基态波函数：

(19)

(20)

(21)

其中，N1、N2和N3为归一化系数.可以依据式(2)的升降算符作用到上述基态波函数上，可得出对称形式的伴随哈密顿量的本征波函数.

3 形状不变性的势代数形式

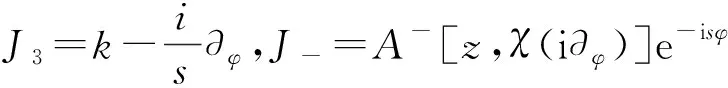
[J3，J+]=J+和[J3，J-]=-J-

(22)

这样的性质.另外算符J+、J-和J3还有以下的性质：

(23)

而且J±也满足对易关系：

[J+，J-]=f(J3)

(24)

式(24)即为势代数情形下的形状不变性关系.根据f(J3)，可以确定系统具有的对称性[11].

3.1 径向方程代数形式的形状不变性关系

(25)

可以计算出

(26)

选择k=-1，形状不变性的势代数形式最简单

(27)

即为径向方程式(13)对应的形状不变关系.

3.2 Θ(z)满足的方程的代数形式的形状不变性关系

Θ(z)满足的方程为式(14)，其超势为W3(z，l)=lthz，再据a0=-l，a1=-l+1可确定s=1，用k-J3替换-l，对应的J+与J-分别为

(28)

可以计算出

[J+，J-]=2(k-J3)+1

(29)

选择k=-1，形状不变性的势代数形式最简单：

[J+，J-]=-2J3

(30)

即为式(14)势代数描述下的形状不变关系，且满足SO(2，1)群对称性.

3.3 Φ(φ)满足的方程的代数形式的形状不变性关系

Φ(φ)满足的方程为式(11)，其超势为W3(φ，m)=m，再根据a0=m，a1=m+1可确定s=1，用k-J3替换m，对应的J+与J-分别为

(31)

可得出J+与J-的对易关系为

[J+，J-]=2(k-J3)+1

(32)

[J+，J-]=-2J3

(33)

即为常微分方程式(11)势代数描述下的形状不变关系，且系统满足SO(2，1)群对称性.

4 库仑势的超对称自发破缺讨论

4.1 径向方程波函数的超对称自发破缺

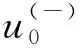
(34)

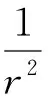
(l+1)(l+2)=a1(a1+1)

(35)

可解得a1=l+1，式(17)的形状不变性就是选择的这个取值.式(35)还有另一个解a1=-l-2，如果针对l<-1的情形，我们发现-l-2≥0，代入式(34)，此时波函数恰好又是收敛了，自发破缺问题解决了.因此，选择a1=-l-2，依然有

(36)

只不过这是调整参数后的形状不变形式.根据超对称量子力学，易算得

(37)

利用迭代思想，可计算出整个能谱和本征波函数.

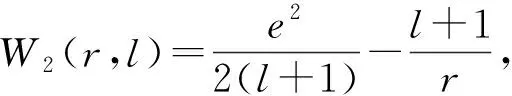
(38)

可以计算出

(39)

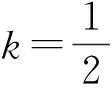
(40)

即为径向方程(9)出现超对称自发破缺后，采用两步法调整参数后转变为满足超对称关系的对应的形状不变关系的势代数形式.

4.2 Θ(z)满足的方程波函数的超对称自发破缺

根据式(7)，把W3(z，l)=lthz代入，可得零能基态波函数为

(41)

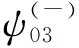
l(l-1)=a1(a1+1)

(42)

可解得a1=l+1，式(18)的形状不变性就是选择的这个取值.式(41)还有另一个解a1=-l，如果针对l<-1的情形，我们发现-l>0，代入式(41)，此时虽然波函数恰好又是收敛了，似乎自发破缺问题解决了，但是由于a1=-l与a0=l之间并未表现出加性特征，所以不满足形状不变性.因此利用形状不变性和势代数法无法处理这种同谱势问题.

5 总结

基于超对称量子力学研究了库仑势约束下的薛定谔方程经分离变数后的径向以及角向方程的势代数法求解.首先，对超对称量子力学做了简介，然后，依据库仑势的超势得出伴随势的形状不变性，进而得到零能量本征值和本征波函数；第三，基于势代数法讨论了库仑势约束下的径向以及角向方程势代数形式的形状不变关系；最后，针对波函数中l的取值情况，讨论了径向波函数出现超对称自发破缺以后，通过参数调整的两步法进而解决了超对称破缺的问题.