考虑光伏不确定性因素的电力系统概率潮流三点估计法

高明，陈家豪，王丽晓，唐武琛，王智东，张紫凡，马海霞，冯瑞珏，周长鹏

（1.广州城市理工学院电气工程学院，广州 510800；2.宜通世纪物联网研究院（广州）有限公司，广州 510665；3.华南理工大学电力学院智慧能源工程技术研究中心，广州 510640）

0 引言

随着中国能源战略的改变，可再生能源发电成为研究热点，经过近10 年的快速发展，间歇性可再生能源已成为我国重要的能源供应形式之一［1］。

光伏作为可再生能源的重要组成部分，装机容量逐年提升，截至2020 年年末，我国光伏发电累计装机已经达到253.43 GW［2］。而光伏发电具有随机性和波动性，其在电网发电的比例越高，给电力系统运行状态带来的影响越不容忽略［3］。

但传统的确定性潮流无法准确反映系统真实运行状况，故提出概率潮流算法理论，这一概念最早是在1974 年由Brokowska 提出并应用于电力系统潮流计算中［4］。

根据现有概率潮流计算方法的工作原理，可将其大致分成以下3 类：蒙特卡洛仿真法（Monte Carlo Simulation，MCS）、解析法、近似法［5-6］。

MCS 是一种以概率论和数理统计为基础的试验统计方法，它的收敛性几乎不受系统规模和复杂程度的影响，且在采样规模足够大时具有很高的计算精度，但计算时间难以承受［7］，该方法通常是其他概率潮流算法计算准确度的评估基准。

为了提高MCS 的计算速度，减少采样数量，文献［8］采用基于Sobol序列的拟蒙特卡罗法获得具有随机性的可再生能源出力和负荷的样本，规避了MCS 中的随机抽样。同样，拉丁超立方采样法也可以避免随机大规模采样，文献［9］将Cholesky分解与之相结合。文献［10］将自适应重要抽样与之相结合，都提高了抽样效率。文献［11］对拉丁超立方采样法的采样排序进行改进，提出一种将随机行走原理和拉丁超立方采样相结合的方法，提高了计算精度，更为精确地反映随机变量的数字特征。文献［12］利用概率潮流中的拉丁超立方采样法和Cholesky 分解进行相关性样本的采集，将生成的秩相关系数矩阵加入概率潮流计算中。文献［13］建立了包括储能系统的成本、支路潮流的越限概率和电网的网络损耗在内的多目标优化模型，并用遗传算法求取目标函数的最优解。解析法中主要包括卷积法和半不变量法，可以根据输出随机变量与输入随机变量之间的线性函数关系得到输出随机变量的概率统计特性。为了提高半不变量法的求解精度，文献［14］采用分段线性化的手段来减小潮流方程线性化误差。文献［15］根据光伏出力的概率分布特性，分别采用离散数据法和样条插值法对超拉丁立方抽样法进行改进，并与半不变量法结合，从而也有效提高了概率潮流的计算准确性。在半不变量法输出结果的处理上，文献［16］利用Gram-Charlier级数展开理论，保证结果高度准确的同时提高了计算效率，可以用于处理大型的实际系统。文献［17］比较了基于半不变量法的3 种展开式：Gram-Charlier，Edgeworth，Cornish-Fisher，结果表明这3种方法都能在随机变量近似服从正态分布时得到准确结果。

对于变量的相关性处理，文献［18］提出了一种基于Cholesky 分解的半不变量法，使半不变量法能够应用于输入随机变量具有相关性的场合，同时提出了基于MCS 的方法来解决某些输入变量的半不变量不能被常规数值方法求解的问题。

近似法根据输入随机变量的概率统计特性近似描述输出随机变量的概率统计特性，典型方法为点估计法（Point Estimate Method，PEM），具有计算效率高的优点。

文献［19］比较了4种不同的PEM策略：2m，2m+1，3m，4m，结果表明2m+1 策略在系统拥有大量输入随机变量的情况下，无论处理离散还是连续变量，都具有最佳性能，故本文也采用此策略。一般假设输入随机变量相互独立，而文献［20］结合Nataf变换使PEM 能够处理输入随机变量具有相关性的问题。文献［21-25］均采用了2m+1 策略的三点估计法（Three-Point Estimate Method，3PEM）和Nataf逆变换，而且前者与直流潮流模型相结合提高了计算速度，适用于直流系统，而后者通过增加一组正态分布尾部点的组合克服了3PEM 尾部准确度不足的问题。文献［25］提出一种基于贝叶斯理论的最大期望算法及Rosenblatt 变换的3PEM，能够很好捕捉风电场之间的非线性相关性。文献［26］考虑输入随机变量相关系数矩阵非正定的情形，提出一种主元分析结合Cornish-Fisher级数展开的PEM，能适应新能源发电高渗透率电力系统的快速概率潮流计算。

综上所述，MCS 原理简单而且求解精度高，但往往伴随着计算量大、耗时长的问题，故一般作为其他概率潮流计算方法准确度的参照。

同时，为了避免大规模的采样，本文选择基于超拉丁立法的MCS 来减少运行时间。对于解析法中的半不变量法，其在原理上需要对系统进行线性化处理得到解析式，因而在对潮流方程进行近似化处理的过程中，误差不可避免，故本文决定采用3PEM来计算概率潮流。

对于潮流结果的处理上，文献［27］指出，Cornish-Fisher级数与Gram-Charlier级数相比，在计算非正态分布的概率分布时，具有更高的精度。考虑到本文光伏发电的概率模型属于非正态分布，故本文将采用Cornish-Fisher 级数展开来获得输出随机变量的概率分布。

本文第1 节介绍了光伏发电和负荷的概率模型；第2节介绍了基于3PEM的概率潮流求解的过程与相关理论基础，包括半不变量的定义、3PEM 的原理，以及Cornish-Fisher 级数展开理论；第3 节介绍了算法的完整流程，并在改进的IEEE 33 节点系统进行算例分析，验证了3PEM 的有效性，且分析了光伏接入对电力系统的影响；第4节为本文的结论。

1 概率模型

1.1 光伏出力的概率模型

光照强度是一种不确定的随机变量，本文采用Beta 分布来模拟光照强度的概率分布［21］，其概率密度函数表示为

1.2 负荷的概率模型

负荷功率往往伴随着时间的改变而上下浮动，普通意义上的负荷值表示的是其平均值［28］。

目前较为接受的观点是认为负荷随机变化服从正态分布，因此本文分别用σP和μP为有功功率的方差和期望值，用σQ和μQ为无功功率的方差和期望，则二者的概率密度函数为

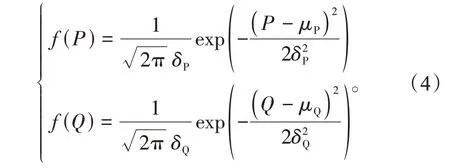
故在已知负荷有功功率和无功功率的期望和方差的前提下，可以通过式（4）求得一组服从正态分布的P，Q值。于是，在极坐标下根据节点功率方程，可以写出负荷节点的节点功率不平衡量方程为

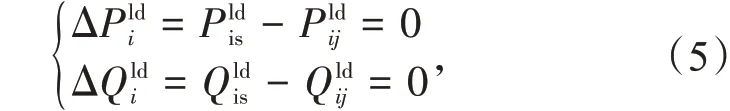
2 基于3PEM的概率潮流求解

2.1 半不变量

半不变量，又称累积量，也是随机变量的一种数字特征［29］。半不变量具有2个重要的性质。

（2）齐次性：相互独立随机变量Ω倍的k阶半不变量等于该随机变量k阶半不变量的Ωk倍。

假设F（x）是随机变量X的一元累积分布函数，令t为任意实数，则在（-∞，+∞）上关于F（x）的积分函数g（x）=ejtx=cos（tx）+jsin（tx）称为F（x）的特征函数，该特征函数具体可表示为

2.2 PEM

在电力系统中，若已知各节点输入随机变量（x1，x2，…，xm）的概率分布，则理论上可通过3PEM利用输入输出的函数关系Z=f（x1，x2，…，xm），求取系统各节点电压与支路潮流的有限阶原点矩［30］。其中，函数关系f为如下交流潮流方程

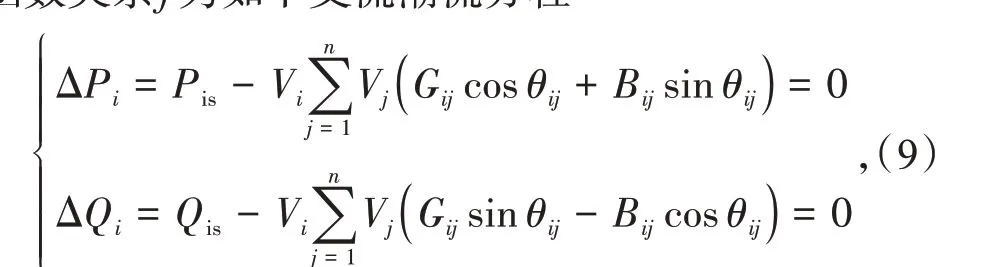
式中：Pis，Qis分别为给定的有功、无功功率。写成矩阵形式为

式中：ΔF=［ΔP；ΔQ］；ΔX=［V；θ］；J为雅可比矩阵。于是，便可以用牛顿-拉夫逊潮流计算方法求得输出变量。

为了便于分析，假设各输入随机变量之间相互独立。根据1.1 和1.2 节建立光伏出力和负荷的概率模型后，求出每一个输入随机变量xk的均值和标准差，记为μk和δk，再用式（11）计算其3 个估计点，记为xk，1，xk，2，xk，3。

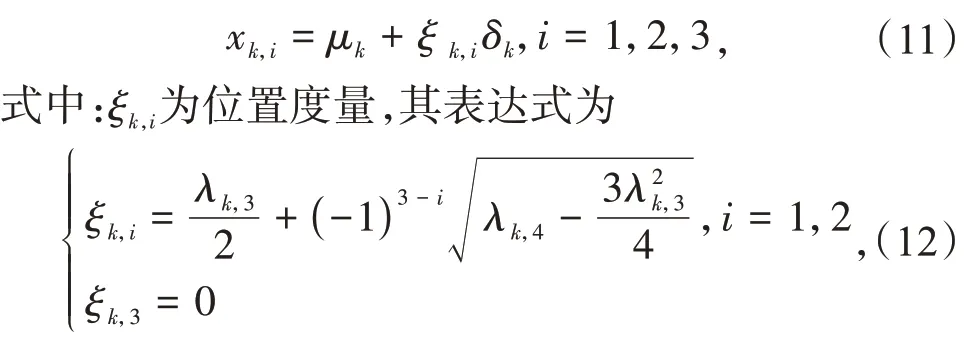
式中：λk，3为随机变量xk的3 阶中心距，称为偏度系数，表示xk的分布偏离标准正态分布的程度；λk，4为随机变量xk的4 阶中心矩，称为峰度系数：若λk，4很小，说明xk的取值集中在期望附近；若为0，说明随机变量xk的分布和正态分布的陡峭度一致。二者的表达式为

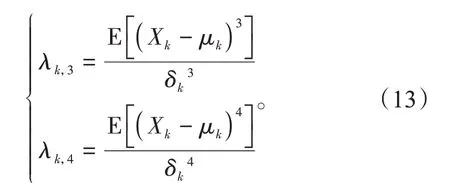
构造出随机变量Xk的3 个估计点后，就可以通过牛顿-拉夫逊潮流计算方法求得输出随机变量的相应估计点。理论上，拥有m个随机输入变量的系统可以获得3m个估计点，从而需要求解3m次潮流方程，但由于ξk，3=0，此位置上所有输入随机变量为各自的均值，即有m个点是相同的，故只需要求解2m+1次潮流方程，减少了计算量。

利用2m+1 次潮流计算得到的节点电压和支路潮流结果，分别计算它们的各阶原点矩为

2.3 Cornish-Fisher展开级数

利用上述PEM 求得的节点电压和支路潮流的期望、方差等原点矩和半不变量后，结合Cornish-Fisher 展开级数［31］可以求出这些输出随机变量的概率密度函数（Probabilistic Density Function，PDF）和累积量分布函数（Cumulant Distribution Function，CDF）。

设输出随机变量Z的概率分布函数为F（z），其分位数为τ，有z（τ）=F-1（τ），则根据Cornish-Fisher级数理论［32］，z（τ）可近似表示为

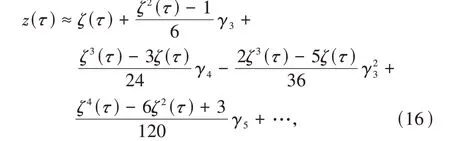
式中：ζ（τ）=Ф-1（τ）；Φ（x）为标准正态分布的CDF；γi为随机变量z的i阶规格化半不变量。

3 算法流程与算例分析

3.1 基于3PEM的概率潮流算法流程

本文算例以MATLAB 为平台，验证模型与算法的准确性与适用性。具体步骤如下。

（1）输入数据。

（2）建立输入随机变量模型。

（3）确定各输入随机变量的3个估计点。

（4）进行确定性潮流计算：取某个随机输入变量的估计点，其余变量保持均值，即在（μ1，μ2，…，xk，i，…，μm）处进行确定性潮流计算，得到输出随机变量的估计值f（μ1，μ2，…，xk，i，…，μm），其中m为输入随机变量个数。

（5）重复步骤（4），直到2m+1次计算结束。

（6）计算输出随机变量的各阶原点矩E（Zj）。

（7）用Cornish-Fisher展开级数求得各输出随机变量的PDF和CDF，并绘制图形。

基于上述步骤，系统的概率潮流计算流程如图1所示。

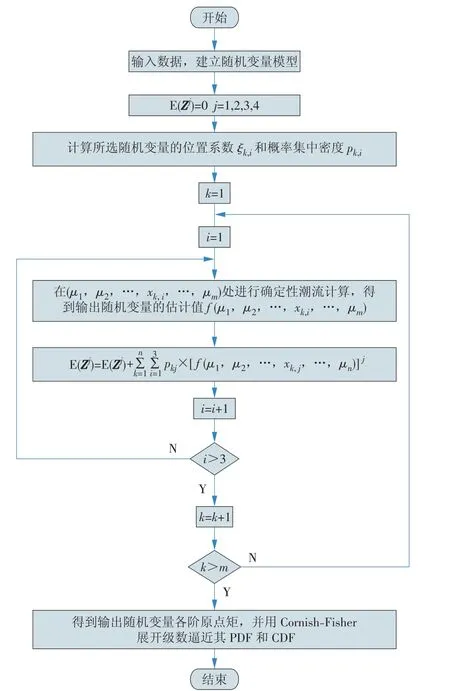
图1 基于3PEM的概率潮流计算流程Fig.1 Probabilistic load flow calculation based on 3PEM

3.2 算例分析

3.2.1 基于3PEM的概率潮流计算有效性验证

本文以IEEE 33 节点系统 为例［33］，为了验证3PEM 的概率潮流计算的准确性，用MCS 得到的结果作为参考，其模拟次数为1 000次。

假设各随机变量相互独立，负荷服从式（4）所示的正态分布，取测试系统的负荷值为均值，取10%为标准差，系统基准值为100 MV·A。辐照度服从式（1）所示的2参数Beta分布，光伏接入点位于系统的28号节点。

按照式（17）和（18）计算3PEM 和MCS概率潮流所得节点电压的均值和标准差的相对误差，并以此为评价的标准。

将结果绘制成直方图，如图2和图3所示。

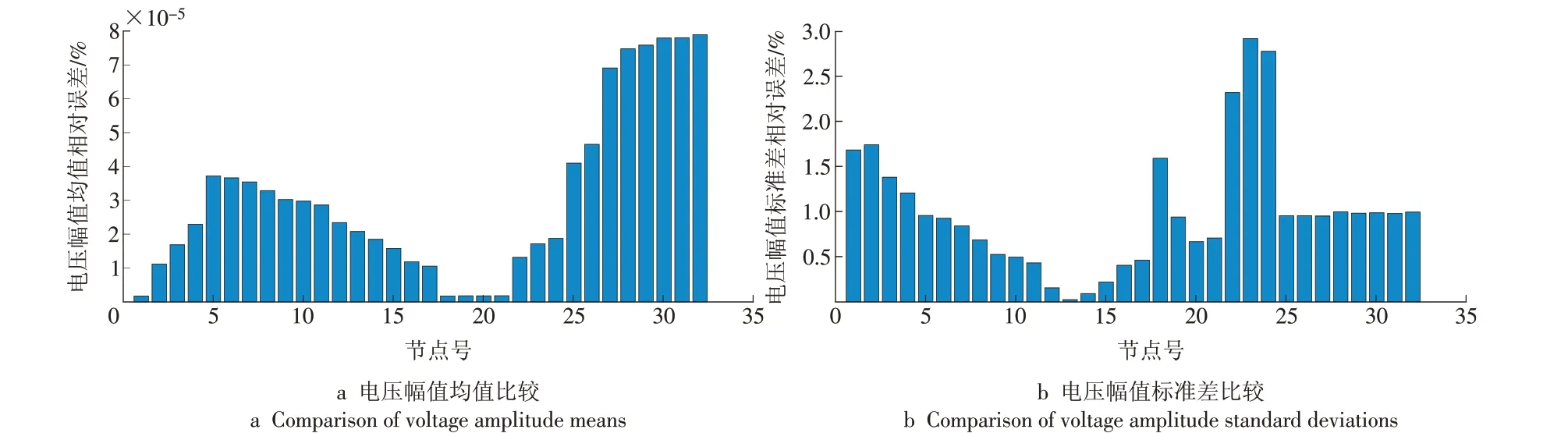
图2 3PEM和MCS电压幅值相对误差比较Fig.2 Relative error of voltage amplitudes obtained by 3PEM and MCS

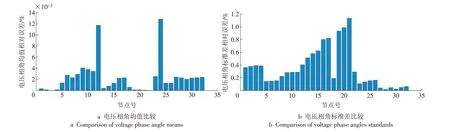
图3 3PEM和MCS电压相角相对误差比较Fig.3 Relative errors of voltage phase angles obtained by 3PEM and MCS

可以看出：各节点电压幅值的均值、标准差的相对误差最大值分别为7.89×10-7和2.92%；各节点电压相角的均值、标准差相对误差最大值分别为0.012 9%和1.14%。

由此可以说明3PEM 得到的结果准确且具有较高的精度。同时，此系统有32个随机变量，由3PEM构造出来的估计点有65 个，因此只需要进行65 次确定型潮流计算便可得出上述结果，与MCS 的1 000次相比大大减少了计算量。

因此，3PEM 非常适合应用于实际系统的概率潮流计算。

3.2.2 光伏不确定性对概率潮流的影响

3.2.2.1 对系统节点电压的影响

表1给出了在3PEM下，计及光伏与不计及光伏2个系统中各电压幅值的期望和标准差，对比2种情况下节点电压的幅值，可以观察到存在一定程度的变化。为了更清楚地表示这种变化，将计及光伏前后各节点电压幅值的均值与标准差的绝对误差绘制成图4a。从图4a 可知，距离光伏节点越近，其电压幅值的均值和标准差受光伏影响越大。

根据表1 中的数据，可画出系统各节点电压在接入光伏前后的PDF和CDF曲线。

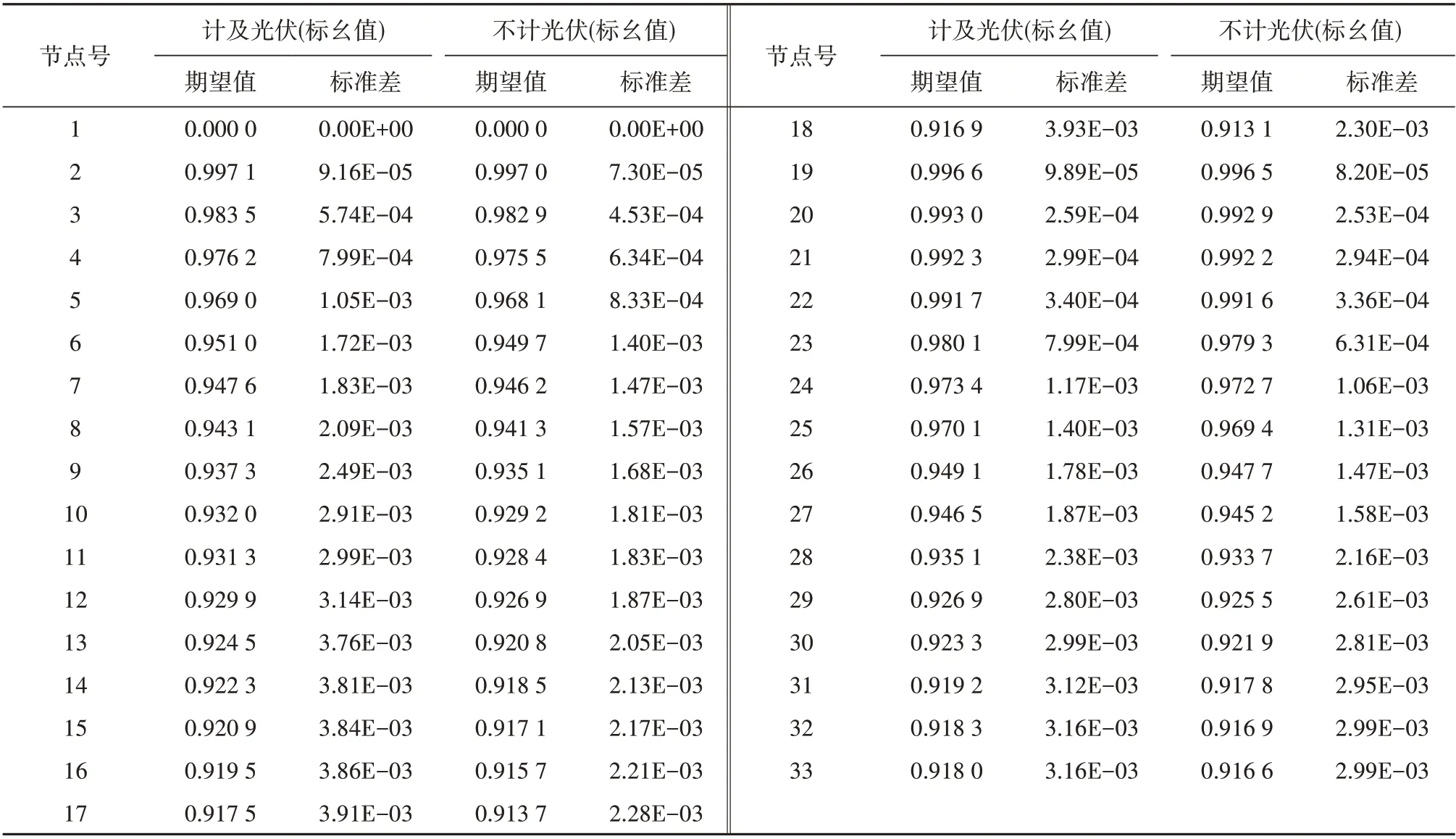
表1 计及光伏后节点电压计算结果Table 1 Results of node voltages considering PV and without PV

为了进一步研究光伏接入对系统概率潮流的影响，选择距离光伏较近的28 号节点和较远的22号节点，分别绘制其PDF 和CDF 曲线，如图5 和图6所示。

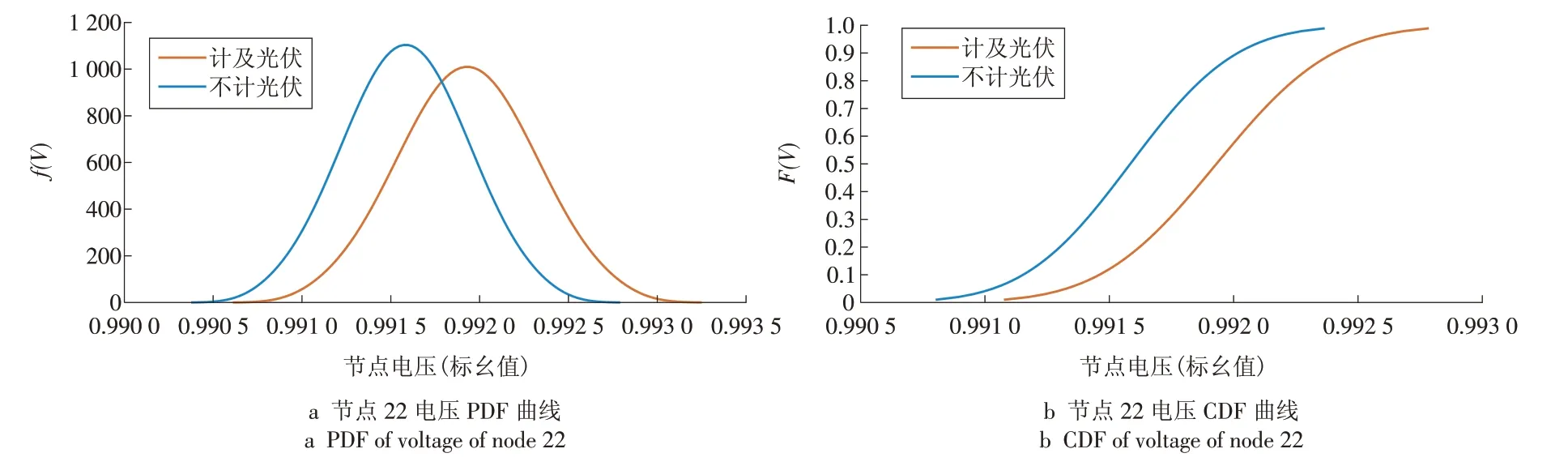
图6 计及光伏前后节点22电压的概率分布Fig.6 Probability distribution of the voltage at node 22 considering PV and without PV

由图5a所知，距离光伏较近的28号节点的电压波动非常明显。在不计及光伏的情况下，其电压均值（标幺值）为0.933 7，标准差为0.002 160；计及光伏后，电压均值（标幺值）为0.947 5，标准差为0.006 300。

从图6 可知，节点22 距离光伏较远，其PDF 和CDF 曲线在光伏接入系统前后变化不大，故其电压幅值波动幅度不大。在不计及光伏的情况下，节点22 的电压均值（标幺值）为0.991 6，标准差为0.000 336；计及光伏后，其电压均值（标幺值）为0.991 9，标准差为0.000 367。

综上所述，从图5 和图6 的概率分布曲线可知，计及光伏前后节点28 和节点22 的电压都发生右移，其中节点22 移动的程度很少，而节点28 移动的程度很明显。

3.2.2.2 对系统支路功率的影响

3PEM 下计及光伏前后系统支路有功功率的期望值和标准差见表2。

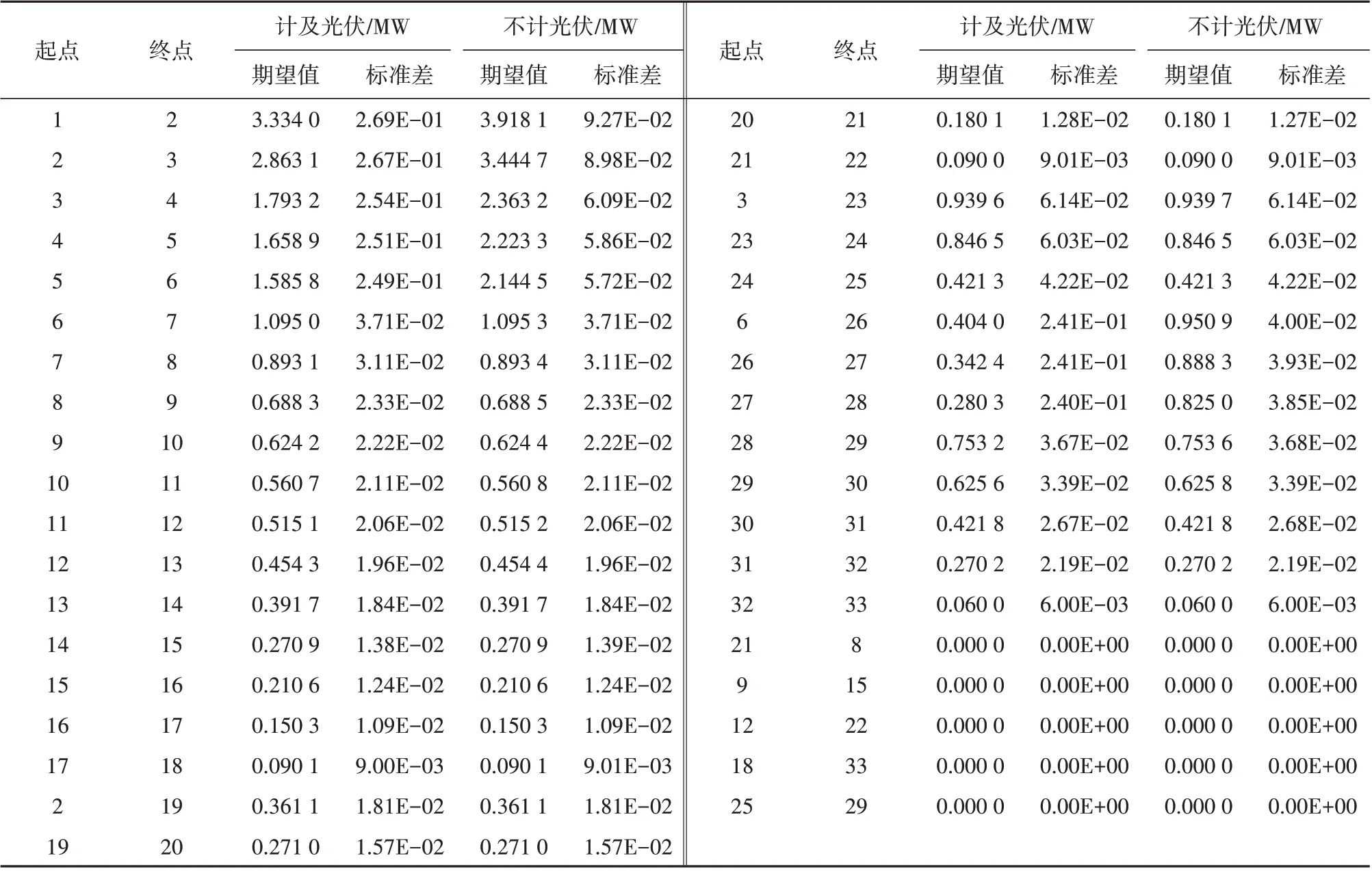
表2 计及光伏后系统的支路有功功率数据Table 2 Active power flow of each line considering PV and without PV

为了清晰地观察它们的变化，图4b绘制了计及光伏前后支路有功功率期望与标准差的绝对误差。经对比可发现，1—2，2—3，3—4，4—5，5—6 支路以及6—26，26—27，27—28 支路的有功功率有明显的改变，这些支路恰好分布在光伏附近。

取离光伏较近和较远的2 条支路，即支路27—28 和支路7—8，分别绘制它们的PDF 和CDF 曲线，如图7 和图8 所示。从图7 和图8 可以看出，支路7—8 距离光伏较远，受光伏影响较小，潮流变化不明显，而支路27—28与光伏相连，受光伏影响较大，潮流的变化明显。

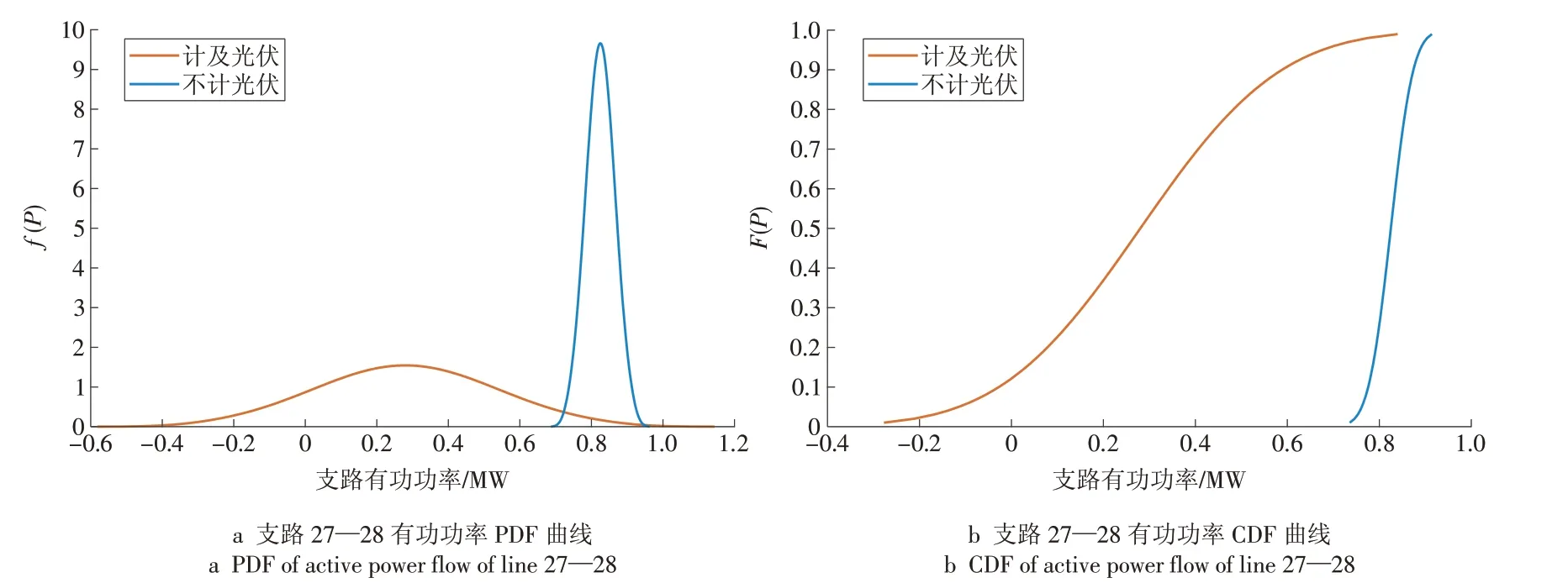
图7 计及光伏前后支路27—28有功功率的概率分布Fig.7 Probability distributions of the active power flow of line 27-28 with PV and without PV

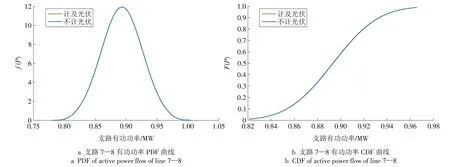
图8 计及光伏前后支路7—8有功功率的概率分布Fig.8 Probability distributions of the active power flow of line 7—8 with PV and without PV

综上所述，接入光伏后，系统的节点电压和支路潮流均受到不同程度的影响，且距离光伏接入点越近，受其影响越严重。

4 结论

本文提出了基于3PEM 的电力系统概率潮流计算方法，有效实现减少采用时间的同时确保采样样本的有效性。应用本文所提方法对考虑负荷和光伏不确定性的系统进行测试分析，与MCS 进行对比，结果表明基于三点估计的概率潮流计算结果准确且大大减少了计算量，验证了其有效性。在此基础上，进一步研究并分析了计及光伏前后对系统的影响，结果表明距离光伏接入点越近，节点电压和支路潮流的变化程度越大，但随着距离的增加，这种影响逐渐减弱。