基于EEMD-BiLSTM 的可调节负荷预测方法

李彬，胡纯瑾*，王婧

（1.华北电力大学电气与电子工程学院，北京 102206；2.国网综合能源服务集团有限公司，北京 100052）

0 引言

“双碳”目标下，加快构建以新能源为主体的新型电力系统成为必然，为有效提升电网调节能力，源荷互动电网调控模式必将替代传统的“源随荷动”。2022 年，国家发展改革委、国家能源局发布《关于完善能源绿色低碳转型体制机制和政策措施的意见》（发改能源〔2022〕206 号）［1］，提出积极推动电力需求响应市场化建设，将需求侧可调节资源纳入电力电量平衡，发挥需求侧资源削峰填谷、促进电力供需平衡和适应新能源电力运行的作用。可调节负荷作为新兴电网调节资源，能有效改善电网调节资源的局限性，实现“双碳”目标。通过市场机制创新，可调节负荷可参与电力中长期、现货、调峰、调频、备用市场等。可调节负荷参与市场涉及电网企业、用户、发电企业等的切身利益［2］，不同负荷侧调节资源间及其与传统电源侧调节资源间、与调度机构间存在市场准入、调节量计算等协调需要。

文献［3］阐述了电力负荷预测中常用的几类深度学习算法，对比分析验证得出长短期记忆（LSTM）神经网络算法具有较好的预测性能。文献［4］以卷积神经网络（CNN）与LSTM 神经网络对时间序列的较强处理能力，提出CNN-LSTM 混合神经网络模型算法，对时序性短期负荷进行预测。文献［5］在LSTM 神经网络基础上引入注意力机制，以突出对负荷预测起到关键作用的输入特征，提出基于Attention-LSTM 网络的短期负荷预测模型。文献［6］在已有的LSTM 神经网络模型和宽度&深度模型的基础上，建立Wide&Deep-LSTM 深度学习短期负荷预测模型，有效解决台区电力负荷预测的多特征维度及时序性特征问题。文献［7］提出一种经验模态分解- 堆栈式长短期记忆（Empirical Mode Decomposition-Spatial Long Short Term Memory，EMDSLSTM）组合的短期负荷预测算法，分别对分量负荷和原始负荷数据进行预测建模及其重构，结果表明经验模态分解算法虽然能有效提高模型的预测性能，但容易出现模态混叠现象，预测模型无法达到更优的准确度。文献［8］通过构建集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）及门控循环单元（GRU）神经网络和多元线性回归（MLR）组合而成的EEMD-GRU-MLR（EGM）预测方法，有效提高了电力负荷短期预测精度，但由于可调节负荷具有时间相关性，EGM 方法并不适用于可调节负荷预测。

为解决EMD 的模态混叠现象，同时获取负荷序列良好的时间感知能力，本文提出一种集合经验模态分解-双向长短期记忆（Ensemble Empirical Mode Decomposition-Bidirectional Long Short Term Memory，EEMD-BiLSTM）组合的可调节负荷预测方法，利用EEMD 将非平稳、非线性负荷分解为更具平稳的分量负荷，分别对分量负荷和原始负荷数据进行预测模型及重构，再结合BiLSTM 及其参数，利用双向循环网络使用顺序和倒序2个方向对已知序列进行学习，输出结果包含二者信息，对EEMD算法获得的分量负荷进行训练，对各分量结果进行线性叠加，得出最终值。试验结果表明，EEMD 算法能极大提高模型的预测性能，BiLSTM模型能有效提升模型的时间感知能力。

1 可调节负荷预测方法现状

可调节负荷序列是非线性且非平稳的，对于这类信号，基于小波的去噪方法已经取得过一定的效果，但这些方法必须要预先设定基函数。文献［9］提出的EMD 虽能快速应用于信号去噪，但当信号出现异常事件时，将影响极值点的选取，筛选出的本征模态函数（Intrinsic Mode Function，IMF）分量包含了信号的固有模式和异常事件或相邻特征时间尺度的固有模式，从而产生模态混叠现象。随后文献［10］对EMD 进行了改进，提出EEMD，有效抑制模态混合。

可调节负荷预测有助于提高发电和配电的效率，具有实时调度、提高电力系统可靠性、降低运行成本、影响市场收入等作用。目前国内外对提高负荷预测准确性的研究主要包括基于时间序列的各种方法：自回归移动平均（Auto Regressive Moving Average，ARMA）模型、回归模型、支持向量机（Support Vactor Regression，SVR）、模糊理论以及混合模型。传统的预测算法由于提前假设了相关时间序列的线性关系，无法处理噪声大、波动大、趋势不规则、非线性的数据等问题。在实际应用中，如果原始数据收到突然变化的社会或环境因素的影响，这些预测方法的误差都会显著增加。

浅层学习模型更适用于适应强的非线性学习和快速计算。深度学习模型可以通过增加隐藏层的数量从可调节负荷中提取深度信息。最常用的技术包括递归神经网络（Recurrent Neural Network，RNN）、CNN 和LSTM。文献［11］提出了一种具有LSTM 的循环神经网络。LSTM 克服了RNNs 的长期以来性问题，LSTM 使用单元状态、输入门、遗忘门、输出门4 部分在序列中保持长期和短期的依赖关系。然而，传统的LSTM 只提供以前的数据，它通过隐藏状态以forward 方式接受输入。为解决这个问题，提出了BiLSTM。在BiLSTM网络中，输入可以同时在2 个方向上进行处理，通过拟合2 个LSTM 的输出得到最终结果。与LSTM 相比，对于相同的输入序列，BiLSTM的预测精度更高。

1.1 EEMD方法

EMD 在分析非平稳、非线性的时间序列数据时具有自适应且高效分解的特点。根据原始数据信号的局部特征，通过EMD 技术从任何复杂信号中逐级提取不同尺度的波形或趋势，将原始序列分解为相对稳定的IMF和残差分量。各IMF必须满足以下2个条件。

（1）整个信号区间中的极值点数等于零点或差值为1。

（2）信号的平均极值为0。

EMD分解流程如图1所示。首先计算原始信号上下极值点，画出基于极值点的上下包络线，根据上下线画出均值包络线，将原始信号减去均值包络线，检查得到中间信号是否满足IMF条件，若满足则选中为IMF分量，若不满足则迭代上述步骤，经过多次迭代得到满足IMF条件的分量和1个残差值。

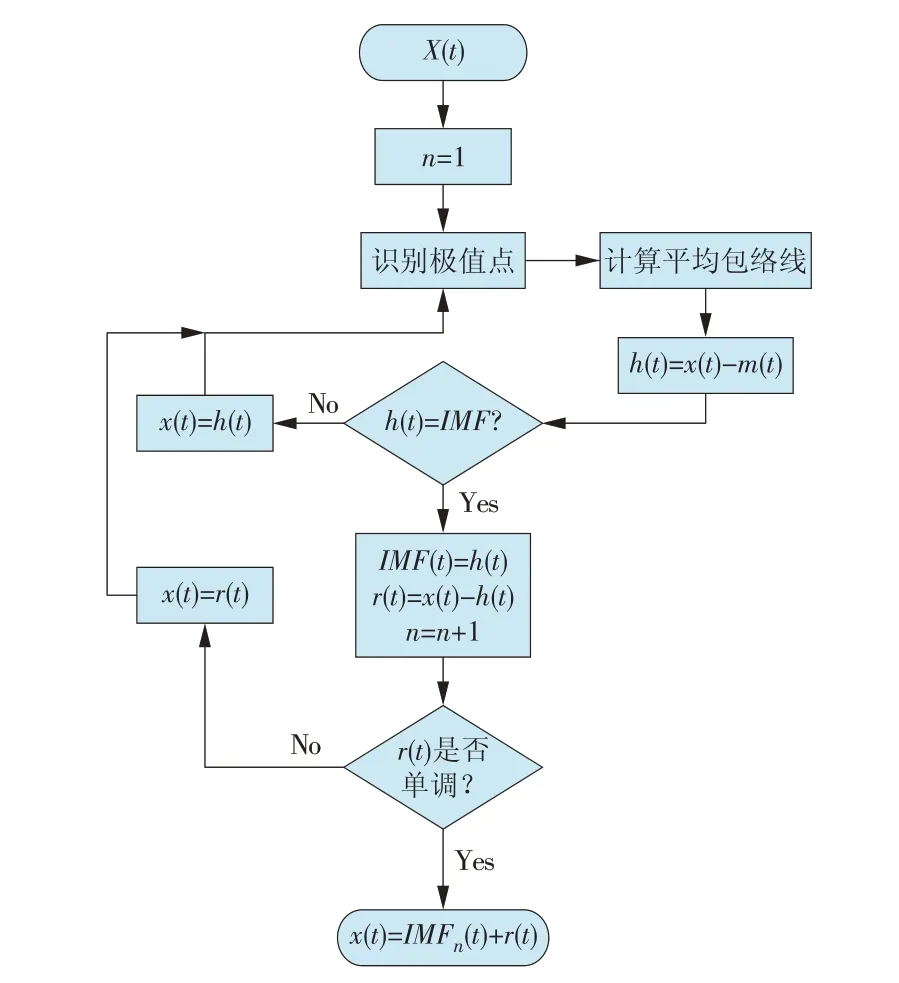
图1 EMD分解流程Fig.1 EMD decomposition

循环神经网络中输出对张量Wxh，Whh和偏置b均可导，利用自动梯度算法来求解网络的梯度，其中误差L为最终输出值ot与真实值之间的差距。

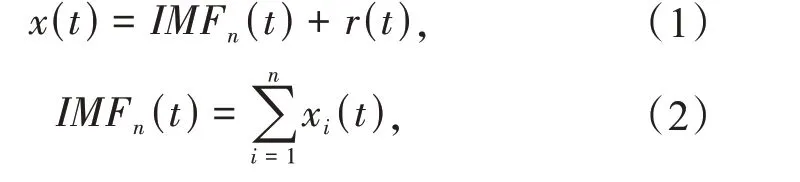
式中：x(t)为原始信号；IMFn(t)为IMF 分量；r(t)为残差分量。

对于2个局部最小值或最大值点，c(t)作为平均值为零的振荡函数，取值为零。信号分解过程的理论基础表达式为

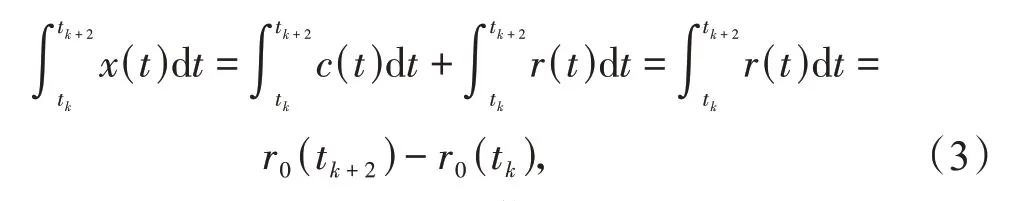
式中：x(t)为非平稳振荡信号；c(t)为振荡分量；r(t)为残差分量，r0表示过程的初始剩余。

EEMD 本质上是用给定的试验次数对原始负荷序列反复应用EMD，然后对所有分解结果取平均值。与EMD 不同，在每次EEMD 尝试中，将频率范围均匀分布的高斯白噪声加入到原序列中，使得具有噪声辅助的原始负荷序列不仅具有均匀分布特性，还具有平滑等特性。

EEMD［12］的简要步骤如下。

（1）给原始负荷序列添加1 个给定振幅的白噪声。

（2）对加入白噪声的负荷序列进行EMD 处理，得到IMF分量和剩余分量。

（3）按照给定试验次数重复步骤（1）和步骤（2），在每次试验中，IMF数量为常数。

误差的最终标准偏差为输入信号和相应IMF之间的差值，计算公式为

式中：N为IMF 分量数；A为附加噪声的振幅；ε为误差的最终标准偏差。EEMD分解流程如图2所示。

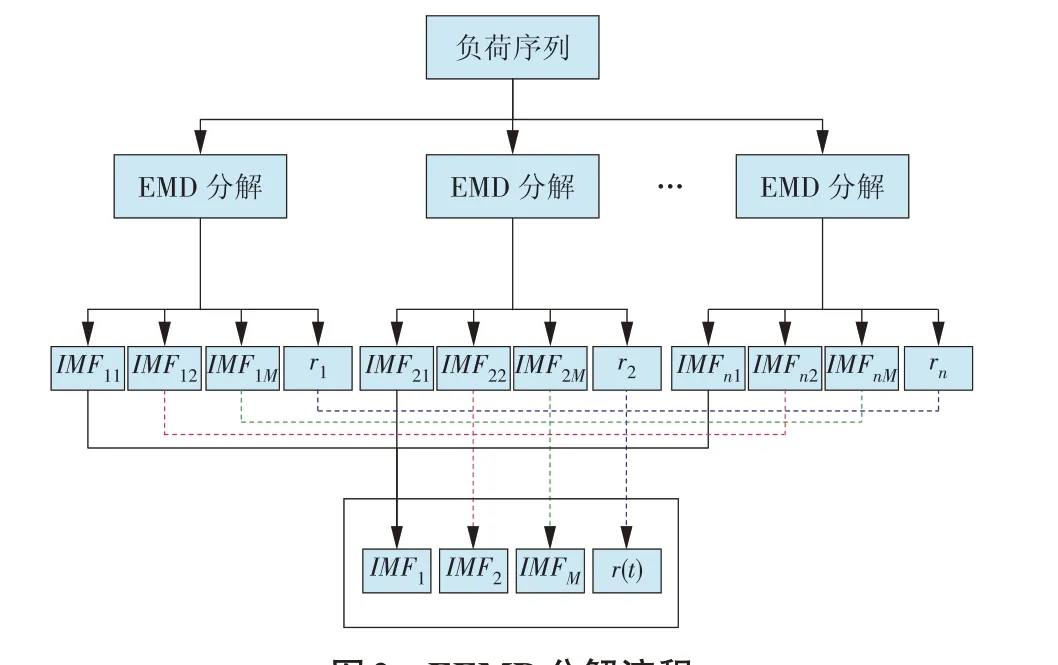
图2 EEMD分解流程Fig.2 EEMD decomposition

1.2 BiLSTM 方法

在LSTM 模型中，c为LSTM 模型的状态向量，h为LSTM 网络的输出向量，利用门控值向量σ(g)表示阀门开关程度。输入门和遗忘门的典型行为见表1。

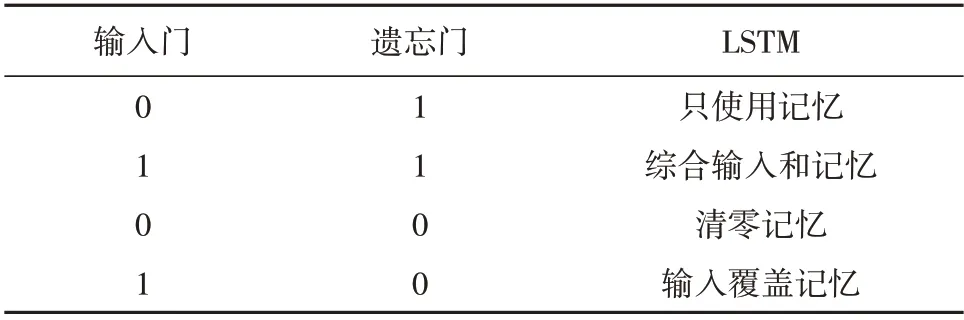
表1 输入门和遗忘门的典型行为Table 1 Typical behavior of input and forget gates

LSTM记忆细胞的运算过程为

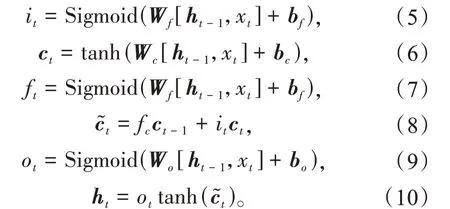
LSTM 模型虽然可以捕捉到较长距离的依赖关系，但LSTM 模型中一般将过去的信息作为输入和隐藏层，而忽略了未来信息。

BiLSTM 在LSTM 基础上，采用2 个独立的隐藏层对序列数据进行正向和反向处理，将2 个连接层连接到同一输出层，将之前的信息和之后的信息作为时间序列数据的当前时间基础。使用BiLSTM 网络进行预测，其对于连续时间序列有很好的表达能力，权重参数复用使得其对数据的要求更低。BiLSTM模型如图3所示［13］。

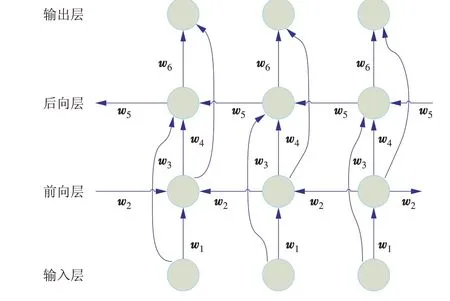
图3 BiLSTM 模型Fig.3 BiLSTM model

因此，在数据预处理阶段，针对可调节负荷序列，采用EEMD能有效解决电力负荷数据的非线性、非平稳问题，通过将具有频率范围内均匀分布的统计特性的白噪声添加到负荷序列中，使得负荷序列具有均匀的分解尺度和平滑性。在负荷预测阶段，将扁平化的数据输入BiLSTM，改善负荷序列提取时相互依存的问题。BiLSTM模型中，前向层从负荷序列的起点开始输入，反向层由数列的末端开始输入，通过多次迭代最终将2层的输出结果进行拟合，有效提高预测精度。

2 EEMD-BiLSTM可调节潜力分析改进方法

2.1 负荷序列分解流程

步骤1：添加正态分布高斯白噪声εs到原始负荷序列Y，然后输入新的负荷序列

基于高斯分布的统计特性，EEMD 方法可以有效抑制EMD 分解过程中由于IMF 的间歇性而引起的模态混合问题。由于电力负荷序列具有非线性、非平稳特性，电力负荷序列更适用于EEMD 分解处理，使用获得的子序列进行训练，得到各个训练后的结果，线性叠加后就是最终值［15］。

2.2 可调节负荷预测流程

在BiLSTM 模型中，前向层和后向层共同连接着输出层，其中包含了6个共享权值w1～w6。在前向层从时刻1～t正向计算一遍，得到并保存每个时刻向前隐含层的输出。在后向层沿着时刻t～1 反向计算一遍，得到并保存每个时刻向后隐含层的输出。最后在每个时刻结合前向层和后向层相应时刻输出的结果得到最终的输出［16］。

数学表达式为

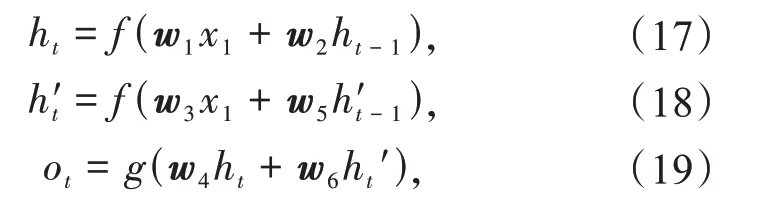
式中：x1为t时刻的输入量；ht和h′t为t时刻的前向层与后向层的输出量；ot为t时刻输出层的输出；f为前向层与后向层的激活函数；g为输出层的激活函数；w1为输入层映射到前向层的权重矩阵；w3为输入层映射到前向层的权重矩阵；w2为前向层前一时刻输出映射到当前计算时刻的权重矩阵；w5为后向层前一时刻输出映射到当前计算时刻的权重矩阵；w4为前向层的输出映射到输出层的权重矩阵；w6为后向层的输出映射到输出层的权重矩阵。

结合各方法的优势，构建EEMD-BiLSTM 可调节负荷预测模型，流程如图4所示。

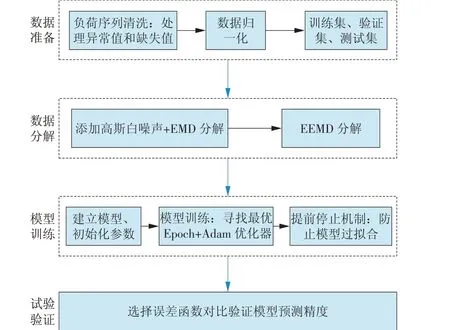
图4 基于EEMD-BiLSTM 可调节负荷预测模型流程Fig.4 Adjustable load prediction model based on EEMD-BiLSTM

选取可调节负荷数据，分析数据集是否存在异常值或缺失值等情况，针对异常值利用函数进行修补或剔除，针对异常值一般采用删除或补全法，完成可调节负荷数据的清洗。对清洗后的可调节负荷序列进行EEMD分解，将分解后的序列作为输入，建立BiLSTM 模型，初始化参数，通过模型训练寻找最优Epoch和Adam 优化器，设置提前停止机制防止模型过拟合，选择合适的误差函数对比验证预测模型结果，确认模型预测精度。

3 仿真验证

数据选取国内某地区连续5年涵盖日需求负荷的真实运行数据作为原始负荷数据集，日平均负荷曲线如图5所示，纵坐标为日平均负荷量。

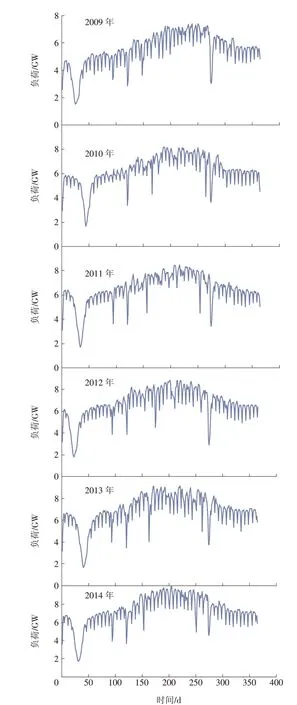
图5 2009—2014年日平均负荷曲线Fig.5 Average daily load from 2009 to 2014

观察原始负荷曲线图，发现部分日平均负荷出现极低的情况，可能是由于大停电等特殊情况或电表监测失误所形成。每年2月出现集中日平均负荷极低的情况，分析可能是2月春节放假期间，办公地区及工厂等工作区域用电量骤降。

2014年4月前后该地区的日平均负荷与其他月份相比较低，考虑到温度影响，认为4月基本没有温度敏感性负荷。

从5月开始，随着温度升高，日平均负荷曲线开始逐渐升高，温度敏感性负荷开始大量使用。至10月温度再次回归适宜，但与4月相比，日平均负荷稍有增加，考虑是由于公共区域人流量较上半年有所增加，用电负荷相应有所增长。进入冬季后，地区温度下降，温度敏感性负荷再次增长，用电量再次升高。将温度设定为23 ℃，观察温度历史数据集，发现4 月13 日温度恰好适宜，选取当日平均负荷作为基本正常负荷，将温度上升后5—9月扣除基本正常负荷，获得剩余日总负荷视作可调节负荷，如图6所示。

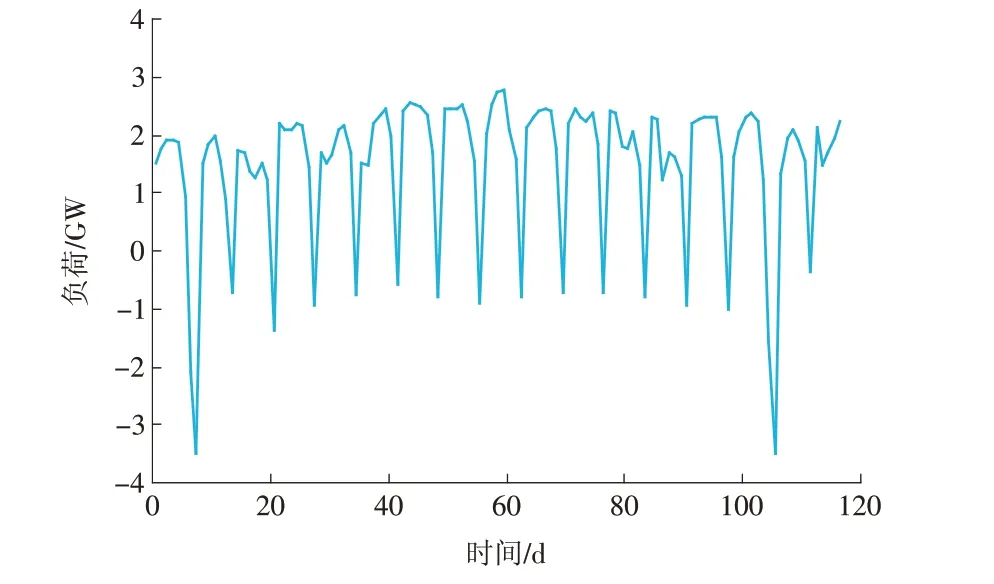
图6 2014年可调节负荷曲线Fig.6 Adjustable load curve in 2014

针对提取的可调节负荷序列，采用EEMD 方法分解得到5 个IMF 分量，将每个分量数归一化到［0，1］内，将归一化的数据作为输入，在BiLSTM 模型中进行预测，选取2009—2012年可调节负荷序列作为训练集，2013 年可调节负荷序列作为验证集，2014年可调节负荷数据作为预测集。

将预测结果反归一化后，各分量预测结果线性叠加得出预测结果，将预测结果与原始负荷数据进行对比，对比预测结果与原始负荷数据，计算参数优化的EEMD-BiLSTM 模型预测精度。

在BiLSTM 模型训练阶段，通过多次迭代得出权重的最优值，而Epoch 参数的大小与预测结果息息相关。Epoch 参数过大时，网络分类复杂，模型不仅学习到正确信息，也会从一些错误信息中学习，会造成训练结果出现过拟合现象，而Epoch 参数较小时，网络分类过于简单，模型无法学习到正确信息，会造成训练结果出现欠拟合现象。选用Tensorflow-keras 库中的EarlyStoping 函数，提前停止机制防止过拟合现象［17］。

当网络模型层数较深时，Sigmoid 函数容易出现梯度弥散现象，导致预测精度下降，而ReLU 函数在x＜0 时梯度值恒为0，容易出现梯度弥散现象，因此针对可调节负荷序列，选取tanh 函数作为激活函数，Adam 作为模型优化器搭建训练环境。将参数优化后的EEMD-BiLSTM 模型与LSTM 模型、EEMD-LSTM 模型和BiLSTM 模型选用误差函数平均绝对误差（MAE）、均方根误差（RMSE）对预测结果进行评估。可调节预测负荷曲线对比情况如图7所示。

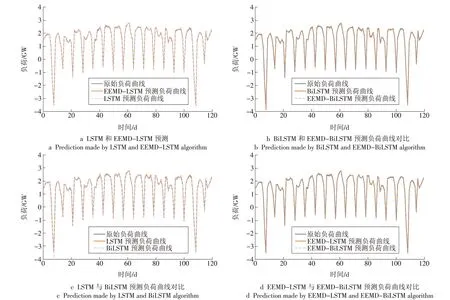
图7 可调节预测负荷曲线对比Fig.7 Comparison of adjustable load prediction curve

各模型评价指标对比见表2。观察曲线图及其误差函数可知，加入高斯白噪声后，运用EEMD分解方法对原始可调节负荷序列进行分解，EEMDLSTM 模型预测精度高于LSTM 模型，EEMDBiLSTM模型预测精度高于BiLSTM模型。

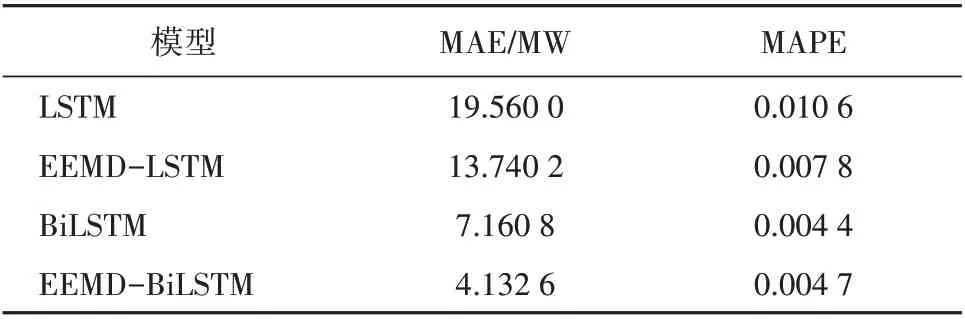
表2 各模型预测情况对比Table 2 Comparison of prediction made by different model

此外，观察对比图7 可知，BiLSTM 模型预测精度高于LSTM 模型，EEMD-BiLSTM 模型预测精度高于BiLSTM 模型，BiLSTM 模型具有更优秀的时间序列感知力，能够从训练集中提取更多的有效信息进而提高预测精度，与BiLSTM 模型相比，LSTM 模型稍有滞后效应。EEMD-BiLSTM 模型不仅具有良好的时间序列感知力，可以从较长训练集中提取更多有效信息以提高预测精度，在面对较长训练集时，EEMD 有效降低了尺度混合对分解的影响，提高了模型的预测精度。

4 结论

本文分析了EEMD和BiLSTM算法的原理，提出了EEMD-BiLSTM 模型应用到可调节负荷预测中。对预处理后的可调负荷进行EEMD 分解，试验设计了BiLSTM 架构及其参数，分别对分量负荷和原始负荷进行训练和重构预测。试验结果表明，EEMD分解算法能有效规避EMD 分解算法中的模态混叠问题，有效提高模型的预测性能。同时，基于BiLSTM 的学习方法可以将过去和未来的数据序列统一为输入值，考虑数据的反向关系，有效预测可调节负荷序列的动态趋势。由于在LSTM 的基础上增加了反向结构，BiLSTM模型明显延长了模型的训练时间，降低了运算速度。因此在选择预测模型时，应权衡模型的训练效率和预测精度，选择更适合的训练模型。