二阶下三角矩阵代数的左理想共轭类*
2022-09-28高凤霞杨瑞芳
高凤霞,杨瑞芳
(1.河南工学院 理学部,河南 新乡 453003;2.山西师范大学 数学与计算机科学学院,山西 太原 030032)
0 引言
设A是一个含有单位元的有限维的结合代数,L(A)为A中所有左理想组成的集合,U(A)为A的单位群。在集合L(A)中可定义等价关系~:L1~L2当且仅当存在u∈U(A)使得u-1L1u=L1u=L2。对任意I∈L(A),称子集[I]={L|L~I,L∈L(A)}为L(A)的一个等价类(共轭类),L(A)的所有等价类作成的集合记为C(A)。由左理想的乘积亦是左理想可知C(A)有一个自然的半群结构:即对任意1,[L1][L2]=[L1L2],以下简称A的共轭类半群(关于共轭类半群更详细的知识可参阅文献[1]),其有限性和A的表示类型密切相关[2,3]。此外,C(A)也和结合代数的子空间半群有着密切的关系[4,5]。
本文的主要目标就是对典型有限维代数——二阶下三角矩阵代数刻画其共轭类半群的乘法结构。
1 定义与定理
本文中C表示复数域。文中出现的代数、向量空间、基等均定义在C上,有关矩阵的基本概念和知识可参阅文献[6]。
定义1[6]设A是一个代数,e∈A。若e2=e,则称e为A的一个幂等元。若幂等元e1,e2满足e1e2=e2e1=0, 则称e1,e2是正交的。
若非零幂等元e不能表示两个非零正交幂等元的和,则称e是本原的。设{e1,e2,…,en}为A中本原正交幂等元的集合,若e1+…+en=1,则称{e1,e2,…,en}为A的本原幂等元的完全集。
定义2[7]设I是A的一个左理想,若存在正整数m使得Im=0,
则称I是A的一个幂零左理想,称A的最大的幂零左理想为A的贾柯波逊根,记为rad(A)。
定义3[7]设I是A的一个左理想,若I不能表示为两个非零左理想的和,则称I是不可分解的。
引理1[7]若{e1,e2,…,em},{f1,f2,…,fn}为A的两组本原正交幂等元的完全集,则m=n,且存在a∈U(A)使得经过适当的重排下标后对于1≤i≤n均有fi=aeia-1。
引理2[7]设e,f为A的幂等元,则[Ae]=[Af]当且仅当存在a∈U(A)使得f=aea-1。
引理3[8]设Li∈L(A),i=1,2, 则存在幂等元ei∈Li使得:
(1)Li=Aei⨁Li(1-ei),Li(1-ei)⊆rad(A),i=1,2;
(2)[L1]=[L2]当且仅当[Ae1]=[Ae2],[L1(1-e1)]=[L2(1-e2)]。
在下文中我们恒使用以下符号:
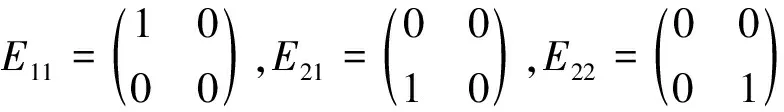
类似于文献[9]中关于一般矩阵弱相似的概念,本文给出下三角矩阵弱相似的概念。
定义3设B1,B2∈T,若存在P∈G,α∈C*,使得PB1P-1=αB2,则称B1与B2在T中弱相似。易知弱相似是T上的一个等价关系。
定理1 中元素的弱相似等价类刚好有三个。其代表元如下
2 主要结果
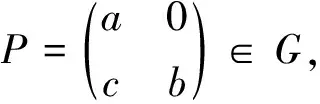
定理2T中不可分解的左理想共轭类和X中元素的弱相似等价类一一对应。
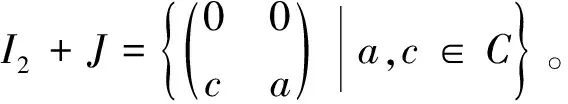
可得I1I2=0,I1J=0,I1(I2+J)=0,I1I1和I1T均有基E11,E21,即I1I1=I1T=I1。同理可得
I2I1=I2J=J,
I2T=I2(I2+J)=I2+J,
I2I2=I2,JI1=JT=J,
JJ=JI2=J(I2+J)=0,
(I2+J)I2=I2,
(I2+J)T=(I2+J)(I2+J)=I2+J,
(I2+J)I1=(I2+J)J=J。
此外,对任意的左理想I恒有TI=I。
设e=[T],
α1=[I1],
α2=[I2],
β=[J],
γ=[I2+J],可得
定理3C(T)={0,e,α1,α2,β,γ}其乘法表见表1。

表1 的乘法表
