基于均值-MF-X-DMA的能源产业链投资组合策略

陈洪涛 ,昝秋雨 ,王 锋 ,叶 鑫

(1.东南大学 经济管理学院,南京 211189;2.东南大学 国家发展与政策研究院,南京 211189;3.中国矿业大学 经济管理学院,江苏 徐州 221116)

在过去的几十年中,全球能源商品市场及其衍生品市场保持快速增长,已成为各种基金及对冲、套利和投机活动的重要投资对象。鉴于巨大的资金需求和较长的回收期,能源投资向来存在着极高的不确定性。近年来,气候变化、经济周期的波动、金融市场的不稳定性以及地缘政治的不确定性等因素加剧了能源价格的波动,国际油价的剧烈波动印证了能源金融投资的复杂性。美国能源企业与市场接轨程度较高,金融市场也相对成熟,能源股对于市场信号的反应灵敏,自2020年4月20日,美国WTI原油期货首次收跌为负后,两年间从负37.63美元上涨至130.5美元,最高涨幅超过446.8%。相比之下,中国能源供应企业垄断程度较高,国际突发事件对于中国能源股票市场的冲击较小[1]。能源作为重要的战略储备,其投资组合的优化不仅是为了实现预期收益最大化和风险最小化,还是为了保障相关产业的正常运转和国家安全。

随着《外商投资准入特别管理措施(负面清单)(2021年版)》等系列政策的出台、“一带一路”能源合作伙伴关系的确立,中国能源市场与国际接轨程度逐步提升。在能源产业布局方面,中国能源以进口为主,能源市场的开放程度逐年提高。截至2021年底,中国原油和天然气的对外依存度分别为73%和45%。外资在中国能源市场的准入范围也逐步扩大,能源产业的国际化水平不断提升。截止2021年第三季度末,外资在中国能源板块的持股比例由2020年的0.54%上升至1.18%,实现翻倍增长。在能源市场投资方面,能源资产是中国外汇境外投资组合中的重要板块,国内证券市场与国际证券市场的相关性也不断增强。中投公司的外汇境外投资组合中美国股票高达57%,能源板块是其重要投资领域。中美经济间的关联性、股市间的联动性也在不断提升[2]。因此,本文以美国能源产业为样本,不仅有助于实现中国海外能源资产的风险管理,也有助于优化中国能源产业的投资版图。

当前,能源投资者主要通过分散投资种类和改进投资组合模型,实现对能源投资组合策略的优化。在选取能源投资种类时,投资者通常根据能源的使用现况和发展预期等因素,在不同类型的能源间分散投资,实现投资回报的稳定性[3-4]。然而,各类能源投资的不确定性普遍偏高,且能源商品间存在一定的价格波动相关性,基于不同能源种类构建的投资组合对风险的规避能力较弱。由于产业链上下游存在价格传导机制和稳定机制,基于产业链理论构建投资组合,不仅能满足资产多元化的需求,也能提升被投资公司整体预期业绩的稳定性,从而消除相对波动风险,实现投资组合的优化。

众多学者在确定投资组合方法时基于Markowtiz提出的均值-方差投资组合模型构建能源投资组合。该模型奠定了现代投资组合方法的基础,但也存在着计算复杂以及假设严苛与实际金融环境不符的局限性。已有学者通过简化计算并放宽假设条件优化了该模型,但并未突破有效市场假说的核心理念。其所假定的不存在任何信息摩擦的完全竞争市场与实际环境冲突,难以解释真实金融市场中存在的资产价格波动的长程相关性、收益率的“尖峰厚尾”等分形特征[5-7]。考虑到金融市场的复杂性和异质性,分形市场假说拓宽了有效市场假说的适用性。研究表明,中美股票市场及能源期货市场均具有多重分形特征,且不同的时间序列间存在多重分形相关性[8-11]。油价的波动是导致能源市场具备分形特征的主要原因,近年频繁的极端事件使得国际油价振荡剧烈,能源市场金融风险激增,中美能源市场的分形特征愈发显著[12-13]。考虑到能源资产价格波动的多重分形特征以及不同金融系统间的多重分形相关性,本文使用多重分形理论指导投资组合的构建,并细化分形市场假说的应用场景。

综上所述,首先,本文基于产业链理论的纵向整合思想,在标普500指数中选取能源上市公司,削弱能源产业链中个别公司股价波动带来的投资风险;其次,在能源金融市场存在分形特征的现实背景下,结合均值-方差模型和分形方法MF-X-DMA,构建均值-MF-X-DMA 模型;最后,制定能源投资组合策略。本文的贡献主要有:运用产业链理论分散市场风险,拓宽了产业链理论应用范围。基于分形市场假说,放宽传统投资组合理论的应用条件,丰富了现代投资组合理论。构建可以适应复杂多变、风险较高的非线性能源市场环境的模型,细化了分形理论的应用场景,为构建稳定性更好、回报率更高的投资组合提供了新的思路。

1 文献综述

1.1 分形方法及应用的相关研究

自然生态环境和真实金融市场等系统均具有复杂且非线性的特征,分形现象在自然界和社会经济生活中普遍存在[14]。1951年,R/S分析法被提出,奠定了分形研究的基础。自此,学者们相继提出了V/S 分析法、去趋势波动分析法(Detrended Fluctuation Analysis,DFA)、去趋势移动平均分析法(Detrended Moving Average Analysis,DMA)等单分形方法描述单个时间序列的分形特征。V/S分析法克服了R/S分析法无法计量短记忆性的缺陷,但仍存在仅适用于平稳序列的局限。DFA 和DMA 则分别通过多项式和移动平均函数来拟合消除序列的局部趋势,从而分析非平稳时间序列的长程相关性。相比于DFA,DMA 提升了精确度且减少了计算量,在应用时更具优势[15]。

单分形方法难以精确刻画时间序列的局部波动特征,而多重分形理论的应用则能突破该局限。基于DFA和DMA,文献[16-17]中提出了多重分形去趋势波动分析法(Multifractal Detrended Fluctuation Analysis,MF-DFA)和多重分形去趋势移动平均分析法(Multifractal Detrended Moving Average Analysis,MF-DMA)。MF-DMA通过减去局部均值消除局部趋势,放宽了在估计非平稳时间序列相关性时的假设,相比于MF-DFA更易实现。

单分形和多重分形方法适用于对单个时间序列的分析。然而,现实中,各个系统间往往并不独立,存在一定的互相关性。Podobnik 等[16]基于DFA提出了去趋势互相关分析法(Detrended Cross-Correlation Analysis,DCCA),用以分析两个非平稳序列间的长期互相关关系。在DCCA 的基础上,Zhou[17]结合MF-DFA 提出了多重分形去趋势互相关分析法(Multifractal Detrended Cross-Correlation Analysis,MF-DCCA),描述在不同时间尺度、不同波动幅度下,单个资产价格的波动以及不同资产价格间相关性的多重分形特征。基于此,演变出非对称多重分形去趋势互相关分析法(Asymmetric Multifractal Detrended Cross-Correlation Analysis,MF-ADCCA)和时滞去趋势互相关分析法(Time-Delay DCCA),以分析相关性不对称特征和传导效应[18-19]。然而,由于上述方法均以采用多项式拟合的MF-DFA 为基础,计算过程可能会完全消除固有趋势和多项式趋势,而无法消除内在趋势,影响结果的准确性[20],故已有研究以DCCA 为基础,提出了MF-X-DFA 和MF-X-DMA,并验证了后者相比前者在消除局部趋势上存在明显优势[21]。本质上,前述方法均基于最小二乘法进行趋势拟合,故存在消除趋势的过程。对具备多个突变点的时间序列进行趋势拟合时,基于经验模态分解(Empirical Mode Decomposition,EMD)的EMDMF-DFA、EMD-MF-DCCA 等则更为适用[22]。

随着分形理论的不断成熟以及分形方法的日趋完善,众多学者将分形理论拓展至金融市场的研究。针对不同的研究对象,金融时间序列具备多重分形特征的成因存在一定的差异性[23]。中美股票市场产生多重分形特征的主要原因是极端事件和收益率序列的厚尾分布,美国股票市场的多重分形特征还与长程相关性有关[24]。除此以外,石油价格波动也是造成中国能源类股票收益率和波动率具备明显多重分形特征的重要因素,而长程相关性只与收益率序列的多重分形特征有关[11]。

考虑到金融市场普遍存在分形特征,分形理论也被广泛引入投资组合优化研究。研究发现,相比于传统投资组合,单分形和多重分形投资组合均能通过改善盈利能力、弱化风险和获取超额收益而优化资产配置[25]。分形投资组合通过纳入时变参数、优化期望和方差等的构建方法,衡量不同时间尺度下的投资绩效,并提高了投资组合模型的风险可测度[26-28]。Li等[28]将分形方法嵌入均值-方差准则,构建了Mean-DCCA 和Mean-MF-DCCA 模型,并应用于沪港股市。曹广喜等[29]将EMD 去噪法与MF-DCCA相结合,以加密货币为投资对象,验证了该投资策略相较于传统和未去噪的投资组合有更好的盈利水平和抗风险能力。许林等[30]引入交叉相关性和非对称性概念,修正了MF-DCCA 模型,并发现中国股市与美国、英国等国家的股市间均存在具有多重分形特征的非对称相关性,证实风险在全球股市间存在传染效应。

1.2 产业链相关研究

产业链思想起源于《国富论》中提出的社会分工理论,由于视角的不同,学者们并未对产业链形成统一的定义,但就产业链上下游企业间存在的技术经济关联和逻辑关系,多数学者已达成共识[31]。同一链条中的公司通过信息传递、价值交换和价格传导,构筑紧密关系[32-33]。

产业链的运作机制使不同要素在各个环节间得以传递。上下游产业间存在着成本推动型和需求拉动型的双向价格传导关系,产生纵向链条间的价格溢出效应[34]。基于成本推动的视角,上游企业处于生产的开端,向中下游企业提供产品和服务。上游企业的收入为下游企业的成本,价格的波动会影响下游企业,实现资源传递和价值创造。基于需求拉动的视角,下游企业位于需求的终端,价格的变化传递需求信号,向上游和中游企业提供反馈,同步影响其他环节的产品价格,体现信息传递的过程[35-37]。同时,产业链的“关联效应”增强了各环节在股票市场的价格联动关系。面对经济波动等外部因素的冲击,不同环节公司的股价波动不仅会沿着产业链传导,而且会相互影响[38]。鉴于各环节间的高度关联性,产业链的纵向整合成为了学者研究的热门话题。产业链的纵向整合通过促进知识、技术等各类要素的流动、集聚,加强了主体间功能的耦合,发挥了协同作用[39-40]。首先,链条中的核心企业是推动产业链整合的关键因素,部分企业的技术突破将发挥“提升效应”,带动全链条的均衡发展[41];其次,考虑到环节间存在的互补关系,不同企业的融合和关联能有效推动外部交易内部化,实现风险防范和共担,带动产业集聚并优化空间布局;最后,产业链的纵向整合通过降低交易成本、规避双重加价,消除价格扭曲,提升社会整体福利,突破单个产业的价值限制[42-43]。总之,产业链中企业的协作不仅能促进自身及相关产业的发展,形成竞争优势,而且可以拉动区域经济的增长,实现系统增值[44]。

1.3 文献评述

尽管众多学者已经对分形方法及其应用、产业链理论展开了充分讨论,但现有研究仍存在不足:①分形市场研究亟需细化。分形市场理论常被应用于分析全球各个国家的股票、期货等市场的整体情况,而基于能源等细分领域的研究则有待丰富。②产业链理论的应用范围有待拓宽。多数产业链研究聚焦于公司治理层面,探讨行业间的价格传导机制以及产业集群的整合问题,鲜有研究基于金融市场投资者的视角,将产业链理论用于指导投资组合的构建。③投资组合的构建方法有待优化。较多学者基于MF-DFA 和DCCA 等分形方法修正传统投资组合模型,但前述方法存在计算量大和步骤复杂的局限,而具备高精确度和小计算量优势的MF-XDMA 方法应用范围不广。

因此,本文将分形市场理论、产业链理论与传统有效资本市场理论结合,优化能源投资组合策略。首先,利用产业链理论的价格传导机制和纵向整合思想,指导投资种类的选取,抵消投资组合样本间的相对波动风险;其次,将分形方法MF-X-DMA 与经典均值-方差模型结合,拓宽传统投资组合理论的应用范围;最后,构建均值-MF-X-DMA 模型,使模型适应复杂多变、风险较高的非线性能源市场环境,优化了传统投资组合模型,丰富了现代投资组合理论。

2 研究方法及模型构建

2.1 R/S分析法基本步骤

(1)将观测到的时间序列{xi},i=1,2,…,M划分为A个长度为N(2≤N≤L)的相邻子序列,其中L为子序列的最大长度,且AN=M,将第a个子序列记为Ia,a=1,2,…,A,将第a个子序列上的第k个观测值记为xk,a,k=1,2,…,N,令第a个子序列的均值为

(2)令Xk,a为子序列Ia上的累积离差,则

(3)令RIa为子序列Ia上的累积离差的极差,则

(4)令SIa为子序列Ia的标准差,则

(5)计算第a个子序列的重标极差:

(6)计算序列长度为N时,有A个子序列的R/S的均值为

(7)每一个N都有对应的(R/S)N,根据幂律关系可得

式中,a是常数。

(8)因为(R/S)N和N H成正比,将上式两边都取对数后可得

用最小二乘法拟合log(N)和log((R/S)N)的散点图,拟合直线的斜率就是Hurst指数,并由此求出分形维D,两者关系为:D=2-H。分形维是分形市场理论中重要的参数,可以描述时间序列的波动程度,是对具有复杂特征的分形体进行定量刻画的重要参数,当分形体复杂程度越高,其分形维就越大。因此,当一个收益率序列的Hurst指数越小时,分形维D越大,收益率序列的波动就越剧烈,其风险就越大。Hurst指数和分形维对风险的具体度量标准如下:

(1)当0＜H＜0.5,1.5＜D＜2时,表示一个均指回复型的时间序列,即当序列在过去是呈现上升/下降的趋势时,在未来会出现下降/上升的趋势。且时间序列波动平缓,序列遵从“有偏的随机游走”,会产生一条比随机游走更平滑的线。

(2)当0.5＜H＜1,1＜D＜2时,表示一个持久性的序列,当序列在过去呈现出上升/下降的趋势时,在未来会继续呈现出上升/下降的趋势,且时间序列波动比随机游走更加剧烈,会产生一条比随机游走更参差不齐的线。

(3)当H=0.5,D=1.5时,表示时间序列是一个随机游走的序列。

(4)当H=1,D=1时,此时时间序列是一条直线,便于对未来预测。

2.2 MF-X-DMA方法步骤

去趋势移动平均互相关分析法(MF-X-DMA)用于研究两个非平稳时间序列在不同时间标度下的非线性关系,适用于检验非平稳时间序列的相关性。其具体步骤如下:

设两个时间序列分别为{xk}和{yk},k=1,2,…,N,N为序列的长度。

(1)计算两个原始时间序列的累积离差序列:

(2)计算加权移动平均函数:

式中:Z∈{X,Y};x是不大于x的最大整数,x是不小于x的最小整数;n为窗口长度。θ∈(0,1)是参数,当θ=0时,表示向后移动平均法,此时移动平均函数包含了t时刻之前n-1个时刻的信息;当θ=0.5时,表示中心移动平均法,此时包含了t时刻之前(n-1)/2 个时刻和之后(n-1)/2 个时刻的信息;当θ=1时,表示向前移动平均法,此时包含了t时刻之后n-1个时刻的信息。通过已知多分形测度的数值试验,检验了当θ取不同值时,MF-DMA 方法对真实值的拟和效果。结果表明,当θ=0时,MF-DFA 方法对多重分形谱和标度指数τ(q)有着更准确的估计,故选择向后移动平均法计算移动平均函数

在原始的DMA 方法中,移动平均函数的计算用的是简单的移动平均法,即对移动窗口中每一个值赋予相同的权重,但是在一个系统中每一个值产生的影响都不同,距离t时刻越近的值会产生更大的影响,故选择加权向后移动平均计算,即

式中,λ=n/(n+1),n为移动平均窗口长度,n≤由于λ＜1,通过阶数的增加,使得先前数据点产生的贡献指数级减小。

(3)进行去趋势处理得到两个序列的残差序列,分别为:

(4)将两个残差序列分解为:Ns=[N/s]个互不重叠的子区间,标度s的大小和移动窗口n大小相等时能取得最好的效果。为了充分利用所有的数据信息,将该分解过程从尾到头重新进行一次,共得到2Ns个子区间,令第v个子区间分别为XXn(t)和YYn(t),其中:v=1,2,…,2Ns;t=1,2,…,s。

(5)计算每个标度s下的去趋势协方差:

式中,t=1,2,…,s。

(6)计算q阶波动函数:

(7)根据波动函数Fq(s)和标度s之间的幂律关系Fq(s)∝s Hxy(q),通过两边取对数可得

式中,c是常数。

再使用最小二乘法可得在不同q阶下的Hurst指数Hxy(q),称为广义Hurst指数。当q＞0时,Hxy(q)描述的是大幅波动的标度行为;当q＜0时,Hxy(q)描述的是小幅波动的标度行为。当序列{xk}和{yk}相同时,MF-DCCA 退化为去趋势多重分形波动分析法(MF-DMA),此时,Hxy(q)就是单个序列的广义Hurst指数。当Hxy(q)独立于q是一个常数时,序列是一个单分形过程;当Hxy(q)依赖于q时,序列具有多重分形特征。

2.3 均值-MF-X-DMA模型构建

2.3.1 均值-方差模型 假设有n种证券,wi表示投资组合中第i种证券的投资比例,ui和σi分别为第i种证券的均值和标准差为第i、j种证券之间的协方差,则在不允许卖空的情况下,马科维兹均值-方差模型可表示为:

式中,u0为期望收益。而对于投资者而言,收益率高于期望收益率的部分并不算风险,收益率小于期望收益率的部分是真正的风险,方差衡量的是所有收益的波动大小,对正的收益和负的收益同等对待,会高估了真正的风险。因此,马科维兹提出了半方差来衡量风险。令

则由期望收益率ui确定的投资组合半协方差矩阵为

从而均值-半方差模型为:

2.3.2 均值-MF-X-DMA 模型 将均值-半方差模型和MF-DMA 方法相结合构建如下均值-MF-XDMA 模型:

3 实证分析

3.1 数据选择与说明

基于产业链投资方法[39],本文选取能源投资种类的思路如下:

(1)界定能源产业链的组成环节。传统分类方式通常根据原料供给、生产过程和产品需求3个核心要素,将能源产业链划分为上游、中游和下游3个环节。考虑到能源产业具有极强的关联属性,上下游链条间的紧密关系可能会导致公司业绩的同向变动,不利于风险的规避。因此,为减少上游环节中能源专用性可能造成的影响,在不破坏链条连贯性和完整性的同时,本文将能源产业链进行上下游的双向延伸,拓展至5个环节。具体而言,将上游环节从原料的探勘与生产延伸至能源类基础设施建设领域,将下游环节从面向用能企业的炼制与销售拓展至面向个人消费者的终端领域,深度挖掘能源产出的经济价值。考虑到能源是重要的生产要素,支撑着经济社会全方面的发展,能源产业链终端环节的涉及范围较广,可细分为消费、金融、信息技术、房地产、公共事业等多个行业。在选取终端环节时,为贴合当前背景下经济增长的主要驱动因素,选择消费行业和信息技术行业为终端环节的代表,并选取相关领域的龙头企业——亚马逊和谷歌作为反映个体能源消费的样本公司。综上所述,结合Wind行业分类方法,本文将能源产业链具体划分为设备与服务、探勘与生产、储存与运输、炼制与销售以及终端5个环节。

(2)确定能源产业链的各个环节在投资组合中的权重。为抵消上下游行业间的相对波动风险,赋予每个环节相同投资比例,在各环节分别选取两支股票作为代表。

(3)选取具有行业代表性的公司。为了强调该项投资的“行业属性”而非“公司属性”,样本公司的主营业务必须具备明显的行业特征和突出的盈利水平。同时,为强化上下游行业间相对风险的抵消效应,确保各样本企业的体量相当。

因此,本文将能源产业链划分为设备与服务、探勘与生产、储存与运输、炼制与销售以及终端5个环节,并在标普500指数中,分别选取每个环节最具代表性的两支股票,共10支股票作为样本股,具体情况如表1所示。样本区间为2013年11月18日至2020年1月7日,共记1 500个交易日。数据均来自万得数据库(Wind)。

3.2 分形特征检验

3.2.1 正态性检验 收益率序列符合正态分布,是有效市场假说成立的前提条件,因此,通过对收益率序列分布特征的检验,判断适用样本股的假说。首先,根据描述性统计(见表1)可知,在偏度上,马拉松原油、瓦莱罗能源和亚马逊收益率序列的偏度大于0,呈现右偏分布特征,而其余各股收益率均小于0,呈左偏分布。在峰度上,样本股收益率序列的峰度均显著大于3,说明其不服从正态分布。其次,通过Quantile-Quantile图进行正态性检验。由于样本股较多,此处仅以哈利伯顿和斯伦贝谢两支样本股为例。如图1所示,图像均呈现右上趋势,且两端与正态分布的标准值存在一定差距,说明该两组收益率序列不仅未服从正态分布,且具备明显的“尖峰厚尾”特征,在其他样本股的检验中也得到了相似的结果。最后,通过Jarque-Bera检验进一步分析收益率序列的分布特征。J-B检验的统计量为

式中,S和K分别为序列的偏度和峰度。

如表1所示,样本股的J-B 检验,在1%的显著性水平下拒绝了收益率服从正态分布的原假设。基于上述检验发现,能源股票的收益率序列不服从正态分布,且存在明显的分形特征,因此,在构建能源投资组合时,分形市场假说相较于有效市场假说更为适用。

3.2.2 R/S分析 R/S分析法是检验收益率序列分形特征的重要方法。首先,根据样本的大小,确定n的范围为6～N/4,其中N为序列长度,图2所示为样本股log(N)、log[(R/S)n]散点图和拟合直线。其次,结合表1可知,所选能源公司股票收益率序列的Hurst指数均不等于0.5。这说明,能源股票市场是复杂的分形系统,收益率序列并非随机游走,而是呈现出明显的持续性或反持续性特征。最后,通过确定样本股的非循环周期,进一步分析持续性或反持续性特征的强度。非循环周期指标通过绘制V统计量和log(N)曲线图确定。以哈利伯顿为例,由图3显示,样本股V统计量值的走势整体向上,且存在明显的断点,在临界点处对应的N=320,说明其循环周期较大,持久性较强,其他样本股的检验结果也存在类似特征。

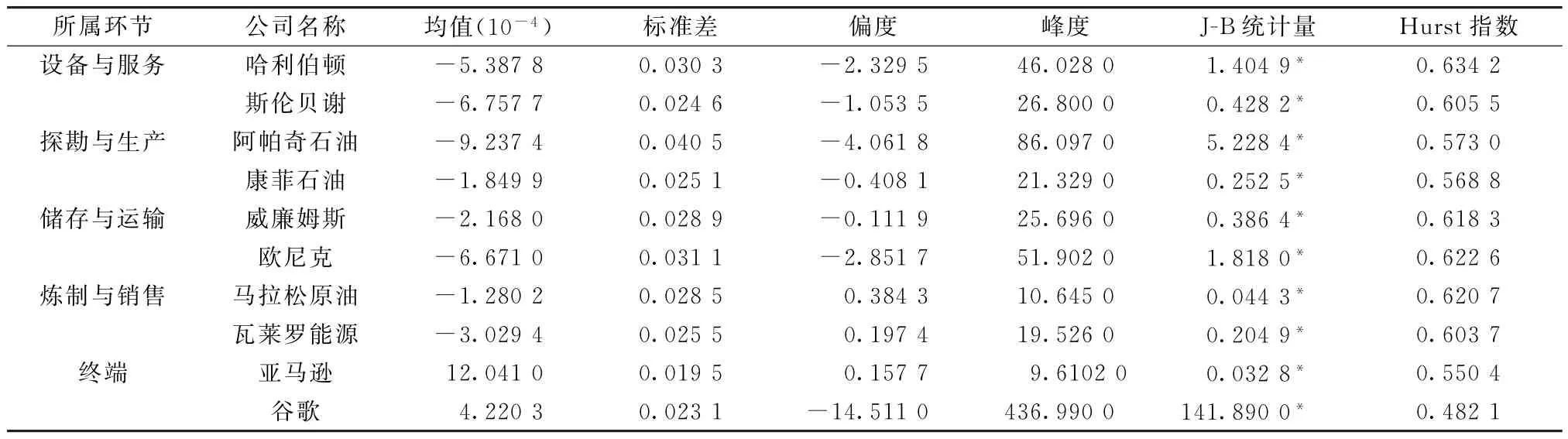
表1 样本股票收益率描述统计

3.2 多重分形特征分析

采用MF-DMA 对样本股的多重分形特征进行检验。由于样本股众多,故仅给出两支样本股的检验结果,如图4和表2所示,其中阶数q的范围为-5～5。

由图4可知,对于不同的阶数q,各样本股之间的log(Fq(x))和log(x)呈线性关系,说明各样本股收益率均存在幂律相关性。根据表2可知,随着阶数q的变化,所选样本股的广义Hurst指数也随之变化,说明两支股票均存在多重分形特征。此外,一支股票的波动会在不同的时间标度下影响另一支股票,即所选样本股之间的相关性也存在多重分形特征。综上所述,能源产业链股票市场是一个复杂的非线性系统,难以用有效市场理论准确描述市场波动,因此,基于分形市场假说构建投资组合策略较为适用。

3.3 投资组合样本外检验方法

样本外检验方法有利于评价投资组合效果。本文基于滑动窗口技术,进行样本外投资组合效果检验并比较分析。将总样本划分为估计样本和预测样本,根据文献[27]中的做法,估计样本数量通常大于总样本的80%。本文的估计样本包含1 500个交易日,预测样本包含300个交易日。具体步骤如下:

(1)将第1～1 500 个交易日(2013-11-18～2020-01-07,共1 500个交易日)作为第1个估计样本区间。根据该区间求出投资组合风险最小的资产配置方案,并按照该配置方案构建第1 501个交易日(2020-01-08)的投资组合。

(2)将第2～1 501 个交易日(2013-11-19～2020-01-08,共1 500个交易日)作为第2个估计样本区间,根据此样本区间求出投资组合风险最小的资产配置方案,并利用该配置方案得到第1 502个交易日(2020-01-09)的投资组合。以此类推,以第i(i＞1 500)个交易日前的1 500个交易日作为估计样本区间,根据该区间调整第i个交易日的投资组合权重,最终进行了300 次调整,得到预测区间300个交易日的最佳投资组合配置方案。

在对照指标的选取上,本文基于收益率、标准差、贝塔系数、夏普比率、詹森指数和特雷诺指数,对于投资组合的风险与收益进行样本外检验。在对照组的选择上,一是基于标普500能源指数,比较能源投资组合的选股方式。该指数由标普500指数中的能源公司组成,采用流通市值加权的方法构建,对于能源行业具有一定的代表性,是能源投资的重要标的。二是针对上述样本股,基于传统投资组合模型,包括均值-方差模型、等权重模型、均值-VaR 模型和均值-CVaR 模型,比较能源投资组合的模型应用。检验结果如表3、4所示。

表3 传统投资组合模型的样本外检验结果

表4 各标度下均值-MF-X-DMA模型的样本外检验结果

由表3、4的对比可得:

(1)基于收益率衡量投资组合的整体盈利能力。结果显示,标普500能源指数的收益率低于所有传统投资组合模型。产业链选股思路通过对产业链条的拓展,深度挖掘了行业价值。同时,除了标度为10之外,其余标度下的均值-MF-X-DMA 模型均能取得比传统投资组合模型更高的收益率。均值-MF-X-DMA 模型能更准确地描述各资产在不同标度下的波动情况,并使用下半收益的波动函数计算风险,衡量投资者真正关心的风险,提高投资组合的盈利能力。

(2)基于标准差衡量投资组合的整体风险。结果显示,标普500能源指数的风险大于除等权重模型外的所有传统投资组合模型。产业链选股思路能够通过平均分布各环节的投资,削弱部分环节波动对整体投资收益的影响。然而,只有两个标度下(s=150,s=200)的均值-MF-X-DMA 模型能优于全部的传统投资组合模型。这是由于均值-MF-XDMA 模型为保证投资组合的高收益率,忽视了高收益率资产的风险性,导致此类资产比重过高,增加了投资组合的整体风险。

(3)基于贝塔系数衡量投资组合相对于市场指数的波动性。结果显示,标普500能源指数的贝塔系数最小。标普500能源指数是标普500指数的子板块,不仅具有能源行业属性,还具有证券市场属性,因此系统性风险更低。同时,各标度下均值-MF-X-DMA 模型相对于传统投资组合模型贝塔系数更小,但均大于2。均值-MF-X-DMA 模型能有效削弱市场波动对投资组合造成的影响,但由于能源行业的特殊属性,系统性风险仍然偏高。

(4)基于夏普比率、詹森指数和特雷诺指数,综合衡量投资组合的收益和风险。结果显示,标普500能源指数的夏普比率小于所有传统投资组合模型,詹森指数和特雷诺指数小于除等权重模型外的所有传统投资组合模型。除标度为10之外,任一标度下均值-MF-X-DMA 模型的夏普比率、詹森指数和特雷诺指数均大于传统投资组合模型。上述指标验证,基于产业链理论的选股方式和均值-MF-XDMA 模型,能够使投资组合在单位风险下取得更高的收益,且当能源市场行情不佳时在一定程度上减小能源投资者的损失。

3.4 模型的有效边界

根据前文的比较分析,相对于传统投资组合模型,本文构建的均值-MF-X-DMA 模型在一定程度上能有效削弱风险,提高组合收益。为了进一步检验模型的有效性以及比较不同标度下模型表现的优劣,本文构建了均值-MF-X-DMA 模型的有效边界。在给定期望收益率u0的情况下,最小化多分形方差得到在此期望收益率下的最优投资组合策略,当u0取得足够多时,得到一系列的u0-组合点,这些组合点构成了模型的有效边界。根据样本股的特点,u0的范围选择0.5×10-3～1.5×10-3,标度s选择50、100、150、200、250和300。有效边界如图5所示。

由图5可知,当期望收益大于一定值后,随着期望收益u0的增大,基于任一标度下的模型对应的风险都随之增大,即高收益伴随着高风险,这符合理论结果和现实情况。同时,由图5可以发现,期望收益越高,每增加一单位收益时,其增加的风险就越大,这也符合边际收益递减的原则。由组内的对比可见,在相同的期望收益u0下,标度s越大,其所承受的风险就越大。

4 结论

受到气候、经济、政治等多重因素的影响,能源投资存在高度不确定性风险,因此,本文将分形理论、产业链理论与传统投资组合理论结合,为构建更有效的投资组合提供了新的思路。基于产业链理论选取能源样本股,结合经典均值-方差模型和MF-XDMA 方法构建投资组合模型,并与标普500 能源指数和传统投资组合模型进行比较,所得结论如下:

(1)能源样本股收益率序列均具有分形特征,存在标度不变性。采用R/S分析法,计算发现,各组样本股收益率的Hurst指数均不等于0.5,说明收益率之间存在非线性特征。因此,在构建投资组合模型时,分形市场理论比有效市场理论更为适用。

(2)基于标普500能源指数,对于按市值加权法构建的投资组合进行样本外检验。结果表明,根据产业链理论选取能源投资种类,不仅能有效分散能源价格高度波动造成的市场风险,构建稳定性更好的投资组合,而且能够深度挖掘行业价值,提高投资组合的收益率。

(3)对均值-MF-X-DMA 模型和传统投资组合模型进行样本外检验,并单独比较收益和风险水平,其中风险水平包括系统性风险和整体风险。结果表明,相对传统投资组合模型,除标度为10之外,其余标度下的均值-MF-X-DMA 模型均能取得更高的收益,并能有效削弱系统性风险的影响。当考虑投资组合的整体风险时,均值-MF-X-DMA 模型的表现则不如对照组模型。

(4)由于综合评估收益和风险更为合理,本文采用夏普比率、詹森指数和特雷诺指数进一步检验。结果表明,除了标度为10之外,任一标度下的均值-MF-X-DMA 模型均能取得比对照组模型更高的夏普比率、詹森指数和特雷诺指数,意味着该投资组合在单风险下能取得更高的收益。

随着中国金融市场双向开放程度的加深,即便国内能源市场受到政策管制,自身稳定性相对较好,国际能源价格冲击对于中国能源产业链仍然具有传导效应,且研究表明,中国金融市场自身及其与国际金融市场的相关性关系均具有多重分形特征,上述结论在国内能源市场同样适用[17,45-46]。因此,提出下述建议,便于优化国内能源产业结构以及调整海外能源资产配置,从而提升对海内外能源资产的风险管理水平,保障能源领域的金融安全。

针对能源产业结构的布局,考虑到能源产业间极强的关联性,应适当延伸链条长度,实现对产业链的纵向整合。一方面,应推动能源领域的前向投资,规避能源供应不稳定而可能造成的风险;另一方面,从供给端出发,提升对中下游环节的投资比重,指导产业链下游企业的用能方向,从而发挥提升效应。以核心行业为龙头,带动能源产业发展,保障中国能源安全和战略需求。

针对能源市场投资的配置,应考虑资本市场具备“尖峰厚尾”的多重分形特征,以分形市场理论为指导,进行全产业链布局。一方面,应合理运用分形市场理论,指导投资组合的构建,并充分发挥MFX-DMA 方法计算简便且精确度高的优势,构建在单位风险下回报水平更高的投资组合;另一方面,应进行产业链投资,合理分配资金在各个环节的权重,并在各个环节选取具有行业代表性、强盈利性及体量相近性的公司,强化对上下游环节间相对波动风险的抵消效应。