基于模拟仿真的石化油气输送系统数字孪生体技术

周 波

(中国石油工程建设有限公司 西南分公司，四川 成都 610041)

天然气能否准确计量直接影响着开发、运行、配给及用户等各方的经济利益，而管路结构的安全性是影响天然气流量计量准确性的主要因素之一。天然气管道事故常处于突发情况，需要建立能即使发现天然气输送管道的应急响应技术。

数字孪生是通过物理模型、传感器更新、运行历史等数据，包括多学科、多物理量和时间尺度及多概率的实时仿真过程，在虚拟空间中进行映射，创造一个能表达其相对应的实体设备全部周期过程的数字模型。数字孪生体的工程意义是在实际运行系统之外，构建一个与实际运行系统运行环境基本一致的虚拟化系统，且使虚拟化系统的运行时间前推一定周期，从而判断实际运行系统在未来短周期内可能发生的故障，并作出提前预警。

受制于工程逻辑学的局限性，实际搭建液化天然气((Liquefied Natural Gas，简称LNG)输送管道数字孪生体时，存在海量的隐藏传导机制和不完备数据，所以，只能通过机器学习系统搭建仿真系统，而无法实现完全一致且无需后续干预的数字孪生体。建筑信息模型(Building Information Modeling，简称BIM)系统中内置的数字孪生体的时间前推能力难以满足实际运行需求。

该研究设计了一套相对完善的基于机器学习算法的数字孪生体仿真运行算法，并对其进行了验证。

1 天然气管道电子仪表系统及数字孪生体的搭建

今天，大部分LNG天然气管道已经实现了压力、流量、温度等仪表的1 s周期远程实时抄表工作且形成了物联网大数据体系。随着量子力学发展，使用高精度三轴激光陀螺仪捕捉管道的震动，可以有效反映出管道内的气液混合情况、涡流湍流情况等。数字孪生体建设中，这些仪表采集的物联网大数据称为其主要数据来源。

该研究设计的数字孪生体，对各探头数据在BIM系统中构建数据LOD(Levels of Detail，简称LOD)技术图，且在授时系统驱动下形成图时序序列，进而使用模糊神经网络对所有图序列分别执行卷积压缩，使每个图序列形成1个双精度浮点型特征变量，再将这些特征变量输入到多列神经网络中，重新组建各个压力表、流量表、温度表在前推时间点的曲线估计前推结果数据。该数字孪生体构建策略如图1所示：

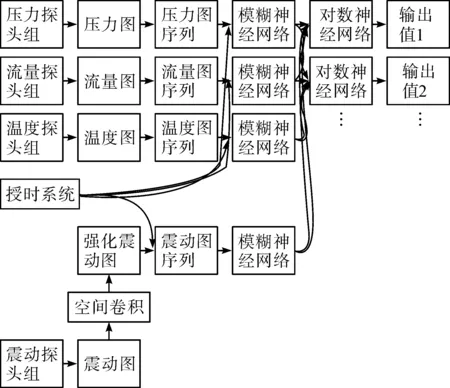
图1 图论统计支持下的多列神经网络数字孪生体系统算法逻辑

图1中，使用了图论统计法、空间卷积法、时序图序列同构化方法等数据前置治理算法，模糊神经网络、对数神经网络等机器学习算法，多列神经网络数据重构法等数据解模糊算法等，形成数字孪生体中前推一定时间周期的数据曲线估计前推模型。相关算法将在后续章节中展开论述。

2 数据融合与数字模拟仿真大数据技术体系

2.1 数据的前置治理算法

图论统计学方法

使用LOD法将仪表数据定义到BIM的三维模型中，形成数据投影。数据表达为{,,,,,,,}，其中，{}为仪表序列号，{,,}为仪表测量点的BIM三维空间坐标，{,}为仪表管道逻辑关系前后连接点，{}为仪表读数；{}为仪表读数时间戳；将相同{,,,,,}标识的序列在时间轴{}上展开，形成图序列原始统计结果；

四维时空空间卷积方法

四维时空空间卷积方法是将上述{,,,,,,,}序列，以{,,,}四个坐标维度作为卷积维度，对{}值执行空间卷积，强化特征数据，其基函数如公式(1)：

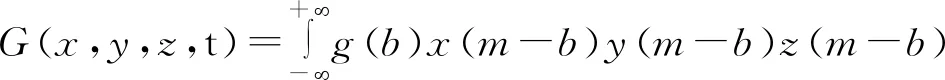
(1)

式中：(,,,)为卷积后输出结果；()为卷积核，为一个小规模四维阵列数据，不同的卷积核赋值方式会实现不同的卷积效果，如边缘强化、离群捕捉、峰值强化等；(-)(-)(-)(-)为被卷积序列分量函数；

2.2 基于机器学习的数据深度挖掘算法

基于六阶多项式深度迭代回归算法的模糊神经网络

六阶多项式深度迭代回归算法的统计学本质是将大宗数据卷积到1个双精度浮点型变量内，使其在最小的信息损失量前提下使用较小规模数据代表大宗数据的数据特征。六阶多项式深度迭代回归算法的节点基函数如公式(2)：

(2)

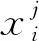
基于对数深度迭代回归算法的对数神经网络

对数深度迭代回归算法的统计学本质是利用对数曲线的非线性特征放大数据在自变量坐标轴0值附近的细节，该数字孪生体算法中，将其作为多列神经网络的节点函数，其基函数如公式(3)：

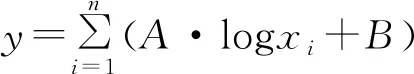
(3)

式中：、为待回归系数；其他数学符号含义同式(2)。

3 数字孪生体的仿真度验证分析

3.1 仿真验证方案

在Matlab中加载Simulink控件构建仿真环境，数据训练中，采用某单位LNG天然气输送管道中压力、流量、温度、震动加速度仪表数据作为原始数据作为原始数据，使用中间数据作为输入数据，对应的前推数据作为输出数据执行数据训练，后续类似数据组织方式组织收敛效果验证。每个特定分列的算法模块内部逻辑结构相同，根据不同的大数据训练需求对其分别训练，使其向特定的应用方向数据收敛。

验证试验中，使用仿真数据与原始数据之间的决定系数、标准偏差率和平均离群率作为验证方法。其中：

决定系数()的算法如式(4)：

(4)

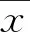
标准偏差率的算法如式(5)：

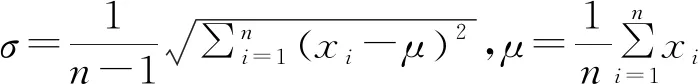
(5)

式中：为输入序列的标准偏差率；为输入序列中的第个输入项；为输入序列的算数平均值；为统计样本数量。

平均离群率的算法如式(6)：

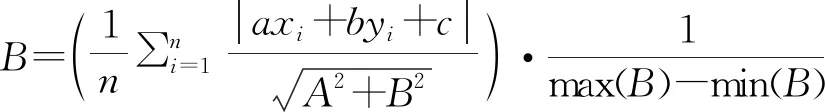
(6)

式中：为标准离群率；、、为离群率线性回归预测直线的系数;(,)为第个散点的二维空间坐标；max()；min()为离群率估计的最大值和最小值。

对数据孪生体前推时间周期曲线估计预测数据的算法效能验证方法使用验证敏感度的方式进行计算，敏感度计算方法为为数据预测值与数据实测值之差与数据实测值的比值均值，其算法如式(7)：

(7)

式中：为统计数据节点的数量；为第个数据实测值；为第个数据预测值。

3.2 流量分布数据耦合度

对天然气流量分布数据流在定时域窗口进行值域区间的数据频率分布统计和频域区间的数据分散度运算，可以建立动态的流量分布耦合数据，比较分析流量分布数据耦合度的统计如表1所示。

表1 流量分布数据耦合度统计表

表1中，决定系数一般指可决系数，表示一个随机变量与多个随机变量关系的数字特征；标准偏差率时一种度量数据分布的分散程度标准，用以衡量实际值与理论值或者估计值的偏差程度；平均离群率是多点数据集中偏离大部分数据的一种算法。

3.3 压力分布数据耦合度

天然气输送管道的渗透率和孔隙度等相关参数会随着输送压力的变换而发生动态变化,同时该变化又会影响到压力的分布状况，针对压力分布数据耦合度如表2所示。

表2 压力分布数据耦合度统计表

由表2可知，数字孪生体算法仿真在压力分布数据耦合度统计中的决定系数验证结果略高于BIM自带的结果，在标准偏差率和平均离群率的验证结果却明显低于BIM自带的数据结果。

3.4 数据前推估计敏感度

对数字孪生体算法仿真和BIM自带数据系统依据上述的系统数据耦合度验证结果数据曲线，进行系统的数据前推估计敏感度统计，如表3所示。

表3 数据前推估计敏感度统计表

由表3可知，显示数字孪生体算法仿真在5 s和曲线估计前推数据结果略高于BIM自带的结果，在15、30、60 s时的估计前推数据均明显优于BIM自带的敏感度结果，且比较结果为<10000，<005，说明具有明显统计学意义。

4 结语

通过在MATLAB中加载Simulink控件构建仿真环境，对流量分布和压力分布的数据耦合度，以及数据前推估计敏感度进行了测试，结果证明了数字孪生体算法仿真能够有效的对异常数据预警和主动推送，能够提高系统应用的安全性，具有很好的应用价值。