关联规则算法在卫星定位精度考核中的比较分析

钱昭勇，曹裕华，史增凯，张 雷

(1.航天工程大学，北京 102206；2.国防大学联合勤务学院，北京 100858；3.西安卫星测控中心，陕西 西安 710043)

1 引 言

卫星导航系统定位的精确性是其在役考核过程中的关键问题。影响定位精确性的多维度因素可以理解为多指标评价问题，各指标间并不一定完全独立，分析指标间相互影响的关联规则有助于更好地掌握和改进定位方式和策略，规避相关风险和误区。马宁等[1]认为装备体系是一个复杂系统，系统中各元素在执行任务的过程具有一定的关联和协同关系。传统的效能评估体系框架大多采用同一等级各元素相互独立的树形结构，从而忽略指标间的各种相关关系，指出可以基于大量仿真数据进行分析，挖掘各指标间的关联关系，使得评估结果可信度更高[2,3]。

研究与定位精度相关联的指标和规则，首先要明确所选择指标的范围，因为影响定位精度的因素很多，既有定性指标，又有定量指标，既有卫星和接收机等系统因素，又有目标运动状态、采样率等人为因素，选择合适的指标范围(例如，可选择全部指标集或部分相关性更高的指标集)将直接影响考核评估的结果。其次，分析指标间关联关系的方法有很多，其中，最经典的关联算法是Apriori和FP-Growth，在分析航天器异常[4，5]、评价指标信息挖掘和指标约简[6]、业务对口推荐和广告推送等方面都有广泛应用价值[7]。本文从关联规则数量和实效两个维度对比这两种算法在不同数据范围的挖掘结果，探索关联规则算法在卫星定位精度分析中的适用性，以期得到有意义的结论。

2 相关理论

2.1 Xgboost算法

Xgboost的全称是eXtreme Gradient Boosting，主要通过将多个弱分类器集成转化为一个强分类器，从而达到更精准的分类或者预测效果，同时其可以给出因子的重要性排序[8]。通过使损失函数在迭代过程中沿梯度方向下降，从而提升算法的稳定性。在此基础上对损失函数进行二阶泰勒展开，并在损失函数之外对正则项求得最优解。具体的重要性指标评价包括两步：第一，求出每个特征的得分score；第二，求出各特征得分占比score/sum(score)。

2.2 Apriori算法

Apriori模型是由Agrawal等[9]在1994年提出的关联规则挖掘方法，使用支持度作为判断频繁项集的标准，其目标是找到最大的K项频繁集。Apriori算法具体步骤如表1所示。

表1 Apriori算法流程

2.3 FP-Growth算法

FP-Growth算法采用分治策略[10]，与Apriori的最大区别在于其不产生候选集，只需两次遍历数据库，算法具体步骤见表2。

表2 FP-Growth算法流程

3 分析流程与指标筛选

3.1 基于指标筛选的关联分析流程

关联分析可识别指标间的关联性和相关性，即可以确定与定位精度关联度更高的指标。当指标较多时，算法计算时长和复杂度都会随着维度的增加而增加。为此，不仅可以在所有指标上进行关联规则挖掘，也可以先缩小搜索范围，使用Xgboost算法确定各指标对定位精度影响度的高低，把搜索范围改为与定位精度相关度更高的指标，从而提高算法效率。总体而言，相关流程如图1所示。

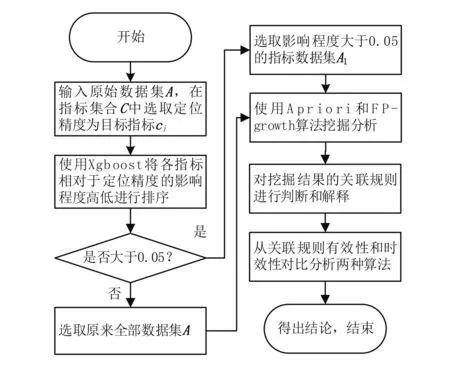
图1 卫星导航系统定位精度考核关联分析

3.2 相关指标筛选

采用某中心的仿真数据集，包含13个变量，共30162个样本。表3详细描述了变量名称、标签和含义。

表3 数据变量和含义

由于影响导航系统定位精度的指标参数数量巨大，如果分析挖掘所有指标(全域)属性的关联关系，将导致规则数量太过繁杂，且运行时间难以接受。通过构建Xgboost模型得到对定位精度指标影响程度高的指标排序，如图2所示，对定位精度指标影响程度高的指标依次为：DOP值A10，导航系统类型A1，轨道类型A11，观测值类型A9，采样率A4，载噪比A5，目标运动状态A3，误码率A6，接收机类型A8，传输时延A12，信号频点A7，信号捕获概率A2。设置指标重要性大于0.05为高影响程度，其指标参数集即为精简域，包括DOP值、导航系统类型、轨道类型、观测值类型、采样率、载噪比。

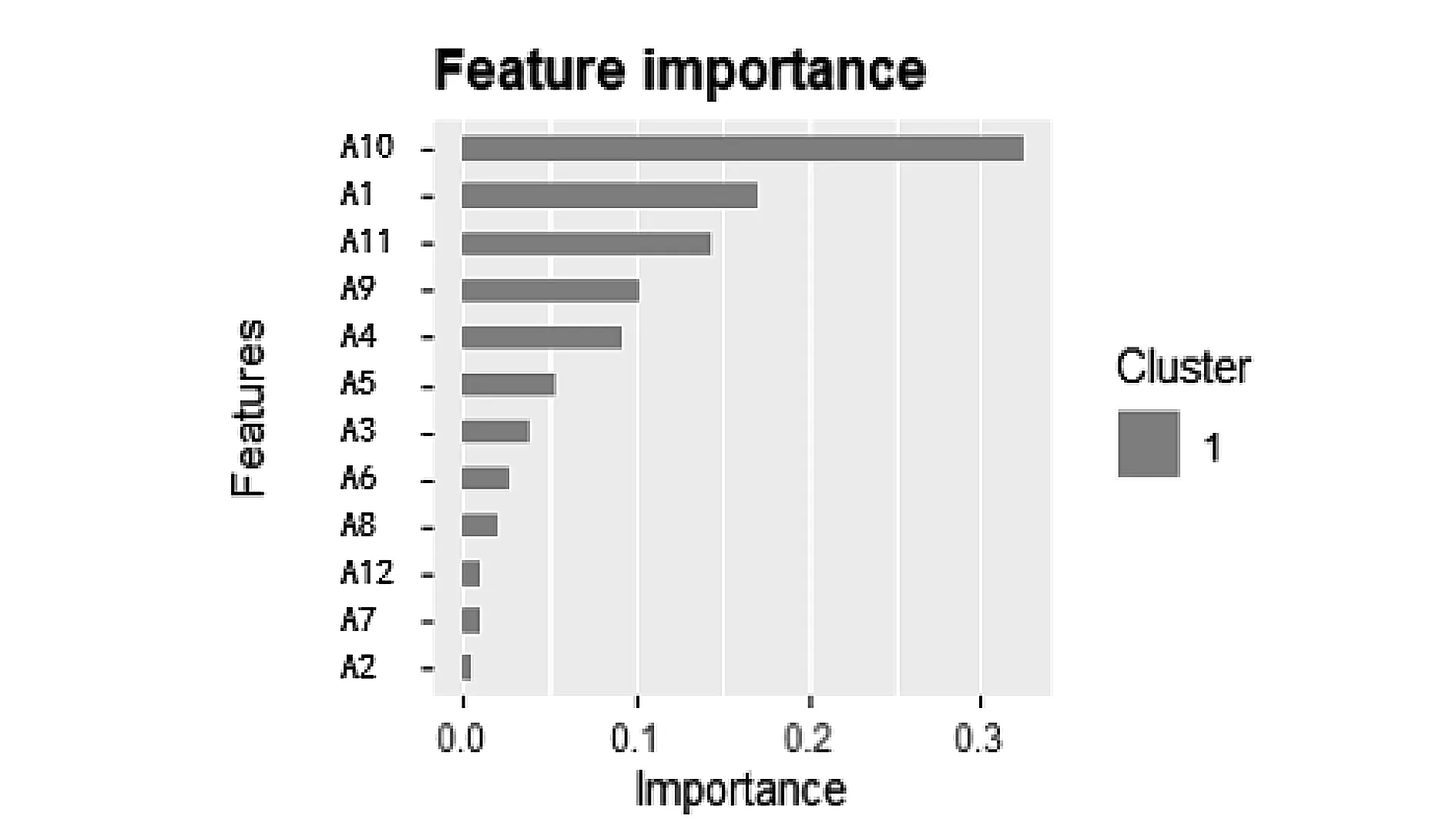
图2 对定位精度影响的重要性排序

4 实验分析

4.1 评价指标

设置有效规则为最小支持度0.05，最小置信度0.8，选择定位精度作为定位精度，而关联指标搜索范围为全域和精简域。本节主要选用有效性作为算法对比的指标，包括两个方面含义：一是算法最终产生的关联规则中只有用户感兴趣的事务项即目标事项，才对用户有意义，这时的关联规则才是有效的；二是挖掘出的规则置信度和支持度是有要求的，低置信度和支持度的规则不能称为有效关联规则。为检测这两个方面，定义3个有效性公式对算法进行评估，具体有效性公式如下：

E1=N1/N
E2=N2/N
E3=N2/N1

(1)

(2)

(3)

式中，N1是符合置信度和支持度要求的规则数量，N2是指符合置信度和支持度要求且与定位精确度相关的规则数量，N指的是整体挖掘规则的数量。

4.2 Apriori与FP-Growth全域关联挖掘

基于经典Apriori算法，实验共提取了223378条规则(如图3所示)，用时42.76s。其中，符合有效条件的关联规则31495条(如图4所示)，按照lift排序在表4中展示前5条内容，均属于4个或5个因素得出结论的关联规则。

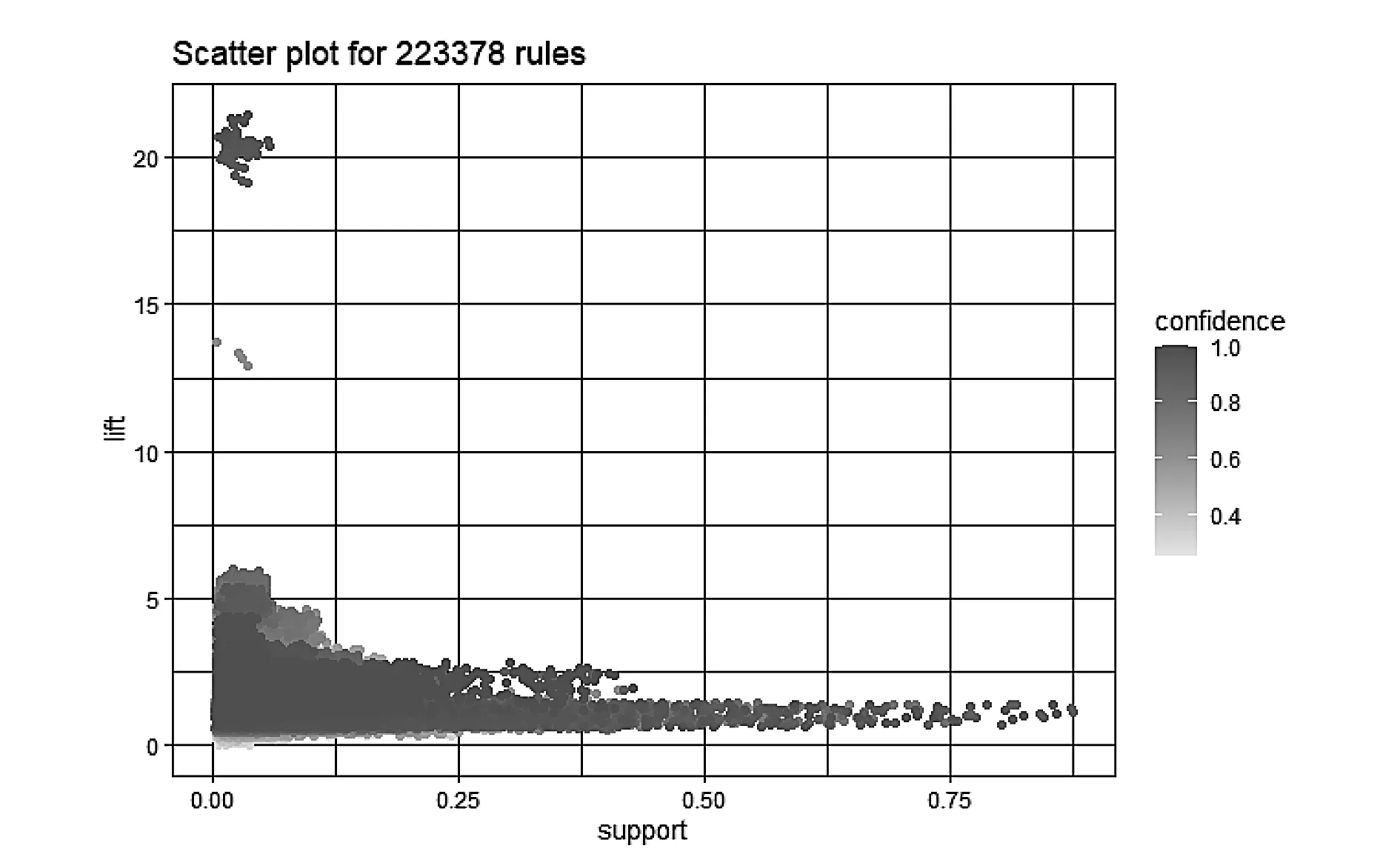
图3 Apriori全域提取的关联规则N

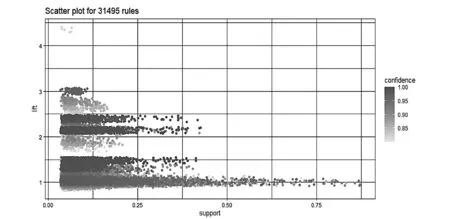
图4 Apriori全域提取的关联规则N1

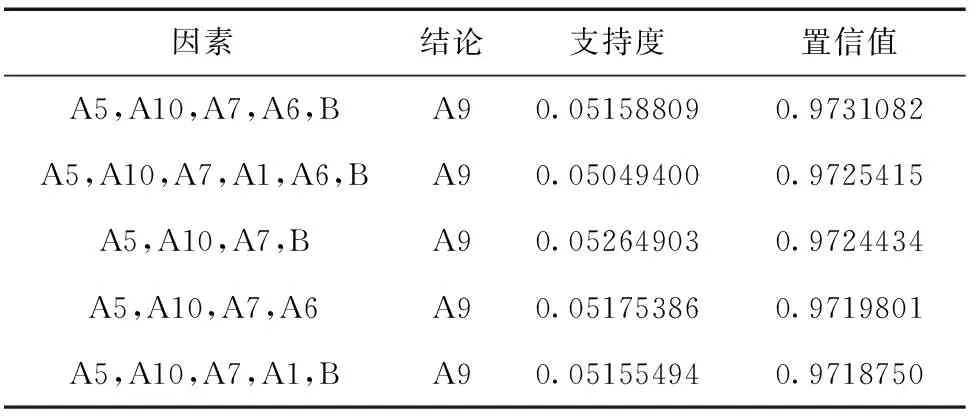
表4 Apriori全域提取的关联规则N1(前5条)

表中各变量具体取值：载噪比A5=低，误码率A6=高，信号频点A7=低，DOP值A10=高，定位精确度B=低，观测值类型A9=多普勒观测值。其中，以定位精确度作为结论的规则共2429条(如图5所示)，同样地，按照lift排序在表5中展示前5条内容。

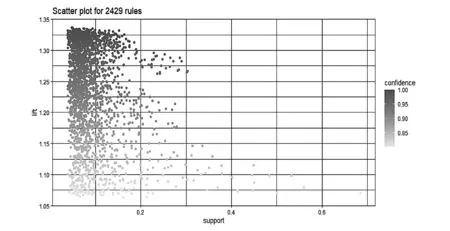
图5 Apriori全域提取的关联规则N2

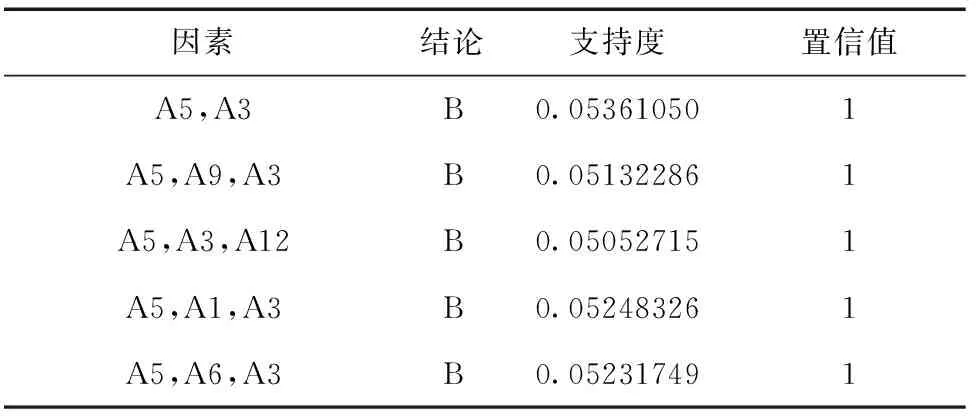
表5 Apriori全域提取的关联规则N2(前5条)

表中各变量具体取值为：导航系统类型A1=GPS/Galileo/GLONASS/北斗某单一类型，目标运动状态A3=动态，载噪比A5=低，误码率A6=高，观测值类型A9=多普勒观测值，定位精确度B=低。

在相同实验背景下，使用FP-Growth算法共提取14263条规则(如图6所示)，用时3.21s，符合有效条件的关联规则为1250条(如图7所示)，按照lift排序在表6中展示前5条内容，发现这些规则都是以定位精度为结论。

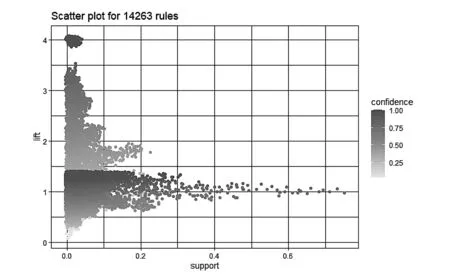
图6 FP-Growth全域提取的关联规则

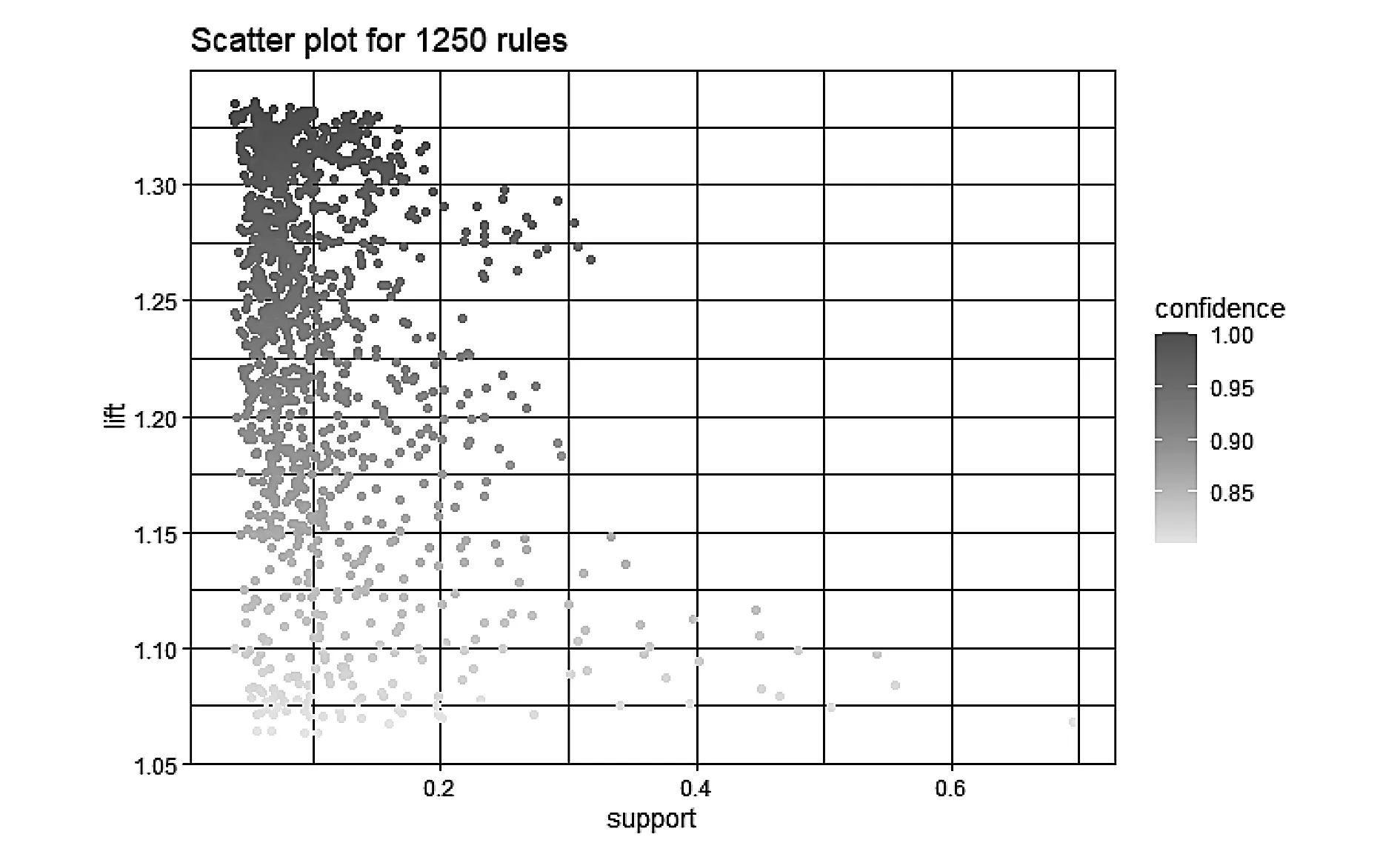
图7 FP-Growth全域提取的关联规则N1=N2

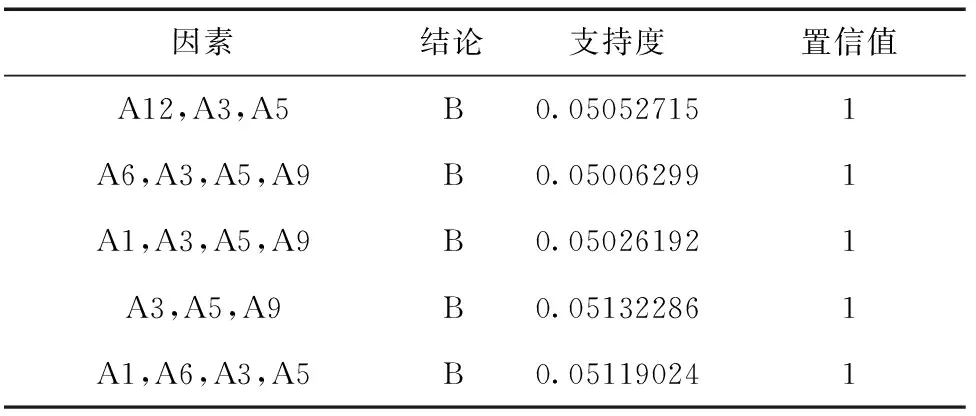
表6 FP-Growth全域提取的关联规则N1=N2(前5条)

表中各变量具体取值：导航系统类型A1=GPS/Galileo/GLONASS/北斗某单一类型，目标运动状态A3=动态，载噪比A5=低，误码率A6=高，观测值类型A9=多普勒观测值，传输时延A12=高，定位精确度B=低。

由式(1)-式(3)，Apriori挖掘有效性计算得：

E1=31495/223378=14.1%

(4)

E2=2429/223378=1.1%

(5)

E3=2429/31495=7.7%

(6)

同理，FP-Growth挖掘有效性计算得：

E1=1250/14263=8.8%

(7)

E2=1250/14263=8.8%

(8)

E3=1250/1250=100%

(9)

从上面的分析可知，设置同样的数据集，同样的条件参数，Apriori算法挖掘关联规则有效性比FP-Growth算法挖掘关联规则有效性指标E2和E3低，尤其是E3，只有评价指标E1略高。

4.3 Apriori与FP-Growth精简域关联挖掘

将搜索范围改为上述6个影响程度高的指标集数据(精简域)进行实验。Apriori算法共提取2621条规则(见图8)，用时1.75s，符合有效规则条件的关联规则为310条(见图9)，按照lift排序在表7中展示前5条内容。表中所示的规则属于2、3和4个因素结论的关联规则。挑选与定位精度作为结论的有效规则共66条(见图11)，按照lift排序在表8中展示前5条内容。通过表8中的规则，同样可以得到类似结论，当导航系统类型A1=GPS/Galileo/GLONASS/北斗组合类型，载噪比A5=高，DOP值A10=低，观测值类型A9=载波相位，可以得出定位精度B=高的关联规则结论。

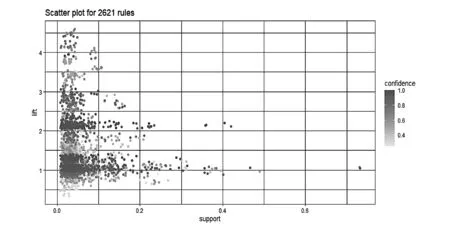
图8 Apriori精简域提取的关联规则N

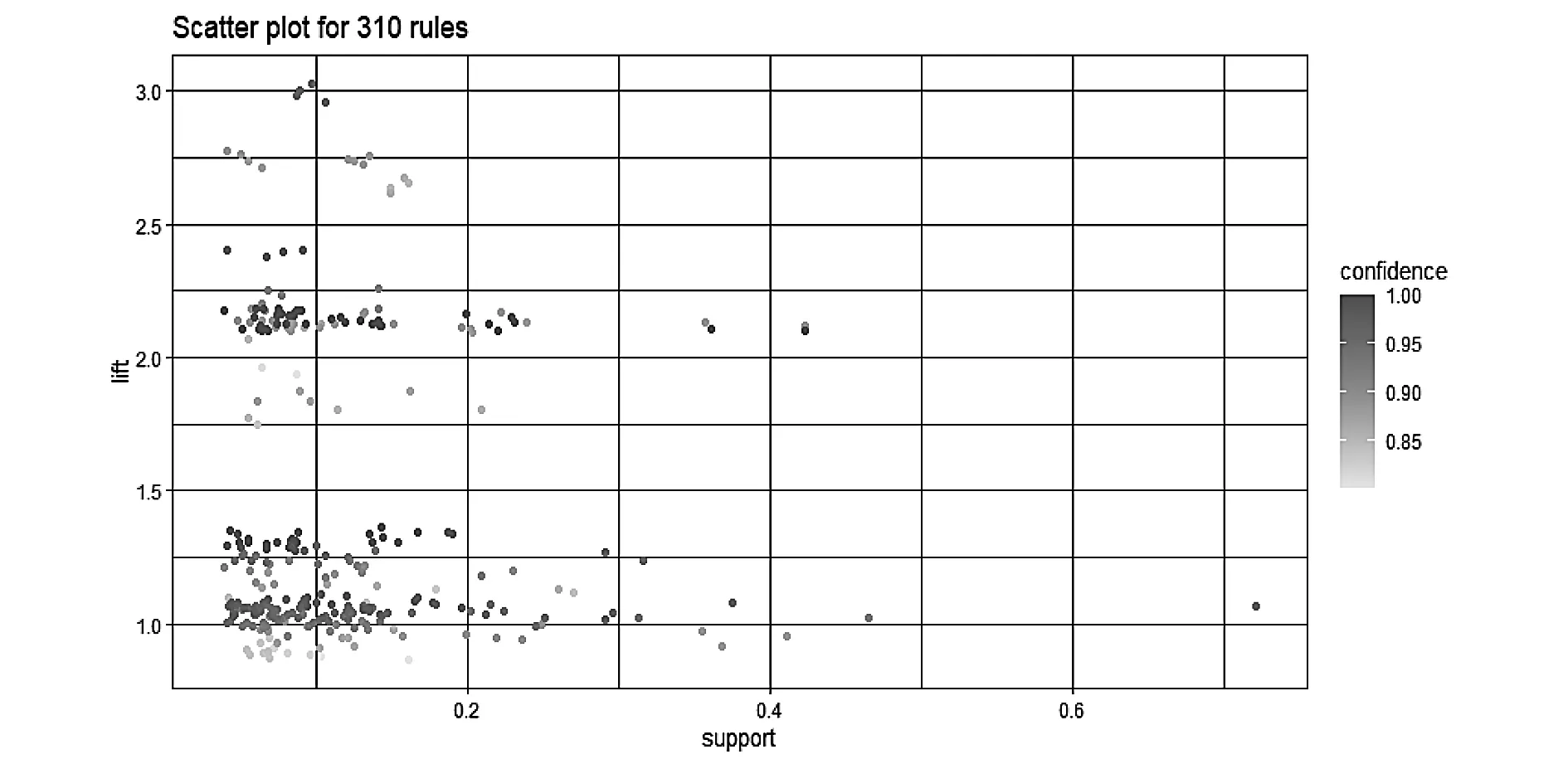
图9 Apriori精简域提取的关联规则N1

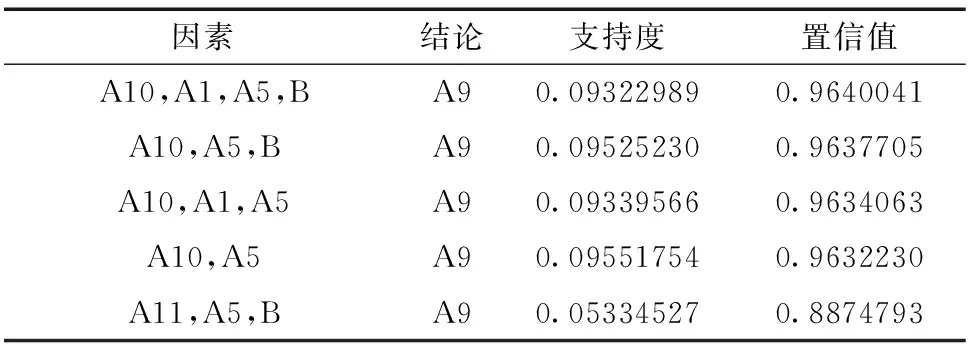
表7 Apriori精简域提取的关联规则N1(前5条)

表中各变量具体的水平值：导航系统类型A1=GPS/Galileo/GLONASS/北斗某单一类型，载噪比A5=高，DOP值A10=高，轨道类型A11=GEO/IGSO/MEO组合类型，定位精确度B=低，观测值类型A9=多普勒观测值。

在相同实验背景下，使用FP-Growth算法共提取1077条规则(如图10所示)，用时0.22s，符合有效规则条件的关联规则为66条(如图11所示)，按照lift排序在表8中展示前5条内容。这些规则同样都是以定位精度为结论。

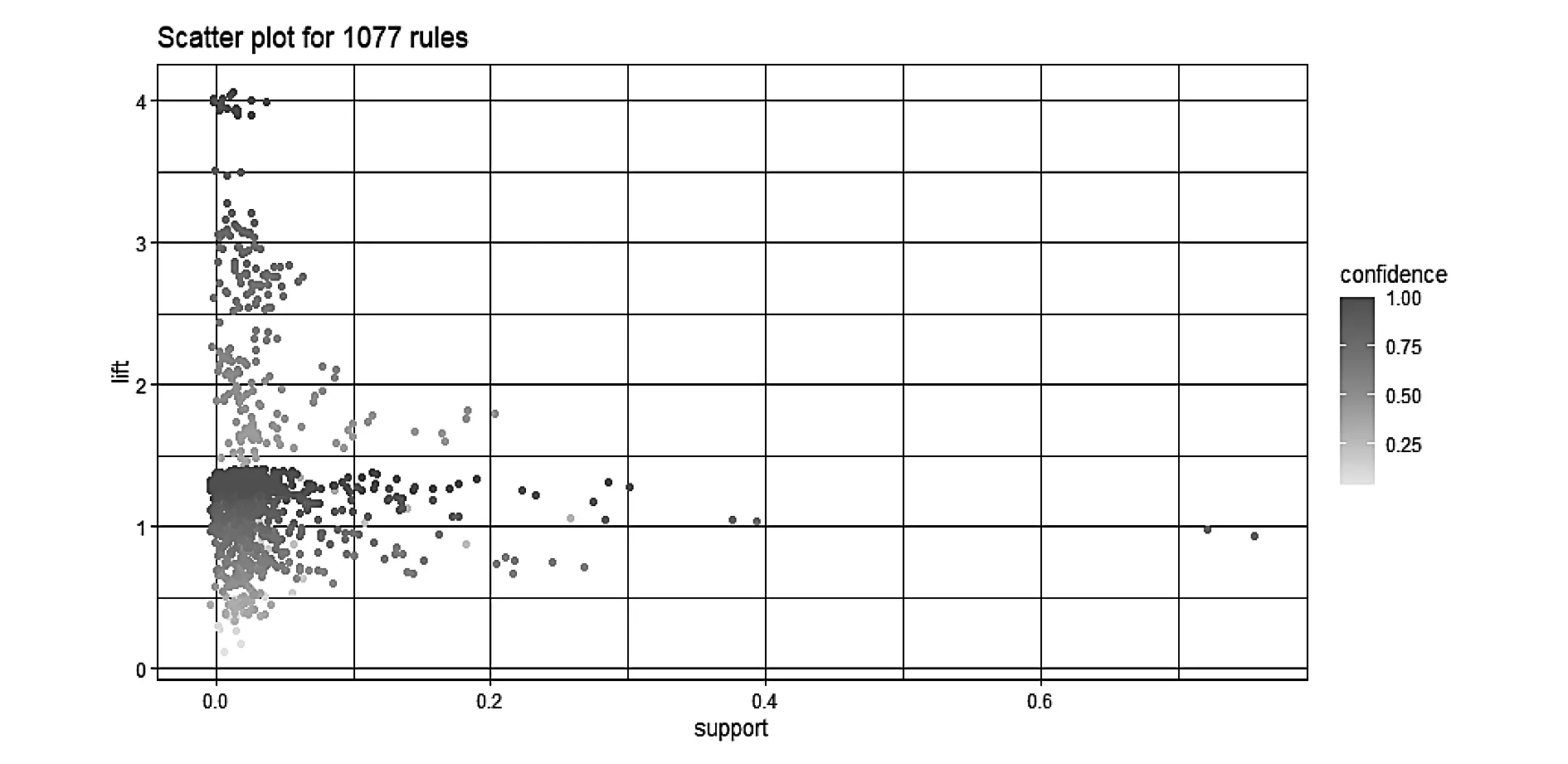
图10 FP-Growth精简域提取的关联规则N

图11 Apriori与FP-Growth精简域提取的关联规则N2

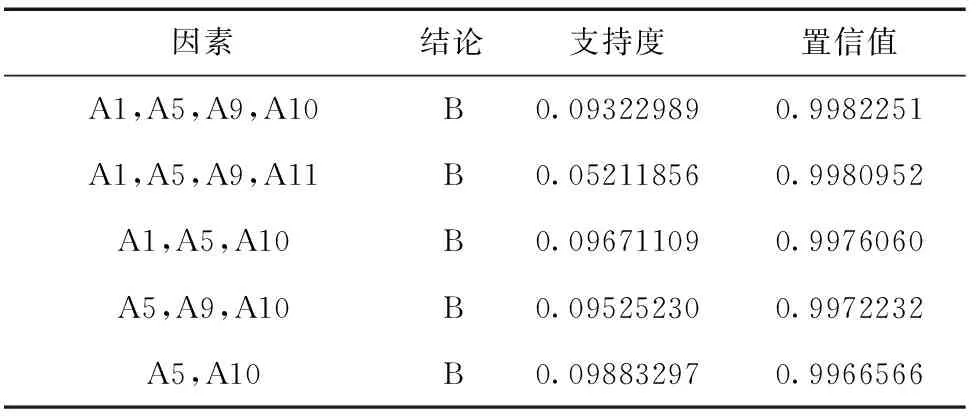
表8 FP-Growth精简域提取的规则(部分)

表中各变量具体的水平值：导航系统类型A1=GPS/Galileo/GLONASS/北斗某单一类型，载噪比A5=高，观测值类型A9=载波相位，DOP值A10=低，轨道类型A11=GEO/IGSO/MEO组合类型，得出结论：定位精确度B=高。

Apriori挖掘有效性，由式(1)-式(3)计算得：

E1=310/2621=11.8%

(10)

E2=66/2621=2.5%

(11)

E3=66/310=21.3%

(12)

FP-Growth挖掘有效性，由式(1)-式(3)计算得：

E1=66/1077=6.1%

(13)

E2=66/1077=6.1%

(14)

E3=66/66=100%

(15)

综合4.2、4.3部分的讨论，并将指标对比，无论是在全指标情况下还是在与定位精度影响程度高的指标范围内，Apriori算法挖掘关联规则有效性指标E2和E3比FP-Growth算法挖掘关联规则的有效性指标都低一些，而有效性指标E1略高一些。这里需要格外关注有效性指标E3，FP-Growth算法得到的符合置信度和支持度的指标都是以定位精度为结论的规则，提取有效规则的效率大大提升。从FP-Growth算法与Apriori算法在不同指标范围下生成关联规则数量对比可以得出，FP-Growth算法相比Apriori算法生成的关联规则要少。在全域范围时，FP-Growth相比Apriori算法生成的符合置信度和支持度要求且以定位精度为结论的规则占整体规则的比例增加7.7%，符合置信度和支持度要求且以定位精度为结论的规则占有效规则的比例增加92.3%。在精简域范围时，FP-Growth相比Apriori算法生成的符合置信度和支持度要求且以定位精度为结论的规则占整体规则的比例增加3.6%，符合置信度和支持度要求且以定位精度为结论的规则占有效规则的比例增加78.7%。

5 结 论

指标的关联性作为多维度指标分析的关键点，是进行数据多维度分析的切入点。将与定位精度影响度高的指标作为关联指标的搜索范围，便于得到更有实际指导意义的结果。在此搜索范围应用关联算法，可以针对定位精度不同的水平得到不同的强关联指标。无论是在全指标情况下还是在对定位精度影响程度较高的指标范围内，Apriori算法比FP-Growth算法挖掘的符合置信度和支持度要求的关联规则数量更多，但所需时间也更长，说明Apriori算法可以充分而全面地挖掘关联规则，但时效性相对较弱。在关联规则结论指标为定位精度后，FP-Growth算法挖掘的有效性和时效性都更好。当然，挖掘规则的正确性和实用性应在下一步予以充分考虑。为此，应该结合具体的导航应用场景和任务分析需求，选择不同的挖掘方法，为解决考虑关联的多指标评价问题提供参考思路。