基于自然梯度提升的静态电压稳定裕度预测及其影响因素分析

2022-09-27王强，陈浩，刘炼

电力系统及其自动化学报 2022年9期

王强，陈浩，刘炼

（三峡大学电气与新能源学院，宜昌 443000）

随着我国经济的发展，对于电力负荷的需求日益增长，使得电力系统越来越接近其稳定运行的极限[1]。然而，电力系统稳定裕度的降低导致发生全网性事故的概率大大增加，且频繁发生的大停电事故都会引起巨大的社会经济损失[2]。因此，进行静态电压稳定裕度VSM（voltage stability margin）在线监测，对于电力系统的稳定运行具有重要意义，也有助于充分挖掘电力系统的运行潜力。

传统基于机理分析的VSM评估方法，例如连续潮流法[3]、奇异值分解法[4]等，通常根据当前运行点到电压崩溃点的距离，来评估当前运行点的电压稳定状况。然而，该类方法依赖于离线计算，其计算速度难以满足VSM在线监测的实际要求[5-6]。

随着新一代智能电网的建设，广域测量系统WAMS（wide area measurement system）/相量测量单元PMU（phasor measurement unit）逐渐普及，为电力数据的储存与采集提供便利[7]。因此，为有效利用PMU监测数据，研究人员逐渐将机器学习技术应用于VSM 评估中。应用机器学习方法无需建立系统数学模型，只需建立运行状态变量到系统VSM间的非线性映射关系，并根据该映射关系便能实现VSM在线预测。与机理分析相比，机器学习方法具有计算速度快、泛化能力强的优点[8-9]。在最近的研究中，例如决策树[10-11]、梯度提升决策树GBDT（gradient boosting decision tree）[12]、极限梯度提升XGBoost（extreme gradient boosting）[13]、随机森林RF（random forests）[14]、反向传播BP（back propagation）神经网络[5-6]等机器学习算法已得到初步应用。

尽管机器学习方法在电力系统VSM 评估领域中已有了一定进展，但仍然存在着以下问题：①随着现代电力系统的广域互联、大规模新能源的并网，以及大量电力电子设备的投入运行，现代电力系统的VSM评估问题更加复杂[15]，传统算法的综合性能可能无法满足VSM在线预测的实际需求，一些新型机器学习算法展现出了更加优异的性能，若将新型算法应用于VSM 预测中有望进一步提升VSM预测的精准度；②机器学习模型通常只给出预测的结果，即存在“黑箱问题”[16]，人们无法捕获到预测模型从数据中所获取到的知识，因而难以将特征输入量与模型预测联系起来。

针对上述问题，本文采用自然梯度提升NGBoost（natural gradient boosting）[17]算法来构建VSM预测模型。NGBoost 具有优良的综合性能，能够弥补传统算法在精度、鲁棒性及泛化能力上的不足，保证预测结果的可靠性。同时，引入沙普利值加性解释SHAP（Shapley additive explanations）[18]理论对NGBoost 模型进行解释，构建基于SHAP 理论的VSM预测影响因素分析架构，量化各输入特征对于模型预测的边际贡献。结合预测结果，通过全局分析角度可得到各特征的重要性程度，以及各特征对于模型预测的正负影响。通过个体分析角度可以明确单个样本中各特征对VSM 预测的具体影响过程，从而找到导致系统VSM 降低的关键因素，进而为预防措施的制定提供理论依据。

1 VSM 与离线样本集的构建

1.1 VSM

采用连续潮流法绘制系统的P-V曲线来描述节点电压与负荷有功功率间的相关性，并通过P-V曲线得到系统的电压稳定临界点，P-V曲线示意如图1所示。

图1 P-V 曲线示意Fig.1 Schematic of P-V curve

从图1 可以看出，当负荷有功功率增大时节点电压会逐渐降低，当增加到负荷有功功率极限时系统将无法提供足够的无功功率从而导致电压崩溃，此时系统则位于电压稳定的临界点。因此，电力系统当前运行点的负荷有功功率到电压稳定临界点的负荷有功功率之差可以综合反映电力系统的VSM。VSM可表示为

式中：Pmax为电压稳定临界点的负荷有功功率；P0为电力系统当前运行点的负荷有功功率。

1.2 离线样本的构建

使用PSS/E 软件进行模拟仿真，并调用Python程序进行仿真数据的自动采集。在构建样本时，应综合考虑多种影响因素，包括发电机/负荷功率的不确定性、网络拓扑结构变化等。模拟仿真的具体步骤如下。

步骤1考虑负荷功率的不确定性，将各个负荷视为一个服从概率分布的随机变量，并根据其分布函数确定负荷参数。同时，考虑实际中的发电机、线路传输容量等约束条件，利用最优潮流来确定相关变量，例如有功/无功功率分布、分接开关位置等。然后，生成初始的发电机/负荷功率分布。

步骤2发电机/负荷功率在不同的增长方式下将会产生不同的电压稳定边界，发电机/负荷功率的具体增长方式可表示为

式中：PG为发电机有功功率；PL、QL分别为负荷有功功率、无功功率；为发电机初始有功功率；、分别负荷初始有功功率、无功功率；分别为发电机有功功率、负荷有功功率和负荷无功功率的增长方向，在实际中，可在电网的优化调度及负荷预测中获取[19]；λ为负荷参数。

为获得更多的样本，将不同区域内的负荷增长率设置为不同，并保持功率因数不变。同时，增长的负荷由同一区域内的发电机按初始出力比值共同承担。

步骤3拓扑结构变化是另一个需要考虑的因素。在实际中，可信的紧急事故列表可在电力公司中获取到。根据网络拓扑结构和发电机/负荷功率增加方式，使用连续潮流法来确定电压稳定的临界点，并通过式（1）计算VSM，记录该过程中系统所有运行点的运行状态变量。

以当前运行点的状态变量为特征，并建立特征与相应VSM 间的对应关系。所选择的特征类型如表1所示。

表1 选择的特征类型Tab.1 Selected feature types

2 基于NGBoost 的VSM 预测模型

2.1 NGBoost 算法

NGBoost 是一种针对概率预测的监督学习方法，对于输入特征的预测则通过条件概率分布的形式实现。NGBoost 由基学习器（例如回归树）、概率分布（例如正态分布）、评分规则（例如最大似然估计）3个模块构成，并使用自然梯度对这些模块进行整合。

评分规则S与概率分布p和标签y相关，并记为S（p，y），为使预测结果真实分布的期望值得到最佳的分数，则评分规则S需满足

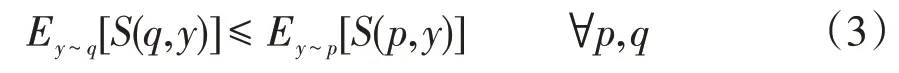
式中：Ey～q()为标签y服从q概率分布的期望函数；q为标签y的真实分布。在训练中，适当的评分规则可用于校准模型的概率分布输出，为限制概率分布的参数化，概率分布则根据预测参数θ来确定。若选用最大似然估计MLE（maximum likelihood estimation）作为评分规则S，则S可表示为

式中：pθ(y|x)为预测参数θ的条件概率密度函数；x为标签y所对应的特征向量。

评分规则S在条件概率密度函数pθ(y|x)上关于预测参数θ的梯度记为，并且梯度方向为误差下降最快的方向。对于自然梯度g，通过求解相应的优化问题[17]可表示为

式中，IS(θ)为在预测参数θ上统计流形的黎曼度量，其可由评分规则S推导出[17]。此外，自然梯度具有参数不变的性质，且更高效和稳定。

若有训练集，则NGBoost算法的具体训练过程可描述如下。

输入：训练集D、迭代次数M、学习率η、预测参数θ、评分规则S、基学习器f。

步骤1计算初始预测参数

步骤2执行M次迭代，在第m（m=1，2，…，M）次迭代中，计算自然梯度，预测参数θ(m)的每个组成部分对应一个基学习器。

步骤3以为输出，拟合f(m)。例如在拟合回归树时，通常采用样本方差作为分割准则。

步骤4通过线性搜索的方式获取比例系数

步骤5计算

输出：θ(0)和

通过上述训练，若给定测试集E，其预测参数θ则可计算为，进而产生条件概率密度为的概率预测。其中，ρ(m)为比例系数；f(m)(x)为拟合的基学习器。

2.2 VSM 预测模型的建立

构建VSM 预测模型的本质是建立特征到相应VSM间的非线性映射关系，将所获取的离线样本构造成矩阵J的形式，即

式中：b为样本数目；c为样本中的特征维数；xi,j为输入特征，i=1，2，…，b；j=1，2，…，c；yi为相应的VSM。

首先，将离线样本集中的一部分样本作为训练集，另一部分样本作为测试集；然后，将训练集输入NGBoost算法，并根据第2.1节中所描述的步骤进行迭代学习，探索输入特征与VSM间的非线性映射关系，建立NGBoost驱动的VSM预测模型；最后，在训练集上对VSM预测模型的性能进行测试。

3 基于SHAP 的VSM 预测影响因素分析

3.1 SHAP 理论

SHAP 是由Shapley 值启发的可加性解释模型。Shapley值是合作博弈论中的一个概念，常用于量化每个玩家对于游戏的贡献。将SHAP用于解释NGBoost 模型时，样本中每个特征都会分配到一个数值（即SHAP 值），并根据SHAP 值来量化每个特征对于模型预测结果的贡献。对于某个具体的样本，其第i个特征的SHAP值的计算公式为

式中：Φi为某个具体样本中第i个特征的SHAP值；N为训练集中所有特征的集合，其特征维数为c；{}i为第i个特征；Z为从特征集N中选取的特征子集，特征维数为 ||Z；fx(Z∪{i})和fx(Z)分别为在特征子集Z的基础上添加特征i和不添加特征i的情况下NGBoost模型的预测值。

3.2 VSM 预测的影响因素分析架构

将SHAP 理论用于分析VSM 预测中的关键影响因素时，可分为全局分析和个体分析两个角度。

（1）全局分析。通过对SHAP 值按照特征维度聚合计算平均绝对值，可得到影响VSM预测的关键特征，根据关键特征分布则能够大致掌握影响电压稳定的主导特征。此外，通过绘制特征输入值与该特征SHAP 值间的散点图，便可以了解到特征输入值与预测影响间的联系。

（2）个体分析。对于某个具体样本，其预测值等于基准值（即训练集中所有样本的VSM 平均值）加上该样本中所有特征的SHAP 值。因此，根据某个特征的SHAP 值便可以了解到该特征使系统的VSM降低或升高的具体数值。

综上所述，本文基于NGBoost 的VSM预测及其影响因素分析的具体框架如图2所示。

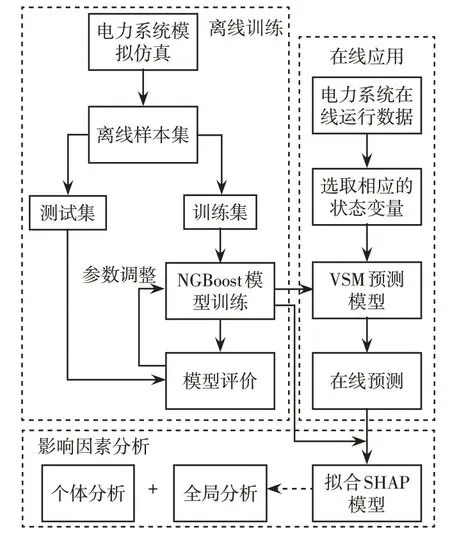
图2 VSM 预测及其影响因素分析的具体框架Fig.2 Specific framework of prediction of VSM and analysis of its influencing factors

首先，通过模拟仿真获取包含大量运行数据和VSM 的离线样本集，并将一部分样本用于训练，另一部分用于测试；然后，将训练集输入NGBoost算法进行离线训练，构建NGBoost驱动的VSM预测模型，并在测试集上对模型性能进行评价；最后，将训练好的NGBoost 模型用于拟合SHAP 模型，对训练集进行全局分析，对具体的单个样本进行个体分析。

在NGBoost 模型的预测精度满足要求后，便可以将其应用于VSM 的在线监测中。首先，使用PMU 进行电力系统在线运行数据的实时采集；然后，在调度中心接收到系统在线运行数据时，选取出相应的状态变量，输入已训练好的NGBoost 模型进行VSM值的在线预测；结合预测结果并通过拟合好的SHAP模型得出影响VSM预测的关键因素。

4 算例分析

在新英格兰39 节点系统上进行性能测试，以验证所提出的VSM 预测方法的有效性。新英格兰39 节点系统拓扑如图3 所示，该系统由39 个节点、10 台发电机和46 条输电线路组成。采用第1.2 节中所描述的方法进行模拟仿真，完成仿真步骤后共收集到2 130个样本用于后续的测试。所有测试均在一台装有Intel Core i5处理器和8 GB内存的计算机上进行。

图3 新英格兰39 节点系统拓扑Fig.3 Topology of New England 39-bus system

4.1 性能评价指标

本文采用均方根误差RMSE（root mean squared error）和残差平方误差R-squared（residual squared error）[20]作为预测模型的性能评价指标。对于RMSE指标，其计算公式为

式中：d为测试集的样本个数；yi为VSM的实际值；为VSM的预测值。RMSE值越小，则预测模型的拟合效果越好。对于R-squared指标，其计算公式为

式中，为测试集中所有样本的VSM 平均值。Rsquared值介于0到1之间，越接近1，则模型的预测效果越好。

4.2 NGBoost 模型的预测效果分析

将全部样本的80%用于训练，另外20%用于测试，并将回归树作为NGBoost 算法的基学习器，其他参数均设置为默认参数。依据式（8）和式（9），计算出测试集的RMSE 和R-squared 分别为0.007 1、0.987 6。NGBoost 模型的拟合效果如图4 所示，其中每个点代表1个样本，越靠近斜线则说明拟合效果越好。从图4可看出，所有点与斜线基本重合。

图4 NGBoost 模型的拟合效果Fig.4 Fitting effect of NGBoost model

此外，NGBoost 模型对整个测试集（包含426个样本）的计算时间为1.26 s，对单个样本的计算时间为2.96 ms。可见，NGBoost 算法的计算速度能够满足在线预测时数据处理速度的要求，即PMU 数据的处理时间应小于33 ms[19]。

4.3 不同算法间的对比分析

为进一步验证NGBoost 算法的优异性能，选取工程领域中常用的3 种算法LightGBM[21]、RF、深度残差网络DRN（deep residual network）[22]进行对比分析。对于上述3 种算法采用默认参数，并从以下3个方面对不同算法进行综合比较。

（1）在原始样本集基础上，训练和测试都使用相同的数据集以比较不同算法的预测精度，具体的测试结果如表2所示。

表2 不同算法的预测精度Tab.2 Prediction accuracy of different algorithms

（2）考虑到在实际中可能存在着数据噪声的情况，因而在样本集中添加不同信噪比的高斯白噪声以分析不同算法的鲁棒性，具体的测试结果如图5所示。

图5 不同噪声水平下各算法的预测精度Fig.5 Prediction accuracy of different algorithms at different noise levels

（3）改变原始网络的拓扑结构生成新的样本用于测试，以分析不同算法的泛化能力。图6给出了两种N-1故障下不同算法的R-squared。

图6 N-1 故障下不同算法的预测精度Fig.6 Prediction accuracy of different algorithms under N-1 failure

通过上述测试结果可看出，在原始样本集中NGBoost 的精度远高于另外3 种算法。其中，相较于LightGBM、RF 和DRN，NGBoost 的RMSE 分别降低了0.005 2、0.005 0、0.002 9，且R-squared 分别提升了0.016 1、0.015 1、0.008 4。此外，NGBoost 是基于多棵回归树的集成模型，并以条件概率分布的形式作为输出，因而增加了输出的多样性。因此，NGBoost的鲁棒性和泛化能力也优于另外3种算法，在噪声水平为15 dB及N-1故障下，NGBoost的预测精度几乎未受到影响。

LightGBM 和RF 也均为回归树的集成学习模型，由于采用了默认参数，因而在原始样本集中LightGBM 的预测精度略低于RF。同时，LightGBM和RF也都存在因回归树过深从而导致模型泛化能力降低的情况，但LightGBM 在leaf-wise 上增加了1个最大深度限制[21]，因而泛化能力略好于RF。此外，这两种算法对于噪声点也同样敏感，在噪声水平达到15 dB 的情况下，LightGBM 和RF 的Rsquared分别降低了0.007 2和0.008 9。

DRN属于深度学习的范畴，通过对时空位置建模，DRN能够很好地挖掘图像、语音、文本等高维数据，但回归树模型在处理表格数据时更具优势。在原始样本集中，DRN 的预测精度仅次于NGBoost，但是DRN 对样本质量的依耐性较强，因而在噪声水平为15 dB的情况下R-squared降低了0.007 4。同时，在两种N-1故障下DRN的R-squared为0.971 1，下降了0.008 1。

4.4 影响因素分析

4.4.1 全局分析

通过对SHAP值按照特征维度聚合计算平均绝对值，得到样本集中最关键的5个特征，如图7所示。

图7 SHAP 平均绝对值最大的5 个特征Fig.7 Five features of maximum mean absolute value of SHAP

这5个特征分别为96号特征（29号节点处的负荷有功功率）、158 号特征（输电线路26-27 的有功功率）、161 号特征（输电线路12-13 的有功功率）、114 号特征（28 号节点处的负荷无功功率）、112 号特征（26 号节点处的负荷无功功率）。图7 中每个点代表1 个样本，横坐标为SHAP 值，SHAP 值越大则对预测结果的影响越大，正负号表示正向或负向影响，每个点的颜色越深则表示该特征的输入值越大。从图7 可以看出，这5 个特征的特征输入值越大，反而会对电压稳定状况造成负面的影响，并会增大电压失稳的风险。

以96 号特征为例，绘制特征输入值与该特征的SHAP 值间的散点图如图8 所示，以分析该特征的输入值对预测的影响。

图8 96 号特征的输入值与SHAP 值Fig.8 Input and SHAP values of Feature 96

从图8可看出，在96号特征（29号节点处的负荷有功功率）输入值小于270 MW时，对电压稳定的影响是正向的；当其大于270 MW时，则影响是负向的，并会增加电压失稳的风险。因此，将特征的输入值与SHAP值相联系，可进一步挖掘特征输入值与系统VSM间的隐含规则。在实际中，若29号节点处的负荷有功功率大于270 MW，则可以提示该负荷处于“警告状态”。类似地，对于其他特征也可以进行相同的分析。

另外，以96 号特征和158 号特征为例，绘制散点图如图9所示，以分析96 号特征和158 号特征对预测结果的影响。

图9 96 号特征与158 号特征对于模型预测的交互影响Fig.9 Interaction effect of Features 96 and 158 on model prediction

从图9可发现，96号特征即29号节点处的负荷有功功率在270～295 MW 范围内时，输电线路26-27 的有功功率越大反而会对模型预测造成负面的影响；当29号节点处的负荷有功功率超过295 MW时，输电线路26-27 的有功功率越大则更有利于维持系统的电压稳定。

4.4.2 个体分析

对于单个样本的分析，则以测试集中第1 个样本为例，训练样本的基准值为0.210 4，模型的预测值为0.071 6。各特征的特征输入值与SHAP 值如表3所示。

表3 各特征的输入值和SHAP 值Tab.3 Input and SHAP values for each feature

从表3可看出，单个样本中SHAP值最大的5个特征与全局分析中最关键的5 个特征并不一致。表3中96号特征对模型预测的正向贡献量最大，其特征输入值为264 MW，使系统的VSM 提高了0.083 1，其次是168 号特征。但是，173 号特征和158 号特征对于模型预测的负向影响最大，分别使系统的VSM降低了0.115 6和0.083 7。在所有特征的综合影响下，NGBoost模型的预测值为0.071 6。

因此，对单个样本进行个体分析，可以形象地了解到样本中的各个特征在该输入值下使得系统VSM升高或降低的具体数值。再结合全局分析，便可以进一步明确VSM 的降低或升高是由哪些特征的输入值偏高或偏低所造成的，进而可帮助调度人员及时发现安全隐患，有效保障电力系统的安全稳定运行。