应力诱发压电薄膜晶内微裂纹演化的数值模拟
2022-09-27王永璞黄佩珍
王永璞, 黄佩珍
(南京航空航天大学机械结构力学及控制国家重点实验室, 江苏南京 210016)
随着微机电集成器件的发展, 锆钛酸铅压电陶瓷(PZT)的研究重心从传统块体材料转向了薄膜结构材料, 然而PZT薄膜在制备过程中引入的气泡、孔洞等微观缺陷一定程度上限制了它们大规模应用。
Liu等[1]从热力学势能出发研究了力、电载荷对压电材料晶内孔洞形态演化的影响, 并对孔洞的形态演化路径和失稳条件进行了表述。Li等[2]考虑了小尺度效应, 通过所建立的非局域相场模型结合有限单元法与有限差分法研究了双压电基体中孔洞的形貌演化与迁移行为, 结果显示加载条件对演化具有显著影响。Li等[3]研究了压电薄膜中不同初始形状的夹杂在力、电载荷下的形貌演化和迁移行为。虽然上述研究中涉及对不同外场、位置下压电材料内部微观缺陷形貌演化的数值模拟, 但结果中只呈现了缺陷形貌在特定参数下的演化趋势, 并未揭示此类缺陷形貌演化的具体变化规律。
本文在蒸发-凝结和表面扩散下微结构演化的弱解描述[4]基础上建立应力诱发表面扩散下压电材料内部微结构演化的有限单元方程, 对各向同性PZT压电薄膜晶内微裂纹的形貌演化进行数值模拟, 重点关注应力载荷和微裂纹初始形态比对微裂纹形貌演化的影响。
1 基本理论
1.1 二维晶内微裂纹模型
图1所示为二维PZT薄膜单晶基体, 其内部存在一个位于晶粒中心的微裂纹, 并且在远场边缘承受均布拉压应力载荷σ0。PZT薄膜基体的长度和宽度分别为L和h, 椭圆微裂纹半长轴和半短轴分别为a、b。
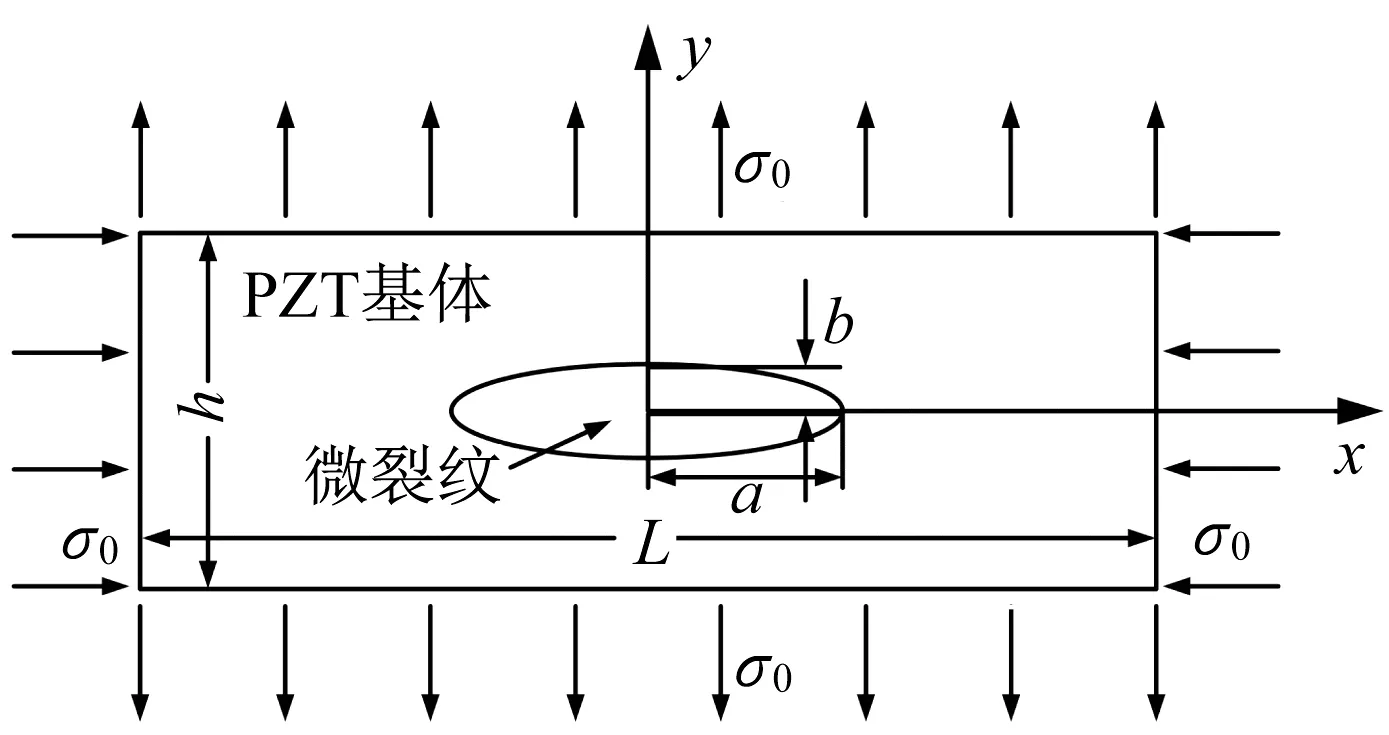
图1 PZT薄膜晶内微裂纹二维模型Fig.1 Two-dimensional intragranular microcrack model in PZT thin film
由于所研究的是晶内微裂纹, 且体扩散相较于表面扩散十分微弱, 因此仅需考虑微裂纹在表面扩散下的形貌演化行为。
1.2 弱解描述
固体材料表面上的原子(分子)通过表面扩散改变其位置并重新分布, 也通过蒸发-凝结与周围的气体环境发生物质交换。定义表面扩散的热力学驱动力F为单位体积物质在固相表面上迁移单位距离时系统自由能G的减少量。定义蒸发-凝结的热力学驱动力p为固相单位表面与气体环境交换单位体积物质时引起的系统自由能减少量。当上述2个过程同时发生时, 则有

其中,δG是表面虚运动引起的自由能增量,δI是与表面扩散相关的表面虚位移,δi是与蒸发-凝结相关的表面法向虚位移, ds代表自由表面的微分单元。
根据Herring的理论[8], 固体表面任意位置处表面扩散的物质通量正比于驱动力, 即

其中,M表示固体表面扩散的原子迁移率。
当系统处于接近平衡状态, 在单位时间内沉积在单位表面上的物质体积j与驱动力p成正比, 即

式(3)中m为蒸发-凝结过程中气、固两相之间的界面迁移率。
考虑到固相的质量守恒, 表面法向的虚运动位移与法向速度满足以下关系:
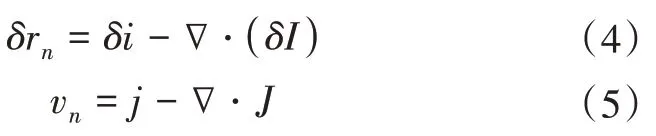
联立质量守恒关系与动力学定律即可获得包含蒸发-凝结与表面扩散的弱解描述, 即
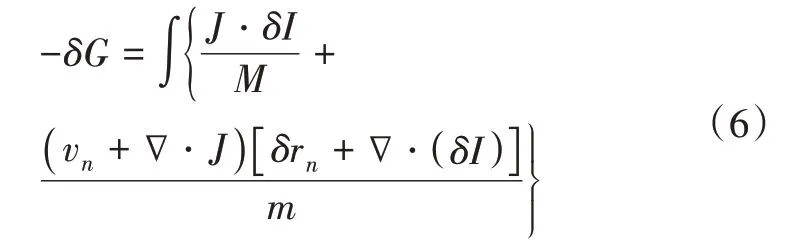
采用无量纲参数μ=mLe2M衡量蒸发-凝结与表面扩散之间的相对强弱, 其中Le表示最大单元的长度。当μ≪1时, 可以忽略系统中由蒸发-凝结造成的物质流出, 此时微裂纹表面形貌的演化仅由表面扩散机制控制, 且微裂纹表面积保持不变。
1.3 有限单元法
微裂纹表面可由图2所示的线性单元近似描述。其中单元倾角为θ, 单元长度为l。微裂纹-基体系统同时受到表面能和应变能的作用, 因此与线性单元运动相关的自由能增量可以表示为
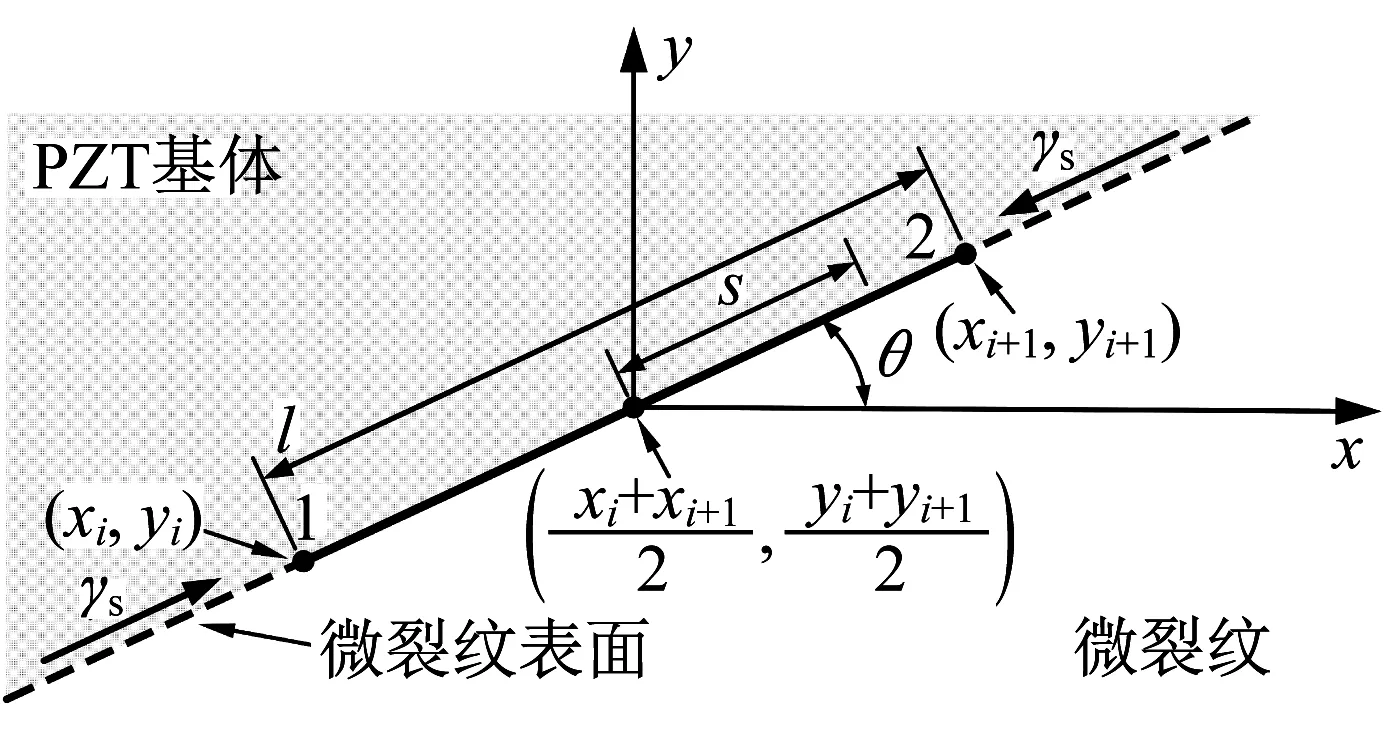
图2 微裂纹表面线性单元Fig.2 Linear element of microcrack surface
其中,γs为表面张力,ω为单元的应变能密度,δl为单元运动引起的单元长度变化。
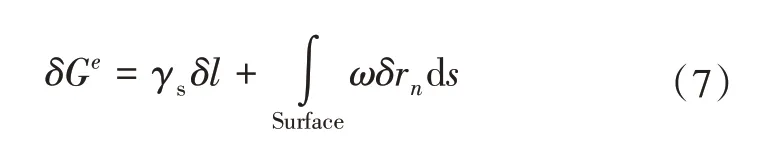
联立式(6)和式(7)并进行积分, 得到有限单元控制方程, 即

式(8)中,He为单元粘度矩阵,ẋe是单元广义速度矩阵,fe为广义载荷矩阵。
采用有限单元法对式(6)进行求解, 以获取各单元的节点速度, 通过设置一个微小的时间增量Δt即可计算出微裂纹表面节点的位移。随着时间的增加, 重复计算节点位移便可连续更新微裂纹表面的形貌变化。
2 可靠性验证
基于所推导的有限单元控制方程, 采用FORTRAN语言编制相应的有限单元程序。为验证程序可靠性, 考虑一个不承受外载的无限大各向同性基体中的椭圆形孔洞, Xia等[9]的工作中给出了该孔洞表面各位置在演化初始时刻法向速度的理论解, 即
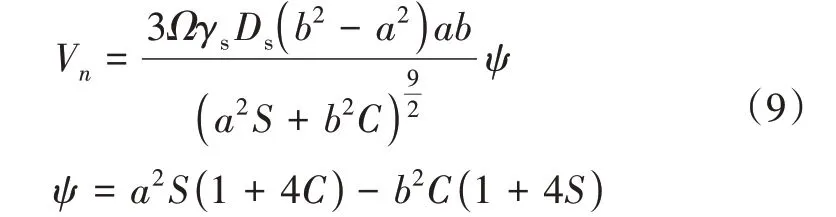
其中,S=sin2θ,C=cos2θ。
定义速度误差为
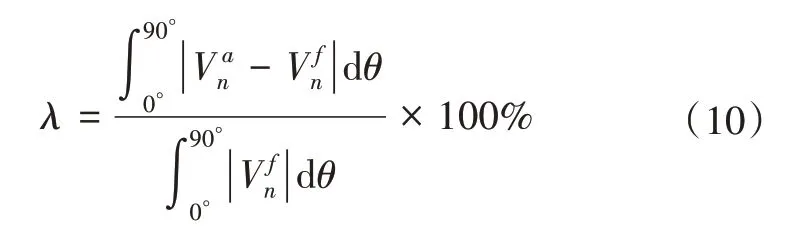
图3分别显示了有限单元程序计算所得的初始法向速度结果以及精确解结果。由图3可见, 数值解Vna与理论解Vn f吻合良好, 故本文的有限单元算法是可靠的。
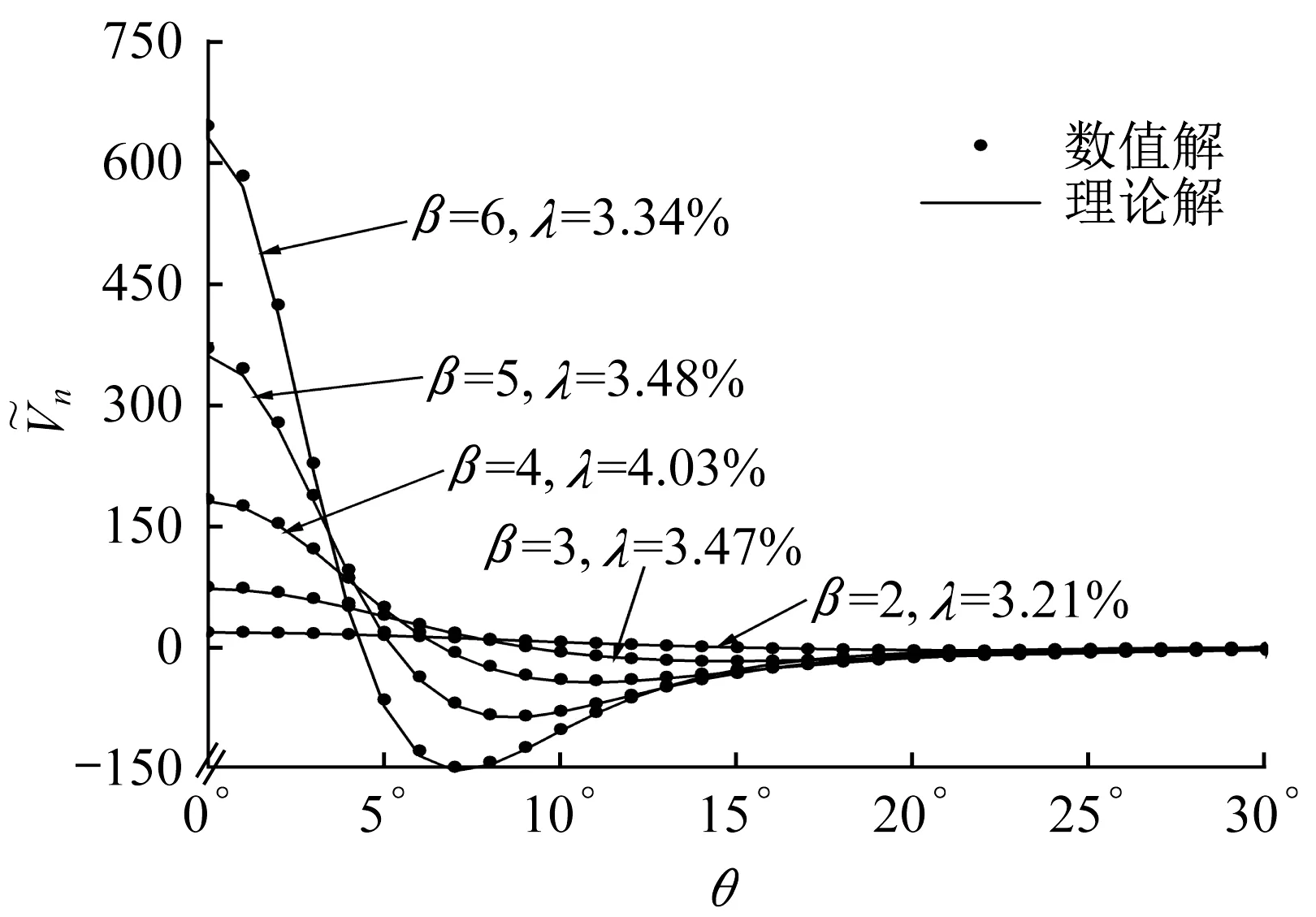
图3 表面初始法向速度理论解与数值解的比较Fig.3 Comparison between theoretical and numerical solutions of initial surface normal velocity
3 数值模拟与讨论
基于以上所建立的有限单元法, 本节对应力诱发表面扩散下PZT薄膜晶内微裂纹的形貌演化进行数值模拟, 并分析应力载荷及形态比对微裂纹形貌演化的影响。采用无量纲化应力载荷参数=σ0bγs, 无量纲化时间͂=tmγsb2, 形态比β=a b来描述微裂纹的初始形态特征。
3.1 应力对微裂纹演化过程的影响
图4显示了不同应力载荷下的PZT薄膜晶内微裂纹的演化过程。由图4可见, 微裂纹长轴端点在演化开始后存在向内收缩与向外延伸2种不同的演化路径, 在后续演化中表现为稳定演化和失稳分裂2种演化模式。在较小的应力载荷条件下[图4(a)], 表面能在演化驱动力中占据优势地位, 物质将在表面能驱动下沿微裂纹表面重新分布, 并“游走”至长轴端点附近区域, 长轴端点处由于物质的不断累积而向中心处坍缩, 微裂纹形貌逐步演化成近似圆形的稳定形态。当施加更大的应力载荷时[图4(b)和图4(c)], 微裂纹长轴端点附近应力集中加剧, 应变能驱动该处的物质向其他位置流动, 从而导致微裂纹在此处发生扩展。逐渐增大所施加的应力载荷, 微裂纹最终分裂为图4(b)所示的3个裂腔或图4(c)所示的5个裂腔。不同形态比β下微裂纹分裂时间s随应力载荷͂的变化如图5所示, 可见, 当β不变时,的增大会缩短分裂时间s, 即承载较大应力载荷的晶内微裂纹更不稳定, 其分裂速度更快。
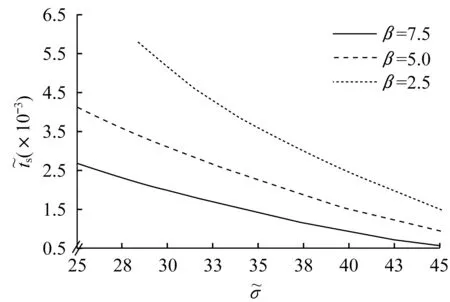
图5 微裂纹分裂时间s随应力载荷的变化Fig.5 Microcrack splitting time t͂s as a function of stress loading
3.2 形态比β对应力临界值c的影响
微裂纹的形貌演化过程伴随着表面能和应变能2种因素的相互竞争, 意味着在不同的应力载荷下并非都能发生分裂。大量的算例模拟表明, 应力载荷存在临界值c。当≤c时, 微裂纹演化为近似圆形的稳定形貌, 见图4(a);当>c时, 微裂纹分裂为多个裂腔, 见图4(b)和图4(c)。
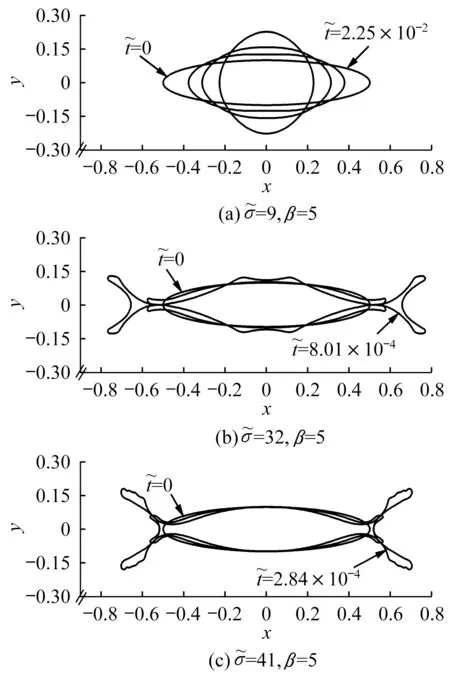
图4 β=5时, 不同下微裂纹形貌演化图Fig.4 Morphological evolution of the microcracksunder differentforβ=5
图6显示了应力临界值c随形态比β变化的情况。由图6可见,c随着β的增大而减小, 即增大β有利于微裂纹发生失稳分裂。

图6 应力临界值c随形态比β的变化Fig.6 Critical value of stress loadingc as a function of aspect ratioβ
4 结论
本文通过建立应力诱发表面扩散下PZT薄膜晶内微裂纹形貌演化的有限单元控制方程, 对微裂纹的形貌演化进行数值模拟, 得到以下结论:
(1)在应力迁移作用下, PZT薄膜晶内微裂纹存在稳定演化和失稳分裂2种演化模式。
(2)当微裂纹初始形态比不变时, 应力载荷存在临界值c。当≤c时, 微裂纹演化为近似圆形的稳定形貌;当>c时, 微裂纹分裂为多个裂腔。增大会缩短微裂纹失稳分裂所需的时间s, 促进微裂纹分裂。
(3)当微裂纹所承受的应力载荷不变时, 增大形态比有利于微裂纹发生失稳分裂。
