基于角度投影法的稀疏点云圆柱面拟合*

2022-09-27吴庆华李宗耀刘嘉程黎志昂

组合机床与自动化加工技术 2022年9期

吴庆华，李宗耀，刘嘉程，黎志昂

(湖北工业大学a.机械工程学院；b.现代制造与质量工程湖北省重点实验室，武汉 430068)

0 引言

在工业加工过程中，经常需要测量孔轴类零件的形位误差，用来检测装配质量。由于便携性与时效性强等特点，常用关节臂式坐标测量机[1]获取圆柱件精加工面的点云数据，用拟合圆柱面[2]的方法来获取孔轴类零件的几何参数，因此，圆柱拟合算法的效果直接影响孔轴之间形位误差评定的精度。

目前，圆柱拟合算法研究较多，传统的遗传算法[3]，特征值法[4]与均值漂移聚类方法[5]精度较高，但受限于圆柱的姿态和点云密度等问题，需要良好的初值来保证其运算的收敛性。事实上，曲线拟合的本质是非线性函数[6]迭代收敛得到最优解的过程，初值对拟合算法的收敛性影响很大，因而，初值的查找是拟合研究中的关键。ABDUL等[7]提出用主成因(PCA)法提取初值，在假定圆柱较长的情况下寻找圆柱轴线初值，但该方法对轴线方向相较于直径方向不长(即矮胖圆柱)的圆柱拟合效果不佳。RUI等[8]提出一种软投票(soft voting scheme)方法，在点云较为局部的情况下，消除了候选方向的歧义，粗查找出圆柱的姿态。但该方法受限于一些先验条件，如圆柱垂值于桌面。申旭[9]使用三点共线法，快速计算轴线方向的初值，但方法中的阈值常数在点云不均时需要人工选取，对点云密度要求高。

在飞机起落架各孔轴类零件的测量中，由于其点云具有姿态多，尺寸大和分布不均的特点，上述初值查找算法并不适用。受操作实效性的影响，采集的数据往往是稀疏的点云[10]，其局部特征不明显，容易对形位误差的检测造成误判。因此，初值的查找在该测量中更加关键。本文针对飞机起落架轴孔类零件测量时，用关节臂式坐标测量机采集的稀疏点云，提出了一种角度投影法来查找圆柱拟合的初值，利用圆柱的几何特性计算投影角度的范围，将最佳投影的初值代入圆柱拟合的误差方程，使其快速收敛得到最优解。

1 角度投影法初值算法模型

1.1 角度投影法数学模型

设有一个轴线为l的圆柱体，以及法线方向为n的平面，如图1所示。

(a) 圆形投影 (b) 非圆形投影

将圆柱投影到平面上，根据投影可以归为2种情形：

(1)轴线l与平面法向量n平行时，圆柱面投影到平面上是一个圆，该圆的半径与圆柱相等，圆心在轴线l上。

(2)轴线l与平面法向量n既不平行，也不垂直时，圆柱面投影如上图是个矩形加两个半圆组合的形状。

图1a中，当平面法向量与轴线平行时，该平面即为最佳投影面。理论上，圆柱的轴线在最小二乘意义上是通过其点云坐标重心的[11]。如图2所示设重心为p，p在圆柱内部。通过多个数据点与重心p连接线段的方向，在坐标系中计算角度范围，使的拟合圆柱的轴线l在该角度范围内。

图2 角度计算模型

1.2 投影范围计算

投影范围先是在原点处形成单位投影向量集为Φ={(Sxi,Syi,Szi)}，其中

(1)

这样单位向量集就会形成一个密集且均匀半球型，其中(Sxi,Syi,Szi)为单位向量的分量，如图3所示。

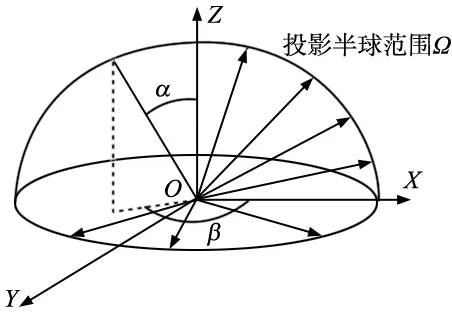
图3 投影方向示意图

其中，α、β代表投影线与z轴的角度，以及投影线投影到xoy面与x轴的角度。m1、m2代表着向量集的密度。然后计算出点云重心p，计算点云中每个点到重心的距离，选取多组距离长的线段lpl1,lpl2,lpl3…，由于轴类零件都为细长圆柱，选取角度最大的两组线段。记该两个线段为lpli,lplj，其中记lpli与z轴的角度为α1，投影到xoy面与x轴的角度记为β1。lplj与z轴的角度为α2，该线段投影到xoy面与x轴的角度记为β2。最后将角度范围(α1,α2)，(β1,β2)代入式(3)中，形成一定角度范围的投影方向。

1.3 初值计算

图4 投影点集与投影角度

(2)

(3)

计算当前投影圆的圆度，通过式(1)中的投影向量点集，在一定的角度内进行多次投影找出圆度最小的一组数据，找出F0的最小值，此时的投影方向(Sxi,Syi,Szi)，即为轴线的方向初值，由式(3)中的(d,e,f)求得平面圆心即为圆柱轴心线上的初始值点。

2 圆柱拟合算法实现

用角度投影法得到拟合的初值后，使用梯度下降法[12]进行圆柱拟合，获得目标圆柱参数的精确值。圆柱面可以看作到轴线相等距离的点集组成曲面，首先列出误差方程：

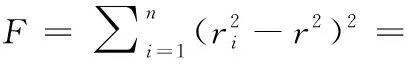
(4)

式中，Ai为数据点集坐标；ri为数据点集到轴线的距离；r为拟合圆柱半径；L为圆柱轴线方向；c为圆柱中心点坐标；I为单位矩阵。

然后对误差方程各个未知数分别求导，将第1.3节求出的圆柱参数初值代入各个参数方程，当误差函数F取最小值时，此时的轴线方向L，圆柱中心c和半径r，即为拟合圆柱参数的精确值。

3 实验及结果分析

3.1 标准圆柱拟合实验

为了验证该算法在不同姿态下拟合的效果，本实验在同一圆柱多种姿态下，进行数据的采集及拟合，来验证算法的有效性以及拟合精度。实验使用某公司的Quantum W系列6轴柔性三坐标测量臂采集数据，测量对象为金属圆柱件，其直径约为30 mm，长度约为300 mm。将圆柱件与关节臂固定到同一台面，共采集五组数据。为了验证特殊角度下的拟合效果，前三组的圆柱轴线分别与x,y,z轴平行，另外两组为自由摆放，如图5所示。

图5 实验对象不同姿态示意图

由于圆柱体表面大都经过磨削加工，为排除粗差对结果的干扰，用叶序理论[13]采点时误差较小，在圆柱件上记上标记点，使采集的测量点呈螺旋状，如图5中左上图所示。采点时，用Faro测量臂的探针，依次接触圆柱件上的标记点进行取点，共计20个点。按照本文方法计算该圆柱件的直径与轴线方向的单位向量，并将结果与文献[9]中使用的SA商业软件进行对比，计算结果如表1所示。

表1 不同姿态圆柱拟合结果对比

从表1实验结果可以看出，在不同的摆放姿态下，采集的稀疏点云均拟合成功，没有出现非线性迭代计算中的发散或者陷入局部收敛的情况。在轴线方向的计算结果中，本文算法与SA软件结果均保持一致。在圆柱直径拟合的结果上，本文算法与SA软件平均误差：Uv=0.005 mm，最大误差：Umax=0.009 mm，由此可以看出，其精度可达到SA软件的水平。

为了进一步验证本文算法对大直径矮胖圆柱的拟合效果，采用文献[3]中的实例数据进行计算，用遗传算法测量卷板辊这种大型圆柱工件的直径，并与本算法进行对比，结果如表2所示。

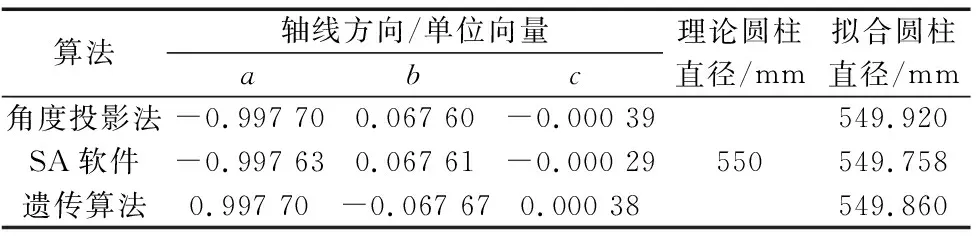
表2 不同算法拟合结果对比

表中3种方法拟合的结果相近，说明本方法针对大直径矮胖圆柱的稀疏点云拟合也能达到较高精度。

3.2 飞机起落架前后轮轴平行度测量实验

实际实验在飞机起落架综合测量平台上进行。选取某型号飞机的起落架仿件作为测量对象，以关节臂式三坐标测量机作为测量工具，采集前后轮轴点云数据进行圆柱拟合，将拟合的圆柱参数应用于前后轮轴平行度的评定。实验现场如图6所示。

图6 实验平台

该起落架仿件前轮轴直径约为φ54 mm，后轮直径约为φ79 mm，轴长约为1200 mm，两轴相距约为1400 mm。由于加工面较短，实验在每个加工面采集10个测量点，每个轮轴有两个加工面，共采集40个测量点。根据国标规定，轴与轴之间的平行度可以用最小区域法[17]求得。当给定任意方向时，轴线之间的平行度误差为包围误差区域最小外接圆的直径，该直径即为最终误差。由于涉及到形位误差的评定，将实验结果与工业测量软件InnovMetric进行对比，测量点数据如表3所示。

表3 飞机起落架前后轮点云数据

表4中平行度误差测量结果与软件相差0.059 mm，由于与InnovMetric软件存在平行度评价的差异，对于起落架这种大尺寸零件的测量，其结果误差在接受范围之内。并且前后轮轴轴线方向和直径拟合结果与InnovMetric相近，能有效验证该算法在起落架形位误差测量中的实用性与准确性。另外在实验中发现，针对细长且分布不均匀的稀疏点云，InnovMetric软件在拟合时有时会出现轴线偏离的现象，导致拟合失败。而本算法均拟合成功，说明角度投影法收敛性较好，适应此类圆柱的拟合。