基于快速超扭曲算法的永磁同步电机预测控制*

刘 伟，吴润龙

(东北石油大学电气信息工程学院，大庆 163319)

0 引言

永磁同步电机(permanent magnet synchronous motor,PMSM)因具有效率高、可靠性能强和功率密度大等显著优点而被广泛应用于新能源电动汽车、风力发电、数控机床、伺服控制等诸多领域[1]。尽管永磁同步电机具有诸多优势，但其仍然是一个多变量、强耦合和非线性的复杂系统，对控制系统的设计提出了很高的要求。传统矢量控制的转速环和电流环都是通过PI控制完成的，但经典的PI控制并不能够使PMSM表现出高品质的动态性能、高精度的稳态性能和抗干扰的强鲁棒性能，难以满足高精尖领域下的工作要求。因此，国内外大量的专家学者提出了许多先进的PMSM控制方法，如滑模控制[2]、预测控制[3]、自抗扰控制[4]、内模控制[5]等。这些控制方法在应用于PMSM控制系统中，取得了很多的研究成果。

PMSM控制系统在引入预测控制后，无差拍电流预测控制(deadbeat predictive current control,DPCC) 逐渐成为主流的电流环控制方法。王宏佳等[6]提出了一种改进无差拍电流预测控制算法，在系统电感参数发生变化的情况下仍能获得良好的动稳态性能。王庚等[7]详细分析了DPCC算法在电机参数不匹配时导致的电流静差问题，并提出一种在电感及磁链参数变化时的电流静差消除算法。仝淼等[8]针对DPCC易受模型失配而产生电流静差的问题，提出了一种具有延迟补偿的改进DPCC控制方法，此算法在PMSM电感、电阻与磁链失配时，能够抑制因参数失配而引起的电流静差，以提高对电流环的精确控制程度。

为了进一步提高控制效果，在电流环采用DPCC控制方法下，任志玲、齐歌等[9-10]在速度环中引入模型预测速度控制，但预测控制本质上仍是依赖于系统模型参数的控制策略，鲁棒性较差。而滑模控制方法具有较强的鲁棒性，其具有抗扰动能力强，计算量小且易于实现等优势，但传统滑模控制却存在较大的抖振，影响了系统的稳态精度。RATH等[11]介绍了一种二阶滑模超扭曲算法(简称STA)，此控制算法不仅输出的控制信号连续无抖振，且具有较强的鲁棒性。张庆超等[12]在转速环中将传统STA算法加入比例项构建出快速STA算法，提高了系统的响应速度。淡宁等[13]用快速STA和STA算法分别设计速度环和电流环，实现了双环二阶滑模控制，提高了系统的鲁棒性。

本文以上述文献的研究成果为基础，继续探寻PMSM控制系统获得高品质的动、稳态性能和强鲁棒性的方法。本文将快速STA与DPCC控制算法相结合，其中二阶滑模快速STA算法应用于转速环，DPCC应用与电流环。同时为了提高系统的鲁棒性，设计了扩张状态观测器来补偿系统的外部扰动。最后通过MATLAB/Simulink仿真平台，验证和对比了本文所提方法的可行性和有效性。

1 无差拍电流预测控制

本文以表贴式PMSM为研究对象，其在两相同步旋转坐标系下的数学模型为：

(1)

(2)

(3)

(4)

式中，ud、uq、id、iq分别为永磁同步电机d-q轴定子电压和电流；Rs为定子电阻；Ls为交直轴电感；ψf为永磁体磁链；Pn为电机极对数；Jm为转动惯量；Bm为摩擦系数；Te为电磁转矩；TL为包含电机空载损耗在内的负载转矩；ωe为电机的电角速度；ω为转子的机械角速度，其中ωe=Pnω。

以表贴式PMSM的电流作为系统的状态变量，其状态空间方程可根据式(1)、式(2)表示为：

(5)

当系统的控制周期Ts非常小时，PMSM的反电动势D与输入端的控制电压u在一个控制周期kTs到(k+1)Ts之间可近似认为恒定不变。控制系统的电流预测模型，可通过对状态方程式(5)的离散化求解获得，表达式为：

i(k+1)=F(k)·i(k)+G·u(k)+M(k)

(6)

根据DPCC的基本原理，以当前时刻转速环的输出值作为下一时刻PMSM电流环的控制指令值i*(k+1)，并将其与PMSM电流采样获得的当前电流状态值i(k)带入式(6)。通过式(6)即可计算出所需电压矢量u(k)，表达式为：

u(k)=G-1·[i*(k+1)-F(k)·i(k)-M(k)]

(7)

2 基于快速STA的速度控制器设计

将式(4)代入式(3)得：

(8)

本文的PMSM速度环控制算法将以STA为基础进行设计，如式(9)所示：

(9)

通过在STA 中加入比例项可构造出快速 STA，能够有效提高系统的收敛速率，其表达式为：

(10)

式中，α、β、γ为控制器的正常数增益。其中，α和β用于保证系统在有限时间内稳定、减小抖振以及抵抗不确定因素的影响；γ用于提高系统的收敛速率。

令x=ω*-ω，结合式(8)，建立PMSM的转速误差状态方程为：

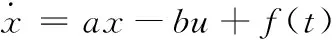
(11)

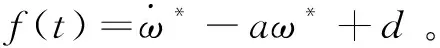
选取滑模面为：

s=x=ω*-ω

(12)

结合式(11)、式(12)得：

(13)

将式(10)代入式(13)得：

(14)

式中，α′=bα；β′=bβ；γ′=bγ-a。

(15)

由式(14)可知，即使不知道系统模型的准确参数，也只需要对α、β、γ进行调节即可。

3 扩张观测器的扰动估计

由式(8)可以看出，PMSM控制系统包含了扰动项d，其具体数值无法通过测量直接获得，因此本文设计了一种扩张观测器来估计系统的扰动值。

3.1 扩张观测器设计

建立系统的状态方程，令状态变量x1=ω，输出y=ω，由式(8)可得：

(16)

将扰动项d扩张为新的状态变量x2，设其一阶导数为Θ(t)。由此建立系统状态空间方程为：

(17)

以x1和x2为观测对象，建立转速估计误差e的高增益反馈，设计扩张扰动观测器为：

(18)

3.2 观测器稳定性分析

利用李雅普诺夫稳定性理论对观测器的稳定性进行分析，通过建立观测器的误差状态方程，证明其在有限的时间内可以收敛。

定义观测器的误差状态变量为：

η=[η1η2]T

(19)

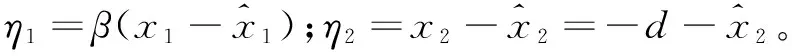
因为：

(20)

(21)

因此，扩张观测器的误差状态方程可表示为：

(22)

矩阵A的特征方程为式(23)：

(23)

ATP+PA+Q=0

(24)

定义观测器的李雅普诺夫函数为：

(25)

对式(25)V进行求导，结合式(24)可得：

(26)

假设扰动导数Θ(t)有界，即|Θ(t)|≤L，结合式(26)可得：

(27)

(28)

由式(28)可见，β越大系统越容易收敛。

4 仿真及结果分析

为了对本文所提控制算法的正确性进行验证，在MATLAB/Simulink平台下，搭建出基于快速超扭曲算法的永磁同步电机预测控制仿真模型，具体的控制结构框图如图1所示。其转速环为快速STA算法，电流环为无差拍电流预测控制，使用扩张状态观测器(DOB)来补偿系统的外部扰动以提高鲁棒性。仿真实验所用的PMSM具体参数如表1所示。

图1 PMSM控制系统结构框图

表1 表贴式PMSM参数

为了验证本文提出的基于快速超扭曲算法的永磁同步电机预测控制(简称本文方法)效果，将其与模型预测(MPC)速度控制+无差拍电流预测控制(简称方法1)和快速STA速度控制+STA电流控制(简称方法2)的仿真结果进行对比。基于方法1的仿真中，MPC速度环的柔化系数α1=0.988，加权系数λ1:β1=1100:0.02；基于方法2的仿真中，快速STA速度环控制器的参数为α=3.8，β=100，γ=0.001；STA电流环的参数为ki1=100，ki2=80；基于本文方法的仿真中，快速STA速度环控制器的参数为α=1.5，β=100，γ=0.11，观测器参数为ε1=1.6×105，ε2=109。

4.1 电机空载启动仿真

图2为当给定转速为1000 r/min时，3种控制算法下永磁同步电机对应的空载转速响应波形图；图3为其转速稳定时的局部放大图。从图中可以看出，在方法1的控制算法下，转速虽能实现无超调响应，但达到稳速的时间较长，在稳速下的转速跟踪误差为-0.015～0.015 rpm；在方法2的控制算法下，转速响应波形有明显的超调，且经过多次震荡后才能达到稳速，在稳速下的转速跟踪误差为-0.04～0.04 rpm；在本文所提出的控制算法下转速无超调，且能够最快到达稳速状态，在稳态下的转速跟踪误差最低，仅为-0.01～0 rpm，成功削弱了抖振。对比另外两种控制算法可以看出，本文方法不仅拥有快速的动态响应能力，而且有着更高的稳态精度。

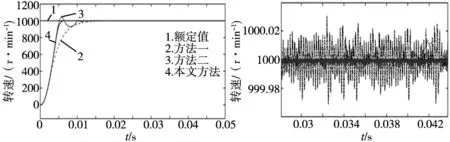
图2 3种控制方法下的转速仿真曲线 图3 转速稳定时的局部放大图

4.2 电机定速下的加减载仿真

当电机在空载状态下以1000 r/min的恒速状态运行时，在0.03 s时突加5 N·m的负载，并在0.05 s处卸掉负载。图4为负载扰动下3种控制方法对应的转速响应图，图5为突加载时的转速局部放大图，图6为突减载时的转速局部放大图。从图4～图6中可以看出，在突加减相同负载扰动的情况下，使用方法1控制下的电机转速变化最大，且转速恢复至给定值所需时间也最长，抗扰性能较差。在方法2的控制下，电机转速变化虽然不大，转速恢复至给定值所需时间也较短，但转速恢复过程中存在多次震荡的环节，抗扰性能不强。使用本文所提控制方法时，电机转速变化最小，转速恢复至给定值所需时间也最短，且不存在震荡环节，因此本文所提算法具有更好的鲁棒性，提高了控制系统的抗干扰性能。

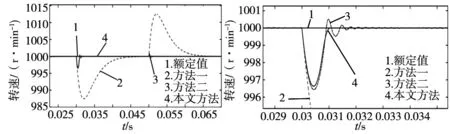
图4 负载扰动下3种控制方法对应的转速响应图 图5 突加载时的转速响应图

图6 突减载时的转速响应图

此外，从图7中3种控制方法下的转矩响应图可以进一步看出，在突加减相同负载的情况下，本文所设计的控制方法表现出更加优良的控制性能。

图8为本文所设计的扩张状态观测器对负载扰动进行实时估计的波形图。从图中可以得出，观测器对突加减负载的观测较为平稳，且能够快速收敛于实际值，说明了本文所设计观测器的有效性。

图7 3种控制方法下的转矩响应图 图8 观测器的估计结果图

3种控制方法所对应的电机控制性能的动静态参数如表2所示，从表中可以得出，本文所提出的基于快速超扭曲算法的永磁同步电机预测控制方法与文中的另外两种控制方法相比较，具有更快的响应速度，更低的稳态误差，更强的鲁棒性能。

表2 3种控制方法下PMSM的仿真结果

4.3 电机带负载启动下的变速仿真

为了进一步验证控制系统在带负载情况下的变速性能，使系统带5 N·m负载启动，系统仿真时间设置为0.06 s。初始期望速度设置为800 rpm/min，在0.03 s突变为1200 rpm/min，实现了PMSM在中高速范围内的带载运行，图9为对应的仿真图。从图中可以看出，在全程带负载情况下，即使面对系统突然加速的情况，本文所设计的控制方法与方法1和方法2对比表现出了优异的调速性能，且全程无超调，进一步证明了本文方法的可行性与有效性。

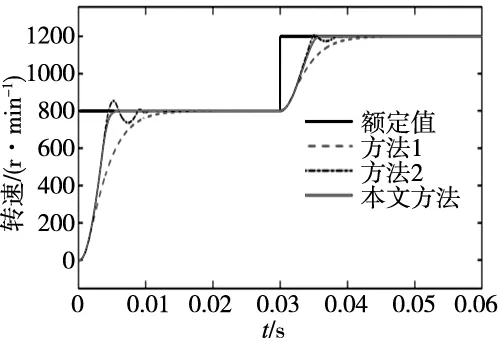
图9 电机带负载时的变速仿真图

5 结论

快速的动态响应能力、更高的稳态精度与更强的鲁棒性能是高性能电机系统必备的品质。本文针对在方法1的控制方法下响应速度慢，抗干扰能力差和在方法2的控制方法下转速有超调，且调节过程中存在多次震荡的问题，提出了基于快速超扭曲算法的永磁同步电机预测控制。此控制方法在速度环采用二阶super-twisting滑模控制，电流环采用DPCC控制方法，同时引入了一种扩张状态观测器来观测系统的扰动值。与前两种控制方法相比，本文提出的方法转速响应速度快，稳速时控制精度高，成功削弱了系统的抖振，且抗负载扰动能力更优。仿真结果证明了此控制方法的可行性与有效性。