基于图像处理的3D打印模型弦公差优化研究

2022-09-27谭礼健

内燃机与配件 2022年15期

0 引言

目前最常见的3D打印技术就是熔融沉积成形技术(Fused Deposition Modeling，简称为FDM)，FDM技术最早是由美国的Scott Crump博士于1988年研制成功，它具有材料低成本、利用率高、成形速度快、设备小巧、操作简单、可以加工任何复杂模型、支撑结构易剔除等优点而被广泛应用在建筑模型设计、医疗器具生产、航空航天器零件生产等领域

。在实践打印过程中，FDM3D打印通过分层构建来直接制造具有复杂几何形状的零件。通常在大多数三维建模过程中，采用的一般方法都是首先创建一个三维实体模型，转换成立体光刻(STL)文件格式，然后通过组成STL模型的三角面片与切平面相交生成二维平面轮廓线

，最后通过切片软件的工艺设计和后处理完成FDM3D打印全过程。

详细的说，在常见的FDM-3D打印过程中，我们使用切片软件(CURA)对待打印的STL模型文件进行处理，通过工艺参数的设置获得3D打印设备能够识别的G-CODE,从而控制喷头按照轨迹逐层叠加，最终获得我们在NX12.0软件上构建的模型。但在使用建模软件导出为STL格式的界面上，软件会让设计者填写弦公差与角度公差

两个参数，弦公差就是弦与真实曲面之间的最大距离，角度公差就是指相邻弦之间的最大角度。可以这样理解：在设计好PRT模型后，需要人工的调整模型文件中涉及的非直线特征的拟合程度，通过类似插补的原理在规定的打印精度下实现曲面特征的直线化。

在本文的研究中，基于职业院校中机械类专业的1+X复合车铣项目中的标准轴承(牌号：16004)首先运用NX12.0软件构建Ø20×8的模型，在控制角度公差不变(恒定等于18度)的情况下，试验研究理论弦公差在0.01—1之间，工业软件NX12.0对PRT文件转化成STL文件后真实弦公差情况，利用简化数学模型理论推算不同理论弦公差下的弦长公式和平面面积公式，最后通过FDM-3D打印该理论弦公差模型下Ø20×8的零件，借助1+X复合车铣项目中的标准轴承(牌号：16004)为定位夹具，通过图像处理技术判断其精度的变化规律,并找出在实际打印教学环节，综合性能最优的弦公差参数值。

当前，世界政治多极化和经济全球化的进程加快，西方敌对势力极力通过多种途径对我国进行意识形态领域的渗透。国内，随着改革开放进一步深入和信息技术的迅猛发展，人们的行为习惯、思维方式和价值观念都发生重大变化；国内各种敌对势力利用各种机会和场合抹黑党和政府，制造和散布各种反动言论。这些复杂、多变的趋势和形势，给一些中小学思想政治课教师造成迷惑。

1 理论模型

1.1 边界条件

在研究的模型中，16004牌号的深沟球轴承内圈直径为20mm，外圈直径为42mm，轴承厚度为8mm。因此在本次研究主题3D打印模型中，将Ø20×8的圆柱体在笛卡尔坐标系下，我们可以将其近似看作平放在XOY平面的二维轮廓的圆平面，通过研究3D打印的二维平面图形的面积与16004轴承内圈理论面积的差值来判断其建模软件设定的理论弦公差对FDM3D打印模型精度的影响。

1.2 平面圆的弦公差模型(如图1)

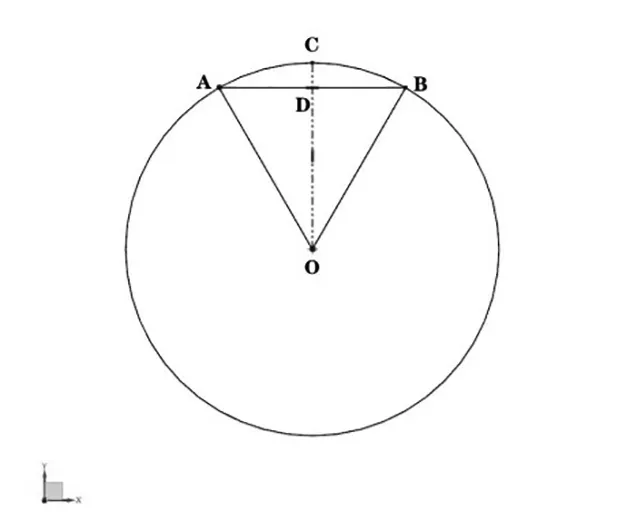
设

若：正

变形周长为

,则

在3D打印前处理过程中,我们希望我们的曲面特征被完全保留，也就是n为无穷大

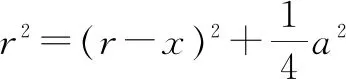
(1-1)

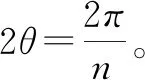
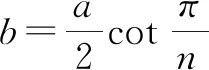
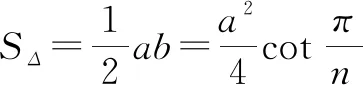
则有:

所以正

变形面积也可以写为：

(1) 德泽乡温泉特征明显，温泉出露较为集中，偏硅酸等有益元素含量较高，溢出带均位于南北向务德断裂F3上，且靠近断裂带附近温泉温度较高，该断裂为德泽盆地内的主干断裂。

民办高校仍有相当部分科研水平薄弱，缺乏企业工作经历，没有负责或参与过产品的研发和改进，因而对于大部分尤其是一毕业就进入高校工作的青年教师来说，在双创教育方面没有足够多的实践历练和心得体会，导致难以胜任双创教育工作。

女人吸掉半包摩尔烟时，天光跟着就暗了些，也有不少人站起身离开咖啡馆，女人不时地看腕上的手表，想何时给自己叫东西吃。

根据勾股定理：

“妈的，家里还有八十岁的老娘等老子送终呢，老子当然死不得，死不得。”赵锡田拂了拂衣袖，猫进临时指挥所。

所以当n→∞时：

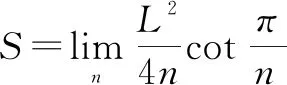
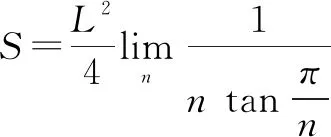
多项研究提示趋化因子及其受体网络在外周及中枢神经系统中的重要作用。就趋化因子的多重作用而言，包括大脑发育、神经可塑性、细胞间通信、神经传递、神经内分泌功能、炎症过程及行为的调控，趋化因子可能会被认为是治疗抑郁症及精神疾病有吸引力的生物标志物。然而各项研究结论存在矛盾，主要由于诊断及纳入标准不一致、检测手段及研究方法不同等，期望未来工作可以更深入地研究趋化因子在大脑中的作用，进而为临床诊疗提供新思路。

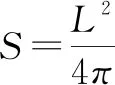
a假定PRT文件转化为STL文件后，平面实际轮廓为正多边形。

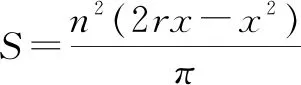
(1-2)

后来，新的一代成了全镇的骨干和精神，学画的学生们也长大成人，渐次离开了，她们没有让她们自己的女孩子带着颜色盒、令人生厌的画笔和从妇女杂志上剪下来的画片到爱米丽小姐那里去学画。最后一个学生离开后，前门关上了，而且永远关上了。全镇实行免费邮递制度之后，只有爱米丽小姐一个人拒绝在她门口钉上金属门牌号，附设一个邮件箱。她怎样也不理睬他们。

(其中：

为多边形的边数；

=10mm；

为理论弦公差)

2 试验过程

2.1 试验设备与材料

(1)实验设备：

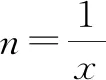
打印设备：本课题选用的FDM3D打印设备为太尔时代工程级桌面3D打印机UP 300。它的成型尺寸为 205 X 255 X 225 mm；理论成型精度为±0.1/100mm，打印材料为直径1.75的PLA材料。

(2)图像设备：机器视觉是人工智能正在快速发展的一个分支，一般包括光源、镜头和相机，它是用机器代替人眼来做测量和判断，在大批量重复性工业生产过程中，用机器视觉检测方法可以大大提高生产的效率和自动化程度；本次试验使用的图像设备包含：300 X 300 X 300 mm的镜面工作平台，

2017年12月，试验样机现场安装后，运行期间观察集成清扫装置的使用效果，并检测了硫磺粉尘浓度，结果见表7。

1200万像素图像处理摄像头以及一套控制软件与设备。

2.2 试验假设与准备

(1)试验假设

将公式(1-1)代入上式由此推得在理论弦公差下二维平面圆轮廓包围下的多边形面积为：

b在FDM3D打印零件后，Ø20×8高度方向的轮廓由平面二维轮廓平行延伸所得。

(2)试验准备

在利用图像识别技术计算平面二维轮廓的面积之前，我们要明确在工业软件NX12.0中(默认18°角度公差的情况下)，弦公差从0.01—1之间，平面轮廓实际产生的三角形个数，与理论计算三角形个数的规律，才能进一步探讨在18°确定的角度公差下，设置不同的弦公差，对实际模型打印效果的精度影响。如表1所示：从NX12.0中，分别设置展示了弦公差从0.01-1之间，理论三角形个数，通过测试我们发现，NX实际的的三角形个数为理论计算条件下的三角形个数和18°角度公差下的三角形个数求交集所得，特别的：在本次测试的弦公差范围内，0.13—1之间的弦长公差下，三角形个数均为20。

2.3 试验方案

基于NX12.0工业软件的实际求解结果，运用公式1-2中多边形面积理论模型规划以下两个试验方案，表2中，通过设定NX12.0软件中弦公差，获得理论内接正多边形个数，同时推算理论弦公差，与理论多边形面积。通过和理想圆面积的比较，获得NX12.0中通过设定0.01—1之间的弦公差，理论上FDM3D打印的效果变化情况。

此外，利用图像处理设备，在设备成像平台，使用16004牌号的深沟球轴承定位夹具，计算出设备捕捉的面积S3,在NX12.0软件设定公差0.01-1之间，比较捕捉面积S3与理论多边形面积差值的绝对值，从而获得图像处理识别面积与理论模型的差异，求证理论多边形面积计算模型的精度，同时验证图像处理设备的捕捉精度能否用于批量化单一重复检测环节。

划痕实验及Transwell小室法结果显示，与对照组比较，SCC-15细胞中过表达miR-219能降低SCC-15细胞的迁移及侵袭能力。然而，当共转染miR-219和PRKCI后，SCC-15细胞的迁移能力比单独转染miR-219的SCC-15细胞降低了50%以上(P<0.01)，SCC-15细胞的侵袭能力比单独转染miR-219的SCC-15细胞降低了50%以上(P<0.05)。说明由于PRKCI的过表达，逆转了miR-219抑制肿瘤迁移及侵袭能力的作用(图2E，图2F)。

1.2.1.1 成立干预小组干预小组由取得心理咨询师资格证的副主任护师2名和主管护师2名、工作2年以上的护师4名组成。研究开始前对小组成员进行研究内容、研究流程及研究方法等统一培训。

3 试验结果

3.1 理论模型验证

确定了以上试验假设和试验准备环节，针对实验方案中表二进行试验研究，其中需要说明的是：因为在二维圆平面轮廓中，内接正多边形的边数和内接的等角三角形个数相等，因此在表1中NX的实际三角形个数就等于正多边形的边数；同时，在表1中，尽管弦公差从0.01—1进行变化，但是三角形个数变化区间为20—72，因此在不影响本文研究的情况下，我们在实际试验方案制定的过程中仅使用内接正二十边形到内接正七十二边形的二维平面进行理论计算和基于图像处理的试验研究，此外，在设定的弦公差为0.13-1之间，理论二维圆轮廓的内接正多边形都为20(如图3、图4所示)，因此，在试验结果部分弦长公差并不是线性变化。最后，试验方案获得结果如表4所示：

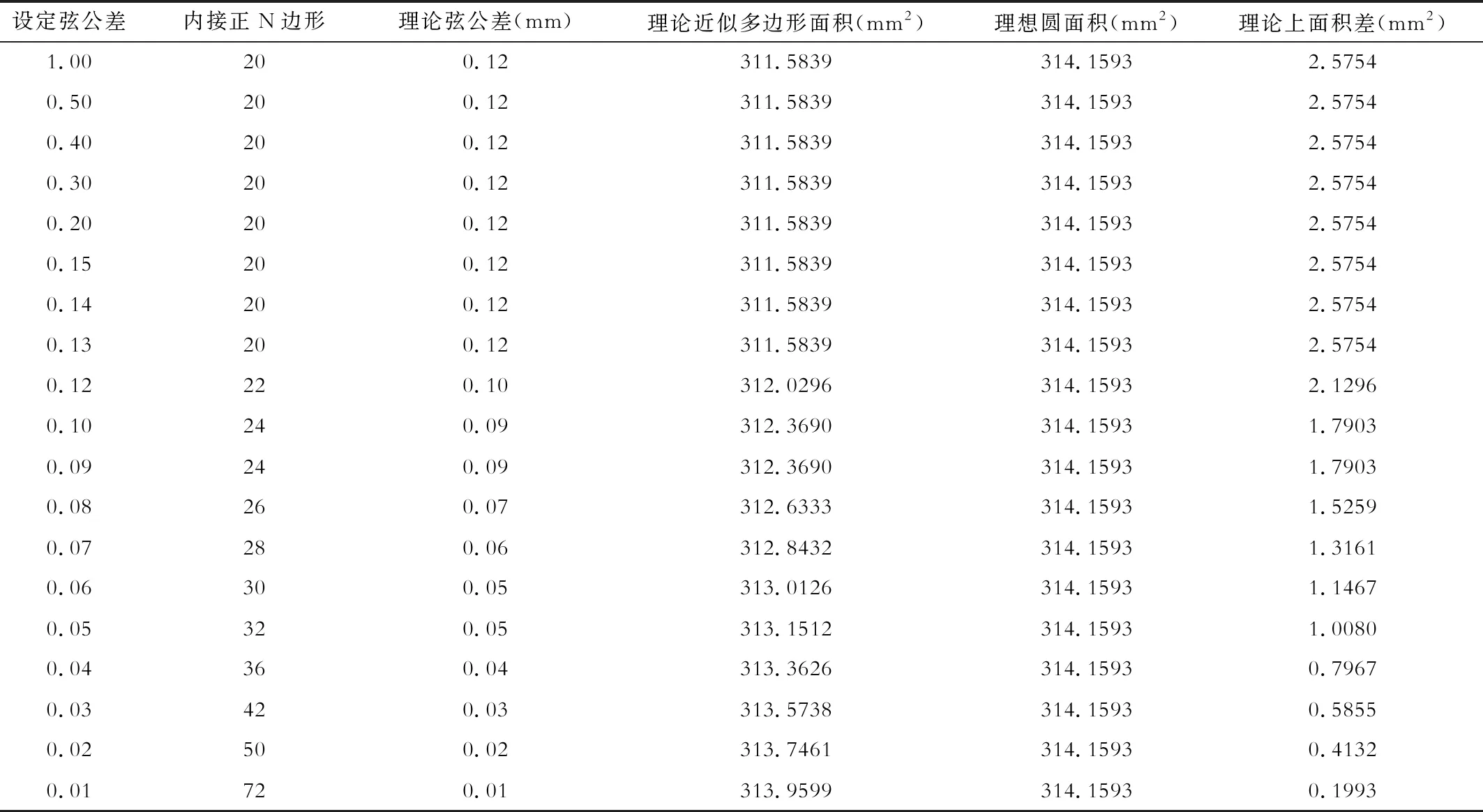
通过查表，设定弦公差在0.01-1之间变化过程中，随理论模型计算的面积与理想二维轮廓的面积差值之间的变化规律如图5所示：

从图5五中可以看到，在NX12.0软件中设定的弦公差从0.01-1的变化过程中，理想圆平面的面积(S2)和理论模型计算的多边形面积(S1)的差值在设定弦公差为0.01-0.12之间是一个近似线性的递增关系，其中理论模型计算的多边形面积从313.959mm

下降到 312.029mm

；S2-S1从0.199mm

线性递增到2.129mm

。但当设定弦公差等于0.13-1时，由于NX软件中角度公差(本文恒定为18°)的影响，使得在该区间内，理论模型计算的多边形面积S1恒等于311.58mm

；S2-S1的差值也恒等于2.575mm

3.2 图像处理设备验证

使用NX12.0软件建立Ø20×8模型，导出STL模型文件中，设定控制角度公差18°，分别导出弦公差0.01-1之间的19组STL 文件，在FDM3D打印设备中按照系统默认打印参数进行增材制造，冷却相同时间后，放置于图像处理设备并用16004深沟球轴承内圈进行定位(如图6所示)，并计算拍照面积(S3)，最后将图像处理设备拍照面积S3和理论模型计算的多边形面积S1的差值取绝对值，得到表5。