基于广义正规变化尾的卷积展开式及其应用

季海波， 王 丽

(宿迁学院 文理学院，江苏 宿迁223800)

1 预备知识

定义1[4]设f:R+→R+为可测函数，若存在α∈R，对任意的x>0，有

则称f是正规变化的，记作f∈VR(α),α为正规变化指数.

定义2[7]设f:R+→R+为可测函数，若存在α∈R，且α≠0，函数a(t)>0，使得对任意的x>0,有

2 尾分布为广义正规变化下的卷积展开式

定义2中的f(t)与a(t)存在如下关系[8]：若f∈VGR(α,a(t)),则当t→∞时，

引理2[9]f:R+→R+是L可测的，则f是广义正规变化的当且仅当∃α∈R,α≠0,a(t)∈VR(α)，且

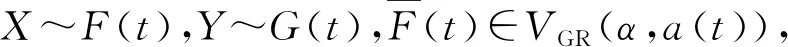
定理1设X～F(x),Y～G(x)，且满足

Ⅲ)E(X)<∞,

N为足够大的正整数.

证根据卷积公式,当x>0时，有

(1)

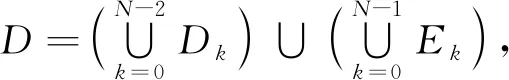
图1 区域D的分割

先计算概率P{(X,Y)∈Dk}，k=0,1,2,…,N-2.

由条件Ⅰ)，Ⅱ)及引理3，有

(2)

(3)

因此，由引理2及(2)，(3)式，可得

由引理1，当x→∞时，有

(4)

再计算概率P{(X,Y)∈Ek}，k=0,1,2,…,N-1.

由条件Ⅲ)，有

从而有

(5)

将(4)，(5)代入(1)式，可得

(6)

其中

推论1设随机变量X～F(x),且满足定理1中的条件Ⅰ)，Ⅲ)，则

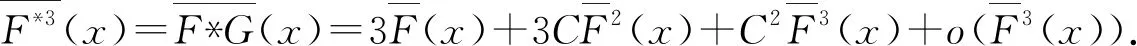
3 卷积展开式在C-L模型中的应用

破产概率作为评价保险公司综合保费与索赔过程的稳健性的重要指标，是风险管理的有用工具.破产概率的计算是精算学里非常经典的问题，C-L模型给出了具体表达式[3]：

(7)

1)F(t)∈VGR(α+1,ta(t))，x≥1;

2)F(t)∈VGR(α,ta(t))， 0

引理6设X～F(x),Y～G(x)，且满足下列条件：

c)E(X2)<∞，

N为足够大的正整数.

引理7设随机变量X～F(x),且满足引理6中的条件a)，c)，则

(8)

证将(8)式代入(7)式，有

整理可得结论.