武汉城市圈县域经济体第一产业发展的技术效率分析

刘 迅，何梦琪

（湖北经济学院，武汉 430205）

一、引言

自2007年12月国务院正式批准武汉城市圈为“全国资源节约型和环境友好型社会建设综合配套改革试验区”以来，武汉城市圈的经济取得了巨大的发展。仅以武汉城市圈的县域经济体①发展为例，在2009-2019年的11年间，36个县域经济体的地区生产总值从3835.22亿元增加到15677.77亿元，约增加4.08倍；全社会固定资产投资额从2501.86亿元增加到20112.35亿元，约增加8.04倍；招商引资额从326.28亿元增加到2368亿元，约增加7.3倍；外贸出口额从14.11亿美元增加到587.97亿美元，约增加41.68倍②。虽然武汉城市圈的县域经济体取得了很大的发展，但与长三角、珠三角城市圈县域经济体的发展相比仍然相对落后。由于第一产业是国民经济发展的重要基础，因此有必要对武汉城市圈36个县域经济体第一产业的发展效率进行分析，以便发现问题和寻求解决支持，进而推动武汉城市圈经济社会更快更好地可持续发展。

目前主流的对效率测算的研究方法有两种：数据包络研究法（Data Envelopment Analysis，简称DEA）和随机边界分析法（Stochastic Frontier Approach，也有学者翻译为随机前沿分析，简称SFA），这两者都是非参数估计方法，在实际中均得到了广泛的运用[1]。由于本文研究的主题是测算武汉城市圈县域经济体第一产业实际产出和理论最大产出的差距，故不适宜采用DEA方法[2]。传统的随机边界分析法暗含了一个重要的假定，即所有的生产个体的技术是同质的或无差异的。而在现实中，具体某个产业中的不同生产个体由于受不同的生产环境及其他诸多因素的影响，很难满足这个比较严格的假定，如果对所有的生产个体用一个相同的生产边界函数进行效率的估计与分析，容易造成有偏差的估计结果[3]。为克服这种局限，Mester（1996）[4]、Grifell（1997）[5]等采用简单的两步法进行处理，先依据生产个体的差异对样本进行分类，确保同类个体的技术是大致同质的，然后再不同类分别实施随机边界分析[6]。针对两步法的缺陷，Daniele Pacifico（2012）[7]提出了基于改进两步法的潜技术类别随机边界模型（Latent Class Stochastic Frontier Model，简称LCSFM），先依据可能影响类别的因素对生产个体进行潜分类，然后对不同潜技术类别实施随机边界分析[8]。本文采用LCSFM方法对武汉城市圈县域经济体第一产业发展的技术效率进行分析。

二、潜技术类别随机边界分析的理论模型

对技术效率进行随机边界分析的理论模型通常被设定为（下文以武汉城市圈县域经济体为例对模型的含义进行阐述）[9]：

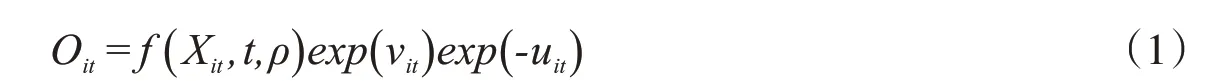
取自然对数转换后可以变化为：

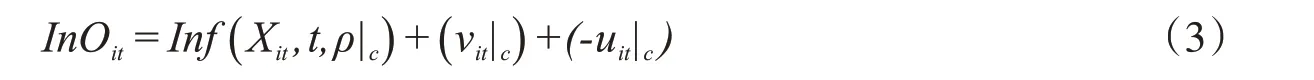
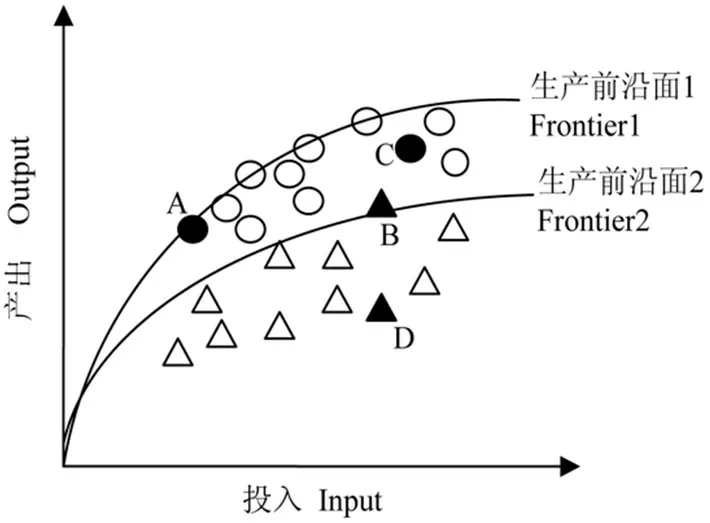
图1 LCSFM核心思想示意图③

在对生产个体进行分类的问题上，不同于早期使用直观指标进行分类的简单做法，Green（2005）[12]、Muthén（2003）[13]等提出了潜分类的办法，他们使用期望最大算法求解两个最大化问题后，便可算出每个生产个体归属于某个潜技术类别c的最大后验概率。目前使用Nlogit 和Mplus软件可以很方便求解每个生产个体所属的潜技术类别。

为详细地剖解产出的变动情况，在式（3）中对时间t进行全微分，可得：

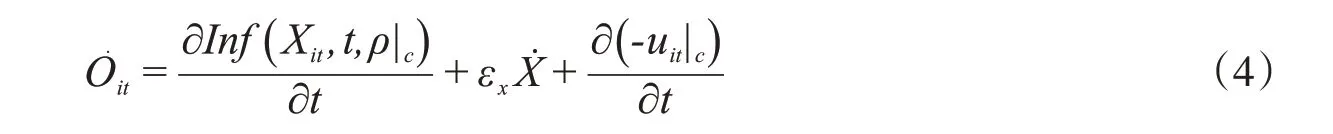
三、实证模型的建立

（一）变量说明、样本描述及实证模型的构建

本文数据来自于2010-2020年的《湖北统计年鉴》《中国农村统计年鉴》和《中国统计年鉴》，选取2009-2019年武汉城市圈36个县域经济体第一产业投入和产出的相关数据。

相关变量或指标说明如下：武汉城市圈县域经济体总产出O用36个县域经济体第一产业的生产总值衡量；生产要素资本投入指标K用各县域经济体投入全社会的固定资产额衡量；生产要素的劳动投入指标L用各县域经济体从事第一产业的人员数量衡量。在进行潜分类条件变量的选择上，借鉴Barro（1991）[14]、Mankiw（1992）[15]、赖永剑（2014）[16]和薛彩霞（2014）[17]的研究，并结合实际，将各县域经济体的开放程度KF和从事第一产业人员的经济实力SL作为区分潜技术类别的指标[18]。衡量县域经济体对外开放程度KF的相对指标构设为：（外贸出口额+实际利用外资额）/各县域经济体的地区生产总值；衡量从业人员经济实力SL的指标选定为第一产业人均纯收入。为剔除价格因素对研究的影响，本文以2005年为基期，对上述含有价格因素的指标进行相应的调整。表1分年度列出了武汉城市圈县域经济体第一产业发展的相关统计指标。

表1 变量的统计指标

表1 变量的统计指标（续）

（二）实证模型的构建

借鉴Barros（2008）的设定，本文构建如下超越对数形式的生产函数，作为实证的随机边界分析模型[19]：

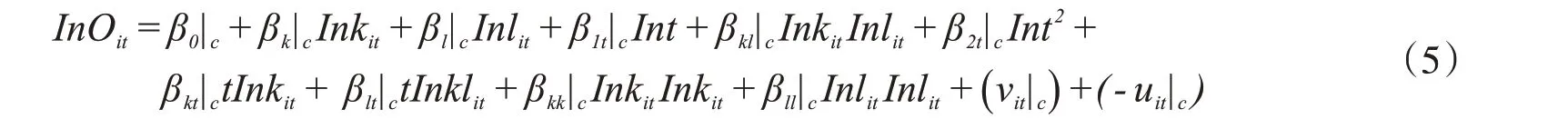
其中弹性εk、εl可以求解为：

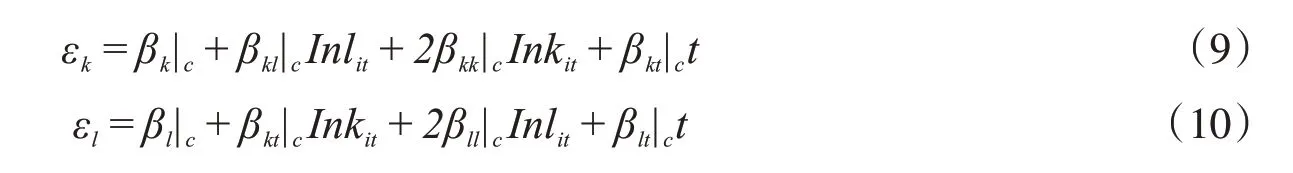
四、实证结果及分析

（一）武汉城市圈县域经济体潜技术类别数量的确定

潜技术类别的数量可以采用赤池信息准则（AIC）、贝叶斯信息准则（BIC）或调整后的贝叶斯信息准则（ABIC）进行筛选，AIC值、BIC和ABIC值最低的潜技术类别数量是最佳的[20]。根据两步法的要求，用Muthén开发的计量软件Mplus7.0估算了潜技术类别数量（前文设定的两个条件变量KF和SL），具体结果如表2。

表2 潜技术类别选择的相关统计值

从表2可知，当潜技术类别数量是2时，其AIC、BIC和ABIC的值均为最小，按照判定的准则，可知最优的潜技术类别应该为2个，当潜技术类别是3个时，Mplus7.0提示结果不可信，当潜技术类别数量是1时，三个判定值较大[21]。综合以上分析，武汉市城市圈县域经济体第一产业发展的潜技术类别最优数量为2。各县域的具体类别归属如下：（1）蔡甸区、江夏区、黄陂区、新洲区、汉南区、大冶市、华容区、鄂城区、孝南区、应城市、安陆市、汉川市、黄州区、云梦县、应城市、安陆市、汉川市、黄州区、武穴市、咸安区、嘉鱼县、赤壁市、仙桃市、潜江市和天门市归为一类，该类大多是大中城市的郊区县域和毗邻县域，整体经济实力发达（下文把这一类称为甲类县域）；（2）阳新县、梁子湖区、孝昌县、大悟县、团风县、红安县、罗田县、英山县、浠水县、蕲春县、黄梅县、麻城市、通城县、崇阳县、通山县归为一类，该类大多区位偏远，交通不便，经济实力较差（下文把这一类称为乙类县域）。这种分类的结果十分符合对这些县域的直观判断，也符合这些县域的实情。

（二）潜技术类别随机边界模型估计的结果及解释

根据上文构建的超越对数生产函数模型，结合潜技术类别分析的结论，得到表3的估计结果。

表3 重要参数的估计结果

为确保结论的准确性，还必须进行生产函数设定形式检验[22]。如果生产函数设定错误，那么就会影响到随机边界分析估计结论的有效性，因此将超越对数生产函数与Cobb-Douglas生产函数进行对比检验[23]。由于这两种生产函数既有联系又有区别，Cobb-Douglas 生产函数是超越对数生产函数所有二次项系数为0的极端情况，因此本文提出如下原假设进行检验，H0:βkl=β2t=βkt=βlt=βkk=βll=0 。如果不能拒绝原假设，就采用Cobb-Douglas生产函数；反之，表明所设定的函数形式是适合的（假设检验结果见表4）。

表4 假设检验

表4的检验结果表明，用Cobb-Douglas生产函数去研究武汉城市圈县域经济体第一产业发展的技术效率是不可行的，本文设定的函数形式是比较适合的。从表3可以看出，lnk（资本）的系数在甲乙两类县域均为正，且统计值显著，这说明资本的投入和武汉城市圈县域经济体第一产业的发展有着直接的关系，增加资本的投入能够达到推动第一产业发展的效果。lnl（劳动）的系数在甲类县域为正，统计值显著，这说明在甲类县域，劳动力的投入数量和第一产业的发展也有直接的关联，靠增加劳动力的投入数量对第一产业的产出有明显影响；lnl的系数在乙类县域为正，统计值显著（在1%的水平上），这表明在乙类县域，劳动力数量的投入能较大程度地推动该类县域第一产业的发展。t（时间变量）的系数在甲乙两类县域均为负，且在乙类县域较为显著（在5%的水平上），这表明随着时间的推移，技术效率有所降低。

资本和劳动交乘项lnk*lnl的系数在甲乙两类县域均为负，且统计值显著，这表明在甲乙两类县域资本和劳动均可能存在替代效应，且较为明显。时间和资本的交乘项t*lnk的系数在甲乙两类县域均为正，但统计值在乙类县域较为显著，则表明随着时间的推移，在甲乙两类县域资本的产出能力可能会逐步增强，但乙类县域更为明显。时间和劳动交乘项t*lnl的系数在甲乙两类县域均为正，且统计值显著，这表明随着时间的推移，在甲乙两类县域劳动的产出能力可能会明显地减弱。

时间非线性项t*t的系数在甲乙两类县域均为负，且统计值显著，这表明技术效率对推动甲乙两类县域第一产业的发展有着显著的负向影响，会明显降低产出。资本非线性项lnk*lnk的系数在甲乙两类县域均为负，统计值在甲类县域不显著，在乙类县域显著（在5%的水平上），这表明资本对推动甲类县域第一产业发展的正向非线性影响不明显，在乙类县域，这种正向的非线性影响更加不明显。劳动非线性项lnl*lnl的系数在甲乙两类县域均为正，统计值均不显著，则表明劳动对推动甲类县域第一产业的发展可能有着正向的非线性影响，对推动乙类县域第一产业的发展也可能有着正向的非线性影响，但均不明显。

（三）武汉城市圈县域经济体第一产业产出变动的分解及解释

为了更加直观地分清甲乙两类县域的差异，表5从技术进步变动、生产要素（资本、劳动）弹性变动等方面列出两类县域的差异性特征。

表5 甲乙两类县域技术进步和生产要素弹性变动差异

从表5可知，甲乙两类县域呈现明显的差异：甲类县域在技术进步变动和资本弹性变动两个方面均比乙类县域大，而在劳动弹性变动方面，乙类县域小于甲类县域。这说明与乙类县域相比较，技术进步和资本投入对甲类县域第一产业的产出有更强的影响，而劳动投入对两类县域第一产业的影响则相反。利用式（6）～（10），对武汉城市圈甲乙两类县域经济体第一产业的产出变动进行分解，分解的结果如表6。

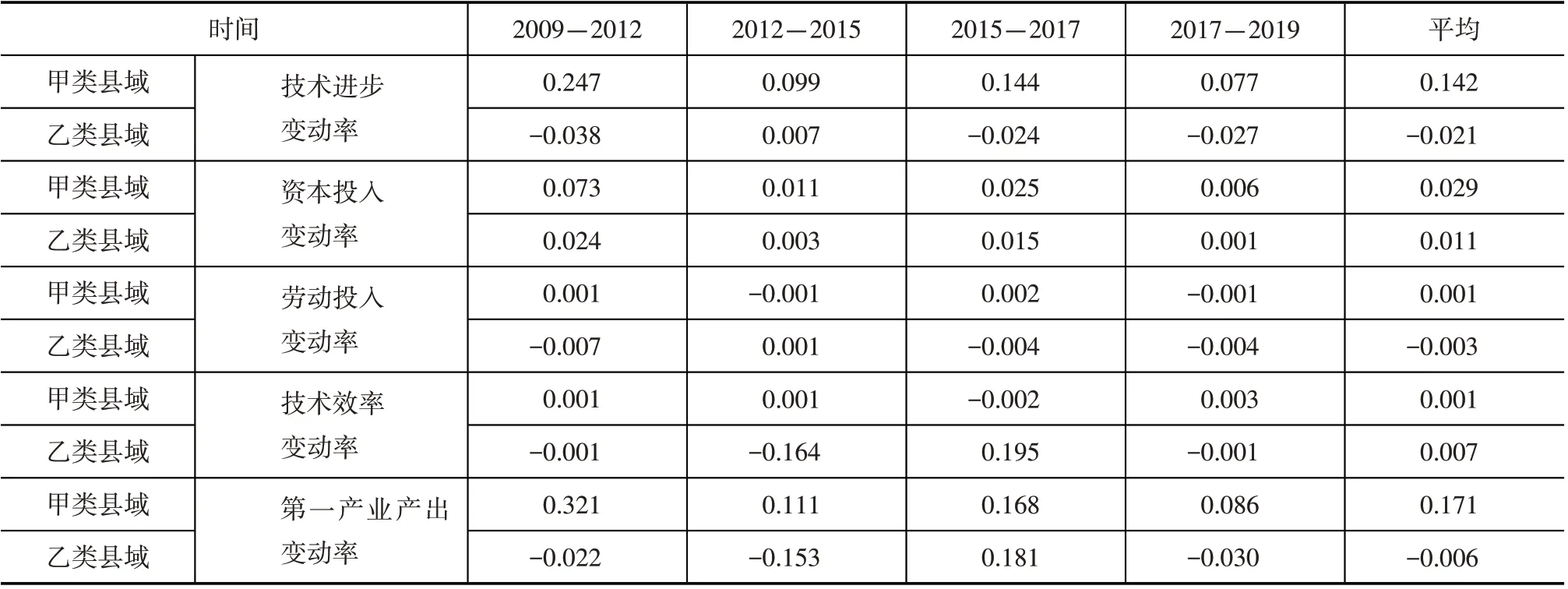
表6 甲乙两类县域第一产业产出变动率分解

从表6可知，在甲类县域第一产业产出的增长中，技术进步起了更重要的作用，究其原因，是因为甲类县域经济实力较强，而且绝大多数毗邻大中城市，容易引进先进的生产技术促进第一产业的发展，且先进的生产技术也容易得到广泛的使用；而乙类县域多属于老少边穷地区，交通不便，不容易引进先进生产技术，且不利于先进生产技术在该类县域使用。

从变化趋势来看，甲类县域的技术进步变动率有下降的趋势，而乙类县域的技术进步变动率却始终保持着较低水平的平稳，这主要是由于甲类县域经济发展的重心不在第一产业，随着时间的推移，原有技术进步对第一产业的边际推动越来越小，而乙类县域由于地理、交通等区位环境方面的限制，技术进步对该类县域第一产业的推动始终在低水平上徘徊。

在生产要素投入的变动率方面，甲类县域的资本投入变动率高于乙类县域，这主要是因为甲类县域比乙类县域经济实力雄厚，能投入更多的资本驱动第一产业的发展。和资本投入变动率相比，甲类县域和乙类县域的劳动投入变动率都很低，这表明两类县域驱动第一产业发展更多是靠资本驱动，第一产业的发展方式逐步走向集约化，传统的粗放化发展有所改变，特别对乙类县域来说，平均劳动投入变动率甚至为负数，这表明在相对贫困乙类县域有一部分第一产业从业人员转向了其他产业。

在技术效率变动率方面，甲乙两类县域的技术效率变动率均不大，基本不随时间的变化。这说明技术效率变动在推动甲乙两类县域第一产业发展过程中发挥作用有限。

五、结论和建议

本文利用武汉城市圈36个县域经济体2009-2019年第一产业发展的面板数据，基于改进的两步法建立了超越对数形式的潜技术类别随机边界模型，在考虑县域经济体异质性的基础上对上述县域第一产业发展的技术效率进行分析，得出以下结论：

由于对外开放程度和第一产业从业人员经济实力的不同，武汉城市圈36个县域经济体第一产业的发展不是同质的，如果不考虑它们之间的异质性直接分析，容易导致估计结果的偏误。用上述两个条件变量进行潜分类，可以把这36个县域经济体第一产业的发展分成甲乙两种类型，它们有不同的随机边界，存在很大的差异。

甲类县域在技术进步变动和资本弹性变动两个方面均比乙类县域大，而在劳动弹性变动方面，乙类县域小于甲类县域。这说明与乙类县域相比较，甲类县域距离自身的随机边界更近，技术进步和资本投入对该类县域第一产业的产出有更强的影响，而劳动投入对两类县域第一产业的影响则相反。

从变化趋势来看，甲类县域的技术进步变动率有下降的趋势，而乙类县域的技术进步变动率却始终保持着较低水平的平稳。

在生产要素投入的变动率方面，甲类县域的资本投入变动率高于乙类县域；甲乙两类县域的劳动投入变动率都很低，这表明两类县域驱动第一产业发展更多是靠资本驱动，第一产业的发展方式逐步走向集约化，传统的粗放化发展有所改变；在技术效率变动率方面，技术效率的变动在推动两类县域第一产业发展过程中，基本没有发挥太多作用。

根据以上分析，为推动武汉城市圈县域经济体第一产业的发展，政府应该针对不同的县域因地制宜采取发展措施。在甲类县域，应侧重于技术和资本的投入，提高生产技术和资本投入的利用效率；在乙类县域，可以在第一产业的发展过程中适当增大劳动力的投入，如加大对劳动力农业科技知识和实用技术的培训等，提升劳动力的技能素质。

注 释：

①武汉城市圈的县域经济体有36个，其中武汉市有5个（蔡甸区、江夏区、黄陂区、新洲区和汉南区）；黄石市有2个（阳新县、大冶市）；鄂州市有3个（梁子湖区、华容区和鄂城区）；孝感市有7个（孝南区、孝昌县、应城市、安陆市、汉川市、大悟县和云梦县）；黄冈市有10个（黄州区、麻城市、武穴市、团风县、红安县、罗田县、英山县、浠水县、蕲春县和黄梅县）；咸宁市有6个（咸安区、赤壁市、嘉鱼县、通城县、崇阳县、通山县）；省直管市有3个（仙桃市、潜江市和天门市）。

②资料来源于湖北省统计局公布的2009 年至2019 年各年度《湖北省统计年鉴》，具体网站地址为：http://tjj.hubei.gov.cn/tjsj/sjkscx/tjnj/qstjnj/。

③资料来源于参考文献[3]。图中的○表示适用于生产前沿面1的县域经济个体；△表示适用于生产前沿面2的县域经济体个体；县域经济体A和县域经济体B处在各自的生产前沿面上，技术效率完全有效；县域经济体C和县域经济体D处在各自生产前沿面的下方，技术效率非完全有效。因为不同的县域经济体个体归属不同的类别，如果用传统的SFA方法，就会导致研究结论的偏误。