耗散性非自治电路的确定与不定解

黄炳华 陈新苗 韦善革

耗散性非自治电路的确定与不定解

黄炳华 陈新苗 韦善革

（广西大学电气工程学院，南宁 530004）

谐波平衡原理只能求非线性动态系统进入稳态的振荡解，无法求出起始暂态过程，由于没有引入初始条件，它无法求出自振荡分量的初始相角。关于谐波分析法，如果最初谐波项的假设能够符合被求电路的物理实际，会得到有实数解的正确结果。反之实数解的缺失，说明初始假设不合理。为此必须重新设定谐波的形式。二阶非自治电路含有自激和受迫两个谐波分量，是一个耦合振荡。本文论述五次方项的非自治电路，用等效基波电导替代非线性阻尼，可将简化的网络划分成为两个分部，各分部有各自单独的振荡频率，可以单独列出微分方程而后联合求解。分部网络的功率各自独立维持平衡，是求解非自治电路的有效方法，有广泛的普遍性和适用性。

谐波分析；非自治电路；非线性振荡；耦合；初相位

0 引言

对于非自治电路，如果也采用谐波分析法求解，现有许多国内外文献的论述，对于最初谐波项的预设，并没有包含一个频率独立的自振谐波项。尽管存在多种多样的近似解析法[8-10]，都不具有适用一般情况的普遍性，大都是针对某些常见的具体方程提出一些近似的解析法，例如采用摄动法（perturbation method）或小参数的缓变方法等。传统谐波分析法存在一定局限性，Mickens R. E.已经做出有关评论[11]。近年来的文献提出将谐波分析法建立在功率平衡理论的基础上，对于包含多谐波成分的电路网络，每一谐波成分要各自独自遵守复功率平衡，即频域的功率平衡定理；并提出应该恰当地预设谐波项的最佳形式，从而使谐波平衡原理能够获得进一步的合理推广应用[12-15]。非自治振荡电路包含自激和受迫两个主要谐波成分的混频，主谐波解并不是两个成分的叠加，而是两者的非线性耦合[16-19]。

一般地，给出微分方程必须包含给出起始条件，题设不包含起始条件的微分方程是不完整的，对于耗散型含阻尼项的非自治电路，根据微分方程的内在本质特征，在没有起始条件的情况下，留下方程解的不定部分暂且不解，只求方程可解的确定部分，简化地求出进入稳态振荡的基本主要部分称为主谐波平衡原理，简化解的初相位是不定的，这种解法适用于一般非自治电路。

本文还探讨非自治电路中，自振荡成分是否一定存在。电路中并不存在有自振频率的电源，自振谐波是由于电路中包含非线性变频或负阻引起的振荡成分，它存在的条件是遵守频域功率平衡定理的两个方面：①两个振荡成分存在相互影响的非线性耦合关系，可以依靠非线性变频或负阻获得功率来源；②各谐波成分各自维持自身复功率平衡，各个谐波成分的功率盈亏不能互相填补。电力系统中出现有害寄生谐波的原因与电路中存在各种非线性变频或整流换流设备密切相关。谐波的出现严重危害电力系统的稳定安全经济运行。为了保证电能供应质量、改善系统运行的经济性能、消灭谐波污染引起的能量损失、抑制寄生谐波的出现，破坏谐波的功率平衡是一种有效的方法[20-22]。反之，为了改善电气设备的运行性能，也可以利用三次谐波的注入，使电机稳态性能的优化效果达到最佳[23]；或利用多谐波并存能够共同产生更大的机械功率来改善电机的起动性能[24]。以上从正反两方面说明，谐波的存在与维持该谐波成分的功率平衡密切相关。

1 自治电路的不定解

1.1 含三次方特性的自治电路

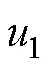
图1 范德堡电路

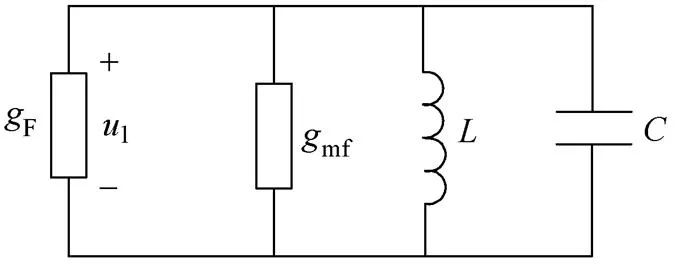
图2 基波电路

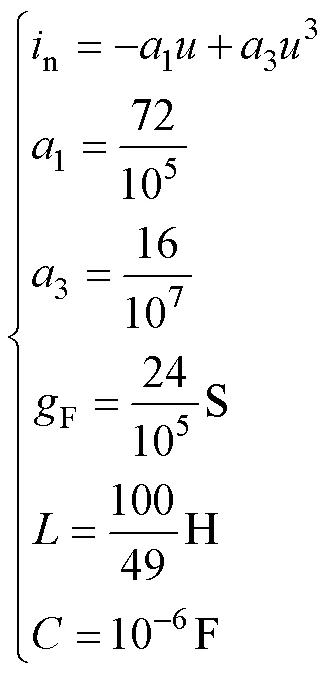
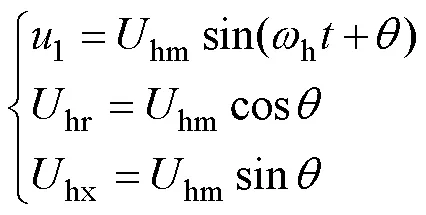
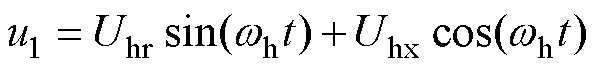
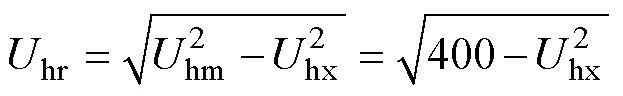
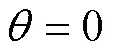
1.2 方程的本质特征

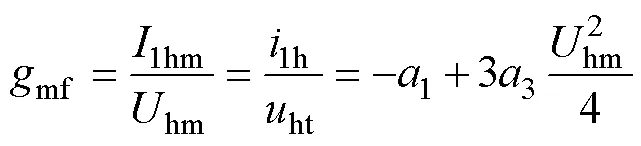
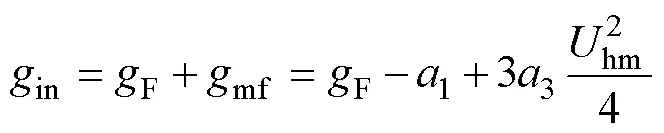
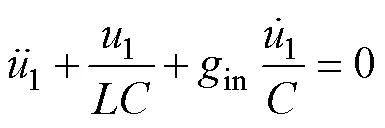
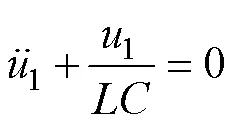
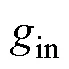
1.3 含五次方特性的自治电路

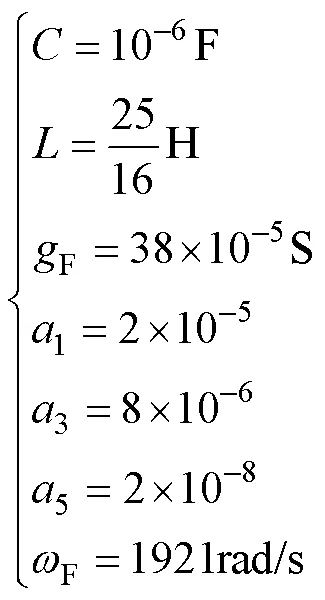
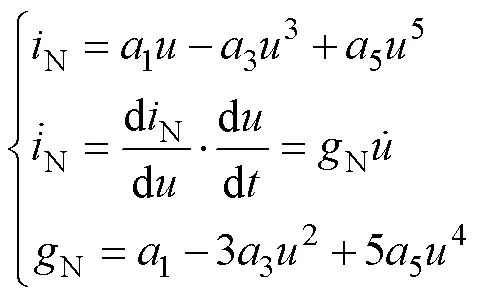
（13）

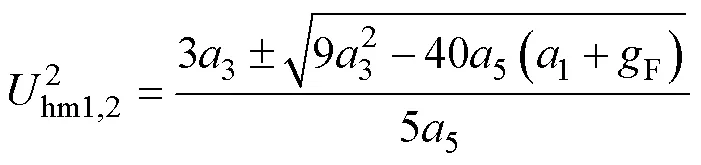
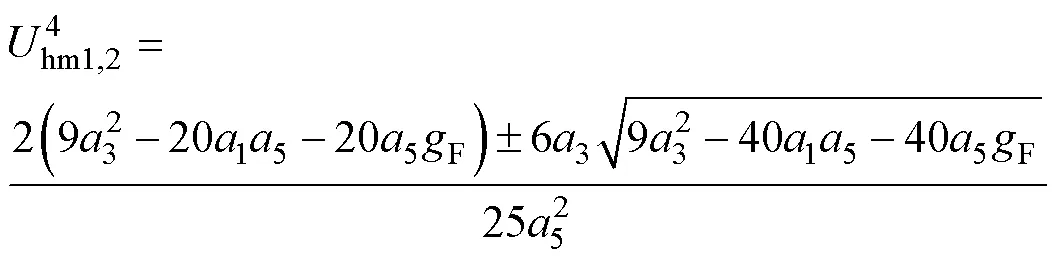
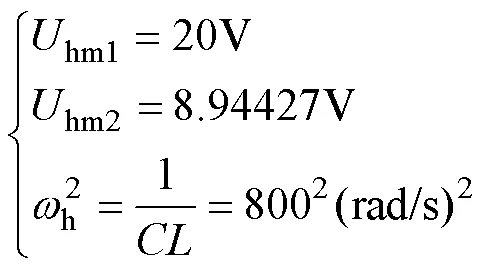
2 含三次方特性的非自治电路

2.1 用传统的谐波平衡法求解

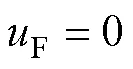
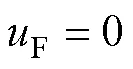
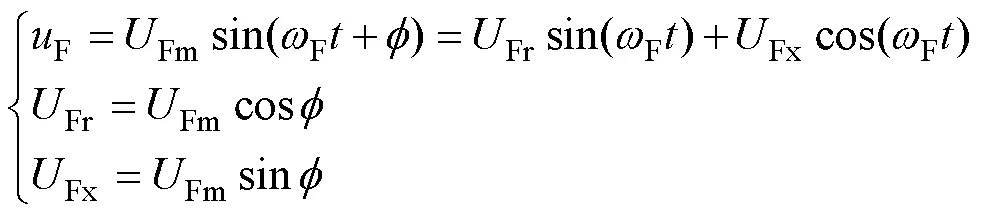
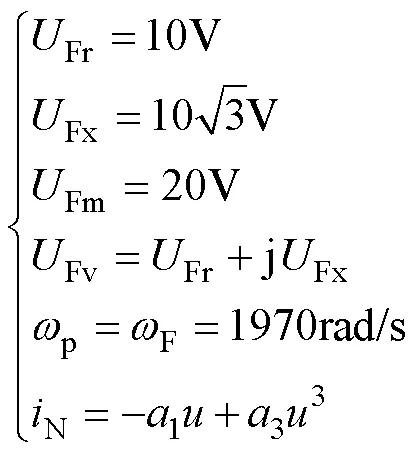
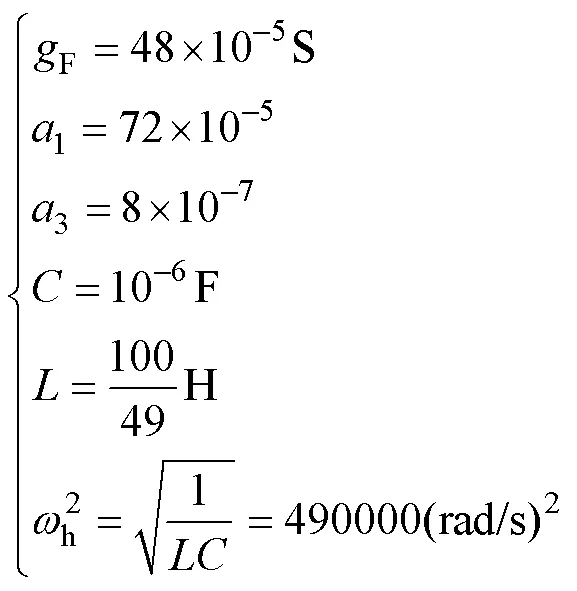
互耦合的主谐波分量，将电路划分成两个分部网络如图6和图7所示，两分部网络各支路电压电流可

图6 自振分部网络

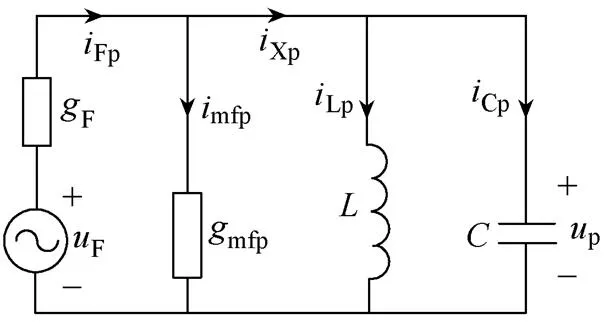
图7 受迫分部网络

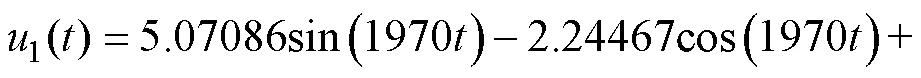
表1 当时，式（21）的主谐波解

注：SOE为self-oscillation existence，SOD为self-oscillation disappearance。

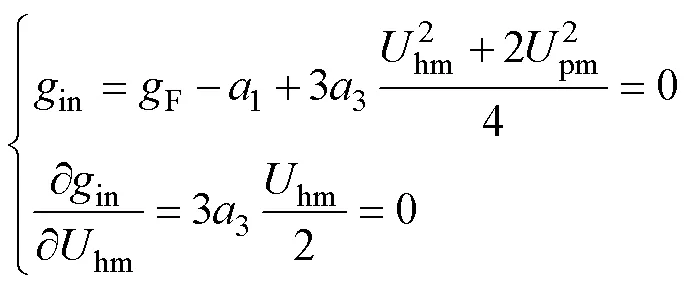
2.2 分部网络用零阻尼力求方程的稳态振荡解

电路图5微分方程式（21）包含两个主谐波分量，各谐波分量要各自遵守各种电路定律。在考虑两主谐波分量间非线性耦合的定量关系后，可将网络按两个频率划分成两个分部网络如图6和图7所

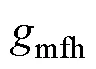
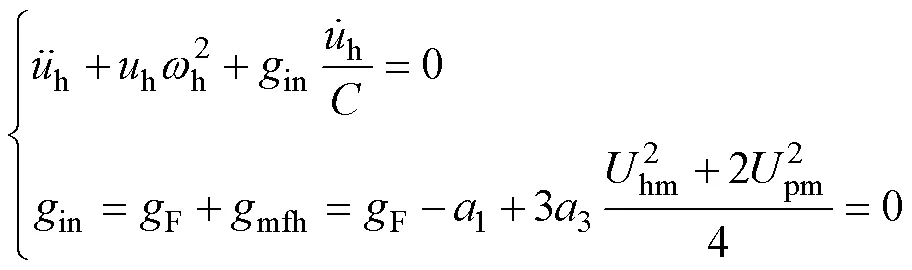
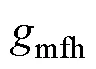
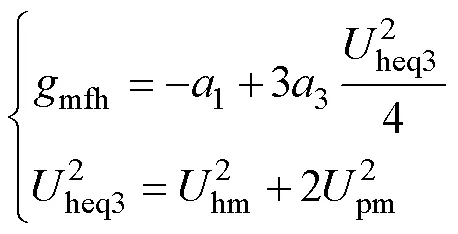
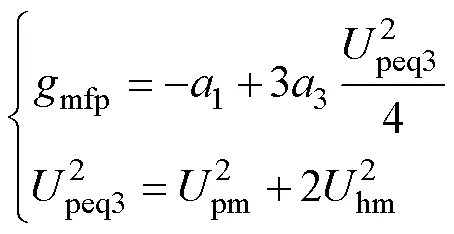
以下说明三次方特性的非自治电路，如何由式（28）和式（29）求两个微分方程所构成的主谐 波解。

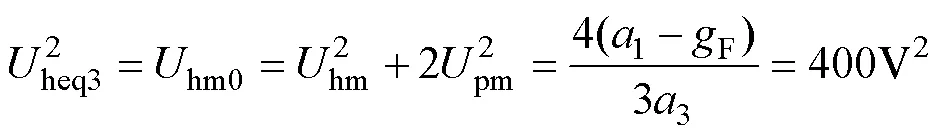
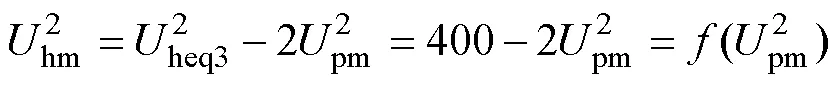
得出

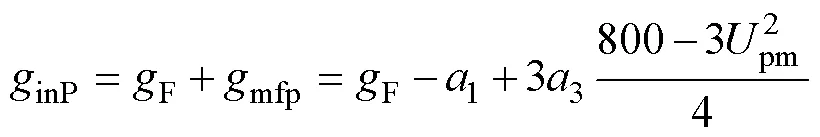
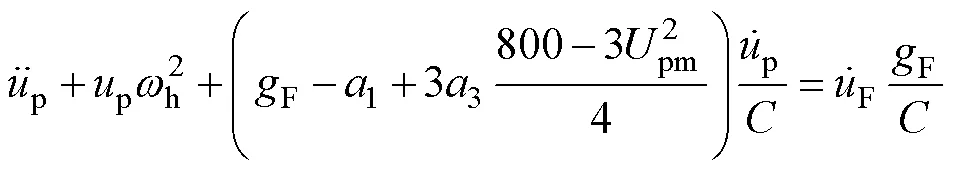
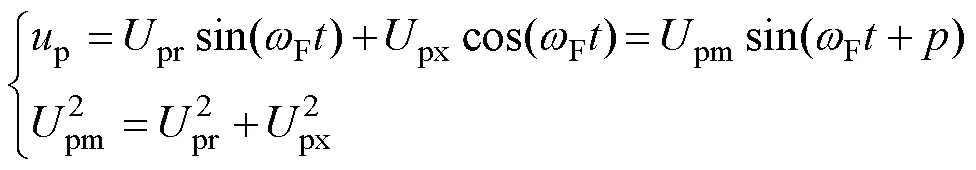
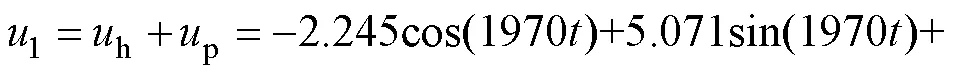
2.3 分部网络用相量方程求主谐波解

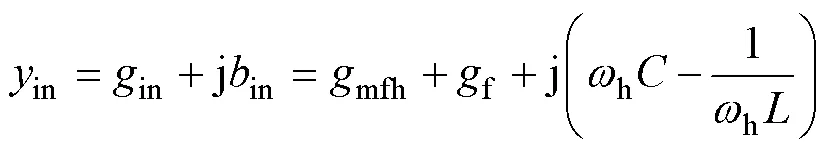
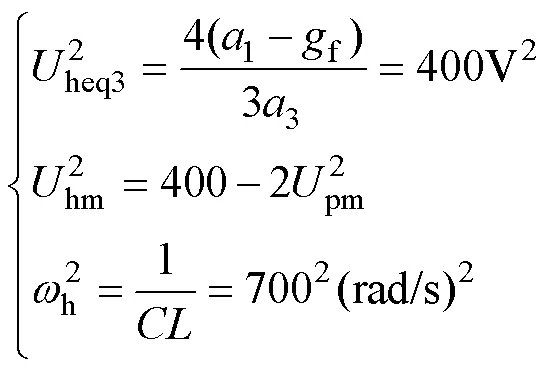
两分部网络可各自用相量方程求解，但两个分部的背景参照频率不同，因而两个主谐波的相量值

3 含五次方特性的非自治电路

3.1 用传统谐波平衡原理求解非自治电路

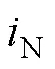
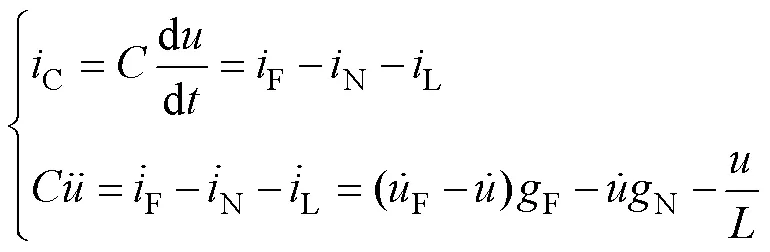
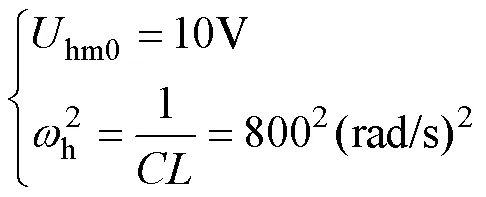
谐波平衡原理如果按式（23）预设自振分量的形式，非常不利于求解，会使MATH程序无法求解。如果按式（24）预设定，并且式中的不作为求解变量，只作为一个未给出数值的待定量留在程序中，并不影响求出自振幅值hm，也不影响分析自振分量是否存在。MATH程序NB7-table2.nb按式（24）预设定，得到更加合理的结果，它用hm=0显示自振消失。程序求出的主谐波解见表2。

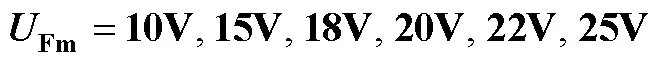
表2 当时，式（50）的主谐波解

由表2数据可得出：①表2第一行可发现其中列入10a、10b和10c三种数据，说明五次方特性的

3.2 分部网络用零阻尼求稳态振荡解

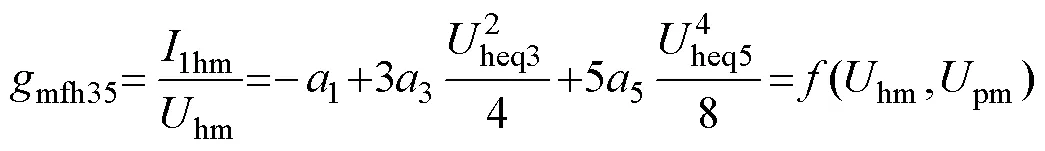
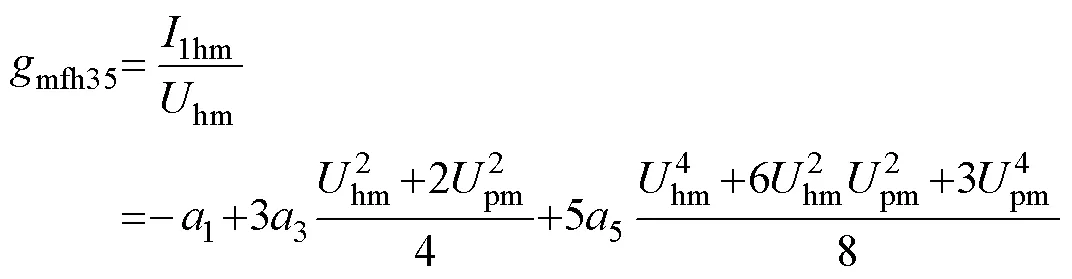
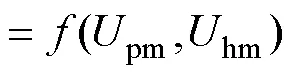
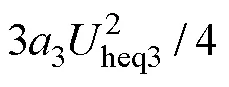
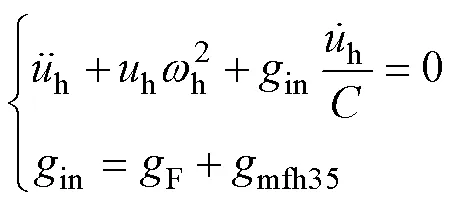
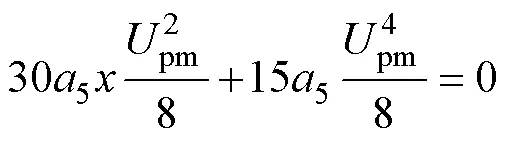
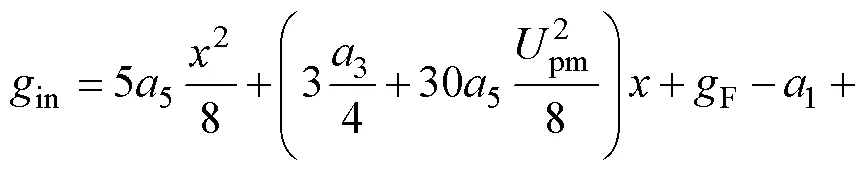
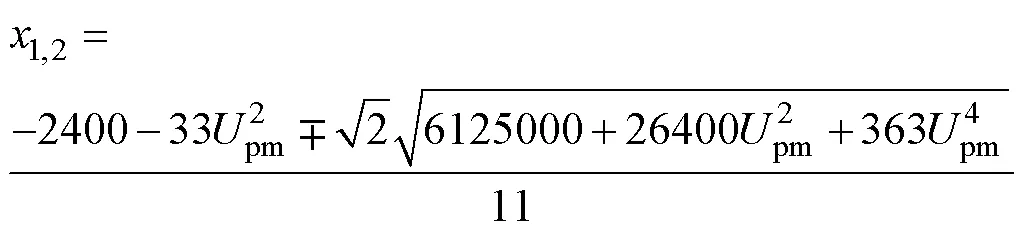
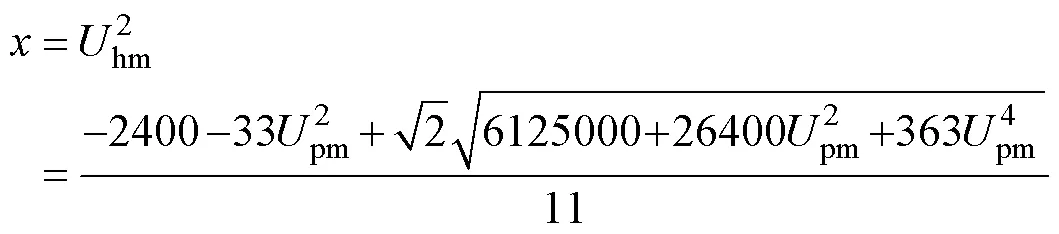
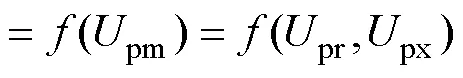
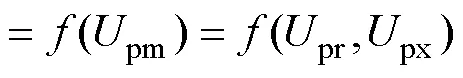
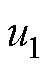
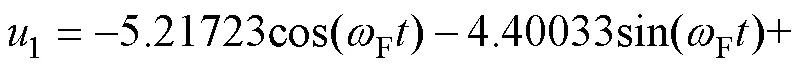
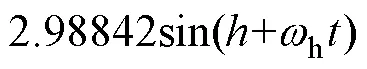
4 主谐波平衡方程的一般表达式

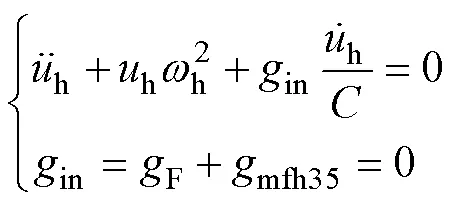
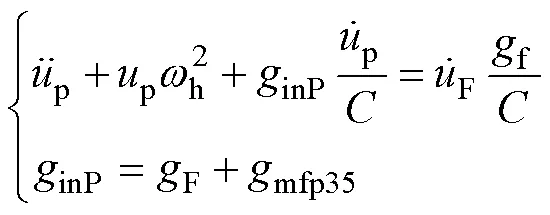
5 复功率平衡验证与自振消失的临界值

5.1 自振分部网络的复功率平衡验证

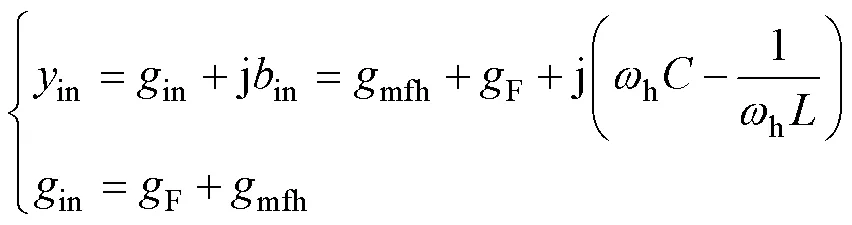
5.2 受迫分部网络的复功率平衡验证

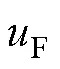
程序NB7-table-uFm15、uFm18-powerbalance对此做了成功可靠的验证。

5.3 自振荡消失的最低受迫分量称为临界电压

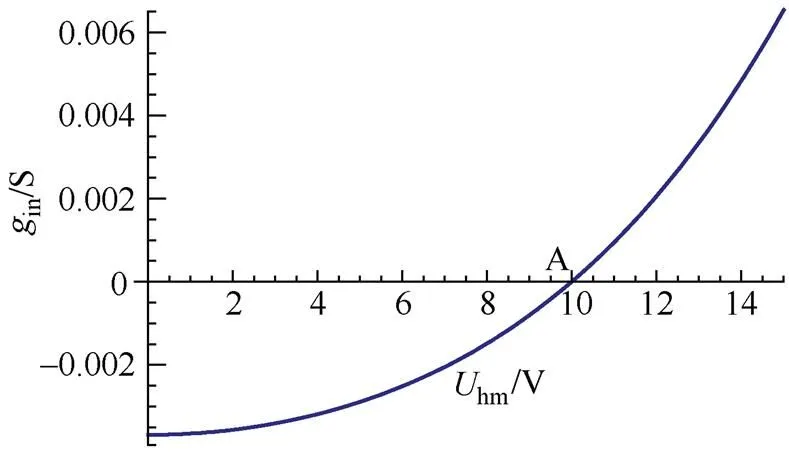
图8 ，曲线

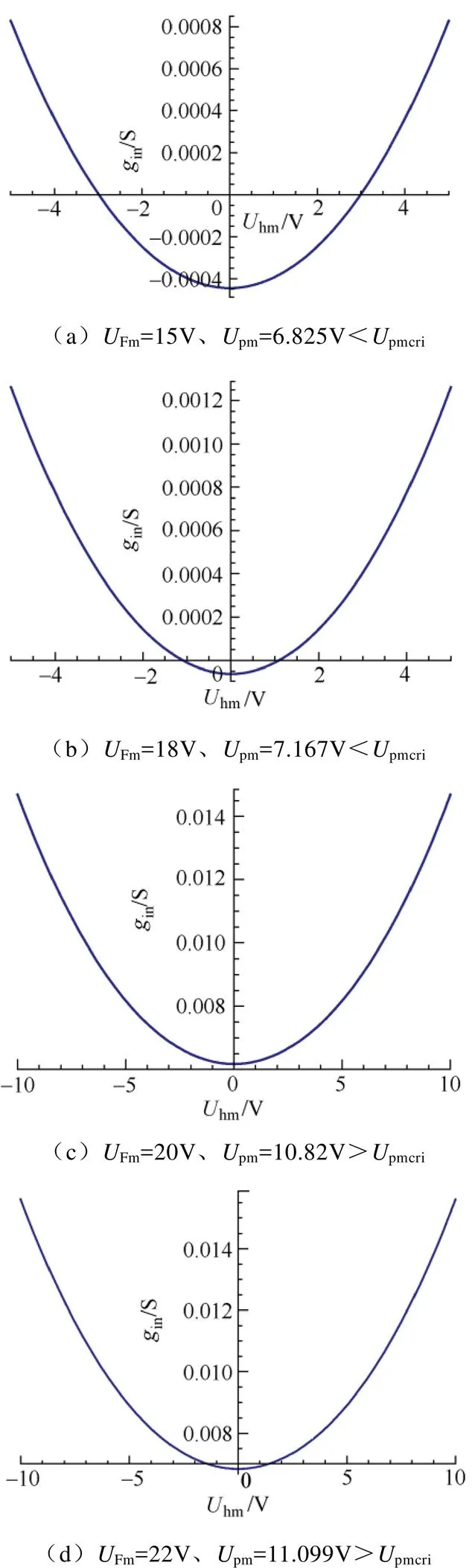
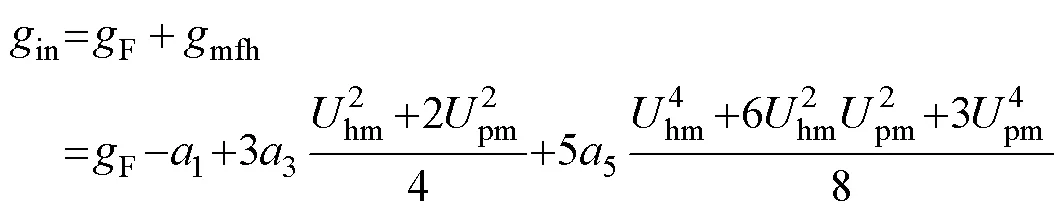
（70）

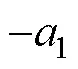
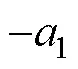
次谐波的功率平衡。

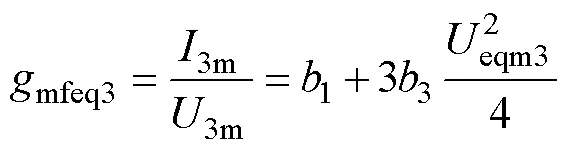
6 结论

可解的，仍然可以用线性微分方程理论求出两个主谐波的耦合解。本文采用传统谐波分析法、零阻尼法、相量方程求解法三种方法最后得出数据完全一致的结论。

附录 MATH程序压缩夹

（1）NB1-indef.nb；包括NB1-no-ang.nb NB1-have- ang.nb NB1-uhr+uhx.nb

（2）NB2-exam2-First.nb;

（3）NB3-0-exam3-First.nb; NB3-table1.nb;

（4）NB4-critical.nb;

（5）NB5-damping.nb;

（6）NB6-phesor.nb;

（7）NB7-0-exam4-First.nb; NB7-table2.nb;

（8）NB8-equivalent.nb;

（9）NB9-damping2.nb;

（10）NB10-Critical2.nb;

（11）NB11-peq13.nb

[1] 黄炳华, 钮利荣, 蔺兰峰, 等. 功率平衡基础上的基波分析法[J]. 电子学报, 2007, 35(10): 1994-1998.

[2] 黄炳华, 黄新民, 韦善革. 用基波平衡原理分析非线性振荡与混沌[J]. 通信学报, 2008, 29(1): 65-70.

[3] 黄炳华, 黄新民, 李世作. 功率平衡与基波分析法[J]. 电路与系统学报, 2003, 8(1): 72-76.

[4] 黄炳华, 黄新民, 张驰. 电子网络振荡与稳定的基波分析法[J]. 电子科技大学学报, 2006, 35(1): 47-50.

[5] 黄炳华, 宋春宁, 黄洪全. 非线性电子网络的基波分析法[J]. 固体电子学研究与进展, 2003, 23(1): 35-41.

[6] 黄炳华, 黄新民, 张海明, 等. 各类自激振荡的基波分析法[J]. 固体电子学研究与进展, 2005, 25(1): 102-107.

[7] 黄炳华, 黄新民, 王庆华. 用基波平衡原理分析非线性电子网络的稳定性[J]. 固体电子学研究与进展, 2006, 26(1): 43-48.

[8] 肖达川. 线性与非线性电路[M]. 修订版. 北京: 科学出版社, 1992.

[9] 褚亦清, 李翠英. 非线性振动分析[M]. 北京: 北京理工大学出版社, 1996.

[10] 高金峰. 非线性电路与混沌[M]. 北京: 科学出版社, 2005.

[11] MICKENS R E. Comments on the method of harmonic balance[J]. Journal of Sound Vibration, 1984, 94(3): 456-460.

[12] HUANG Binghua, YANG Guangsong, WEI Yafen, et al. Harmonic analysis method based on power balance[J]. Applied Mechanics and Materials, 2013, 325-326: 1508-1514.

[13] HUANG Binghua, LI Guangming, LIN Huijie. Power balance theorem of frequency domain and its appli- cation[J]. Journal of Modern Physics, 2014, 5(12): 1097-1108.

[14] 王庆华, 黄炳华. 混频振荡与功率平衡的研究[J]. 现代电子技术, 2018, 41(21): 173-178.

[15] HUANG Binghua, HUANG Xinmin, LI Hui. Main components of harmonic solutions of nonlinear oscillations[J]. Procedia Engineering, 2011, 16: 325- 332.

[16] 黄炳华, 周珊, 林晓东. 非自治振荡电路的功率平衡[J]. 固体电子学研究与进展, 2018, 38(5): 333-342.

[17] 黄炳华, 黄昌琴, 蔡义明. 非自治振荡电路的主谐波分析法[J]. 电子学报, 2019, 47(9): 2003-2011.

[18] 黄炳华, 周珊. 非线性解的多种成份及其特征[J]. 固体电子学研究与进展, 2019, 39(6): 436-443.

[19] 黄炳华, 周珊, 黄昌琴. 用相图描写混频电路[J]. 固体电子学研究与进展, 2019, 39(5): 364-370.

[20] 严静, 邵振国. 电能质量谐波监测与评估综述[J]. 电气技术, 2020, 21(7): 1-7.

[21] 陈和洋, 吴文宣, 郑文迪, 等. 电力系统谐波检测方法综述[J]. 电气技术, 2019, 20(9): 1-6.

[22] 孙佳伟. 一种谐波自消除整流器的特性研究[J]. 电气技术, 2020, 21(3): 52-58.

[23] 孟繁庆, 易新强, 刘海涛, 等. 三次谐波注入下多相感应电机稳态性能分析[J]. 电工技术学报, 2020, 35(16): 3396-3405.

[24] 阚超豪, 鲍习昌, 金科, 等. 绕线转子无刷双馈电机多谐波联合起动过程中磁动势及性能分析[J]. 电工技术学报, 2020, 35(3): 481-493.

The definite and indefinite-solutions in the dissipative non-autonomous circuits

HUANG Binghua CHEN Xinmiao WEI Shan’ge

(School of Electrical Engineering, Guangxi University, Nanning 530004)

The harmonic balance principle can only seek the stable oscillation solution of non-linear dynamic system, but it cannot solve the initial transient process. Since the initial condition is not introduced, the initial phase angle of the self-excited oscillation component cannot be obtained. Concerning harmonic analysis method, if the initial assumption of the harmonic components fits the physical characteristics of the circuit, the correct real number solution will be obtained. By contrast, the absence of real number solution implies an improper initial assumption. In this case, to reset the form of harmonic components is necessary. Containing both self-excited and forced oscillation components, the second order non-autonomous circuit is a coupled oscillation. The non-autonomous circuits of fifth power are discussed in this paper. The non-linear damping factor can be replaced by equivalent first wave conduction. The simplification network can be divided into two subsections, each of which possess independent oscillation frequency. The differential equation can independently be described and then be solved together. The power balance of each subsection network must be maintained. It is an effective way to solve non-autonomous circuits. It possesses widely universality and applicability.

harmonic analysis; non-autonomous circuits; nonlinear oscillation; coupling; initial phase angle

2021-12-29

2022-07-06

黄炳华（1940—），男，福建省厦门市人，教授，主要研究方向为非线性电路含多谐波成分的功率计算，用功率平衡理论研究非线性振荡，用主谐波平衡原理研究非自治电路的主谐波解。

国家自然科学基金（60662001）非线性微分方程基础上的功率平衡