石墨尾矿砂混凝土梁抗弯性能试验研究

冯博雅， 夏洪春,2， 朱训国,2， 刘晓洲

(1.大连大学 建筑工程学院， 辽宁 大连 116622； 2.大连大学 复杂结构系统灾害预测与防治重点实验室，辽宁 大连 116622； 3.衢州学院 建筑工程学院， 浙江 衢州 324000)

石墨尾矿砂是选矿厂生产石墨后排放的矿业废渣，传统处理方法为露天矿区堆放。根据国土资源部中国矿产资源报告[1]，截至2019年，我国石墨生产量达9 216.5万t，较2018年增长了67.7%，而每生产1t石墨，就会产生10t尾矿。一方面，石墨尾矿长期堆积会对其周边的空气、地表水、地下水等造成严重污染；另一方面，随着我国建筑业的高速发展，对天然砂的需求日益增长，而天然砂作为不可再生资源已濒临枯竭，国家已明令禁止再开采。鉴于此，如果能利用与天然砂物性相似，经浮选后的石墨尾矿砂部分替代天然砂，配制混凝土并应用于工程建设中，不仅符合国家对建材固废再利用的总体规划，而且还能够达到治理环境、节约资源的双重目的。

近年来，刘洪波、李犇[2-6]等对石墨尾矿水泥基材料及混凝土材料进行了研究，结果表明，与普通混凝土相比，一定掺量的石墨尾矿混凝土其抗压强度、压敏特性及抗渗性能表现更优，且加入石墨尾矿砂有利于提升水泥基材料的力学性能。王亮量等[7]研究了石墨尾矿混凝土的导电性和力学性能之间的关系，并确立了电阻率和抗压强度间的最优方程。孙小巍等[8]通过试验方法，研究了高泡沫混凝土的抗压性能，结果表明，掺入适量的石墨尾矿砂可以明显提升其抗压强度。目前，关于混凝土梁的抗弯试验以及极限承载力和挠度计算的相关研究已经取得了丰硕的成果[9-14],而在不同细骨料砂的替代及其钢筋混凝土梁的力学性能方面也有大量学者进行了研究。李志强等[15]对沙漠砂混凝土梁进行了抗弯性能研究，结果表明，沙漠砂混凝土梁的破坏形态及破坏机理与普通混凝土梁基本相同，可以应用于工程实际。周梅[16]、王庆贺[17]等学者对自然煤矸砂混凝土梁进行了抗弯性能研究，结果表明，单掺100%自燃煤矸石细骨料时，开裂弯矩与极限弯矩分别提高5.44%和2.00%。

目前，关于石墨尾矿砂混凝土的研究主要集中在材料性能方面，而针对石墨尾矿砂混凝土梁的抗弯性能试验研究则鲜见报道。因此，本试验利用石墨尾矿砂替代部分天然砂制备混凝土梁，在相同试验条件下，对不同石墨尾矿砂取代率(0、10%、20%、30%、40%)的混凝土梁进行三分点加载试验，通过分析其破坏形态、裂缝发展过程以及试验梁的荷载-挠度规律，探究不同取代率的混凝土梁的极限弯矩，并提出适用于石墨尾矿砂混凝土梁的极限承载力计算公式，以期为石墨尾矿砂混凝土构件应用于工程实际提供参考依据。

1 试验概况

1.1 原材料

1) 水泥：选用大连富民水泥制造公司生产的P.O42.5普通硅酸盐水泥。

2) 石子：选用大连瓦房店砂石厂生产的碎石，粒径为5～20mm，级配良好，表观密度为2 650 kg/m3。

3) 天然河砂：选用大连瓦房店砂石厂生产的河砂，细度模数为2.49。

4) 石墨尾矿砂：采用黑龙江省鸡西市石墨尾矿砂库的石墨尾矿砂。天然砂与石墨尾矿砂的物理特征详见表1。其中pH值测定方法为：称100 g砂子样品，溶解于100 mL纯水中，静置30 min后，用滤纸过滤，然后测定溶液的pH值。

5) 聚羧酸减水剂：选用大连市铭源科技开发有限公司生产的MZ-10C聚羧酸高性能减水剂。由表1可知，石墨尾矿砂的吸水率较天然砂高，本试验加入聚羧酸减水剂，用以增加混凝土的和易性。

表1 石墨尾矿砂与天然砂的物理性质

6) 钢筋：梁构件的受拉纵筋采用直径为10 mm的HRB400钢筋，对其取样进行材性试验，测得屈服强度为415 MPa。

1.2 配合比设计

根据配合比，制备了石墨尾矿砂取代率为0、10%、20%、30%、40%的石墨尾矿砂混凝土，通过对预留的养护28 d的100 mm×100 mm×100 mm的立方体试块进行试验，测量石墨尾矿砂混凝土的立方体抗压强度fcu，其配合比和力学性能如表2所示。需要说明的是，表中砂率为30%，与工程中通用的泵送混凝土相比明显偏低，这是因为砂的细度模数较小时，砂中颗粒多，混凝土的黏聚性较易得到保证，故采用较小的砂率，且本试验为非泵送混凝土，而泵送混凝土的砂率比非泵送混凝土的砂率要高2%～5%，故本试验采用的砂率比工程中的泵送混凝土低。

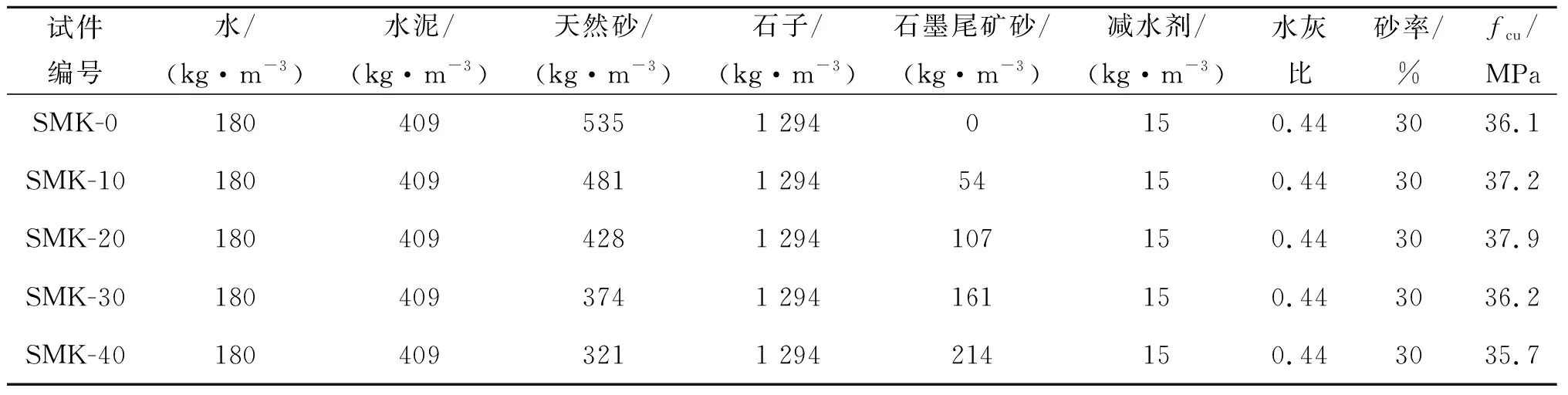
表2 1 m3石墨尾矿砂混凝土配合比及力学性能

1.3 试验梁设计

本试验制作的梁尺寸均为：长度1 600 mm，截面尺寸120 mm×180 mm，净跨1 500 mm。其中一根梁为天然砂混凝土梁(对比梁)，其余四根为石墨尾矿砂混凝土梁，取代率分别为10%、20%、30%、40%，试件制作见图1。为研究石墨尾矿砂混凝土梁的抗弯性能，所有试验梁均采用相同配筋率，纵向受拉钢筋的配筋率为1.257%，纵筋保护层厚度为20 mm，梁的尺寸及配筋详见图2。

图1 试件制作过程图 Fig.1 Production process of the test piece

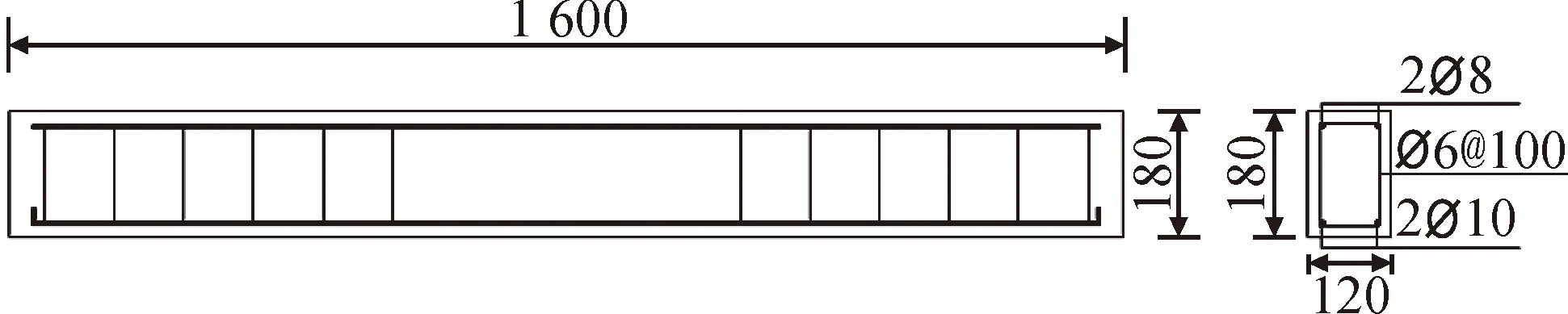
图2 梁的尺寸及配筋图(单位：mm)Fig.2 Beam size and reinforcement diagram(unit: mm)

1.4 试验装置及测量内容

试验采用三分点加载方式，在跨中形成500mm纯弯段，加载装置和测点布置见图3。按照《混凝土结构试验方法标准》(GB/T 50152—2012)[18]对混凝土梁进行抗弯试验，用液压机施加集中荷载，压力传感器置于分配梁跨中以实现两集中力三分点加载方式，试验加载前对试验梁进行预加载，以确保仪器的正常工作以及各点位的接触正常。开始时，加载方式按每级3kN加载，每次加载持续3 min，然后观察梁表面裂缝变化，当试件出现第一条裂缝后，以每级5kN为级差加载，随着荷载的逐渐加大，裂缝数量逐渐增多，裂缝不断向上延伸且裂缝宽度增大，用笔标出试验梁出现的裂缝，并记录受力荷载以及裂缝宽度。

图3 测点布置和加载装置图Fig.3 Layout of measuring points and loading device diagram

试验主要测量内容：①试验梁开裂荷载、极限荷载以及裂缝发展过程，裂缝发展过程用裂缝测宽仪观测；②应变，在梁跨中沿梁高均匀布置5个混凝土应变片测量混凝土应变；③荷载-挠度变化。

2 试验结果及分析

2.1 试验破坏现象

通过观察试验梁的弯曲加载试验，发现石墨尾矿砂混凝土梁的破坏过程、裂缝发展过程与普通混凝土梁基本一致，试验梁受弯破坏形态如图4所示。

图4 试验梁破坏形态图Fig.4 Diagram of the failure shape of the test beam

在试验加载初期，梁全截面受力，并且应变很小，混凝土和钢筋协调受力，试件近似处于线弹性工作阶段，无肉眼可见的裂缝出现。随着外荷载的不断增加，混凝土出现塑性变形，加载至12kN左右，在梁跨中纯弯段出现第一条弯曲裂缝。随着施加荷载的逐渐增大，在12kN～40kN，由于受拉区混凝土开裂并退出工作，跨中段弯曲裂缝数量不断增加，并且沿着垂直方向向上延伸，裂缝宽度逐渐增大，同时，在剪弯段也出现数条裂缝。在40kN～50kN左右，试验梁受弯段钢筋屈服，试验梁抗弯刚度减小，跨中挠度增长迅速，裂缝沿梁截面高度方向不断向上发展，最终贯通梁全截面，达到试验梁的极限承载力，试验梁破坏。

普通混凝土梁与石墨尾矿砂混凝土梁的开裂荷载(弯矩)、屈服荷载(弯矩)以及极限荷载(弯矩)如表3所示。

表3 加载试验结果图

2.2 平截面假定验证

平截面假定是混凝土结构计算的一个基本依据，对于石墨尾矿砂混凝土，其力学性能较普通混凝土有所不同，为满足石墨尾矿砂混凝土正截面承载力的计算条件，就需要确定石墨尾矿砂混凝土是否符合平截面假定。

图5为不同石墨尾矿砂掺量的钢筋混凝土梁在不同荷载作用下，跨中混凝土应变沿梁截面高度的变化情况，以此来验证石墨尾矿砂混凝土梁对平截面假定的适用性。从图5中各试验梁跨中截面不同高度测点的应变可知，不论石墨尾矿砂的掺量是多少，正截面上各测点的应变与该点到中性轴的距离近似成正比，跨中截面上各测点的混凝土应变基本呈线性分布，这一规律说明，石墨尾矿砂混凝土梁基本符合平截面假定，可以作为其正截面受弯承载力计算的理论依据。

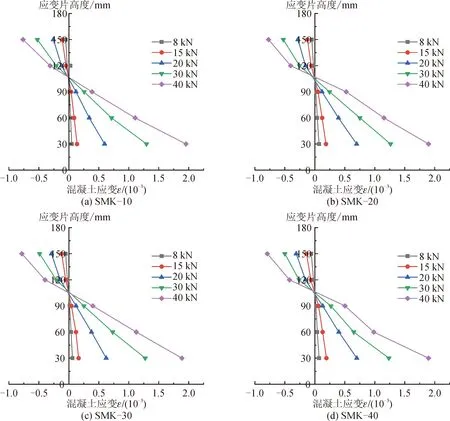
图5 试验梁跨中不同截面高度应变分布Fig.5 Strain distribution in the mid-span section of the test beam

2.3 跨中挠度分析

实测各试验梁荷载-挠度曲线如图6所示，试验梁在破坏形态上的差异可以在荷载-挠度曲线中得到直观的反映。

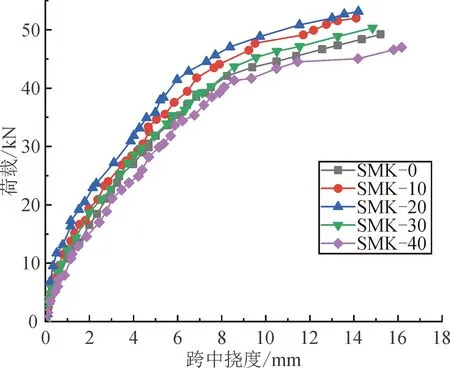
图6 荷载-挠度曲线Fig.6 Load-deflection curve

从图6中可以看出，石墨尾矿砂混凝土梁的荷载-挠度曲线和普通混凝土梁的趋势基本一致。在试验加载初期，梁处于弹性阶段，曲线近似为直线，随着荷载继续施加，试验梁开始出现裂缝，荷载-挠度曲线出现转折点，挠度增长的速度逐渐加快，且开裂后荷载-挠度曲线逐渐呈非线性发展，刚度显著降低。荷载逐渐加大至钢筋屈服，荷载-挠度曲线出现第二个转折点，屈服后梁的挠度激增，当荷载增加较少时，挠度增大很多，荷载-挠度曲线也近乎水平直线，最终试验梁破坏。

具体来看，随着石墨尾矿砂取代率的增加，试验梁的极限承载力先升高后降低。石墨尾矿砂取代率为10%、20%和30%时，石墨尾矿砂混凝土梁均比普通混凝土梁的极限承载力大，SMK-10、SMK-20比SMK-0分别增加了5.60%、7.94%，其中，SMK-20增加最多，说明取代率为20%的石墨尾矿砂混凝土梁抗弯性能最好，这可能是由于石墨尾矿砂取代率为10%～20%时，石墨尾矿砂增加了混凝土的致密性，提高了石墨尾矿砂混凝土的强度，当石墨尾矿砂取代率为20%时，混凝土试块的总孔隙率、总孔体积和比表面积全部达到最优，因此混凝土试块的抗压强度达到最优[2]。取代率为40%时，石墨尾矿砂混凝土梁的极限承载力稍低于普通混凝土梁，SMK-40比SMK-0降低了4.55%。关于极限挠度，当取代率为10%、20%和30%时，石墨尾矿砂混凝土梁均比普通混凝土梁小，SMK-10、SMK-20、SMK-30比SMK-0分别降低了7.30%、6.64%、2.43%；当取代率为40%时，石墨尾矿砂混凝土梁的极限挠度比普通混凝土梁的挠度大，增加了6.25%。

3 极限弯矩及跨中挠度计算

3.1 极限弯矩试验值及计算值对比分析

根据以上分析，石墨尾矿砂混凝土梁正截面试验满足受弯构件正截面承载力计算的基本假定，但目前并没有石墨尾矿砂混凝土结构的设计规范，因此参照《混凝土结构设计规范》(GB 50010—2010)[19]中的承载力计算公式，对石墨尾矿砂混凝土梁极限承载力进行计算，梁正截面承载力为：

Mu=α1fcbx(h0-x/2)

(1)

α1fcx=fyAs

(2)

式中：α1为受压区混凝土的简化应力图形系数，取1.0；fc为石墨尾矿砂混凝土轴心抗压强度，取实测值，MPa；b为梁宽，mm；x为截面受压区高度，mm；h0为截面有效高度，mm；fy为纵筋屈服强度，取实测值，MPa；As为受拉纵筋有效截面面积，mm2。

由式(1)和(2)计算各试件抗弯极限承载力Mu及试验值Mc，如表4所示。

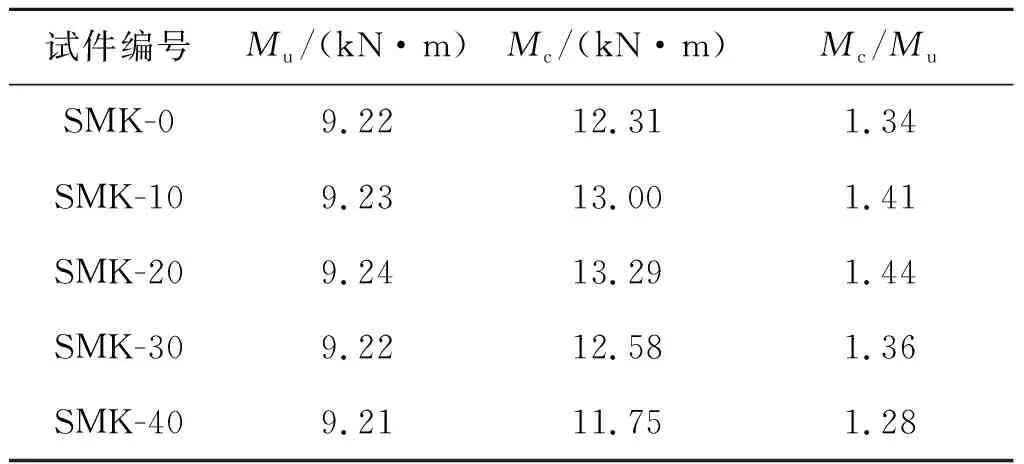
表4 极限承载力计算值与试验值对比

由表4可知，石墨尾矿砂混凝土梁与普通混凝土梁的试验值均大于计算值，说明按照混凝土规范计算石墨尾矿砂混凝土梁的极限承载力是可行的，但是偏于保守。

然而，现行规范中的计算公式没有考虑石墨尾矿砂取代率的因素，所以不同石墨尾矿砂掺量的混凝土梁的计算值可能会出现误差，因此引入石墨尾矿砂取代率的修正系数。参照李志强等[15]的方法，对不同石墨尾矿砂取代率的混凝土梁的数据进行数值拟合，拟合曲线如图7所示。其中，拟合曲线的决定系数R2为0.970 2，表明曲线的拟合优度高。

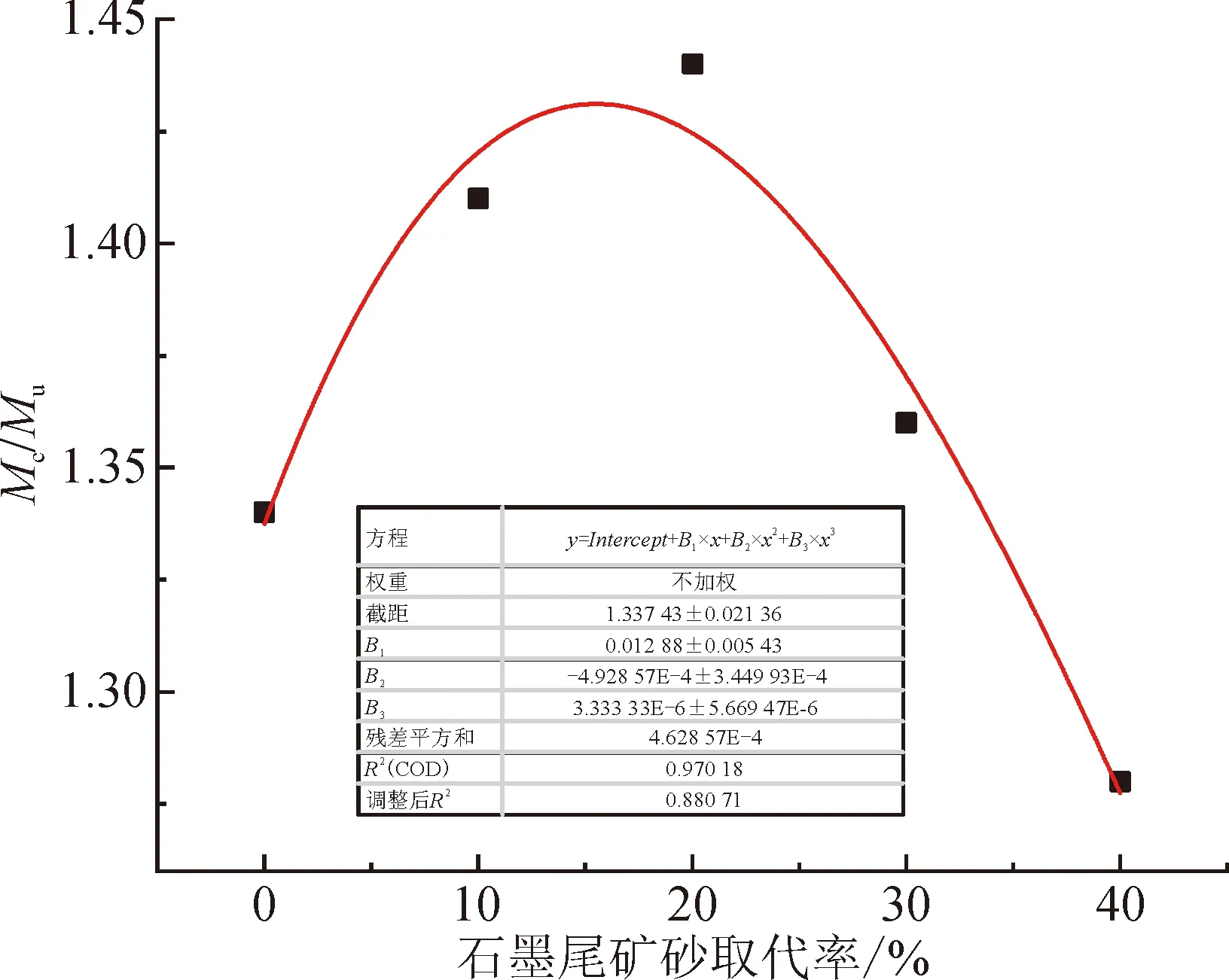
图7 拟合曲线Fig.7 Fitting curve

根据拟合曲线，可以提出石墨尾矿砂混凝土梁的正截面极限承载力计算公式：

M=yMu=(B1x2+B2x+C)Mu

(3)

式中：M为修正后梁的极限承载力，MPa；y为修正系数；Mu为梁的极限承载力理论计算值，MPa；x为石墨尾矿砂取代率，%；B1=-0.000 321 4，B2=0.011 16，C=1.339 7。

利用式(3)计算石墨尾矿砂混凝土梁的极限承载力M，并与梁极限承载力试验值Mc进行对比，如表5所示。同时，利用式(3)，还可预测不同质量取代率的石墨尾矿砂混凝土梁的极限承载力。

由表5可知，Mc/M的平均值为0.999 2，说明修正后的计算值与试验值吻合较好，表明修正后的极限承载力计算公式适用于石墨尾矿砂混凝土梁的极限承载力计算。

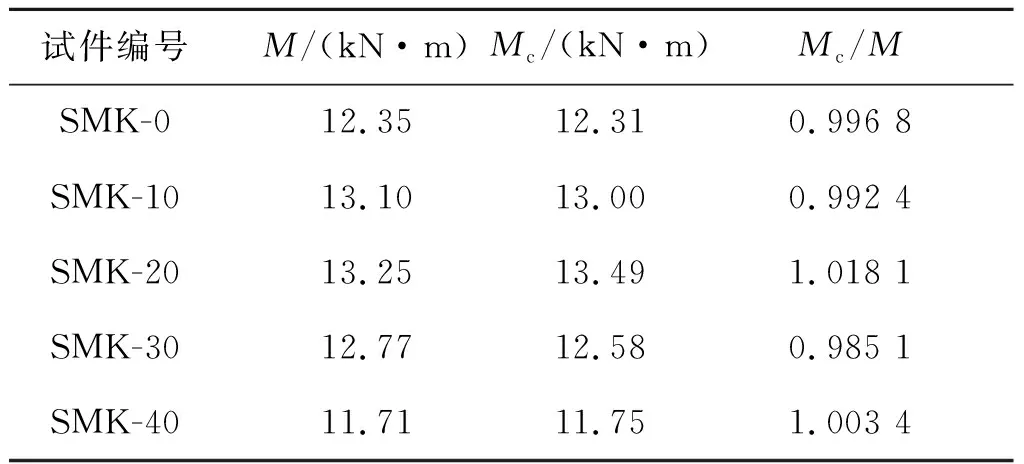
表5 修正后的极限承载力计算值与试验值对比

3.2 跨中挠度试验值及计算值对比分析

采用结构力学方法计算试验梁受弯挠度，表达式为：

(4)

式中：α是与荷载的加载方式、约束条件有关的系数，对于承受三分点加载的简支梁，α取0.106 5；l0为试验梁净跨长，mm；Bs为短期刚度值，根据《混凝土结构设计规范》(GB 50010—2010)[19]和最小刚度原则，对于矩形截面混凝土梁，有：

混凝土开裂前，混凝土梁类似于弹性材料梁，其刚度基本是常数：

Bs=0.85EcI0

(5)

式中：Ec是混凝土弹性模量；I0为换算截面惯性矩，矩形截面I0=ab3/12，a为截面长，b为截面高。

裂缝出现后，混凝土梁的短期刚度为：

(6)

式中：Es是钢筋弹性模量；ψ为钢筋应变不均匀系数；αE为钢筋弹性模量与混凝土弹性模量的比值；ρ为纵向受拉钢筋配筋率。

按上式计算混凝土开裂前以及开裂后至钢筋屈服前的挠度，并与不同掺量石墨尾矿砂混凝土梁的实测挠度值进行对比，如图8所示。

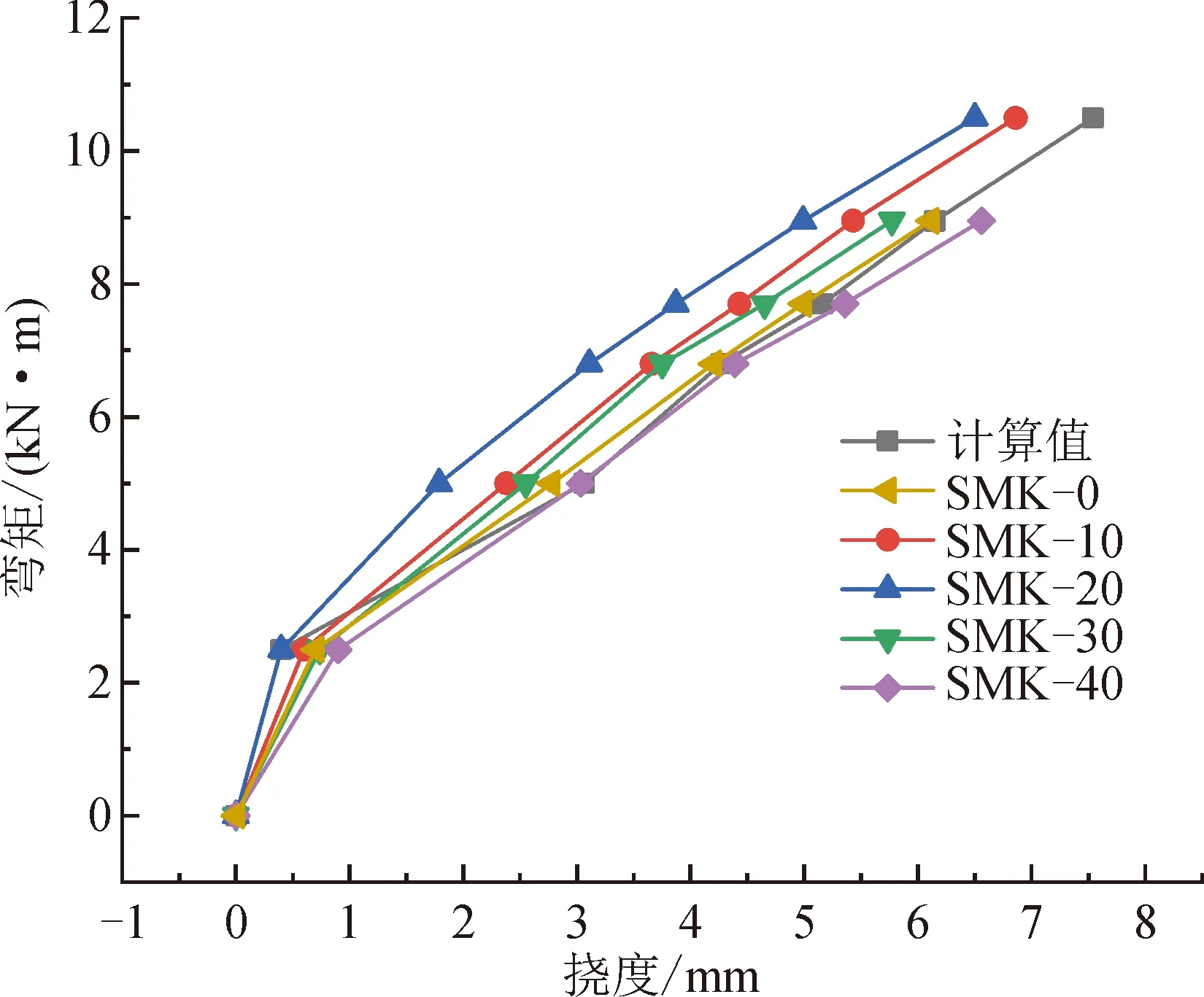
图8 挠度计算值与实测值对比图Fig.8 Comparison of calculated and measured deflection values

从图8可以看出，无论石墨尾矿砂掺量为多少，在试验梁开裂之前，挠度的实测值均比计算值稍大；在试验梁出现裂缝以后，普通混凝土梁和SMK-40梁的挠度实测值与计算值相差不大，而SMK-10、SMK-20、SMK-30梁的挠度实测值均比计算值小，这说明普通钢筋混凝土梁的挠度计算方法并不适用于石墨尾矿砂混凝土梁的挠度计算，因此，引入正常状态下不同质量取代率石墨尾矿梁的跨中挠度修正系数。对弯矩为5.1 kN·m、6.8 kN·m、7.7 kN·m、8.9 kN·m的各取代率石墨尾矿砂混凝土梁的实测挠度值与计算值的比值进行拟合，拟合曲线如图9所示。

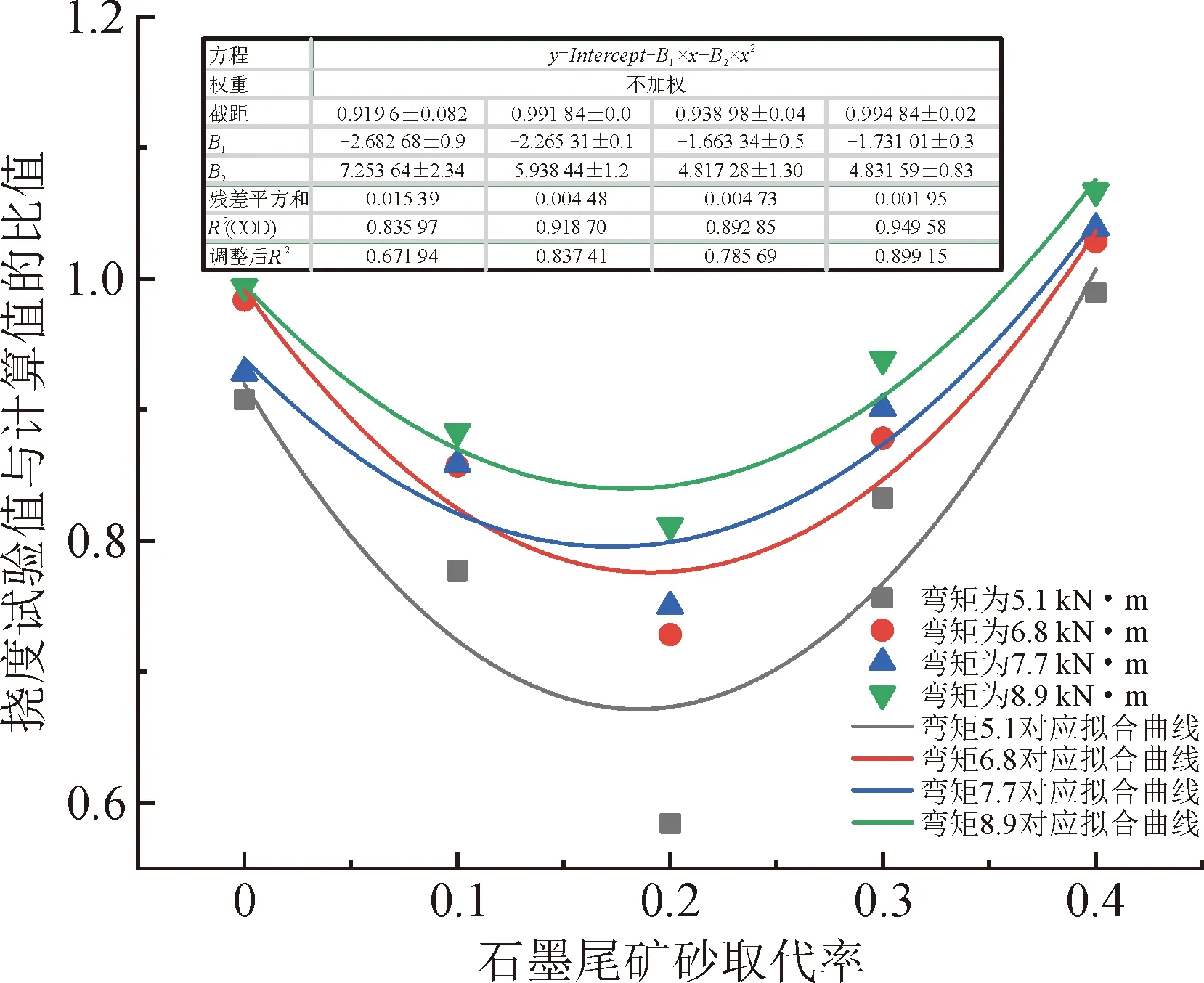
图9 挠度拟合曲线Fig.9 Deflection fitting curve

根据挠度拟合曲线，可以提出挠度修正系数η：

η=y=D1x2+D2x+E

(7)

式中：x为石墨尾矿砂取代率，%；y为修正系数。

不同弯矩作用下，修正系数的相关系数D1、D2、E以及拟合曲线的决定系数R2如表6所示。

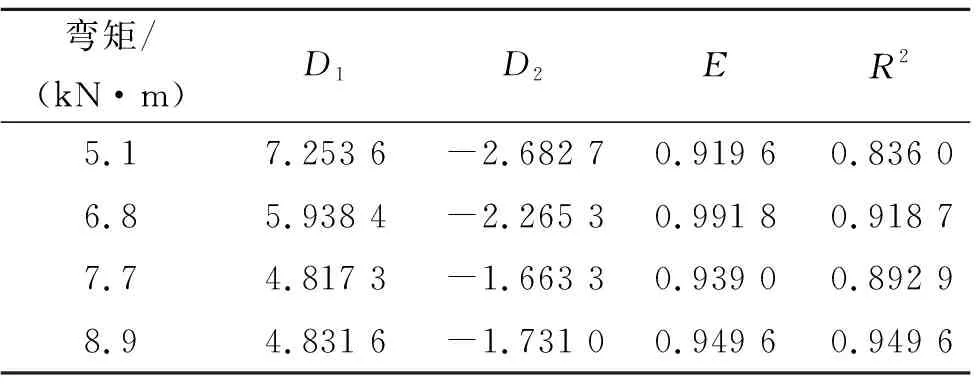
表6 修正系数η的相关系数

4 结 论

通过对不同石墨尾矿砂掺量的钢筋混凝土梁进行抗弯性能试验研究，得出以下结论。

1) 石墨尾矿砂混凝土梁的破坏形态、裂缝发展均与普通混凝土梁相似，会经历明显的线弹性阶段、裂缝发展阶段、纵筋屈服阶段以及破坏阶段。同时，石墨尾矿砂混凝土梁符合平截面假定，可以作为试验梁极限承载力理论计算的基础。

2) 石墨尾矿砂混凝土梁的荷载-挠度曲线与普通混凝土梁的发展趋势基本一致。随着石墨尾矿砂取代率的增加，试验梁的极限承载力先增大后降低，其中，石墨尾矿砂取代率为10%、20%、30%时，该梁的极限承载力均比普通混凝土梁高，而当取代率为10%～20%时，试验梁的抗弯性能最优。

3) 现行规范中的混凝土梁极限弯矩计算公式不适用于10%～40%取代率的石墨尾矿砂混凝土梁，本文通过将试验数据与理论计算数据进行拟合，提出了石墨尾矿砂混凝土梁极限弯矩的修正公式，并将修正后的数据与试验数据进行对比，发现吻合较好，基本可以满足10%～40%石墨尾矿砂混凝土梁的极限弯矩的要求；现行规范中的跨中挠度计算公式也不适用于10%～40%石墨尾矿砂混凝土梁，因此本文引入了挠度修正系数η。