海底沉积物纵波速度与强度参数关系模型研究
2022-09-25张东昱甫杨进王欢欢李潇徐飞
张东昱甫,杨进*,王欢欢,李潇,徐飞
( 1. 中国石油大学(北京) 安全与海洋工程学院,北京 102200)
1 引言
海底沉积物是海床以下区域沉积地层土的总称,与底部海水相连接,其类型多样且复杂,与区域环境、沉积作用过程等因素相关。随着石油的勘探与开发逐渐转向深海,熟悉与确定海底沉积物特性变得尤为重要。
海底沉积物的强度参数与海上平台插桩就位、导管架的安装等工程关系密切,与海上作业安全息息相关。常规强度参数的获取主要通过海底钻孔取芯或静力触探技术(Cone Penetration Test)来完成。钻孔取芯法发展较早,根据沉积物的种类与取样器类型等因素划分出不同的取样方式[1-2]。虽然此方式钻入深度范围广,但钻孔数量较少,而且钻孔对于沉积物的扰动较大,导致强度参数精度较差。相较于钻孔取样方法,静力触探法能提供高分辨率的原位测试数据[3],具有快速性、可靠性等特点,但其成本较高,应用局限性较大。所以亟需一种准确、便捷、低成本的海底沉积物强度参数获取方法。
在海洋石油钻井中,地球物理勘探是一种非常成熟的研究手段。依据地震资料可以获得海底沉积物的声学信息,如声波速度、声衰减等。其声学特性的分布是海域声场环境的重要组成部分,也是进行海洋多波束或浅地层精细解释的基础资料[4]。目前,获取海底沉积物声学参数的方法包括声波传播理论与经验公式的构建。其中,声波传播理论将海底沉积物视为固、液两相介质,探究介质之间运动与相互作用对声学特征的影响。Gassmann[5]考虑到沉积物颗粒之间相互摩擦,建立了饱和沉积物的声学传播公式,但没有考虑沉积物中孔隙流体与骨架的相对运动。Biot[6-8]考虑到各向异性和黏弹性的问题,建立了流体饱和多孔介质弹性波波动方程。Buckingham[9-10]提出了一种颗粒间耗散形式,建立了新型声波传播理论。经验公式法是基于海域原位测量结果,建立符合本区域特征的沉积物物性与声学特征的关系。Hamilton[11]根据北太平洋沉积物的资料,建立了声速与孔隙度、密度、黏土含量等参数的经验公式。侯正瑜等[12]依据南沙群岛海域沉积物资料,建立声速与孔隙度等参数的经验公式。Zheng等[13]采用不同频率的声学测量手段,建立了声速与含砂量等参数的经验公式。Kim等[14]建立了韩国海区声速与平均粒径等参数的经验关系。
考虑到海域地震资料的声学响应特征,探究土体声学与强度特性之间的关系,是在缺乏原位数据情况下,获取沉积物强度参数的有效方式。Duan等[15]建立了江苏地区土体横波速度与抗剪强度、有效应力间的关系,黄雅虹等[16]建立了渤海黏土的横波速度与抗剪强度的关系。但原位测量具有地域局限性,建立的相互关系仅仅符合本区域的特点,难以将关系模型进行外部拓展。
本文基于南海沉积物的实际资料,在室内制备不同物性参数(密度、孔隙度)梯度的小尺寸模拟地层,并用声波仪器测取不同模拟地层的纵波速度。依托于声波理论传播模型,带入预设参数求解理论波速,并与实际配置模拟的纵波速度进行对比与验证。采用室内土力学试验测量强度参数,探究海底沉积物声学特性与强度参数的关系,建立基于声学特征的海底沉积物强度参数预测模型,有效提高无法取样地区地层强度参数的精度,为浅层钻井提供理论技术支持。
2 沉积物声学传播理论
因为声波波长远大于沉积物颗粒尺寸大小,因此将海底沉积物视为连续介质。研究初期,多数学者用基质颗粒与孔隙流体两相组分体积模量和密度的加权平均数表示纵波速度,代表理论为Wood方程[9]。此后Stoll[17]在Biot的饱和多孔介质声波传播模型基础上,加入了两相组分位移活动的影响。Dvorkin等[18]和Helgerud等[19]考虑到骨架和基质颗粒间的关系,对弹性模量进行了进一步修正,建立了等效介质理论。
2.1 Wood理论模型
海底沉积物是一种两相介质,由基质颗粒和孔隙流体组成,在粒间没有摩擦耗散的情况下,纵波速度与两相介质的体积模量和密度相关,计算公式为

式中,Vp为纵波速度;K0为两相介质体积模量;ρ0为两相介质密度。
两相介质的体积模量与密度计算公式为
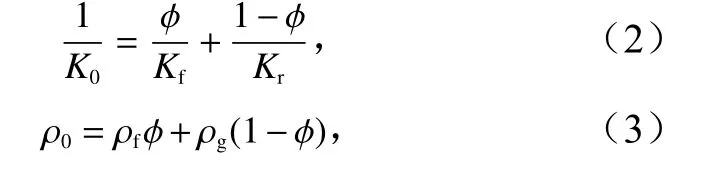
式中,Kr为基质颗粒体积模量;Kf为孔隙流体体积模量;ρf为孔隙流体密度;ρg为基质颗粒密度;ϕ为孔隙度。带入式(1)可求得纵波速度为

2.2 Biot-Stoll理论模型
Stoll在Biot模型基础上提出了多孔介质模型,考虑到了介质的孔隙性与弹性。对于海底沉积物,多孔弹性理论模型可以很好地模拟实际情况。Stoll根据可测量的沉积物特性推导出Biot模量的表达式为
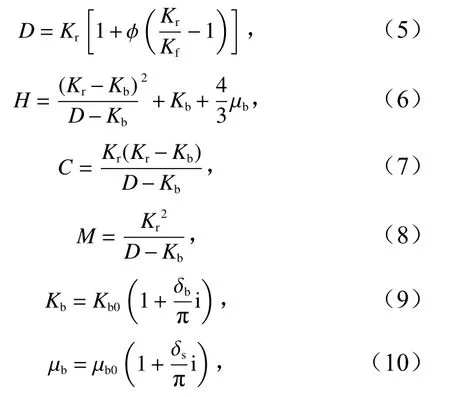
式中,D为中间变量;H为弹性模量;C为附加弹性模量;M为复弹性模量;Kb为骨架体积模量(复数);i为虚数单位;µb为骨架剪切模量(复数); δb为体积衰减系数;δs为剪切衰减系数;骨架体积模量实部Kb0,骨架剪切模量实部µb0,渗透率κ是根据土体本身性质得出[20],推导公式为
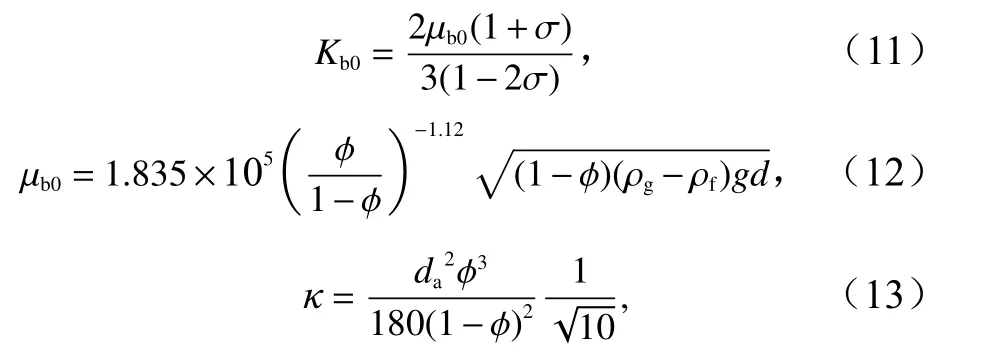
多孔介质中的简谐平面波传播的表达式为
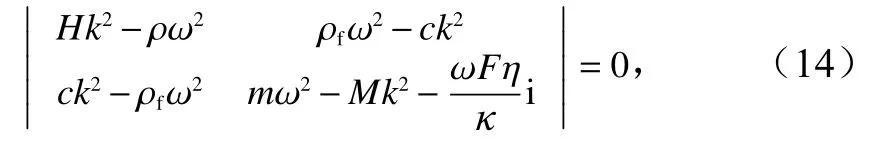
式中,σ为泊松比;g为重力加速度;d为模拟深度;da为平均粒径;k为复波数;ρ为实际密度;ω为角频率;F为黏性校正系数;η为绝对黏度;m为考虑了流体流动相对于宏观压力梯度的相位;c为曲折度,其中,

求解上述方程,得到以k2为基底二次型方程,利用求根公式解出复波数k并取其实部,带入下式即得纵波速度:

2.3 Dvorkin等效介质理论模型
Dvorkin提出等效介质理论,建立了骨架与基质颗粒之间的关系,是饱和多孔介质理论的补充[18-19]。沉积物骨架的弹性模量与孔隙度、基质颗粒弹性模量、有效应力等因素相关。以临界孔隙度ϕc为基准分别建立不同情况下干骨架弹性模量的计算公式。
当实际孔隙度大于临界孔隙度时:

式中,Z为中间系数,当实际孔隙度小于临界孔隙度时:
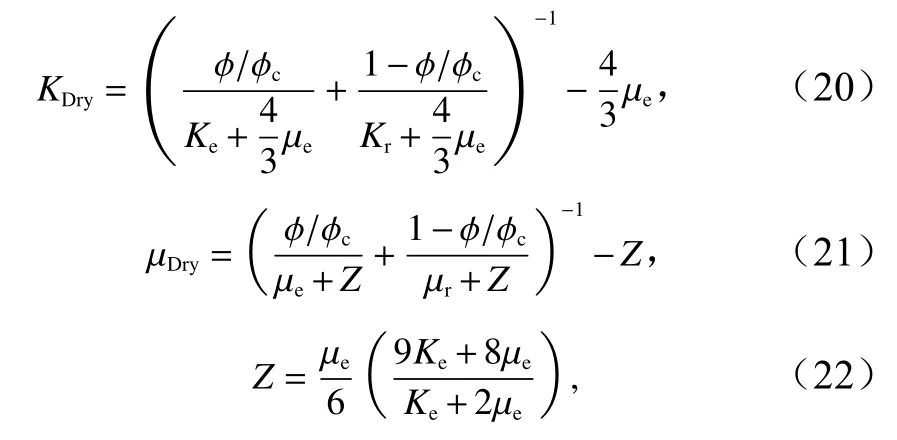
有效骨架体积模量Ke,有效骨架剪切模量µe,有效应力P表达式如下:

式中,KDry为干骨架体积模量;µDry为干骨架剪切模量;µr为基质颗粒剪切模量;n为每粒颗粒的平均接触次数。
由于海底沉积物是饱和多孔介质,Gassmann[5]建立了流体饱和体积模量Ksat与孔隙流体体积模量、干骨架体积模量等参数之间的关系。流体饱和体积模量Ksat会随着流体的性质而改变,但流体饱和剪切模量µsat是不变的,公式为
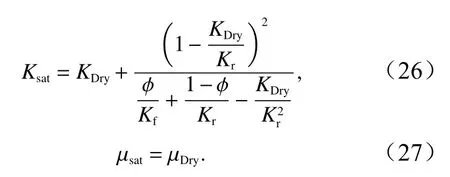
根据弹性介质理论,纵波速度与流体饱和体积模量、剪切模量和密度相关,公式为

2.4 理论模型参数选取
本文的参数选取中,密度和孔隙度根据实际土样配置情况得到,实验的孔隙流体为水,则流体密度和体积模量参考常温下水的数值。基质颗粒体积模量、基质颗粒剪切模量、泊松比、渗透率、临界孔隙度等其余数值参考经验公式与几位学者预设数值[4,9,18,20],并结合实际情况与实验特性进行微调(表1)。

表1 声波传播理论参数Table 1 Parameters of the theory of acoustic propagation
3 室内模拟实验
3.1 实验背景
从横向上看,南海北部大陆架近岸以粉砂质黏土和黏土质粉砂为主,向外延伸至混合沉积区,以粉砂、黏土质砂和砂质黏土为主,至陆架外缘沉积物以细砂分布为主。在纵向上,通过钻孔数据表明,浅部地层上段主要为黏土质粉砂[21]。对于南沙群岛附近沿海大陆架海域,其粉砂含量范围为38.16%~70.73%,均值为55.37%[22],粉砂和黏土是南海沉积物的重要组成部分。在物性参数方面,孔隙度为海底沉积物孔隙体积与总体积的比值,南海北部大陆架沉积物的密度范围为1.48~1.92 g/cm3,均值为1.70 g/cm3[23],孔隙度为27.2%~69.7%,均值为53.3%。海南岛东南外海域沉积物密度范围为1.414~1.648 g/cm3,均值为1.565 g/cm3,孔隙度为44.77%~77.35%[24]。南海南沙群岛海域沉积物密度为1.46~1.83 g/cm3,孔隙度为50.36%~58.56%[25]。海上原位取样测量因受土体失水等因素影响,造成土质样品受扰动,数据与实际情况偏差较大,并且成本较高。而室内模拟实验可以避免上述问题,按梯度模拟沉积物物性参数范围。通过南海实际沉积物物性参数调查,为实验开展提供数据支持。
本实验采用EDJ-1电动应变直剪仪与微型十字剪切板测量强度参数。声波测量装置采用北京中拓科仪公司ZT802型声波测试仪,声波换能器频率为50 kHz,通过内置计算机与声波测量装置相结合,可进行声波数据的记录与处理。声学与强度参数测量在一个规格为35 cm×20 cm×30 cm的测试箱中进行,箱侧边均标有刻度线,内壁贴有泡沫板作为吸声装置,可防止声波在壁面反射,影响实验效果。将声波换能器分别置于箱底部两侧,将配置好的土样填入制样箱中,进行纵波速度的测量。装置示意图如图1。
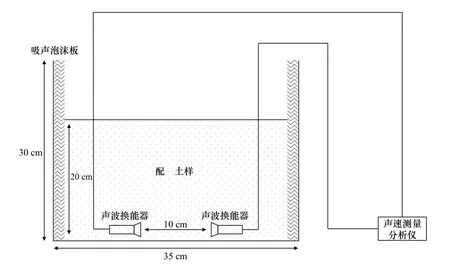
图1 声波测量装置Fig. 1 Acoustic measuring device
3.2 实验步骤
选取100目的石英砂作为砂土部分,选取1 250目的膨润土作为黏土成分,为保持土质的一致性与减少误差,一次性备置足量土样。其中,砂土占总质量的60%,黏土占总质量的40%,通过改变孔隙比与密度的大小,根据公式在测试箱中分别添加不同质量的基础土样和水,保持含水率固定在20%[26]。为充分模拟海底沉积物特性,加土的同时使用洒水壶均匀浸润土样,并击实土样以排出孔隙中的空气。土水添加完成后使用压实装置对土样充分压实到同一高度(20 cm),使实验土样的体积保持一致。填充完成后立即用保鲜膜紧密盖住土样,将土样静置6 h,使其水分充分均匀渗透进孔隙中。
配置完成后根据密度公式计算土样的密度,配置10组不同密度的土样(表2),相关公式为

式中,ms为添加土的质量;mω为添加水的质量;ρs为颗粒密度;e为孔隙比;ω0为风干土含水率;ω为设计含水率;V为土样体积。
为了防止土样受剪切发生扰动,先进行声学测量。将声波换能器分别置于箱底部两侧,间距保持10 cm,填土前在换能器上涂抹凡士林使其与土样充分耦合。在箱中对每一组样品进行声波速度的测量,通过测量发射端与接收端信号接收时间,计算出土样的声速。为减小误差,每组土样测量3次取其平均值。其声波测量原理为
累积型指标常见于民生类指标,如新增就业人口,新建保障房等。该类型指标的规划目标为累积增加值或累积减少值。记Ni为第i年的实际值,N为五年期末规划值,计算公式:com_


表2 实验土样基本配置情况Table 2 Basic configuration of experimental soil
式中,d1为两个声波换能器的间距;Δt为发射端与接收端的时间差。
参照土工试验方法标准(GB/T 50123-2019)测量强度参数。首先使用微型十字剪切板测量不同密度土样的抗剪强度,继而使用环刀法对土样进行取样,在不同垂向压力(50 kPa、100 kPa、150 kPa、200 kPa)条件下进行直接剪切试验,采用快剪法并使用较快速度的水平剪切速度(0.8 mm/min)剪切,当剪应力数值达到峰值时,记录土样在不同压力条件下抗剪强度。建立垂向压力与抗剪强度坐标轴,依据库伦公式计算出每组土样的内摩擦角和黏聚力数值。
4 结果分析
4.1 声学特性分析
将3种声学理论传播模型带入预设参数求解出纵波速度,为控制误差大小,密度孔隙度换算关系参考Liu等[27]对于海底沉积物的原位测量规律,公式为

3种声学传播模型声波速度随着密度的变化趋势相似,密度为1.7 g/cm3区域为临界点,小于此密度时声速保持不变或增加缓慢,超过此密度后声速增加趋势较剧烈。原因在于,密度较小区域,孔隙度较大,孔隙内流体含量较多,密度增加带来的孔隙变化对于土体模量的影响甚微,声速变化不大。随着密度达到一定数值,声波传播主要通过土体的固相框架进行,而密度增加带来孔隙度的变化,会急剧影响土体的模量变化,声速会随着密度的增加急剧升高。相较于其他两种模型,Wood模型求解出的声速较高,密度为1.9 g/cm3时较Biot-Stoll模型高15.9 m/s,较Dvorkin模型高5.8 m/s。虽然Wood模型没有考虑到颗粒间的能量耗散,但与其余两种模型的最大差值仅为1.12%和0.47%,可见物性参数中的密度对于声学传播模型的敏感度较低。
基于室内模拟实验,将室内实测纵波速度与理论模型计算速度进行对比,验证室内实验的准确性(图2)。结果表明,两者曲线趋势相似,当密度小于1.75 g/cm3时,实测值与理论值契合度较高,大于1.75 g/cm3时,实测值略高于理论值。原因在于,当密度大于一定数值时,声速的变化主要依赖于土体的模量变化,但理论模型对于模量变化的估计存在局限性,使其相较于实测数值较小。但考虑到整个密度区间,实测声速与Dvorkin模型求解声速的最大差值为2.91%,与Biot-Stoll模型的最大差值为3.52%,与Wood模型最大差值仅为2.47%。总体来看,室内模拟实验得出的声波速度符合声波理论传播模型。

图2 声波理论模型结果Fig. 2 Results of theoretical model of acoustic wave
因本文的3种理论模型较为复杂,参数众多且相互影响,无法根据模型建立物性参数与纵波速度的单一参数模型。基于Gardner等[28]和Castagna等[29]提出的地层密度与纵波速度的经验模型,带入实测数值进行公式拟合,得到室内模拟沉积物的纵波速度与物性参数关系(表3),因实测声速契合声学理论传播规律,此关系模型具有准确性。
4.2 强度特性分析
基于室内土力学试验结果,建立不同密度土体直接剪切试验三维图(图3)。图像整体呈斜面趋势,远端高近端低。密度保持一致的条件下,抗剪强度与垂向压力呈正相关。密度为1.8 g/cm³时,垂向压力自50 kPa增加至200 kPa,抗剪强度分级增长16.14 kPa、20.59 kPa、16.68 kPa。同样,当垂向压力保持一致的情况下,随着土质密度的增加,抗剪强度虽有小幅波动,但整体也逐步增加。对于不同孔隙度土体的试验结果(图4),当垂向压力不变时,孔隙度与抗剪强度呈反比的关系。垂向压力为100 kPa时,不同孔隙度土体中抗剪强度的最大差值为17.34 kPa。垂向压力为200 kPa时,最大差值为27.76 kPa。原因在于,模拟土体的密度与孔隙度呈负相关关系,随着土质密度的增加或孔隙度的减小,或是垂向压力的增加,单位体积内的土质变得更加密实,土质颗粒关系愈加紧凑,咬合作用越强,抵抗外部的剪切作用能力越强。

表3 纵波速度与物性参数关系Table 3 Relationship between P-wave velocity and physical parameters
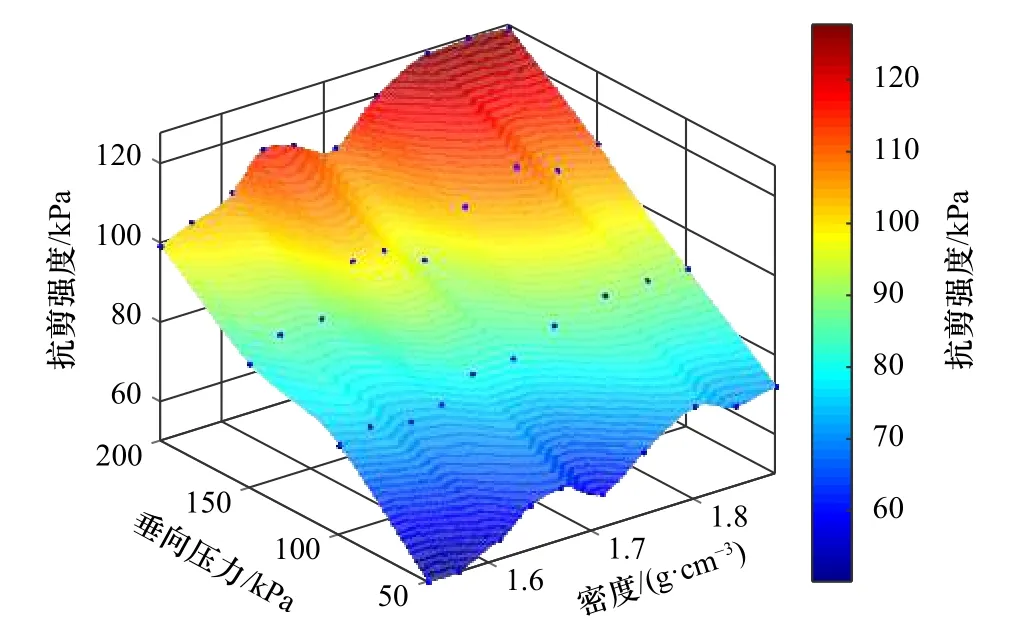
图3 不同密度土体直接剪切试验Fig. 3 Direct shear test of soil samples with different density
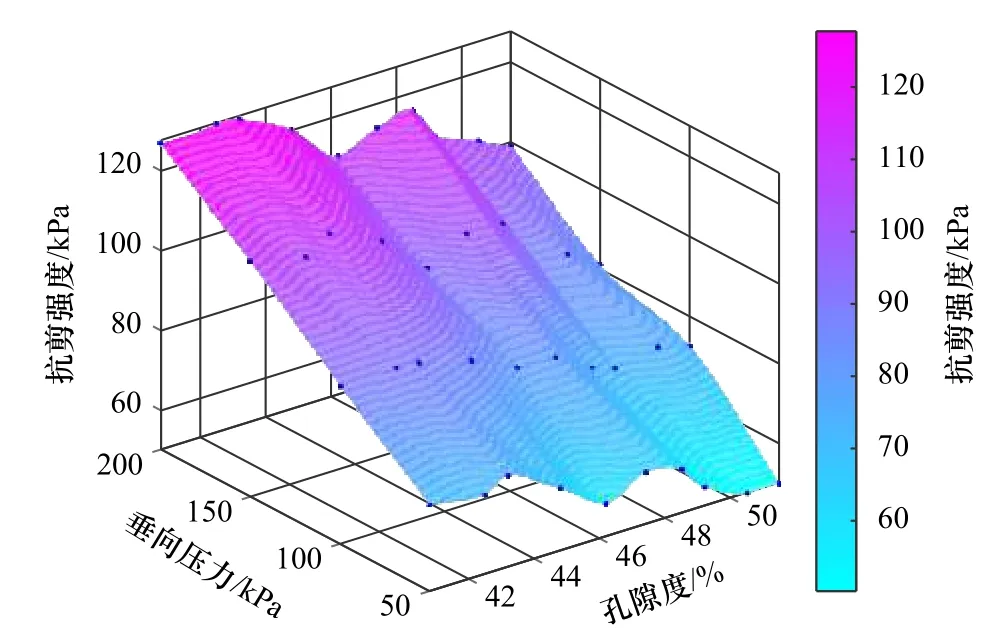
图4 不同孔隙度土体直接剪切试验Fig. 4 Direct shear test of soil samples with different porosity
建立不同密度、孔隙度与强度参数的关系(图5,图6)。其中,抗剪强度根据十字剪切板法获取,黏聚力和内摩擦角基于直剪试验结果,使用库伦公式计算得出。整体来看,随着密度的增加或是孔隙度的减小,3种强度参数均呈现增加的趋势,相较于黏聚力与抗剪强度,内摩擦角波动性较大,但基本稳定在一定数值区间。密度为1.8 g/cm3时为黏聚力的极值,孔隙度40.8%时为抗剪强度的极值。

图5 密度、强度参数与纵波速度的关系Fig. 5 Relationship between density, strength parameters and P-wave velocity
基于室内土力学试验,带入实测数值进行公式拟合,得到沉积物的强度特性与物性参数关系(表4)。其中内摩擦角与物性参数呈线性关系,抗剪强度、黏聚力与物性参数呈二次型关系。除内摩擦角以外,其余两种强度参数模型拟合程度较高。原因在于,随着密度增长,孔隙空间逐渐减小,颗粒之间愈发紧密,形成了公共结合水膜,颗粒之间的胶结作用就更加明显,颗粒接触点的化合键作用增加,使得黏聚力与抗剪强度逐步增加。土体内摩擦角受咬合摩擦与滑动摩擦共同影响,受剪切作用时,密度增加导致土体颗粒移动阻力增大,使得咬合摩擦增大。密度增加导致颗粒间接触点增多,总荷载分配到更多的接触点中,每个接触点上所承受的力就相应减小,使得滑动摩擦增加,但增加的幅度并不一致。综合两种因素可知,随着密度的增长,内摩擦角的涨幅并不均匀,导致拟合程度不高。
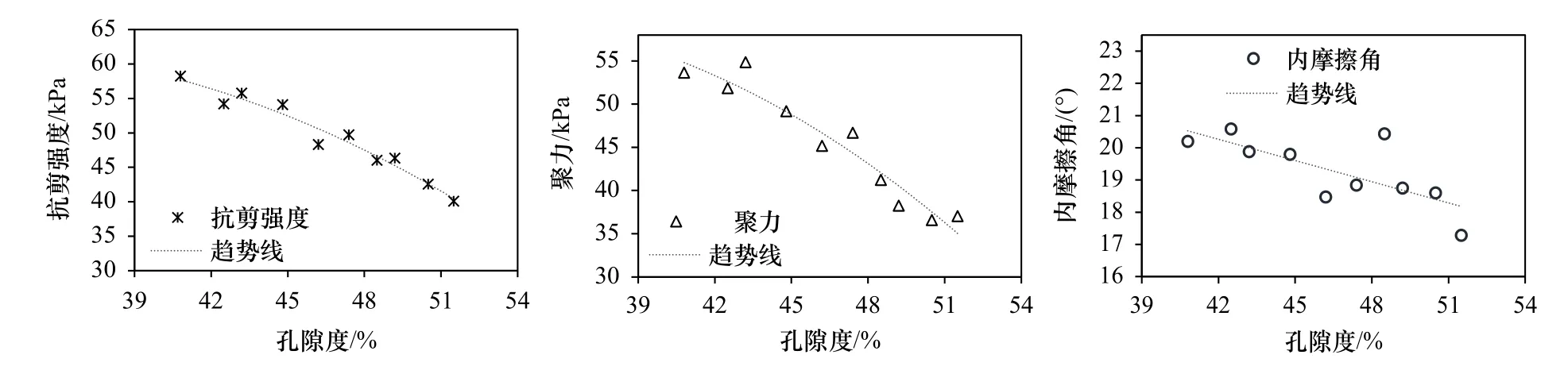
图6 孔隙度与强度参数的关系Fig. 6 Relationship between porosity and strength parameters
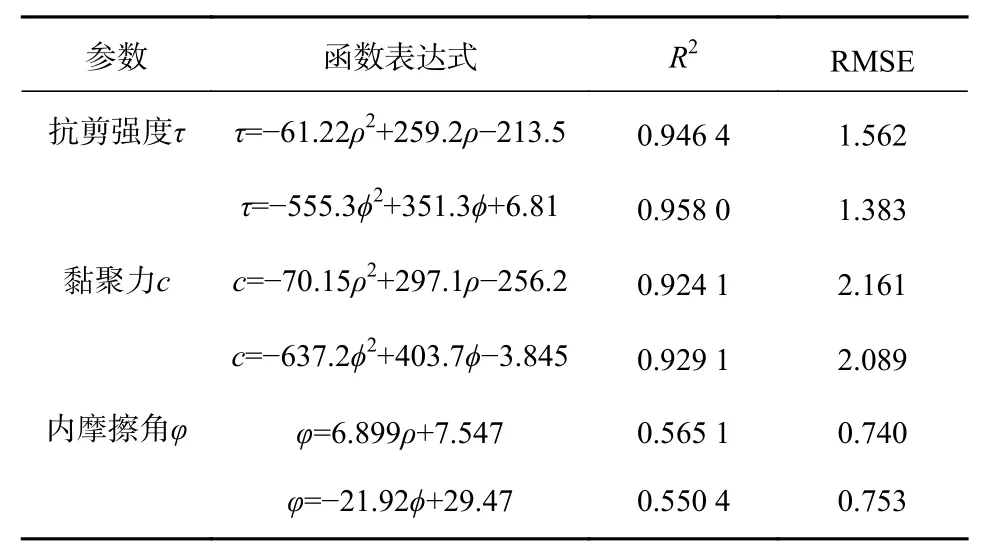
表4 强度与物性参数关系Table 4 Relationship between strength and physical parameters
4.3 沉积物强度参数预测模型
根据室内实验结果,建立强度参数与纵波速度关系(图5)。整体看强度参数、物性参数(密度)与纵波速度3种变量呈现正相关的关系,即随着其中一种变量的增加,其余两项也随之增长。随着抗剪强度增加,纵波速度呈现初期缓慢增长,中后期快速增加的趋势。在实际海域沉积物的原位测量中,随着地层深度的增加,土质抗剪强度增加,地震资料获取的层位声波时差减小,对应的纵波速度增长,这与实验结果相吻合。黏聚力与声波速度的关系趋势与抗剪强度类似,原因为土质密度增大导致密实程度较高。而内摩擦角的大小波动较为明显,与纵波速度联系不太紧密。
根据前文研究结果,土体物性参数与纵波速度的拟合型式为

强度参数与物性参数的拟合型式为

式中,a、b、a′、b′、c′均为待定系数。将式(33)带入式(34)至式(36)中,得到两种型式的强度与声学参数关系模型。其中式(37)适用于内摩擦角与纵波速度的关系式,式(38)适用于抗剪强度、黏聚力与纵波速度的关系式。
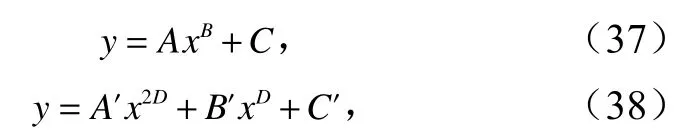
式中,A、B、C、D、A′、B′、C′均为待定系数。
将实测强度参数与纵波速度带入公式进行拟合,得到基于声学特性的强度参数预测模型(表5)。此模型将物性参数作为中间变量,直接建立强度参数与纵波速度的关系。在海洋石油钻井中,地球物理资料较易获取,所以沉积物的声学资料较为完备,且涉及范围较大。但强度参数往往是通过钻孔取芯或是原位静力触探获取,受生产成本、工作效率等影响,强度参数较为缺乏,且局限于几个点。在现场应用中,基于地球物理方法获取的声学资料,直接代入预测模型可直接求取此区域工程强度性质,节约了成本,提高了经济效益。

表5 强度参数预测模型Table 5 Prediction model of strength parameters
因原位测量存在土体失水扰动和应用范围较窄等问题,室内测量可以充分控制土体的物性参数,建立不同梯度参数条件下声学特性与强度参数的联系。
此方法基于土体本身物性参数性质,且通过声波理论传播模型的验证,具有普适性与准确性,对于浅层的勘探与开发起到了理论指导的作用。
此外,相关模型还可用于海底浅层地质灾害预测。如已知区块的声学与强度参数资料符合上述预测模型,则代表此处区域没有浅层地质灾害。反之,若实测资料与模型偏差较大,则表明此处海底沉积物区域可能存在浅层气或浅水流等地质灾害。
5 结论
(1)基于3种声波传播模型,带入预设参数求解纵波速度,比较了不同理论模型之间声速的差异。结果表明,3种模型变化趋势相似,均与土体密度呈正相关的关系,原因在于密度变化引起的土体模量变化,导致声速改变。相较于其他两种理论,Wood模型理论声速偏高,但模型之间声速差值较小,物性参数中的密度对于声波传播模型的敏感度较低。
(2)室内实验测量值与理论模型计算值的对比分析表明,实测声速与理论模型中Biot-Stoll模型的最大误差为3.52%,与Wood模型的最大误差仅为2.47%,室内测量结果符合理论模型趋势,契合度较高。基于Gardner方程与实测数据,建立模拟海底沉积物地层纵波速度与物性参数的关系模型。
(3)室内土力学试验结果表明,随着密度增加或孔隙度减小,抗剪强度和黏聚力的数值逐渐增大,而内摩擦角趋势不太稳定。原因在于,密度增加使得单位体积内的土质更加密实,颗粒关系愈加紧凑,胶结作用明显,导致抗剪强度和黏聚力增加。而内摩擦角受土体咬合摩擦与滑动摩擦共同影响,密度增加导致土体颗粒移动阻力增大,颗粒间接触点增多,总荷载分配到更多的接触点中,每个接触点上所承受的力就相应减小,使得内摩擦角数值增加,但增加的幅度并不一致,导致拟合程度不高。基于实测数据,建立了模拟海底沉积物地层强度特性与物性参数的关系模型。
(4)将物性参数作为中间变量,建立基于声学特性的强度参数预测模型。因实际海域声学资料易获取且较为完备,将实测声速直接带入模型中,可直接求解目标区块的强度参数。此预测模型分梯度控制了土体的物性参数,既避免了原位测量土体失水扰动的问题,又弥补了经验公式地域局限性的缺点,具有普适性与准确性,有效提高了无法取样海域土质强度参数的精度,节约了成本,提高了经济效益,对于浅层的勘探与开发起到了理论指导的作用。
