基于黄金莱维引导机制的阿基米德优化算法
2022-09-25何庆李守玉
陈 俊,何庆,李守玉
(贵州大学大数据与信息工程学院,贵阳 550025)
0 引言
近年来随着科学技术,特别是电子信息技术的飞速发展,全局优化方法在电力调度[1]、控制工程[2]、图像处理[3]、生物医学信号处理[4]等众多领域的应用越来越广泛;然而对于非线性以及目标函数不可导的全局优化问题,传统的优化方法很难在合理时间内解决。利用类似仿生学原理,将自然、动物的一些现象抽象成的算法——元启发算法[5-13]为解决复杂全局优化问题提供了一种新途径。该类方法对目标函数性质要求低、容易实现、稳定性好,受到国内外学者的关注。
阿基米德优化算法(Archimedes Optimization Algorithm,AOA)是2020 年由Hashim 等[14]提出的一种新型启发式智能优化算法。该算法灵感来源于浸入流体中的物体与物体所受浮力的关系,个体通过不断调整自身密度和体积,使物体达到平衡状态,其中调整的过程即是种群寻优过程,达到平衡状态的个体即是全局最优解。相较于其他算法,AOA 局部搜索能力强、收敛速度快,但是仍存在很多不足:首先在迭代中后期算法不断围绕着全局最优位置的寻优方式,导致算法容易陷入局部最优,且全局搜索能力差;其次在搜索过程中,算法很难从个体信息上获取收益。
针对上述存在问题,本文提出了一种多策略阿基米德优化算法(Multi-Strategy improved AOA,MSAOA)。首先,利用变区间初始化策略来过滤搜索空间中冗余信息,以保证初始解的质量;其次,提出黄金莱维引导机制,扩大个体在迭代后期的搜索范围,以提高算法跳出局部最优的能力;最后,根据个体自身适应度值动态调整搜寻半径,在密度下降因子中引入自适应波长算子,提高AOA 的收敛速度。20 个经典测试函数和Wilcoxon 秩和检验测试的实验结果表明,所提算法性能优于原始算法,并通过4 个机械设计实例证实了所提算法可行性和有效性。
本文主要工作包括以下3 点:
1)提出了变区间初始化策略,提取和过滤搜索空间中的有用信息以保证初始种群向全局最优解靠近。
2)提出了黄金莱维引导机制,有效提高了种群多样性,增强了算法跳出局部的能力。
3)提出了自适应波长算子,并将其融入密度因子中,有效增强了个体的学习效率,以提高算法的寻优精度。
1 阿基米德优化算法
阿基米德优化算法(AOA)是一种基于种群的优化算法,设计灵感来自阿基米德定理。该原理指出,当物体完全或部分浸入流体中时,流体给物体施加的浮力大小与排出液体的质量(体积)成正比[15]:若物体受到的浮力等于排出液体质量时,视为该物体处于平衡状态,如式(1)所示。假设许多物体浸没在同一种流体中。每个物体都试图达到平衡状态。浸没的物体有不同的密度p和体积v,从而导致不同的加速度a。

其中:b 表示为流体,o 表示为物体个体。根据式(1)可将物体的加速度公式表示为式(2):

假如物体o 与另一个邻近物体r 的碰撞,导致当前物体的平衡状态将受到邻近物体的影响,则当前物体的平衡状态将为:

与其他的元启发式算法一样,AOA 以随机初始化物体的密度、体积和加速度开始搜索。在评估了初始种群的适应度后,AOA 进行迭代更新,直到终止条件满足。在每次迭代中,AOA 会根据个体与其他邻近个体是否发生碰撞选择位置方式,并更新个体自身属性。更新后的密度、体积、加速度决定了下一代个体的新位置。以下是AOA 步骤的详细数学表达式。
在初始化阶段,AOA 会随机初始化每个对象的体积(vol)、密度(den)、加速度(acc)。在此过程中,AOA 将评估初始种群,选取当前最优个体(xbest)、最优个体的密度(denbest)、体积(volbest)、加速度(accbest),用于其他个体密度、体积和加速度的更新。

式中:和为在t代中第i个和i+1 个体的密度和为在第t代中第i个和i+1 个个体的体积;rand∈(0,1)的随机数。
根据浸透在液体中的物体是否发生碰撞,AOA 将其分为全局探索和局部搜索阶段。若未发生碰撞,AOA 进行全局探索阶段;反之,进行局部开发阶段。通过设置迁移算子(Transfer Factor,TF),用于对两个阶段的切换,其定义如下:

式中:t和tmax分别表示当前迭代次数和最大迭代次数。
不同阶段对应不同加速度更新公式。当TF≤0.5,AOA进行全局搜索,个体的加速度进行更新方式为式(6):
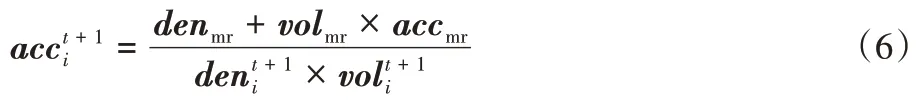
当TF>0.5,AOA 进行局部开发。个体的加速度进行更新方式为式(7):

为了规范个体的更新步长范围,AOA 将对个体的加速度进行归一化操作,如式(8)所示:
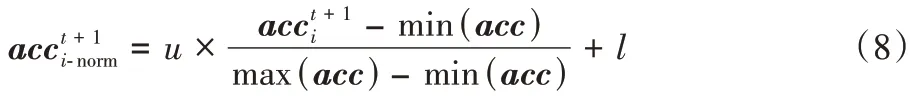
在全局搜索阶段,个体位置根据式(9)进行位置更新:

在局部开发阶段,个体位置根据式(11)进行位置更新:

式中:C2为固定常数;F为方向因子,用于决定迭代的位置更新方向,其定义为:

其 中:P=2rand-C4,C4为固定常 数;T=C3×TF,且T∈[0.3C3,1],C3为固定常数。
2 多策略阿基米德优化算法
2.1 变区间初始化策略
初始化种群的好坏一定程度上决定了算法的性能,初始种群在解空间中的细微不同,都可能影响算法进化方向。AOA 的初始种群在搜索空间中随机产生,导致初始种群分布不均匀,搜索范围有限。为了解决以上问题,获得好的初始种群,本文利用变区间初始化策略来提取搜索空间中有用信息以保证种群向全局最优解靠近。
对于优化问题:
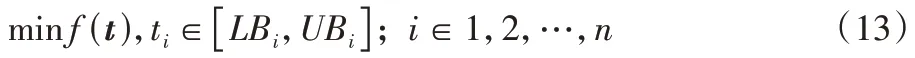
式中:LB(Lower Bound)表示搜索空间中的搜索下限;UB(Upper Bound)表示搜索空间中的搜索上限。变区间初始化策略对就是通过不断缩短[LB,UB],将初始种群逼近到式(13)中近似最优解的附近。
首先在中间取一个中点l。

生成两个个体:

式中a和b分别为:

计算f(x1)和f(x2)并比较它们大小,若f(x1)>f(x2),则有x*∈[l,UB],从而将潜在的最优解位置收缩到[l,UB]内;然后依次迭代,不断缩短搜索区间,并将搜索空间[LB,UB]分割成n-1 个子区间,把初始种群聚集到问题(13)的最优解附近。具体步骤参见算法1。
算法1 变区间初始化策略伪代码。

2.2 黄金莱维引导机制
在AOA 中,当迁移算子TF<0.5 时,AOA 进入全局开发阶段。由迁移算子定义可知TF∈(0.36,1],并且迁移算子会随迭代次数线性增长。该现象导致绝大部分迭代围绕着最优个体进行位置更新,引导个体朝向最优个体方向移动;然而当最优个体陷入局部最优时,很容易导致算法出现搜索停止的现象。为了加强AOA 跳出局部最优的能力,本文提出黄金莱维引导机制。
在凸优化理论中,AOA 收敛的关键之一是其步长应当满足适定性[16],即:步长较大会使得算法搜索精度低且收敛后期出现震荡现象;步长较小会导致搜索速度低,且不易跳出局部最优。莱维步长[17]是一种服从莱维分布的随机游动,其短距离与较长距离步长相间的特性,使得在未知范围内搜索时,能够达到更大范围,从而有助于算法跳出局部最优。步长s的计算公式为:

其中μ和ν服从正态分布:μ~N(0,σ2μ),ν~N(0,σ2ν)。
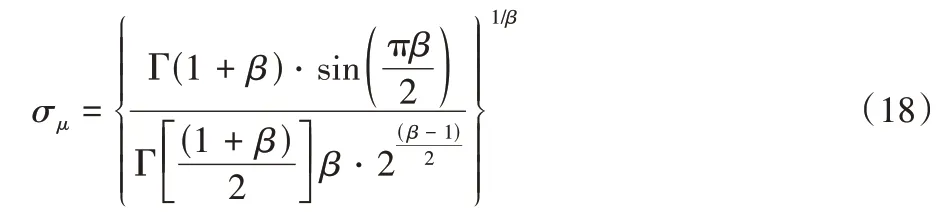
式中:σν通常取1;Γ(β)是Gamma 函数。根据文献[18]可知,β取值影响莱维飞行步长轨迹,β取值越大,局部开发能力越强。
其次,本文引入正弦函数与单位圆之间的关系[19],使得种群能遍历正弦函数上的所有点,即单位圆上的所有点。个体位置更新公式为:

式中:R1∈[0,2π]的随机数,R1和莱维步长s共同决定搜索半径;R2∈[0,π]的随机数,决定个体的位置更新方向;θ1和θ2是引入的黄金分割系数τ,其目的是缩小搜索空间,使得算法在每次迭代都会对能产生优秀解的区域进行充分搜索,从而加快了算法收敛速度。公式中具体参数表达式如下所示:
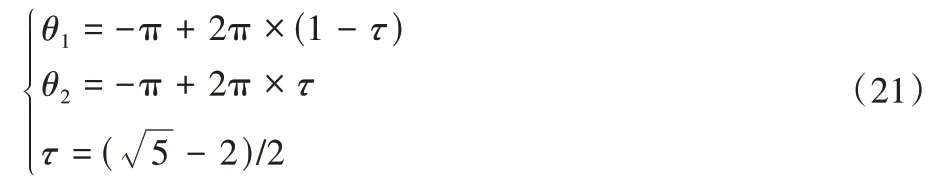
最后,虽然对目标个体使用黄金莱维引导机制,能让算法跳出局部最优,但并不能保证新的个体位置优于原目标个体位置,因此在引导机制后加入贪婪机制,通过比较个体位置更新前后个体适应度后再决定是否更新目标位置,以保留适应度较好的个体。贪婪机制具体操作表达式如下:

2.3 自适应波长算子
受到浸泡在液体中运动物体会导致水平面发生波动现象启发,本文提出了自适应波长算子:达到自身平衡(适应度较好)的个体,引起波动较小,从而具有较长的波长;还远未达到自身平衡(适应度较差)的个体运动会引起的较大波动,从而具有较短的波长。
在AOA 中,由于缺乏多样性的操作,当AOA 进化到一定的程度时,导致AOA 很难从自身适应度获取收益。因此结合浸泡在液体中运动物体的物理现象,本文提出自适应波长算子增强个体学习效率,提高算法寻优精度。

式中:λi表示第i个体运动引起的波长系数;f(Xi)表示当前迭代中第i个个体的适应度值;fmin和fmax分别表示当前迭代中最优适应度值和最差适应度值;α为衰减因子,ε为一个非常小的有理数,以防止分母为0 的情况。最后将自适应波长系数融合到密度因子,得到新密度因子更新公式为:
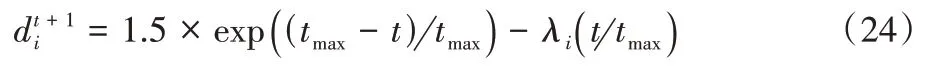
式中表示在t+1 代中第i个个体的密度因子。新的密度因子的大小会根据个体自身适应度动态变化:适应度接近最优适应度的个体,AOA 保持原来的密度因子的性质;而适应度较差的个体,密度因子接近最大值,使当前个体拥有较长的步长,快速向最优解靠近。
2.4 MSAOA时间复杂度
时间复杂度从理论上反映算法的收敛速度,在AOA 中,假设参数初始化(最大迭代次数为M,种群规模为n,空间维度d等参数),求解目标的适应度函数时间为f(d),由文献[14]可知,AOA 时间复杂度为O(M(n×f(d))),MSAOA 的时间复杂度与AOA 相同,分析如下。
初始化阶段 假设种群初始化参数比之前多x1,且变区间初始化策略时间复杂度O(n×f(d)),则MSAOA 种群初始阶段的时间复杂度为:

黄金莱维引导机制阶段 假设每一维度计算levy(λ)需要的时间为x2;生成随机数需要的时间为x3;根据式(19)需要的时间复杂度为O(2f(d)),则该策略需要的时间复杂度为:

引入自适应波长算子后的时间复杂度与AOA 基本相同。综上MSAOA 的时间复杂度为:

2.5 AOA的实现流程
本文所提算法MSAOA 的流程如图1 所示。
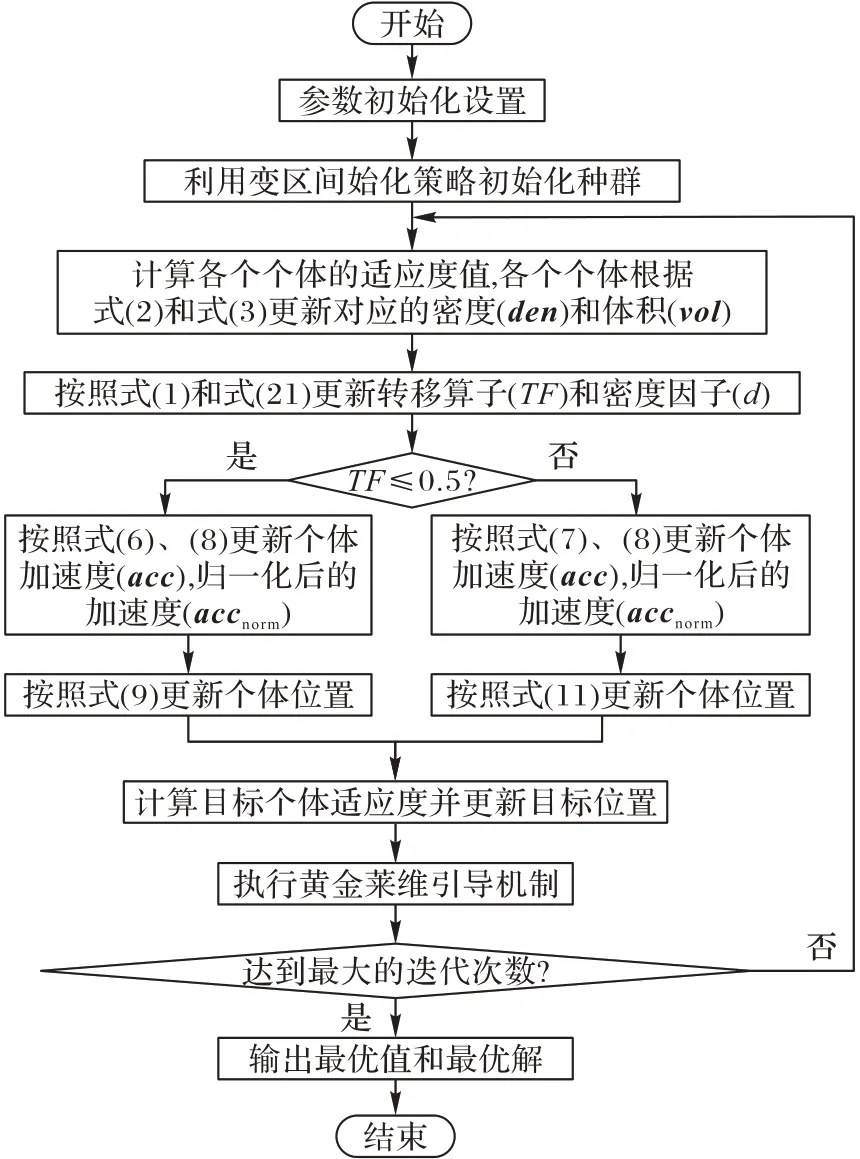
图1 MSAOA流程Fig.1 Flowchart of MSAOA
3 数值实验与结果分析
为了全面验证本文改进策略的有效性和鲁棒性,以及改进后算法的性能。本文验证实验分为3 个部分进行。
1)将MSAOA 与不同改进策略进行对比,验证改进策略的有效性;
2)将MSAOA 与其他群智能算法进行对比实验,再次验证MSAOA 的有效性;
3)通过Wilcoxon 秩和检验验证本文算法与其他对比算法之间的差异显著性。
实验引入20 个基准函数,分为3 类:第1 类为单峰基准测试函数,表1 中F1~F7 所示;第2 类为多峰基准测试函数,如表1 中的F8~F14 所示;第3 类为固定维度的多峰基准测试函数,如表1 中的F15~F20 所示。

表1 基准测试函数Tab.1 Benchmark test functions
算法的基本参数:种群规模为30,最大迭代次数为1 000,算法内参数如表2 所示。

表2 算法内参数Tab.2 Parameters in algorithms
3.1 与不同的改进策略对比
为了验证本文所提算法和每个改进点的效果,将多策略阿基米德优化算法(MSAOA)与阿基米德优化算法(AOA)、仅加入变区间初始化策略的阿基米德优化算法(AOA1)、仅加入自适应波长算子的阿基米德优化算法(AOA2)以及仅加入黄金莱维飞行引导机制的阿基米德优化算法(AOA3),同时在20 个经典基准测试函数下对比实验,进而客观地反映算法改进的有效性。
首先,为了体现实验的准确性能,图2 所示的6 个测试函数运行30 次的平均收敛曲线,其中纵坐标取10 为底的对数。通常采用单峰值函数(F1、F3、F6)来评价算法的开发能力,多峰值函数(F8、F10、F11)来评价算法的全局探索能力。由于加入黄金莱维引导机制,AOA 更容易跳出局部最优,所以MSAOA 的收敛速度和收敛精度上都优于其他算法,进而验证了改进策略的有效性。

图2 基准函数的平均收敛曲线Fig.2 Average convergence curves of benchmark functions
其次,表3 中最优值和标准差分别反映算法的寻优能力以及稳定性和鲁棒性。
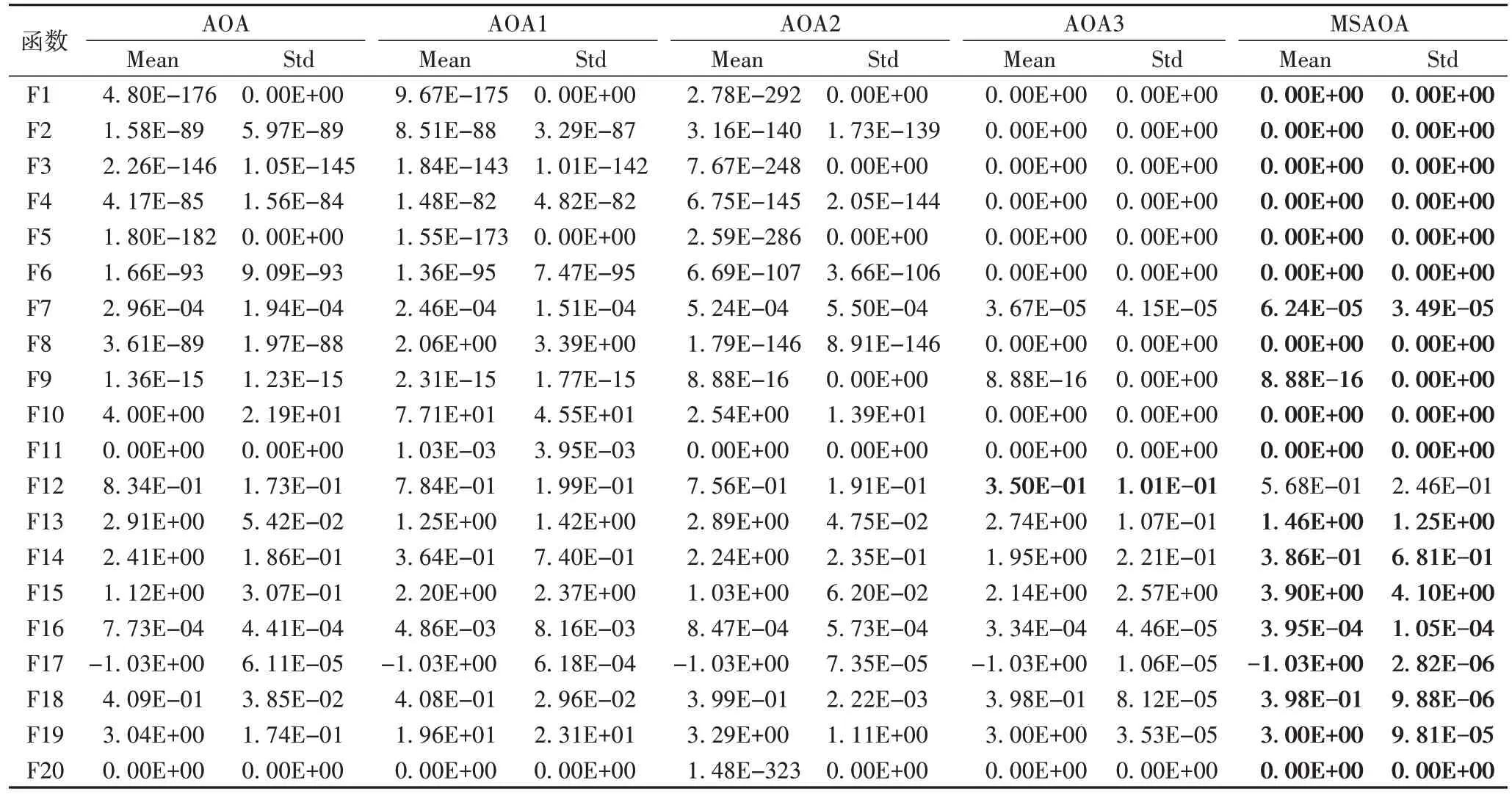
表3 基准测试函数上的测试结果Tab.3 Test results on benchmark test functions
从表3 纵向来看,在除去F12 外的单峰值函数,MSAOA均能找到理论最优值,且标准差最小。对于函数F7,MSAOA虽然没有达到理论最优值,但是MSAOA 的性能指标均优于其他算法。对于7 个多峰值函数,算法的求解精度相较于单峰值函数有所下降。MSAOA 在求解多峰值函数时,其中F8、F10、F11 达到理论最优值,且稳定性最好。对于其余多峰值函数,MSAOA 寻优精度以及稳定性上都优于AOA,客观说明MSAOA 能有效帮助算法跳出局部最优,拥有更强的全局搜索能力。对于固定维度函数,MSAOA 的平均值更接近理论最优值,同时MSAOA 的标准差明显优于AOA。纵向来说,3个改进策略对算法性能都有一定程度上的提升,其中仅加入黄金莱维飞行策略的阿基米德优化算法(AOA3)表现最为突出,引入自适应波长算子的阿基米德优化算法(AOA2)其次,结合变区间初始化策略的阿基米德优化算法(AOA1)次之。综合MSAOA 在表3、4 以及图2 上的表现,证明MSAOA 在多种基准函数上的求解效果,具有较强的寻优能力。
3.2 与其他群智能算法进行比较
将MSAOA 与粒子群优化(Particle Swarm Optimization,PSO)算法、灰狼优化算法(Grey Wolf Optimizer,GWO)、正余弦算法(Sine Cosine Algorithm,SCA)和均衡器算法(Equilibrium Optimizer,EO)进行性能比较,结果如表4 所示。对该五种算法在最大迭代次数为500、空间维度为100、种群规模为30 条件下进行仿真实验。由表4 可知,MSAOA在单峰基准函数的表现均优于其他算法,达到了显著的优化效果。在多峰函数中,对于寻优难度较大的F12,MSAOA 稳定性不如最新的均衡器算法(EO);然而,对于具有许多局部极小值点的F10 以及多模态函数F13,均达到了一定数量级的优化效果,并且在具有强烈震荡的复杂多模态函数F9 和F11 中,均取得理论最优值。最后在固定维度函数中,F17~F19 优化效果稍逊于均衡器算法(EO)。MSAOA 对于其他的固定维度测试函数上的优化效果仍然相对较好。
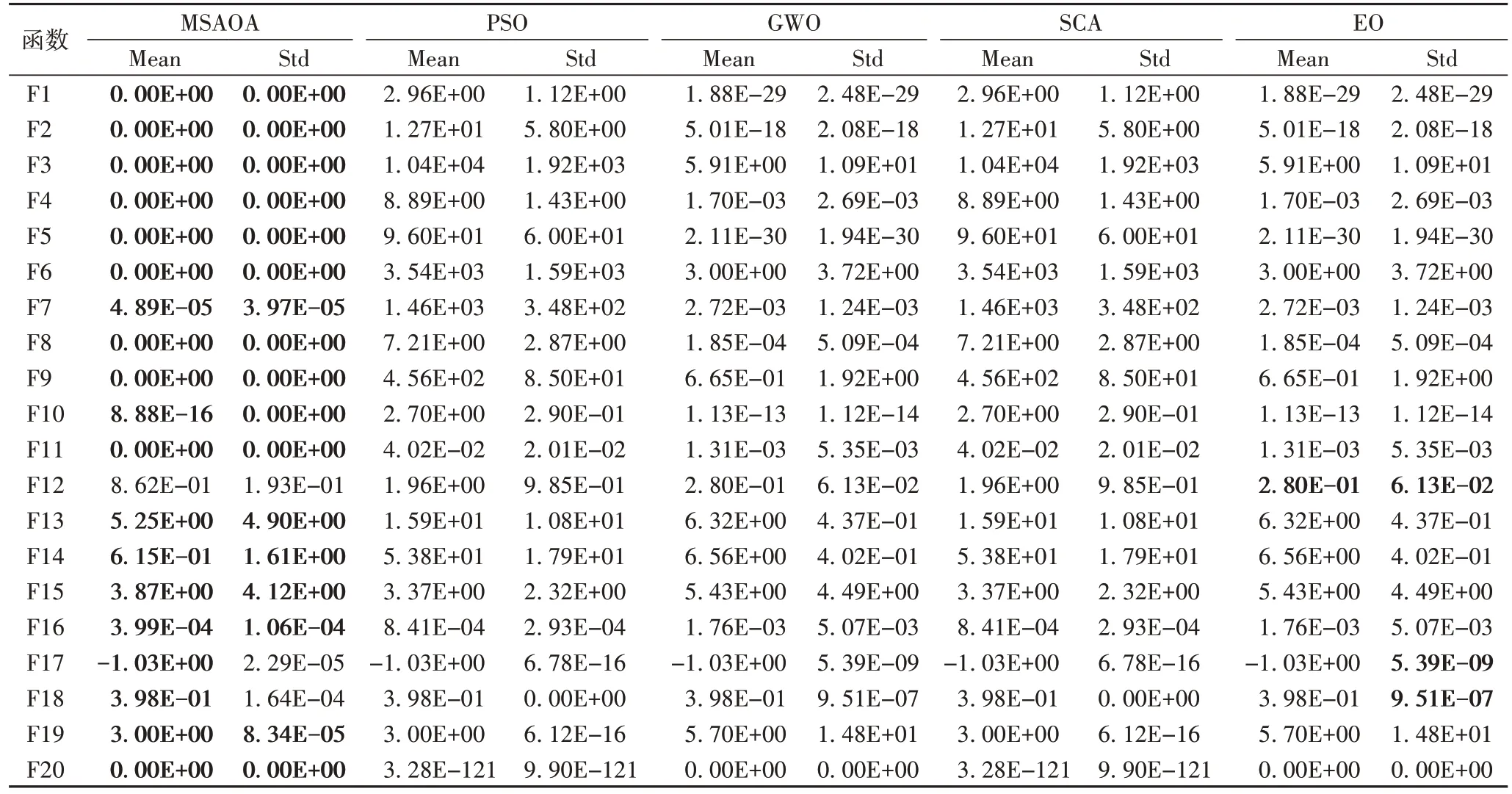
表4 所提算法与四种群智能算法结果比较Tab.4 Comparison of results of the proposed algorithm and four swarm intelligence algorithms
综上所述,本文提出多策略改进的阿基米德优化算法求解精度高、鲁棒性强和收敛较快,取得了相对较好的优化效果,提高了原始阿基米德优化算法的优化效率。
3.3 Wilcoxon秩和检验
本文采用Wilcoxon 秩和检验验证MSAOA 与其他算法的显著性差异。每次运行结果在p=5%的显著性水平下,当p值小于5%时,拒绝H0 假设,说明两种算法的差异性显著,否则就是接受H0 假设,说明两种算法在整体上是相同的。由于算法不能和自身比较,所以表5 中的标记为“NaN”表不适用,无法进行显著判断;“R”为显著性判断结果;“+”“-”“=”分别表示MSAOA 的性能优于、劣于和相当于对比算法的次数。从表5 中可以观察到大部分的p值是小于5%,因此表明该算法的性能在统计上是显著的,从而表明MSAOA 比其他算法拥有更好的优越性。

表5 基准函数上Wilcoxon 秩和检验p值Tab.5 p-values for Wilcoxon rank-sum test on benchmark functions
4 机械优化实例及结果分析
优化设计是20世纪60年代发展起来的一门新学科与设计方法。在实际机械设计中,某一类具体的实际问题都有其特定应用场合,表现出其特点以及复杂性。绝大多数机械问题与数学模型有着紧密联系,其中设计变量的选择、目标函数以及约束条件的确定是构造优化设计数学模型的主要步骤。该类问题的数学模型一般可以描述为如下带约束优化问题[20]:

在机械优化设计中,常常会遇到这一类数值优化问题。因此本文将提出的MSAOA 用于求解机械优化设计问题上,以验证MSAOA 在工程应用中的有效性和可行性。选取焊接梁的设计问题[21]、压缩弹簧的设计问题[22]、压力管道设计问题[23]和悬臂梁设计问题[24]作为工程算例进行分析。
为了体现比较的公平性,MSAOA 与粒子群优化(PSO)算法、引力搜索算法(Gravitational Search Algorithm,GSA)、生物地理学优化(Biogeography-Based Optimization,BBO)算法、差分进化(Differential Evolutionary,DE)算法、蚁群优化(Ant Colony Optimization,ACO)算法、樽海鞘群算法(Salp Swarm Algorithm,SSA)、正余弦优化算法(SCA)、AOA 进行对比实验时,各算法外基本参数设置相同,种群的规模N=30 和最大迭代次数M=1 000,独立运行30 次。
4.1 焊接梁设计问题
该问题以如图3 所示的焊接梁为研究对象,优化目标是使制造总成本最低。

图3 焊接梁设计问题Fig.3 Welded beam design problem
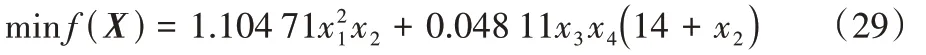
该问题共包含4个决策变量:焊缝宽度h、长度l、横梁宽度d、厚度b,分别表示为x1、x2、x3、x4;包含7 个约束条件如式(30)所示:剪切应力τ、横梁弯曲应力σ、屈曲载荷Pc、横梁挠度δ以及各设计变量之间尺寸约束,具体数学约束方程表示如下:


MSAOA 与其他算法的实验结果如表6 所示。从表6 中可知,MSAOA 对该问题的优化效果要优于其他的8种算法。

表6 九种不同算法求解焊接梁设计问题的对比Tab.6 Comparison of 9 different algorithms for solving welded beam design problem
4.2 压缩弹簧设计问题
该问题以如图4 所示的压缩弹簧为研究对象,优化目标是在受到最小偏差(g1)、剪切应力(g2)、冲击频率(g3)、外径限制(g4)和设计变量的条件下,尽可能减少弹簧重量。

图4 压缩弹簧设计问题Fig.4 Compression spring design problem

该问题共包含3个决策变量,分别是线径d(x1)、平均线圈直径D(x2)及有效线圈数P(x3)。式(36)为不等式约束条件:
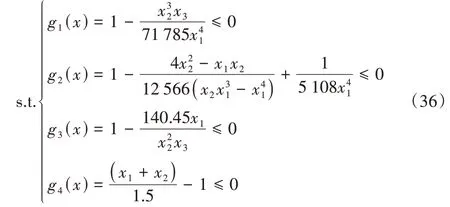
其中:0.05 ≤x1≤2.00,0.25 ≤x2≤1.30,2.00 ≤x3≤15.0。
MSAOA 与其他算法的实验结果如表7 所示。从表7 中可知,MSAOA 对该问题的平均值和标准差最小,优化效果优于其他8 种算法。

表7 九种算法求解压缩弹簧设计问题的对比Tab.7 Comparison of 9 algorithms for solving compression spring design problem
4.3 压力管道设计问题
根据压力管道平面结构图5,该问题设计目标为最小化费用总成本。

图5 压力管道设计问题Fig.5 Pressure piping design problem

式中:x1(壳体厚度Ts)、x2(头部厚度Th)、x3(内半径R)、x4(圆柱体长度L)。该问题的约束方程如下所示:

对获取最佳解决方案的不同算法进行比较,从表8 可知,MSAOA 与其他算法相比,平均值优于其他8 种算法,其次标准差远小于其他8 种算法,表现出极强的稳定性。
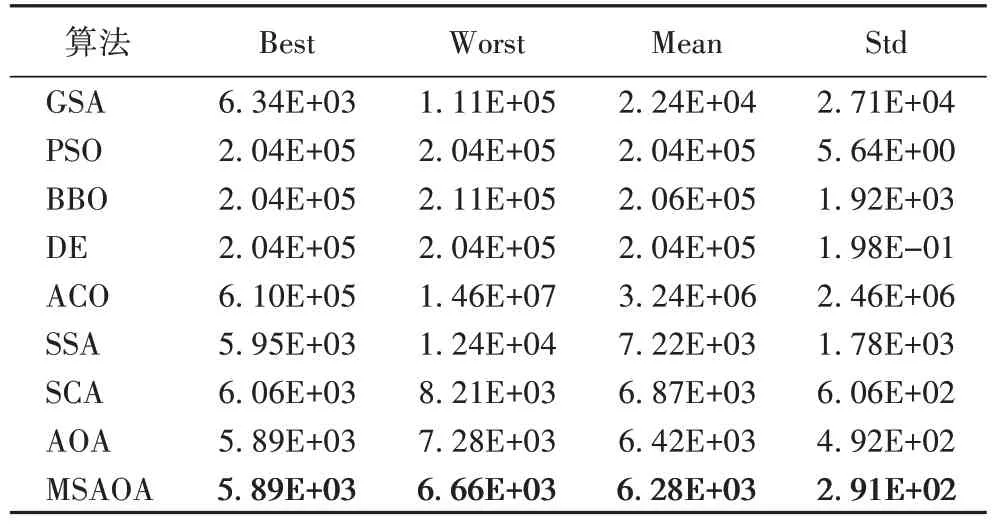
表8 九种算法求解压力管道设计问题的对比Tab.8 Comparison of 9 algorithms for solving pressure piping design problem
4.4 悬臂梁设计问题
根据悬臂梁平面结构(图6),该问题受到不同单元梁高度或宽度的约束,设计目标为尽可能减小悬臂梁矩形截面的重量。其数学模型如下:
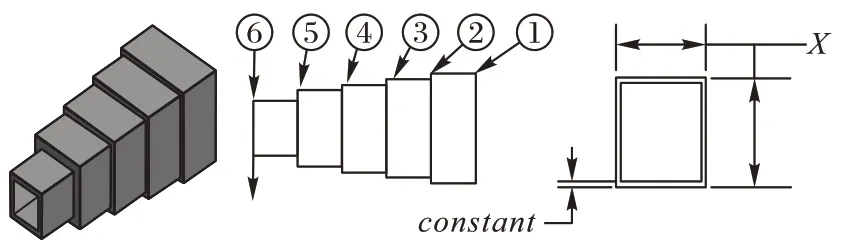
图6 悬臂梁设计问题Fig.6 Cantilever beam design problem
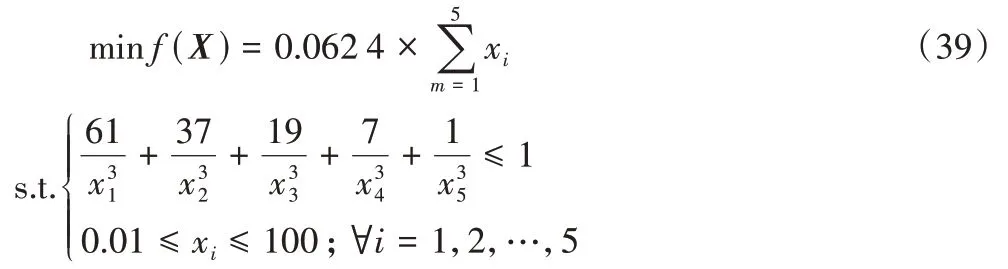
式中:f(x)为最小化悬臂梁矩形截面的重量,设计变量xi表示5 个不同单元梁的高度或宽度。
表9 是MSAOA 与其他算法获取最优解的对比实验结果。

表9 九种算法求解悬臂梁设计问题的对比Tab.9 Comparison of 9 algorithms for cantilever beam design problem
从表9 中可以明显地看出,MSAOA 获取的平均值和标准差都小于对比算法,具有较高的收敛精度和较强的鲁棒性。
5 结语
为了解决AOA 存在的问题,本文提出了一种多策略阿基米德优化算法(MSAOA)。首先,提出了变区间初始化策略,为算法的迭代奠定良好基础;其次,提出了黄金莱维引导机制,加强了AOA 跳出局部最优的能力;最后,提出自适应波长算子,提高个体学习效率。将本文算法与主流算法在20 个基准测试函数以及部分CEC2014 函数上进行比较,使用数值分析、收敛性分析、Wilcoxon 秩和检验对实验结果进行评估。评估结果表明,本文算法有效,具有更高的寻优精度和收敛速度,与对比算法差异性显著;将本文算法应用于4 个机械设计实例中,再次验证了MSAOA 的有效性和优越性。下一步工作可围绕着两个方面进行:将本文算法改进思想应用在其他元启发式算法中,验证本文改进策略的泛化能力以及有效性;将MSAOA 应用在机器学习参数优化和智能电网参数优化当中,为解决参数优化问题提供一个新途径。
