基于CNN-BiGRU的水电机组振动趋势预测
2022-09-24邓玉敏张雪桂严耀亮李超顺
邓玉敏,张雪桂,马 历,严耀亮,李超顺
(1.中国长江三峡集团有限公司,武汉 430000;2.华中科技大学土木与水利工程学院,武汉 430074)
0 引 言
水电机组作为水力发电的关键设备,机组的安全稳定运行至关重要,其运行状态信息通常表征在机组的一系列监测物理量中。因此可以通过采集到的监测数据进行分析,并通过预测模型对设备在未来某一时期状态趋势进行预测[1]。
水电机组的状态信息蕴藏于振动信号中。在工程实际中,振动摆度信号蕴含了约80%的机组性能状态信息,通过分析振动信号可以获取机组的健康状态[2,3]。水电机组振动趋势预测是一个非线性非平稳的序列预测问题[4],针对状态趋势的预测,例如,文献[5]通过对机组水导轴承X 方向建立了BP 神经网络预测模型进行预测,但此方法需要大量长时间的机组振动数据做基础;文献[6]通过支持向量回归机(SVR)的预测模型完成对上机架振动、水导摆度历史数据进行趋势预测,但此方法容易出现“过学习”现象;文献[7]采用时间序列模型预测法中的自回归滑动平均(ARMA)模型,分别预测抽水和发电工况下的机组上导轴承和上机架的振动趋势,证明了时间序列预测法可实现不同机械设备的振动趋势的预测;文献[8]针对水电机组信号的复杂非平稳特性,提出了一种基于能量熵重构(EER)与支持向量回归(SVR)的混合预测模型,通过对信号的重构从而降低复杂度,最后得到最优SVR,提高了预测模型精度;文献[9]使用神经网络和支持向量机的预测方法,虽取得较好的效果,但对于水电机组这种非常复杂的系统进行神经网络训练时,因其系统复杂规模庞大,神经网络模型的学习训练需要较长的时间,降低了神经网络的实用性。
文献[10]采用WTD方法对振动信号数据进行降噪处理,再采用BiGRU 网络建立振动信号预测模型,完成振动信号的趋势预测;文献[11]针对水电机组的振动信号的非平稳性、非线性的特点,提出了基于VMD 的CNN-LSTM 混合神经网络的趋势预测方法,与传统神经网络相比,CNN 可以更好地提取数据内在特征,构建网络时所需参数更少,在保证精度的同时提高了计算速度。
为了进一步提高水电机组振动预测精度,针对目前单一模型难以获得最优预测结果的问题,提出了一种CNN-BiGRU 模型组合的水电机组振动预测方法,并构造出CNN-BiGRU 网络组合预测模型。利用CNN 提取数据局部特征,实现了对数据潜在特征关系的挖掘。又因水电机组振动信号在时间序列中存在联系,为完成时序信号的特征挖掘预测,故将CNN 网络和BiGRU 网络进行并行预测,通过多模型组合预测来避免单一模型难以获得最优结果的问题,从而提高水电机组振动预测精确度与可靠性。实验结果证明提出的模型有效的提高了预测精度,取得了较好的预测结果。
1 基础理论
1.1 一维卷积神经网络
CNN 是典型的多层前馈神经网络,常用于图像处理领域,因它可以避免层间因完全连接而造成的参数冗余,通过局部的连接方式,降低了训练的难度和对数据的依赖性。CNN 主要包含三种层:卷积层、池化层和全连接层。卷积层将特征向量经过卷积运算传递给池化层,池化层对数据进行降维处理,通过卷积层和池化层的交替使用能够有效的提取数据局部特征并降低局部特征维度,经过多个卷积层池化层交替运算,最终,将得到的高级特征信息通过全连接层输入下一层网络进行下一步预测。通常,CNN 在处理二维图像问题时需要三个维度的数据:宽度、高度和通道数。而一维CNN 可看作是输入数据高度为1时的特殊情境。一维卷积运算如式(1)所示:

1.2 门控循环单元
GRU 是一种特殊的RNN,与LSTM 相比,它具有快速收敛和参数更少的优点,在保证预测性能的前提下,简化了复杂的结构,提高了运算速度。因此,GRU 比LSTM 网络更简单、更有效。GRU结构如图1所示。

图1 GRU网络结构图Fig.1 GRU network structure diagram
设xt为输入,ht为隐藏层输出,则GRU计算流程如下式:

式中:rt为重置门;ht-1为前一时刻隐藏单元的输出;σ为sigmoid的激活函数;Wr、Ur、br、Wh、Uh、bh、Wz、Uz、bz分别为可训练的权重参数和偏置。
1.3 双向门控循环单元
BiGRU 是GRU的改进,基于正反2层GRU神经网络构造分别处理数据,即使用一个GRU 神经网络来计算过去的信息,并同时使用另一个相同且方向相反的GRU来计算未来的信息,通过前向与反向的GRU 单元学习历史与未来时刻对当前信息的影响。其结构如图2所示。

图2 BiGRU网络结构图Fig.2 BiGRU network structure diagram
2 CNN-BiGRU预测模型
CNN-BiGRU 组合预测模型网络结构见图3。本模型中保留了CNN 提取非线性特征能力并与BiGRU 处理长序列的数据挖掘能力相结合,从而避免有用信息丢失,发掘序列的长依赖性。

图3 基于CNN-BiGRU组合预测模型Fig.3 Based on the CNN-BiGRU combination prediction model
2.1 CNN模型设计
水电机组振动信号具有强烈的非线性,而CNN 具有强大的非线性特征获取能力,故由CNN 层提取相应特征进行学习预测。CNN 模型网络中选用两层重复卷积,目的是尽早提取到信号的高级特征,避免信号在通过池化层时失去重要特征;池化层选用最大池化操作,对卷积层所提取特征进行向下采样,从而精简模型参数;最后将数据输入全连接层,CNN 中全连接层的作用是把池化后的特征向量进行重新组装拟合,并通过激活函数增加模型的非线性能力,与其他激活函数相比,ReLU 输出的特征具有稀疏性,使得网络具有较好的泛化能力。此外,在输入大于0时,ReLU的导数恒为1,使得网络计算速度较快且不易出现梯度弥散。
2.2 BiGRU模型设计
水电机组振动信号机组振动信号本身具有时序关系,而Bi-GRU 在时序序列的预测中具有良好效果。BiGRU 网络中选用两层BiGRU 层,完成时序信息的有效提取,但当BiGRU 模型参数过多时,容易产生过拟合现象。为防止训练过度,BiGRU 层采Dropout 机制,随机丢弃一部分神经元节点使其暂时不参与模型训练,使得BiGRU 网络不会过度依赖部分特征提升模型的泛化能力。最后将处理后的数据输入BiGRU的全连接层。
2.3 全连接层设计
数据经过CNN 模型和BiGRU 模型分别处理后并行拼接作为全连接层输入,考虑到模型结构的非线性,构建了3 个Dense层,分别有32个16个和1个神经元,完成模型的输出。
2.4 评价指标
将测试集输入数据矩阵化处理后依次输入训练好的网络中,将网络的输出与测试集的输出数据进行比较,计算结果的平均绝对误差(Mean Absolute Error,MAE),平均绝对百分误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE),计算公式如下所示:

式中:xi是真实值为模型输出值;n为序列的长度。
3 实例分析
3.1 数据的选取与处理
相关研究表明,波形的标准差或峰峰值可以较好的反应机组的状态[12-14],因此本实验中使用振动信号峰峰值作为实验数据。本实验以某电站3 号机组的上导X方向摆度与下导X方向摆度数据峰峰值作为研究对象,实际生产中,机组振摆采样频率较高,短时间会产生大量高密度数据[15],为有效进行预测,为避免机组启停时刻的异常值影响,研究选取机组2019年3月2日0 时至2019年9月1日0 时发电稳态(机组开机后一小时,停机前10 min)采集到的监测数据,选取时间间隔为5 min 的数据,最终选取机组稳态峰峰值共5 080 条,实验中,选取前4 500条数据作为训练集,后580条数据作为测试集。
首先将数据进行划分为训练集和测试集,后对数据进行归一化处理,归一到区间[0,1]中,归一化公式:

式中:xmax,xmin分别为数据中的最大值和最小值。
3.2 训练方法优选
为保证模型的训练具有良好的精度与泛化能力,因此在网络训练中需要选取合适的参数,CNN-BiGRU 模型中的参数设置详情如下:
(1)损失函数。损失函数用于评价模型训练过程中真实值与预测值之间的差距,损失函数值越小,表示模型训练时的表现越好。常见的损失函数主要包括:MAE和MSE等。而MSE是常用于回归预测问题中的损失函数,因此,本文采用MSE作为CNN-BiGRU网络的损失函数。
(2)网络学习率与迭代次数。学习率控制了模型的训练步长,决定了模型能否收敛与收敛的速度。在CNN-BiGRU 网络中,通过试错法网络学习率为0.01,全连接层中dropout 值设置为0.2。
(3)优化算法。优化算法的正确使用可有效提升模型的训练速度和预测精度。目前应用较多的优化算法有Adam、RMSprop、SGD,本文分别使用3 种优化算法对CNN-BiGRU 模型进行150 次训练,实验结果如图4 所示。从图4 中可以看出Adam训练的网络效果最好,RMSprop 则相对滞后,SGD 的效果最差。因此最终本模型选用Adam作为模型优化器。
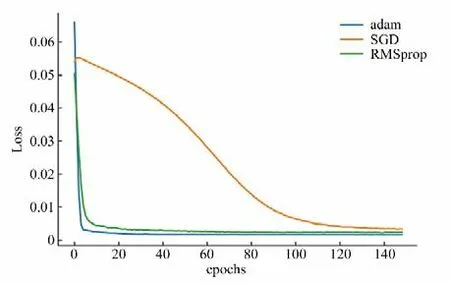
图4 优化算法对比Fig.4 Optimize algorithm comparison
3.3 实验结果对比
为验证所提方法的有效性,以上导摆度X向振动峰峰值数据分别多次训练和测试模型,将其与GRU 模型、BiGRU 模型、CNN-GRU 并行网络、CNN-LSTM 并行网络进行对比分析,结果如表1 所示。根据预测结果可知,所提组合模型效果最佳,而CNN-LSTM 网络效果最差。
从表1可以看出:

表1 上导摆度X向振动峰峰值预测结果对比Tab.1 The up-guided slew X is compared to the prediction results of vibration peaks and peaks
(1)所提组合模型相较于GRU、BiGRU 单一预测模型,MAE分别降低了53.09%、51.87%,MAPE 分别降低了52.83%、51.39%,RMSE 分别降低了64.28%、62.77%,可以看出当使用CNN 模块提取数据特征后,水电机组振动峰峰值预测精度大幅提升,这表明并联CNN 模块可有效提升水电机组振动信号的预测精度。
(2)所提组合模型相较于CNN-GRU、CNN-LSTM 组合预测模型,MAE分别降低了49.05%、56.86%,MAPE 分别降低了48.42%、56.22%,RMSE 分别降低56.76%、64.35%,这表明了采用BiGRU 同时学习未来和历史信息,可以增强模型的对时间序列的学习能力,使得预测的更加准确。
本实验所提模型与对比模型在相同工况下的上导摆度X方向上的测试结果如图5、6所示。可以看出对比模型预测结果整体趋势与实际值保持一致,但是局部误差较大。而CNN-BiGRU 模型预测结果可表示出真实值的整体趋势与局部特征的变化,除个别极值点外,模型的预测值与实际值基本吻合,可最大程度的反映水电机组振动的波动情况。

图5 上导摆度X方向本模型与单一模型预测对比图Fig.5 The up-guided slew X direction of this model is compared with the single model prediction
为进一步证明所提模型的有效性,将各模型应用于下导摆度X向振动峰峰值预测。图7、8展示了所提模型与对比模型在相同工况下的下导摆度X方向上的多次测试结果。表2展示了不同模型对下导摆度X方向的预测结果,可以看出CNN-BiGRU 模型相较于其他模型预测精度更高,误差更小。证明了该模型在机组振动预测方向上的优越性。

表2 下导摆度X向振动峰峰值预测结果对比Tab.2 The hemline X contrasts with the prediction results of vibration peaks and peaks

图6 上导摆度X方向与组合模型预测对比图Fig.6 The up-guided slew X direction of this model is compared with the combined model prediction

图7 下导摆度X方向本模型与单一模型预测对比Fig.7 Hemline X direction This model compares with a single model prediction
4 结 语
针对水电机组振动信号非平稳和非线性问题,提出一种基于CNN-BiGRU 组合模型的水电机组振动预测方法,首先利用CNN 提取数据有效局部特征,再运用BiGRU 模型处理时序性特征数据,深度挖掘水电机组振动数据的非线性以及时序性特征。通过与传统预测模型进行对比,结果表明本文提出的混合模型有更高的预测精度,证明该模型可充分提取输入数据的特征并利用数据的时序性特征进行振动信号预测。

图8 下导摆度X方向与组合模型预测对比图Fig.8 Hemline X direction This model compares with the combined model prediction
