基于神经网络和智能优化算法的水电机组自适应PID控制

黄金龙，秦小元，沈博渊，夏 晨，陈金保，肖志怀

（1.向家坝水力发电厂，四川宜宾 644612；2.南京南瑞继保电气有限公司，南京 211101；3.武汉大学水力机械过渡过程教育部重点实验室，武汉 430072；4.武汉大学动力与机械学院，武汉 430072）

0 引 言

中国是水资源开发和利用大国，水电机组装机容量世界领先。近年来，随着金沙江、雅砻江等流域巨型水电站的相继建成和投入运行，我国电力系统中水力发电占比进一步提高，加之风、光等可再生能源在电网中的渗透率增加，调度部门对水电调节的灵活性和可靠性要求日益严格［1］。在电网的调节过程中，水电机组主要通过承担黑启动、冷热备用、调峰调频等关键任务来满足系统功率、频率和电压的稳定，保证电能质量。在水电占优电力系统中，低频振荡是重要的动稳定问题之一，与水电的负阻尼效应直接相关。大量研究表明，水轮机调速器控制参数设置不合理是造成此类现象的主要原因［2］。我国绝大多数电站的水轮机调速器根据不同的控制模式采用提前整定好的一组或几组控制参数，并且在机组运行过程中，这些控制参数的设定值保持不变。水电机组所具有的强非线性、非最小相位特性决定了系统在不同水头和负荷下的稳定性是不同的［3］。固定的PID 参数无法根据机组的运行工况进行适应性地调整，在某些工况下可能会出现调节品质恶化，甚至造成机组振荡、解列等严重问题。因此，水电机组的优化控制是提高调速器调节品质和电力系统稳定性的重要方式。

PID 控制策略具有结构简单、可靠性强，参数物理意义明确、调节方便等优点，在工业控制过程中得到了广泛应用［4］。但对于复杂的非线性系统，仅靠一组PID 参数难以满足多工况的控制要求。目前，水电机组的优化控制主要从PID 控制策略优化和先进控制算法两个方面开展研究［5］。在PID 控制策略优化方面，可以通过优化控制器结构或参数或借助智能算法辅助调节等方式提高PID 控制器的控制性能以及PID 参数对机组工况的自适应性［6，7］。高菘等人利用生物地理学优化算法对水电机组的PID 参数进行了优化，并通过对比试验验证了该算法在控制参数优化方面的优势［8］。Chen等人将分数阶PID控制器引入水轮机调节系统，并利用改进的引力搜索算法优化控制器参数，得到了满意的控制性能［9］。通过设计模糊系统以实时优化PID 参数，能够实现调速器控制参数的自适应调整［10-12］。在先进控制算法方面，滑模控制、预测控制、模糊控制、神经网络控制等在水电机组控制中的理论研究得到了较快发展，是最具潜力的几种先进控制算法［13-16］。吴道平等人设计了适用于非最小相位系统的水电机组改进滑模控制策略，并对滑模控制参数进行了优化，克服了传统滑模控制存在的假稳定现象［1］。Xiao和王涛等人分别设计了用于水电机组的神经网络控制器，提升了水电机组的控制性能［17，18］。Zheng 等人开发了基于树种算法的多模态预测控制算法，并在多种工况下证明了该控制器在机组电压和频率调节中的优异性能［19］。

虽然先进控制算法对水电机组的优异控制性能在仿真中得到了充分验证，但算法的复杂性和可靠性使得其距离实际应用还需时日，而在以模糊系统为代表的自适应PID控制中，知识的获取也需要专家经验的支持，增加了算法设计的难度。考虑到目前水轮机调速器仍以PID 控制为主，本文基于智能优化算法和神经网络，设计了一种易于实现的水电机组自适应PID 控制器。首先建立了水轮机的神经网络非线性模型。其次，对水轮机非线性模型进行局部线性化处理，得到不同工况下的水轮机传递系数，进而建立水轮机调节系统的分段线性模型。基于该分段线性模型，利用一种改进的粒子群算法和绝对误差时间积分目标函数，对不同工况下水轮机调节系统的PID 控制参数进行优化。最后以一系列参数优化结果作为学习样本分别得到反映三个PID参数与机组运行工况（导叶开度和工作水头）关系的神经网络，进而得到水电机组的自适应PID 控制器。为验证该控制器的性能，将其在不同工况下的控制性能与传统的定PID 控制进行对比。结果表明，本文设计的自适应PID 控制器具有良好的工况自适应性，在不同工况下均具有比定PID 控制更优异的调节性能。

1 水轮机调节系统数学模型

1.1 调速器模型

调速器是水电机组的核心控制设备，包含控制器和随动系统两个部分。其主要工作原理是通过接收电网频率波动信号调整导叶开度，使机组出力发生变化，进而保持电网的频率稳定和功率平衡。对于本文研究的水电机组，控制器采用并联PID 型控制策略，随动系统主要由比例阀、中间接力器、主配压阀和主接力器构成。调速器整体传递函数如式（1）所示［20］。

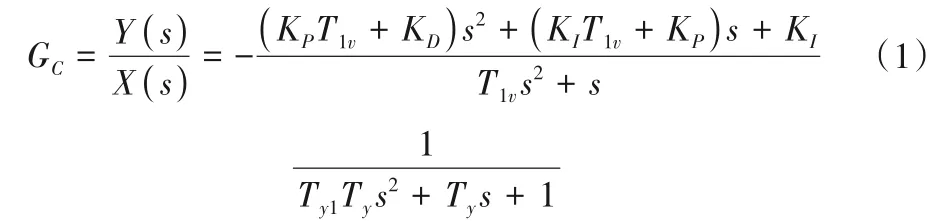
式中：KP、KI和KD分别为控制器的比例、微分和积分系数；T1v为微分环节时间常数；Ty1和Ty分别为中间接力器和主接力器反应时间常数；Y为导叶开度；X为机组转速。

1.2 发电机模型

发电机模型由运动方程和电磁方程组成。当考虑电气量暂态或次暂态过程时，需要使用三阶及以上高阶发电机模型。由于本文研究不涉及电力系统建模，仅考虑调速器的频率控制模式，因此负载可用常数表示，发电机及负载传递函数采用一阶惯性环节，如式（2）所示［20］。

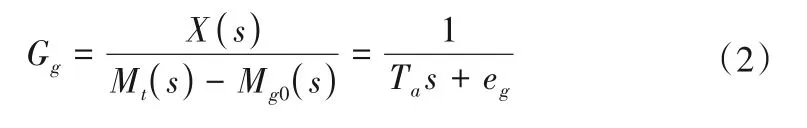
式中：Ta为机组惯性时间常数；eg为发电机负载自调节系数；Mt为水轮机力矩；Mg0为负载力矩。

1.3 水力系统模型

水电站水力系统自上而下一般包含水库、引水管道、调压室、水力机组、尾水隧洞等水力元件。根据压力管道的长度以及仿真工况，引水系统可采用不同的水击模型。在调节系统小波动条件下，当压力管道长度小于600～800 m 时，一般采用刚性水机模型，反之采用弹性水击模型；对于调节系统大波动过程，一般采用特征线法［21］。本文研究的机组压力管道长度较短，因此采用如式（3）所示的刚性水机模型［20］。

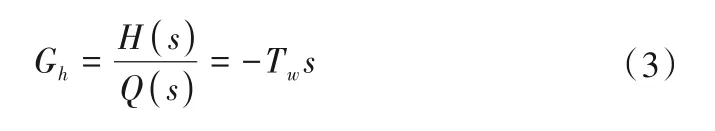
式中：Tw为水流惯性时间常数；H为水轮机水轮机工作水头；Q为水轮机过流量。

1.4 水轮机模型

水轮机模型分为线性模型和非线性模型，均可由模型试验得到。线性模型以传递系数表示，可用于调节系统小波动仿真；非线性模型一般利用插值、神经网络等方法对模型试验数据进行拟合，可用于调节系统大波动仿真。水轮机线性和非线性模型分别如式（4）和（5）所示［20］。

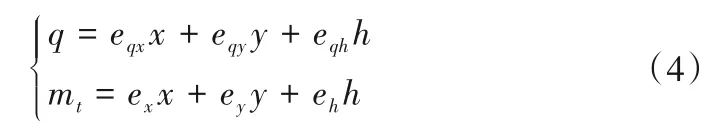
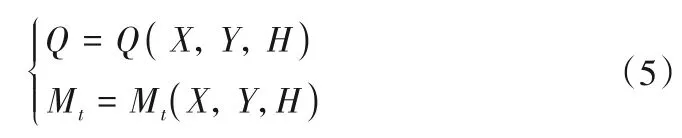
式中：eqx、eqy和eqh分别为水轮机流量对转速、导叶开度和水头的传递系数；ex、ey和eh分别为水轮机力矩对转速、导叶开度和水头的传递系数；Q为水轮机流量；Mt为水轮机力矩；q、mt、x、y和h分别表示水轮机流量、力矩、转速、开度和水头的偏差相对值。

联合各子系统的数学模型，可得到水轮机调节系统的分段线性化模型，如图1所示。在该模型中，水轮机的传递系数随工况发生变化，当指定某一特定工况时，可将水轮机非线性模型在该工况处线性展开，求得该工况下水轮机的传递系数。传递系数的计算方法除了传统方法之外，还可采用基于神经网络的求导方法，具体内容见文献［22］。

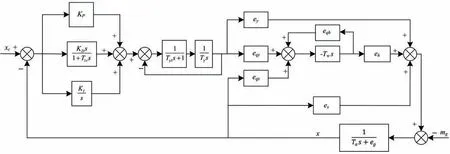
图1 水轮机调节系统的分段线性化模型Fig.1 Piecewise linearization model of hydraulic turbine governing system

2 自适应PID控制器的设计

为设计适应于水轮机工况变化的PID 控制器，首先需要获取机组运行工况与最优PID 参数的对应关系，其次利用传统数学或人工智能方法构建映射这种复杂关系的非线性函数。基于上述思想，本文设计了基于智能优化算法和神经网络的水电机组自适应PID 控制器，主要步骤如下，相应的流程图如图2所示。

图2 自适应PID控制器的设计流程图Fig.2 Design flow chart of adaptive PID controller

（1）基于模型综合特性曲线、飞逸特性曲线和其他边界条件构成的学习样本建立水轮机的神经网络模型，详细建模方法见文献［22］。

（2）将机组整个运行工况按导叶开度和水头均匀地划分为若干工况点，利用文献［22］提出的神经网络求导法计算不同工况点处的水轮机传递系数，得到全工况下水电机组分段线性模型。这样做的目的是降低模型的复杂性，节约计算时间。

（3）基于系统分段线性模型，以时间误差积分（ITAE）指标为目标函数，利用一种性能优异的自适应模糊粒子群算法［23］优化不同工况点处的PID 控制参数，得到若干对应不同工况的最优PID参数。

（4）将若干工况点及其对应的最优PID参数作为学习样本，以标准BP 神经网络作为拟合工具，通过一定时间的训练得到3个反映不同的最优PID 参数与工况关系的神经网络，分别记为KP神经网络、KI神经网络和KD神经网络。它们的输入均为导叶开度和水头。

（5）将构建的3 个用于PID 参数实时调整的神经网络嵌入传统的PID 控制器中，得到适应于水轮机工况变化自适应PID控制器。

通过以上步骤得到的自适应控制器的结构框图如图3 所示。可以看出，相比传统的PID 控制器，该控制器的PID 参数可通过输入的导叶开度和水头，经过3 个不同的神经网络计算求得，是一种在线PID 调整方法。由于神经网络的训练数据是各个工况下的最优PID 参数，因此能够保证PID 控制器在不同工况下都具有良好的控制效果。

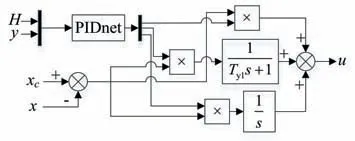
图3 水电机组自适应PID控制器Fig.3 Adaptive PID controller of hydropower unit

3 仿真验证和结果分析

本文以某电站为例，验证本文提出的自适应PID 控制器在大型混流式水电机组上的应用效果。机组的基本参数为：额定功率812 WM，额定流量890 m3/s，额定转速75.0 r/min，额定水头100 m，水头变化范围为86.1～114.2 m，带负荷条件下开度变化范围为20%～100%。模型的基本参数为：T1d=0.1，Ty1=0.041，Ty=0.46，Tw=1.39，Ta=9.3，eg=0.086。根据水头和导叶开度的变化范围，导叶开度每隔10%作为一个工况点，水头每隔2 m作为一个工况点，因此整个运行工况将划分为135 个工况点。根据每个工况点对应的开度和水头，利用水轮机神经网络模型可以得到相应的水轮机传递系数和水轮机调节系统分段线性模型。对各个分段线性模型的PID 控制参数按照第3 部分中的步骤（3）进行优化，得到一系列最优PID 控制参数，如图4-6 中的灰色圆点所示。利用不同控制参数和工况之间的关系样本训练BP 神经网络。为保证良好的训练效果，对于每个控制参数，将全部样本分为训练样本、验证样本和测试样本，占比分别为80%、10%和10%。训练方法采用兼具梯度下降法和高斯牛顿法优点的LM 算法。最大迭代次数为1 000。经过反复比较，神经网络采用1 个隐含层的3 层架构，隐含层的神经元数目对于KP、KI和KD分别为6、5和5。训练得到的与不同控制参数有关的3 个神经网络分别如图4-6 中的曲面所示。训练过程MSE 变化曲线以及最终误差如图7所示。由图4-6可以看出，最优PID参数样本点基本都落在了神经网络的拟合曲面上，表明神经网络的训练误差较小，拟合精度较高，能够很好地表征最优控制参数随工况的变化情况。由图7可以看出：KP、KI和KD神经网络训练过程中的MSE 均能达到稳定状态，表明训练过程中无明显的过拟合现象；网络预测实际误差较小，其输出与样本贴合度高。

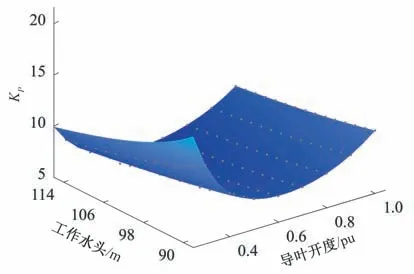
图4 最优KP及其神经网络拟合曲面Fig.4 Optimal KP and its neural network fitting surface

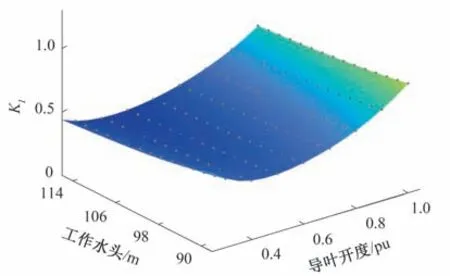
图5 最优KI及其神经网络拟合曲面Fig.5 Optimal KI and its neural network fitting surface

图6 最优KD及其神经网络拟合曲面Fig.6 Optimal KD and its neural network fitting surface

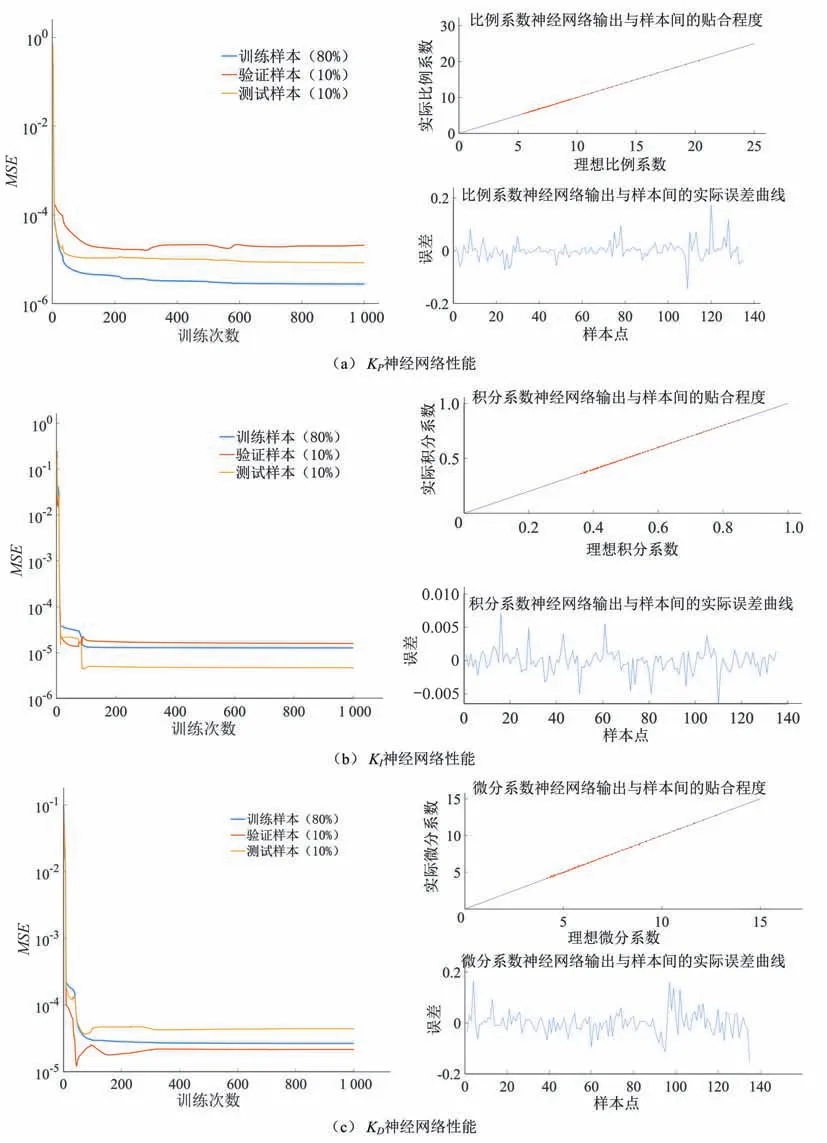
图7 KP、KI和KD神经网络训练过程MSE变化曲线以及最终误差Fig.7 MSE variation curve and final error of KP、KI and KD in the training process of neural network

最后，选择4个不同的工况，用带有水轮机神经网络模型的水轮机调节系统模型进行仿真测试，验证所提出的自适应PID控制器相较传统的定PID控制器（以额定水头、额定功率下的最优PID 为参考值进行设置，即KP=6.315，KI=0.463，KD=5.551）的优越性。结果如图8所示。从图8中可以看出，自适应PID控制器比传统的定PID 控制有更短的上升时间和调节时间，这种优势在低水头工况下尤为明显。同时，自适应PID 控制器的超调量和反调量均位于工程允许的安全范围内，仅在个别工况下略高于传统方法。因此，综合来看，本文所提出的自适应PID控制器的控制性能优于传统的定PID 控制，在不同工况下均能保证最优的控制效果，且该方法易于实施，计算量小，具有重要的应用价值。

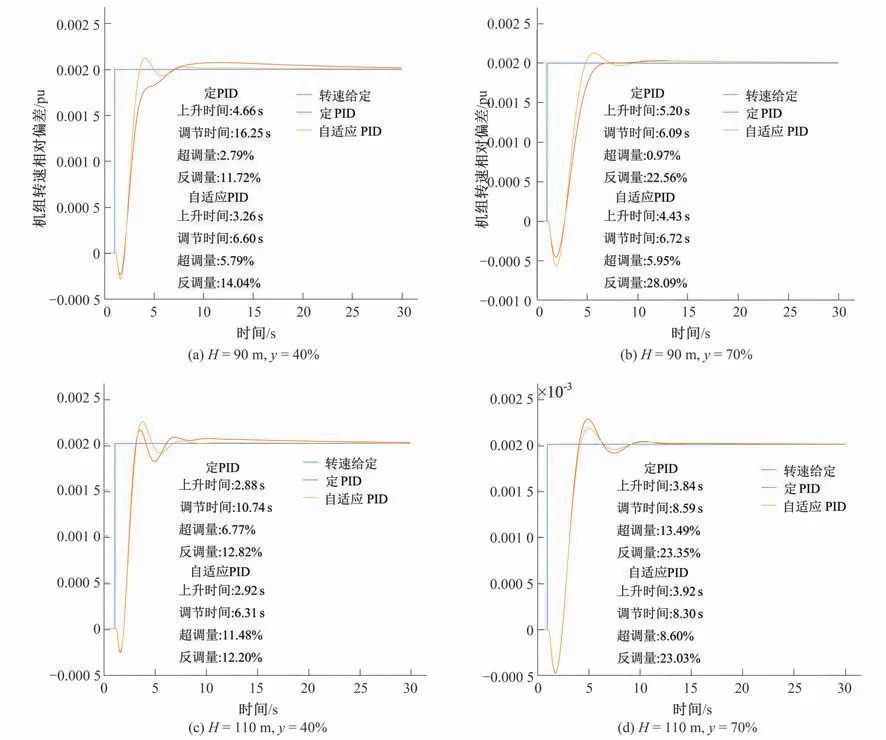
图8 水电机组不同工况下自适应控制器和定PID控制器的调节性能对比Fig.8 Comparison of regulation performance between adaptive controller and constant PID controller under different working conditions of hydropower unit

4 结 论

电网中可再生能源的高渗透率和机组运行工况的复杂多变性使得调度部门对水电机组的控制性能提出了更高要求。在此背景下，本文针对传统定PID 控制器难以适应工况变化的弊端，在保持原有控制器结构和不过多增加算法复杂性的条件下，基于神经网络和智能优化算法设计了水电机组自适应PID控制器。对比试验结果表明，所设计的控制器相较于传统控制器，能够根据机组工况变化自主调节PID控制参数，保证在任意工况下机组的调节性能均能满足达到最小ITAE 指标的要求。同时，该控制器的超调量和反调量与传统控制器相当，且均在工程要求的合理范围内，在水电机组调速器发展中具有巨大的应用潜力。