福建省私人汽车拥有量预测——基于灰色GM（1，1）模型的研究

时秀娟

（仰恩大学 数学系，福建 泉州 362014）

自1985年邓聚龙提出GM（1，1）模型（1 阶方程和1个变量的灰色模型）以来，灰色GM（1，1）模型被广大学者从不同角度进行了深入研究[1]，并已被广泛应用于经济、生产、生态及工程等领域的预测之中。

近年来，我国私有汽车的拥有量不断增加，随之而来的交通安全及环境污染等问题也不断增加。

私有汽车拥有量及其增长情况，是城市建设及交通治理的重要理论基础。本文用灰色GM（1，1）模型预测福建省私人汽车拥有量的增长情况，以期为福建省的城市建设、道路规划及交通治理等提供科学的理论依据。

一、GM（1，1）模型简介[2]

设原始数列为：

其中称为原始数据，构造数列

其中

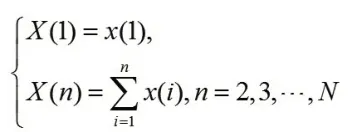
称X为累加生成数列，X（n），n=1，2…称为累加生成数据，X具有弱随机性。

GM（1，1）模型对应的微分方程为：

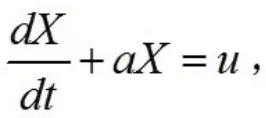
求解得

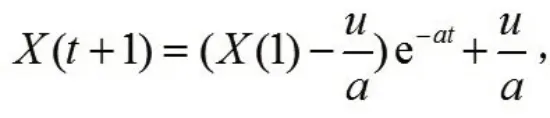
离散取值时得到累加生成数据的模型值

其中

由生成数据还原，得原始数据模型值

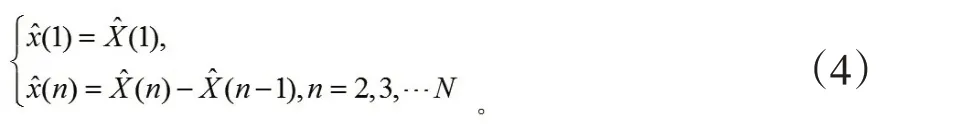
二、GM（1，1）模型在福建省私人汽车拥有量预测中的应用

利用表1中数据，可得：

表1 福建省私人汽车拥有量（单位：万辆）

将上述两矩阵代入式（2）可求得a=-0.816，u=331.2081，再由（1）式可得预测模型为：

进一步由（4）式及（5）式可得预测值表2：

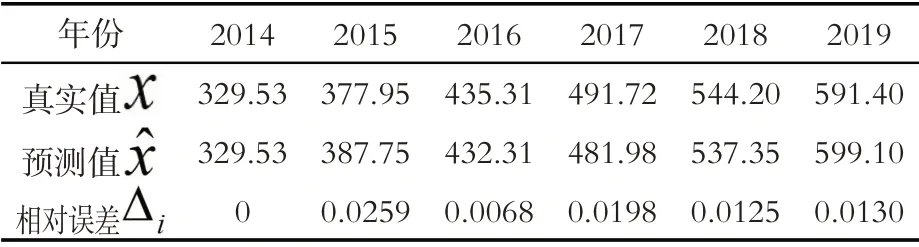
表2 福建省私人汽车拥有量预测值（单位：万辆）

三、GM（1，1）模型的精度检验

为了对模型进行检验，首先给出模型检验等级[4]：

表中符号说明：

平均相对误差：

均方差比值：

小误差概率：

根据表2可得福建省私人汽车拥有量预测值的残差和相对误差表4：

表4 福建省私人汽车拥有量预测残差和相对误差

根据表2和表4中所求数据，对模型做如下检验。

（1）平均相对误差：

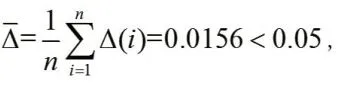
由表3可知模型的预测精度为二级。

表3 模型精度等级划分标准

（2）均方差比值C：

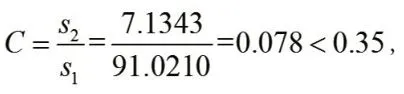
由表3可知模型的预测精度等级为一级。

（3）小误差概率P：

由表3可知模型的预测精度等级为一级。

上述三种检验模型的平均相对误差为二级；均方差为一级；小误差概率为一级。因此GM（1，1）模型为合格预测模型，通过此模型计算可得出，福建省未来5年私人汽车拥有量的预测值分别为667.93，744.67，830.20，925.63，1031.97（单位：万辆）。

结论

用灰色GM（1，1）模型计算简便、模拟结果精度较高、应用性强。通过计算，发现福建省私人汽车拥有量未来五年的增长趋势并没有减缓。