基于CMA-MESO的分级短时强降水概率预报方法研究

钟 敏，肖 安，许冠宇

（1.武汉中心气象台，湖北 武汉 430074；2.江西省气象台，江西 南昌 330096）

引言

短时强降水是指在短时间内出现的强降水事件，我国天气预报业务中一般指1 h降水量大于等于20 mm的降水事件，1 h降水量大于等于50 mm属于极端短时强降水事件［1］。短时强降水可在短时间内迅速积累形成暴洪，而暴洪是所有相关气象灾害中发生频次最高且导致伤亡人数最多的灾害［2］。短时强降水的强度主要取决于对流层低层的水汽通量辐合、水汽垂直递减率和低层大气对流有效位能（convective available potential energy，CAPE）［3］。纯粹的短时强降水天气与强冰雹、雷暴大风相比有较小的850 hPa与500 hPa温差、弱垂直风切变、较高的0℃层高度及较高的边界层露点温度等［4］。不同天气形势下不同区域短时强降水发生时，环境场物理量特征有所不同：如水汽层结大多分为整层高湿和上干下湿两类［5-7］，北方地区抬升凝结高度（lifting condensation level，LCL）普遍高于南方地区，0℃层高度普遍低于南方地区［7-10］。另外，与水汽相关的物理量对不同等级短时强降水有一定的指示作用［11-12］。

目前，利用数值模式输出参数进行强对流天气预报，可以有效提高预报水平和预报时效［13-15］，因此强对流落区预报逐步由天气型预报方法向数值模式释用和物理参数诊断方向转变［16］。在强对流天气的客观预报方法研究方面，基于常规探空数据［17］及各类数值预报模式［18-22］，统计热力、动力、不稳定等物理量数值分布特征，并通过相关性分析选取敏感因子，利用阈值法、连续概率预报等方法进行包含短时强降水在内的强对流概率预报或确定性预报。另外，利用机器学习方法对短时强降水的预报［23-25］也取得较好效果。

近年来，随着数值预报技术发展，高分辨率数值预报模式的准确率不断提高，由中国自主研发的中尺度天气数值预报模式CMA-MESO（China Meteorological Administration mesoscale model，原GRAPES区域中尺度数值预报模式），能提供0～84 h预报时效的逐小时精细化高空及地面预报产品，其风场、温度场、水汽场较全球模式在时空分辨率上有明显优势，且随着动力框架和物理过程描述的改进，该模式输出的预报场资料也有更高的准确性［26-27］。随着预报服务需求不断增长和预报内容日趋精细化，仅针对20 mm·h-1以上短时强降水的预报已不能完全满足业务需要［11］，开展不同降水等级的短时强降水预报方法研究显得十分必要，而CMA-MESO模式为该项研究提供了丰富的预报信息。因此，本文基于CMA-MESO模式，统计不同等级短时强降水样本的物理量数值分布特征，基于升、降半岭隶属函数建立短时强降水概率预报模型，并在2020年汛期中进行业务应用，为分级短时强降水预报提供技术支撑和参考依据。

1 资料

所用资料为2016—2019年6—8月中国南方9省1市（湖北、湖南、江西、安徽、江苏、福建、广西、广东、贵州和上海市）802个国家气象站、22 896个区域气象站逐时降水数据及同期CMA-MESO模式初始场数据（空间分辨率为0.1°×0.1°）。2017年7月18日以前CMA-MESO模式一天更新2次，初始场为08：00和20：00（北京时，下同）；2017年7月18日以后CMA-MESO模式升级为一天更新8次，初始场为02：00—23：00，间隔3 h。

选取雨强R≥20 mm·h-1的短时强降水，按照雨强大小分为4个等级，即20≤R＜30 mm·h-1、30≤R＜50 mm·h-1、50≤R＜80 mm·h-1及R≥80 mm·h-1，分别对应I、Ⅱ、Ⅲ、IV级。选取所有初始场时刻对应的0～1 h强降水样本及其对应的初始场物理量，按照邻近点原则进行时空匹配，建立分级短时强降水数据集。共搜集51 355站次短时强降水样本，其中I、Ⅱ、Ⅲ、IV级样本数分别为33 120、15 531、2 488、216个，不同等级雨强样本数占总样本数的百分比分别为64.49%、30.25%、4.84%、0.42%，其中III级及以上短时强降水样本占比仅为5.26%，但其属于极端短时强降水，且预报难度很大，值得做尝试性研究。

在实时预报中，所用数据为CMA-MESO模式预报场，时间分辨率为1 h，计算2020年湖北省6—8月15次短时强降水过程的不同级别短时强降水概率，并用实况降水数据进行定量检验，参与检验的站点为湖北省1662个气象观测站及其40 km范围内周边省份793个气象观测站。

文中附图涉及的地图均基于国家测绘地理信息局标准地图服务网站下载的审图号为GS（2017）3320号的标准地图制作，底图无修改。

2 物理量重要性分析

从短时强降水发生的环境条件出发，参考前人研究总结的关键物理量［28-30］，共挑选22个物理量，利用雨量数据和相应物理量形成数据集，并利用XGBoost（extreme gradient boosting）机器学习方法［31］做重要性分析。分别研究51 355个样本中17个物理量和44 093个样本中5个物理量［2017年7月18日以后CMA-MESO模式才有最有利抬升指数（best lifting index，BLI）、0℃层高度（H0）及700、850、925 hPa垂直速度（w700、w850、w925）］的重要性（图1）。可以看出，17个物理量重要性排序从高到低依次为：抬升凝结高度（LCL）、500 hPa相对湿度（RH500）、700 hPa V风分量（V700）、对流有效位能（CAPE）、850 hPa V风分量（V850）、925 hPa相对湿度（RH925）、850 hPa与500 hPa温差（ΔT850-500）、925 hPa露点温度（Td925）、850 hPa水 汽 通 量 散 度（Divq850）、850 hPa散 度（Div850）、850 hPa相对湿度（RH850）、850 hPa露点温度（Td850）、925 hPa水汽通量散度（Divq925）、925 hPa散度（Div925）、700 hPa露点温度（Td700）、K指数、700 hPa相对湿度（RH700）；5个物理量重要性排序为BLI、H0、w700、w925、w850。

3 分级短时强降水物理量统计

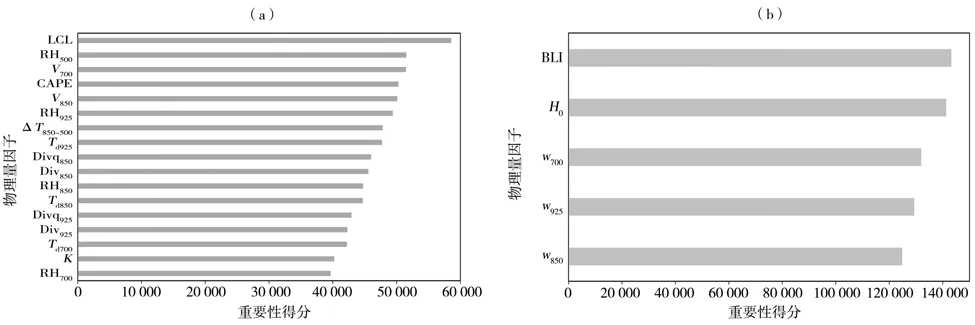
图1 17个物理量（a）和5个物理量（b）对雨强的重要性得分Fig.1 The importance score of each physical quantity to rainfall intensity for 17（a）and 5（b）physical quantities

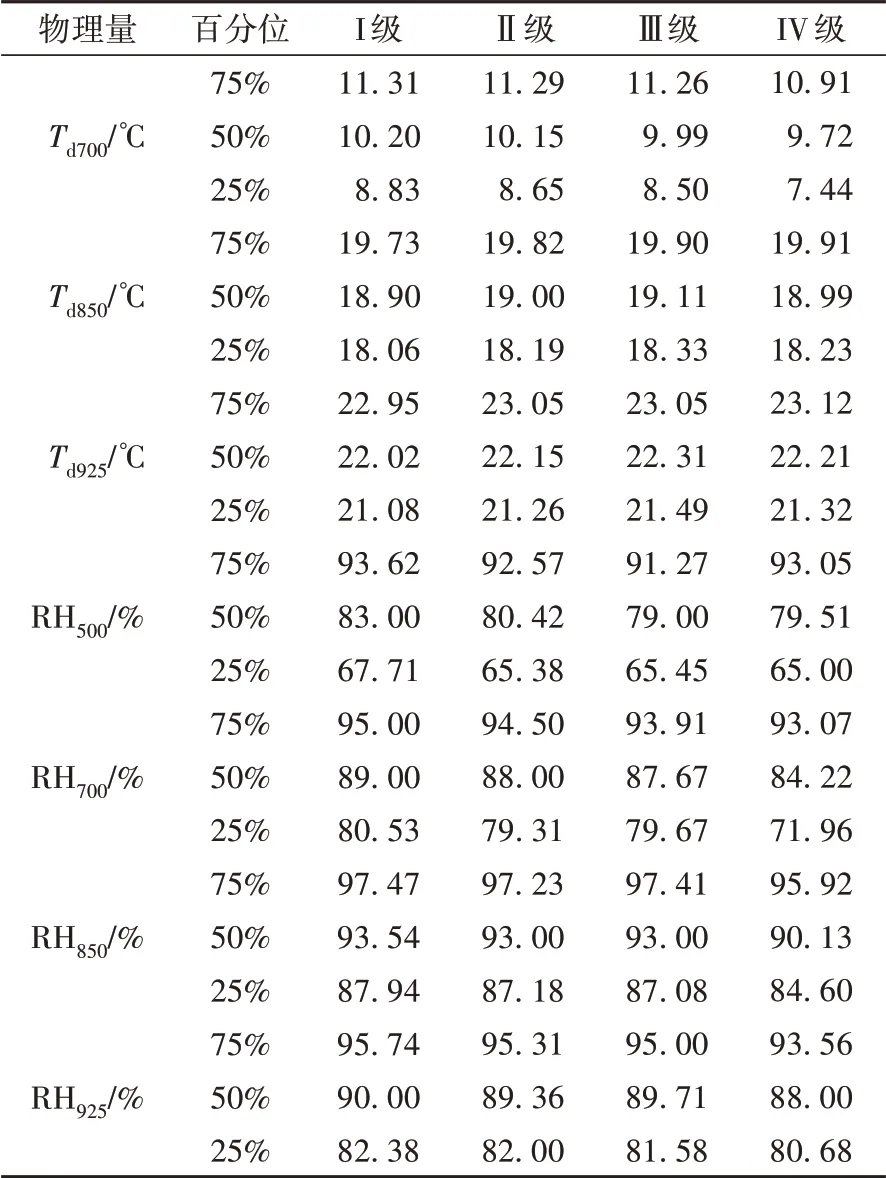
表1 不同等级短时强降水样本水汽及层结特征物理量百分位统计Tab.1 Percentile statistics of physical quantities about water vapor and stratification characteristic during short-term heavy precipitation samples with different grades

表2 不同等级短时强降水样本不稳定条件物理量百分位统计Tab.2 Percentile statistics of physical quantities about unstable condition during short-term heavy precipitation samples with different grades

统计不同等级短时强降水的物理量百分位值（75%、50%、25%分位数）分布特征（表1、表2、表3、表4），可以看到，各物理量的百分位值分布存在一定差异。由水汽及层结特征物理量统计（表1）看出，低层露点温度Td850、Td925随着雨强等级增加其百分位值略有增加，表明低层绝对水汽含量对雨强有正贡献。中层露点温度Td700却呈现出相反趋势，随着雨强等级增加其百分位值有降低趋势，这与孙继松［3］发现的对流降水过程中瞬时降水强度主要取决于水汽垂直递减率（而非整层大气可降水量）相似。即并非整层大气可降水量越大雨强就越强，雨强强的样本在水汽垂直层结上往往存在中层水汽减小特征，如IV级强降水Td700的50%、25%分位数比I级强降水分别低0.48、1.39℃。不同等级强降水的925～500 hPa相对湿度百分位值有相对一致的规律，即随着雨强等级增加，其相对湿度略有降低。从不稳定类物理量百分位值统计（表2）看出，BLI随着雨强等级增加，其百分位值呈减小趋势，即不稳定性增强；CAPE、ΔT850-500、K指数随着雨强等级增加，其百分位值基本呈增加趋势，总体上，层结越不稳定，雨强越强。从动力条件物理量百分位值统计（表3）看出，低层（850、925 hPa）散度和水汽通量散度随着雨强等级增加，其百分位值呈减小趋势，即具有更强的风场辐合和水汽辐合，这与孙继松［3］研究结论一致。V700和V850随着雨强等级增加，其百分位值基本呈减小趋势，这可能是因为引导气流不强，低空气流较弱的环境下对流单体移动缓慢，因此更易出现极端短时强降水［32］。w700随着雨强等级增加，75%、50%分位基本呈减小趋势，对应上升运动减弱；而25%分位则呈增加趋势，对应下沉运动减弱。从强降水样本总体统计结果看，上升运动强降水样本多于下沉运动强降水样本，说明CMA-MESO对大部分强降水样本能预报出上升运动，但上升速度与雨强大小对应并不好，也可能与样本数量和数值模式预报性能有关。不同等级强降水的w850和w925百分位值变化趋势不明显（表略）。暖云厚度为抬升凝结高度到融化层（大致为0℃高度）之间的厚度，是反映降水效率的重要因素［33］，降水系统的暖云层越厚，越有利于高降水效率的产生，从统计结果（表4）看，不同等级短时强降水的LCL和0℃层高度在25%、50%分位数的差异较75%分位数更明显，如各等级LCL 25%分位数为940.18～952.82 hPa，50%分位数为963.51～970.37 hPa，75%分位数为982.24～983.86 hPa。

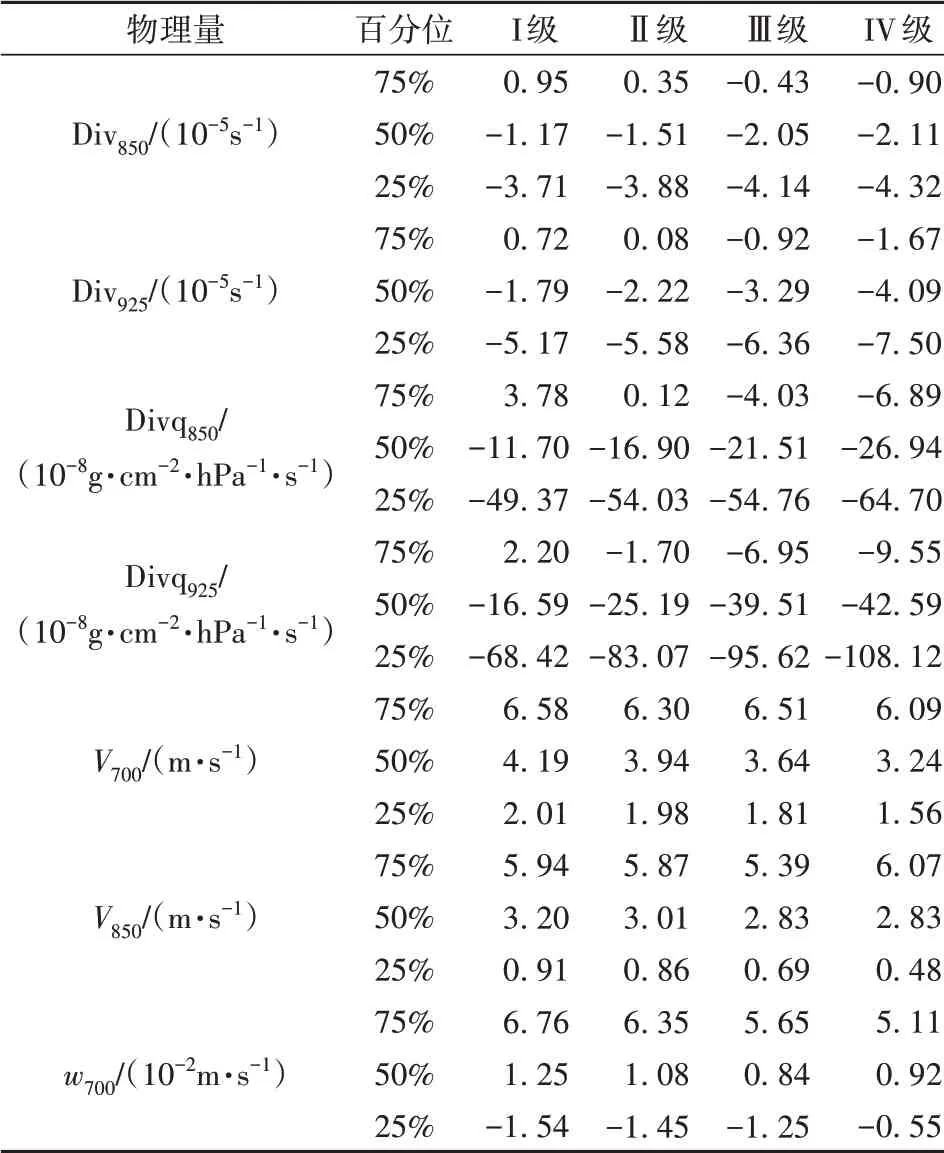
表3 不同等级短时强降水样本动力条件物理量百分位统计Tab.3 Percentile statistics of physical quantities about dynamic condition during short-term heavy precipitation samples with different grades

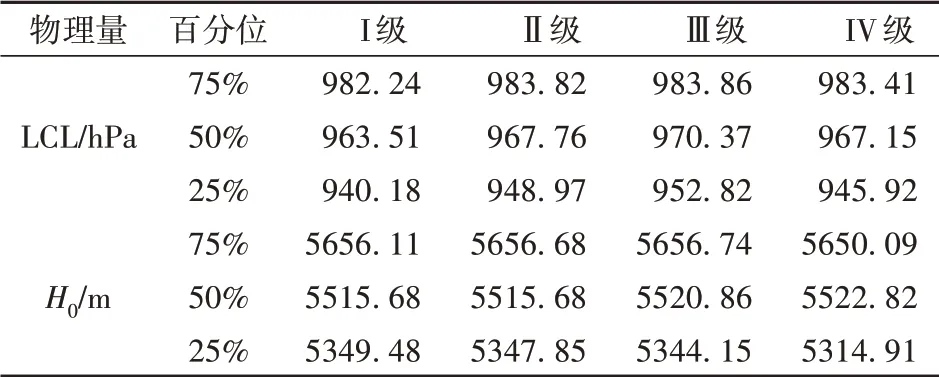
表4 不同等级短时强降水样本LCL和H0百分位统计Tab.4 Percentile statistics of physical quantities of LCL and H0 during short-term heavy precipitation samples with different grades

4 概率预报方法

从以上统计分析结果可以看出，不同等级短时强降水的环境场物理量在数值分布上并没有独立的完全区分，只是在百分位值上存在一些差异。因此建立概率预报模型时，不适宜采用传统的阈值法进行单一判断。本文采用连续概率预报方法［18］建立不同等级短时强降水概率预报模型，具体公式如下：

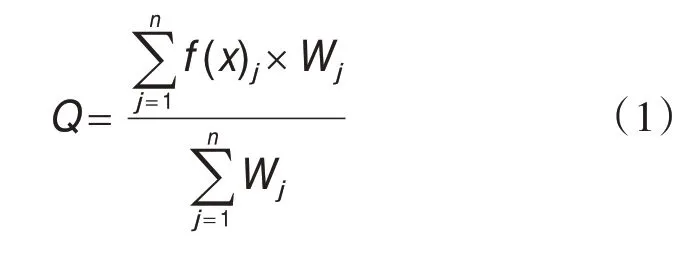
式中：Q为概率值；f（x）为隶属函数；W为权重系数；j＝1，2，3，…，n，其中n为概率预报因子数量。根据物理量重要性对22个物理量进行权重分配，其中LCL、RH500、V700、CAPE、V850、RH925、ΔT850-500、Td925、Divq850、Div850权重取1.5，其他物理量权重取1。

隶属函数f（x）的选取在预报模型中比较关键，选取方法有模糊统计法、专家经验法以及例证法等［34］，本文采用模糊统计法，通过物理量概率分布特征进行隶属函数选取。该方法优于传统的阈值法，其特征函数的取值范围从0或1扩大到［0，1］区间连续取值［35］。根据不同等级短时强降水样本相关物理量的概率密度分布特征选用不同的隶属函数，以925 hPa露点温度（Td925）和最有利抬升指数（BLI）为例（图2），其物理量值均表现为正态分布，即概率密度均呈“单峰型”，由峰值开始向两端，随着物理量值增加或减小，概率密度呈减小趋势。根据这种概率密度分布特征，分别选用升半岭和降半岭函数作为隶属函数。在建立预报模型中，BLI、散度、水汽通量散度这3类物理量选用降半岭函数，其余物理量选用升半岭函数。具体公式如下：

升半岭函数:f(x)=

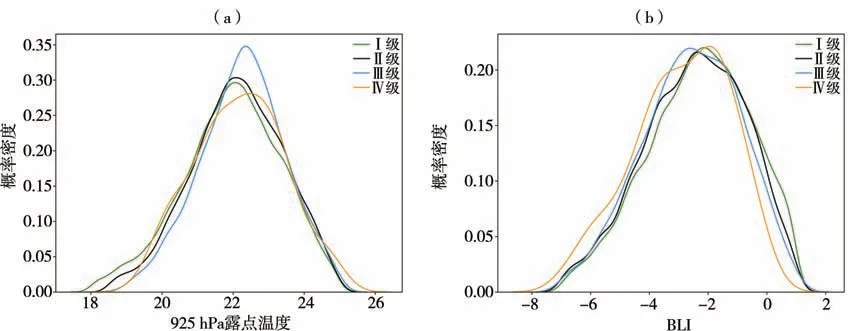
图2 不同等级短时强降水样本925 hPa露点温度（a）及BLI（b）概率密度分布Fig.2 The probability density distribution of 925 hPa dew point temperature（a）and benefit lifting index（b）during short-term heavy precipitation samples with different grades

式中：a、b为参数，分别取各物理量25%和75%分位数。

5 概率预报产品检验

对2020年6—8月15次大暴雨过程的强降水进行定量检验分析，检验对象为每日08：00和20：00起报的0～36 h预报时效的逐小时不同等级短时强降水概率预报产品，检验方法为邻域法，以40 km半径为邻域范围（标准参照全国智能预报技术方法竞赛检验方案①中国气象局预报与网络司.智能预报技术方法竞赛检验方案，2020.）。当某一级强降水概率预报产品达到或超过某概率阈值则代表该格点预报出该级别强降水。利用20 mm·h-1及以上、30 mm·h-1及 以 上、50 mm·h-1及以上、80 mm·h-1及以上强降水实况分别对I、Ⅱ、Ⅲ、IV级短时强降水概率预报产品进行检验，计算命中率（hit rate，HR）、空报率（false rate，FR）和TS评分（threat score，TS）。表5列出具体检验结果，可以看出，不同等级短时强降水的命中率随着概率阈值增加而降低，空报率随着概率阈值增加而减小。从TS评分来看，I级概率预报产品概率阈值为60%时TS评分（0.145）最好，对应命中率为55.7%；Ⅱ级概率预报产品概率阈值为65%、70%时TS评分（0.083）均最好，对应命中率分别为39.1%、24.7%，综合考虑命中率，取65%阈值最佳；Ⅲ级概率预报产品概率阈值为70%时TS评分（0.03）最好，对应命中率为21.7%；IV级概率预报产品概率阈值为80%时TS评分（0.005）最好，对应命中率为5.8%。

表5 不同等级短时强降水概率预报产品的不同概率阈值预报检验Tab.5 The forecast test of different probability thresholds of probability prediction products about short-term heavy precipitation with different grades

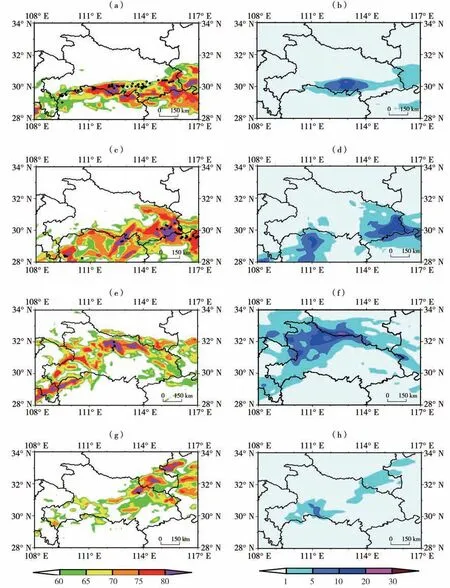
图3 2020年7月5日（a、b）、7日（c、d）及6月27日（e、f）、8月8日（g、h）08：00起报的16 h时效I级（a）、20 h时效II级（c）、10 h时效III级（e）、14 h时效IV级（g）短时强降水概率预报产品（彩色填色区，单位：%）与CMA-MESO模式预报的对应时次1 h降水量（b，d，f，h，彩色填色区，单位：mm）（左图从上到下黑色圆点分别为20 mm·h-1及以上、30 mm·h-1及以上、50 mm·h-1及以上、80 mm·h-1及以上短时强降水实况）Fig.3 The probability prediction products（color shaded areas，Unit：%）about short-term heavy precipitation with grade I for 16 h prediction time（a），with grade II for 20 h prediction time（c），with grade III for 10 h prediction time（e），with grade IV for 14 h prediction time（g）forecasted from 08：00 BST on July 5（a，b）and 7（c，d），June 27（e，f）and August 8（g，h）in 2020 and 1 h precipitation forecasted by the CMA-MESO model at corresponding time（b，d，f，h，color shaded areas，Unit：mm）（The black dots in the left figures from top to bottom are observed precipitation with rainfall intensity of 20 mm·h-1 and above，30 mm·h-1 and above，50 mm·h-1 and above，80 mm·h-1 and above，respectively）

为检验不同等级短时强降水概率预报产品的预报效果，图3为2020年4次不同等级短时强降水个例概率预报产品及CMA-MESO模式预报的对应时次1 h降水量。可以看出，7月6日00：00—01：00，湖北南部和湖南西北部出现20 mm·h-1及以上短时强降水，I级强降水概率预报产品该区域预报概率大于60%［图3（a）］，这一时次以60%为阈值，I级短时强降水的命中率为76%，空报率为47.6%，TS评分为0.45；但CMA-MESO模式预报的20 mm·h-1及以上短时强降水范围很小，出现较大范围漏报［图3（b）］。7月8日04：00—05：00，湖北东南部、湖南东北部和西北部出现30 mm·h-1及以上短时强降水，Ⅱ级强降水概率预报产品该区域预报概率大于70%［图3（c）］，这一时次以70%为阈值，Ⅱ级短时强降水的命中率为80.9%，空报率为64.9%，TS评分为0.32；但CMA-MESO模式对30 mm·h-1及以上降水全部漏报［图3（d）］。6月27日18：00—19：00，湖北西北部出现50 mm·h-1及以上短时强降水，Ⅲ级强降水概率预报产品该区域预报概率大于80%［图3（e）］，这一时次以80%为阈值，Ⅲ级短时强降水的命中率为42.1%，空报率为45.8%，TS评分为0.31；但CMA-MESO模式只预报出很小范围的20 mm·h-1及以上降水，50 mm·h-1及以上强降水全部漏报，且强降水中心与实况偏差较大［图3（f）］。8月8日22：00—23：00，湖北东北部出现80 mm·h-1以上短时强降水，IV级强降水概率预报产品该区域预报概率大于80%［图3（g）］，这一时次以80%为阈值，IV级短时强降水的命中率为36%，空报率为45.8%，TS评分为0.19；而CMA-MESO仅预报出5 mm降水量，但降水落区与强降水中心对应较好［图3（h）］。

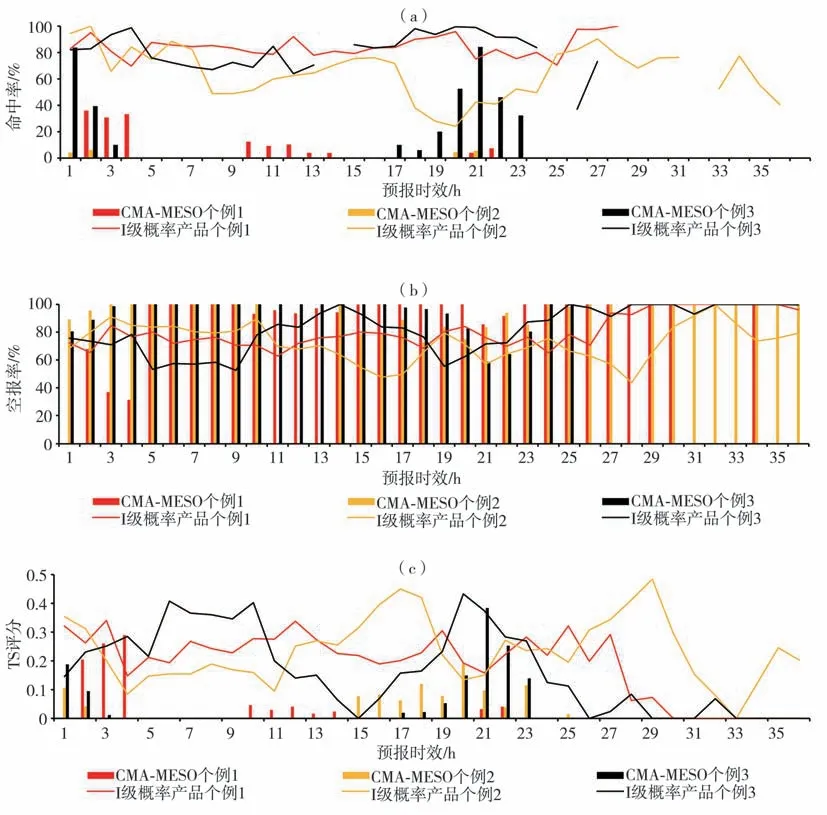
图4 I级概率预报产品20 mm·h-1及以上短时强降水与CMA-MESO模式预报的对应时次10 mm·h-1及以上短时强降水的命中率（a）、空报率（b）及TS评分（c）Fig.4 The hit rate（a），false alarm rate（b）and TS score（c）of the grade I probability product about short-term heavy precipitation with rainfall intensity of 20 mm·h-1 and above and corresponding time short-term heavy precipitation with rainfall intensity of 10 mm·h-1 and above predicted by the CMA-MESO model

为分析短时强降水天气过程不同时效的预报效果，对I级短时强降水概率预报产品与CMAMESO模式预报的3次短时强降水过程（2020年6月27—28日、7月5—6日、7月7—8日，分别简称“个例1”、“个例2”、“个例3”）做逐小时对比检验，其中I级概率预报产品以60%为20 mm·h-1及以上短时强降水的概率阈值，CMA-MESO模式由于预报雨量整体偏弱，因此以10 mm·h-1作为模式预报20 mm·h-1及以上短时强降水的阈值。从检验结果（图4）可以看到，I级概率预报产品3次个例绝大多数时次的命中率和TS评分明显高于CMA-MESO模式，且空报率明显偏低。由图4（a）看出，CMA-MESO模式3个个例的命中率均普遍较低，且超过24 h后命中率全部为0。其中个例1，I级概率预报产品各时次命中率多在80%以上，而CMA-MESO模式命中率不足40%；个例2，CMA-MESO模式的命中率仅有4个时次超过0，且最大不超过5%，而I级概率预报产品各时次命中率普遍在40%以上，最高达到100%，且第36 h预报的命中率仍然达40%；个例3，CMA-MESO模式5～16 h预报时效内命中率全部为0，而I级概率预报产品命中率为60%～80%，弥补了该时段内CMA-MESO模式的漏报情况。对空报率［图4（b）］而言，CMA-MESO模式3个个例均存在大量空报，基本以100%为主；而I级概率预报产品相对来说空报率较低，普遍为50%～90%。TS评分［图4（c）］与命中率类似，I级概率预报产品各时效TS评分普遍高于CMA-MESO模式。

6 结论与讨论

利用2016—2019年6—8月51 355个短时强降水样本，基于CMA-MESO数值预报模式建立数据集并进行统计分析，利用连续概率预报方法建立强降水概率预报模型，并在2020年汛期中进行实时业务预报及检验，得出以下主要结论：

（1）不同等级短时强降水的物理量百分位值分布存在一定差异：随着雨强增加，低层（925、850 hPa）露点温度呈增加趋势，但中层（700 hPa）露点温度却呈减小趋势；BLI、CAPE、ΔT850-500等不稳定条件物理量随雨强等级增加呈增加趋势；低层散度和水汽通量散度等动力条件物理量随雨强等级增加，风场辐合和水汽辐合越强。

（2）对2020年6—8月湖北省15次大暴雨过程0～36 h预报时效的逐小时不同等级短时强降水概率预报产品检验结果表明，将60%、65%、70%、80%分别作为I、Ⅱ、Ⅲ、IV级是否出现强降水的概率阈值，各等级命中率随概率阈值增加而降低，空报率随概率阈值增加而减小。从TS评分来看，I级概率预报产品60%阈值的TS评分（0.145）最好，对应命中率为55.7%；Ⅱ级概率预报产品65%阈值的TS评分（0.083）最好，对应命中率为39.1%；Ⅲ级概率预报产品70%阈值的TS评分（0.03）最好，对应命中率为21.7%；IV级概率预报产品80%阈值的TS评分（0.005）最好，对应命中率为5.8%。从4次不同等级短时强降水个例对比检验结果看，各级概率预报产品对CMA-MESO模式在同时次不同雨强等级强降水预报上均有较好的订正作用。

（3）通过对3次短时强降水天气过程的逐小时预报检验发现，I级概率预报产品命中率从CMAMESO模式的0～40%提高到40%～80%，预报时效也从24 h提高到36 h；概率预报产品的TS评分普遍高于CMA-MESO模式；概率预报产品的空报率在50%～90%之间，较CMA-MESO模式的空报率（大部分为100%）明显降低。

各级概率预报产品的空报率较高，尤其是50 mm·h-1及以上极端短时强降水空报率更高，这与强降水本身的中小尺度特征有极大关系，且随着雨强等级增加，极端短时强降水的样本数量急剧减小，也增加了空报的几率；此外，从强降水空间分布看出，50 mm·h-1及以上短时强降水一般空间尺度非常小，而目前中尺度数值模式的空间分辨率还不足以准确预报出这种环境场，这些都给分级短时强降水预报带来很大难度，因此今后将从强降水发生、发展的物理机制，尤其是触发机制出发，对强降水预报进行消空改进。

致谢：感谢国家气象中心为本研究提供宝贵的CMA-MESO模式资料及邓莲堂正研级高级工程师在模式性能方面提供的技术指导。