梯度压电压磁条中共线多界面裂纹的数值分析
2022-09-22周春梅
周春梅
(宁夏师范学院 数学与计算机科学学院,宁夏 固原 756000)
随着材料科学的发展,智能材料被研究者广泛关注.压电压磁材料作为一种新型的智能材料,具有特殊的磁电耦合作用,这种作用是其任何一种单一材料所不具备的. 由于其特殊的感应功能、 传导功能以及磁-电机械能的相互转换功能等,压电压磁复合材料被广泛应用于生物医疗、 军事、 航天航空、 建筑等领域.
吴桂玲[1]总结了几种智能材料的应用,文章概括了记忆合金、 智能变色材料、 压电、 压磁材料,以及它们的原理、 作用等. 田文祥等[2]研究了层状磁电复合材料界面共线裂纹平面问题,结果表明,在面内极化方向上施加面内磁势载荷时共线裂纹尖端区域的法向应力场互相干涉增强. 李纯键等[3]分析了磁电复合材料结构对磁电系数的影响,得出稳态时、 共振时磁电复合材料的磁电情况,还进一步讨论了不同层叠顺序对磁电系数的影响情况. 周勇等[4]利用有限元分析软件建立了磁电复合材料三维模型,分析了直流偏置磁场对磁电复合材料的影响,实验结果与仿真结果基本吻合. 许亮亮等[5]讨论了基于高阶剪切变形理论的磁电弹性梁的非线性静力响应,具体分析了外部荷载、 跨高比、 磁场和电场等因素对非线性静力响应的影响. 张振振等[6]提出了一种新型的低频压电-压磁复合振动俘能装置,实验结果表明复合俘能器相较于单一俘能器装置提高了俘能效率,并具有宽频俘能特性. 李飞等[7]介绍了一种铁电材料压电效应的发展进程,并讨论了铁电材料的结构、 极化状态等与压电效应之间的关系. 安明等[8]研究了异质结中铁电场效应及单项多铁性材料中电荷的磁电物理机制,为基础研究和实际应用拓宽了思路; 并指出磁电耦合效应并不局限于铁电极化装置,还可以涉及电控磁交换偏置等. 郭俊宏等[9]分析了狭长磁电弹性体中的半无限裂纹,通过数值算例给出了裂纹面受裂纹长度、 材料高度以及能量释放率的影响情况. GUO等[10]研究了反平面剪切作用下的磁电弹性纳米复合材料的三相圆柱模型,推导出具有界面效应的弹性场、 电场和磁场的封闭解. GUO等[11]对磁电弹性基体中纳米裂纹反平面问题进行了研究,研究表明,表面层与增强层的材料性能对纳米裂纹的场集中有很大的影响. 徐燕等[12]研究了压电压磁材料中正n边形孔边裂纹的反平面问题,得到了裂纹尖端强度因子和能量释放率的解析解,并给出了具体的影响规律. 谢军等[13]对梯度压电压磁圆柱轴对称的静力学响应问题进行了分析,得到了在不同边界条件下的不同参数及不同厚度下的应力、 电势和磁势的分布规律.
通过文献分析发现,研究者对复合材料中不同形状的裂纹研究很多,如孔边形裂纹,表现在模型上是在裂纹端有正多边形孔口或者椭圆形孔口等,讨论了它们的反平面问题的解析解及数值算例; 但是,对压电压磁复合材料中拼接界面多个平行裂纹的研究相对较少. 为此,本文在前期工作的基础上,基于可导通电边界条件下,对梯度压电压磁条中的多界面裂纹问题进行了分析. 采用Fourier积分变换和Gauss-Chebyshev方法求解积分方程,得到应力、 电位移和磁通量的解析表达式,通过数值求解给出应力强度因子、 电位移强度因子以及磁通量强度因子受材料参数和裂纹几何尺寸的影响情况.
1 问题描述
如图 1 所示,带宽为2h的梯度压电压磁材料(Functionally Graded Piezoelectric/Piezomagnetic Material,FGPBM)层合中含有多个裂纹间距为2c的共线界面裂纹.裂纹的长度为|bj-aj|=2a0,设第j个裂纹的左右尖端在x轴的坐标分别为aj,bj,裂纹与上下表面的距离相等.x-y平面为各向同性,即沿z轴极化,且只在裂纹表面处有切应力载荷τxy=τ(x)、 平面内的电位移Dy=D(x)及平面磁通量By=B(x).
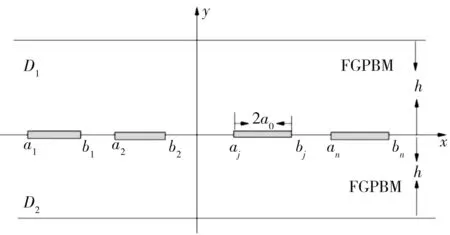
图 1 梯度压电压磁条中的共线多界面裂纹Fig.1 The collinear multi-interface cracks in gradient piezoelectric magnetic strips
压电压磁复合材料的本构方程为[14]

(2)
式中:τyz(k)为切应力;Dy(k)为平面电位移;By(k)为平面磁通量;wk为位移;φk为电势;ψk为磁势;c44为剪切模量;e15为压电系数;ε11为介电常数;q15为压磁系数;d11为磁电系数;μ11为导电率; 下标k(k=1,2) 分别对应区域D1和D2.
平衡方程为

(3)
为了方便问题的求解,设材料系数沿y轴方向按指数函数梯度分布为
[c44,e15,ε11,q15,d11,μ11]=
eβy[c440,e150,ε110,q150,d110,μ110],
(4)
式中:β为功能梯度参数;c440为剪切模量;e150为压电系数;ε110为介电常数;q150为压磁系数;d110为磁电系数;μ110为导电率.
由式(1)~式(4),可以得到材料的控制方程为

(7)
由此可得
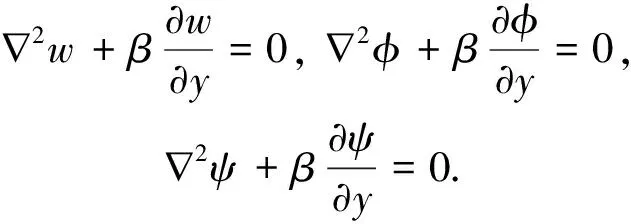
(8)
2 问题的求解
2.1 裂纹面条件
因为材料结构关于y轴对称,所以只需要考虑右边平面. 模型的边界条件[15]为
2.2 强度因子表达式
采用Fourier及其逆变换法得到位移、 电势和磁势的表达式分别为
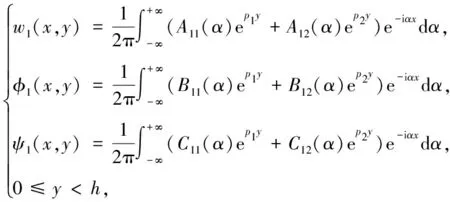
(12)
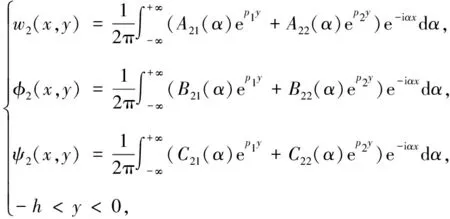
(13)
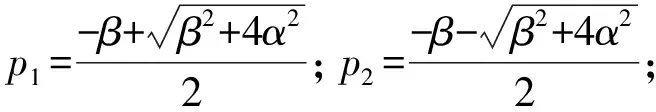
引入3个位错函数[16]s1(x),s2(x)和s3(x).
将位移、 电势和磁势的表达式代入位错函数中有式(17)成立.
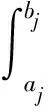
(17)
x∈[aj,bj]时,可得
A22(α)]e-iαxdα,
(18)
B22(α)]e-iαxdα,
(19)
C22(α)]e-iαxdα.
(20)
应用Fourier变换法和边界条件公式(9)~(11)解出系数Aij(s),Bij(s),Cij(s),(i=1,2;j=1,2). 再由本构方程和边界条件得到应力、 电位移和磁通量的解析表达式为

(21)

当α→∞时,k的奇异项表示为
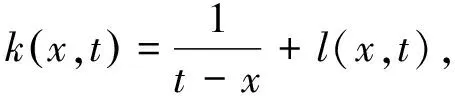
(22)
其中,
令
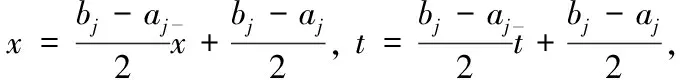
(23)
将式(22)、 式(23)代入式(21), 方程被标准化为

(26)


利用Chebyshev多项式得到裂纹端的强度因子为
式中:Fj(-1)和Fj(1)可以分别从Fj(tn-1),Fj(tn-2),Fj(tn-3)和Fj(t2),Fj(t3),Fj(t4)的二次插值得到,j=1,2,3.
由式(29)~式(34)可知裂纹左右端点的强度因子具有如下的线性关系:
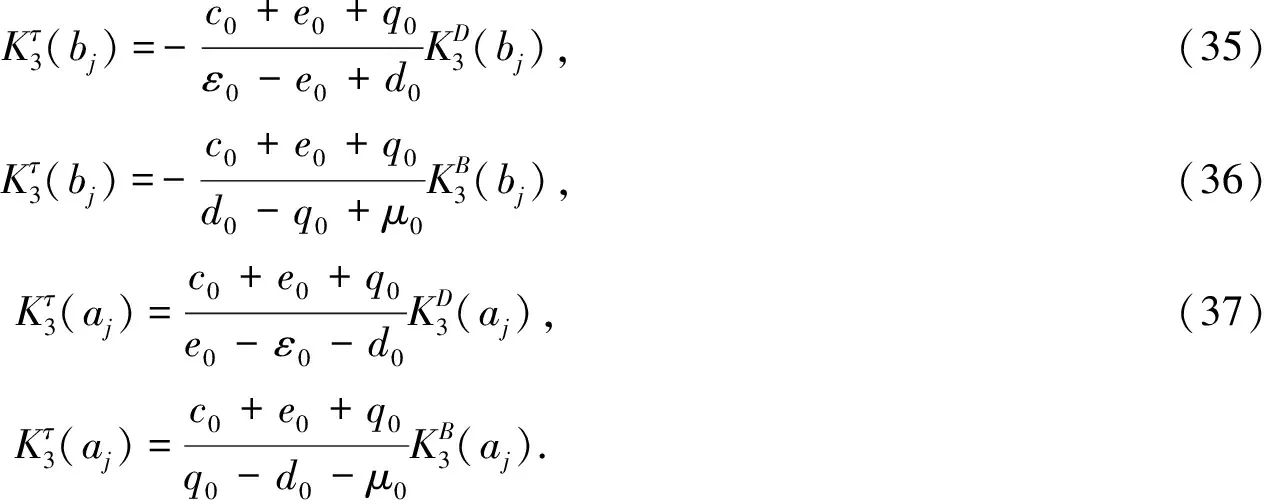
(38)
3 数值结果
以裂纹面y=0的材料BaTiO3-CoFe2O4[17]为基础,材料参数为c440=4.4×1010Pa,e150=5.8(C·m-2),ε110=56.4×10-10(C2·N-1·m-2),d110=5.2×10-12(N·s·V-1·C-1),q150=275(N·A·m)-1,μ110=297×10-6(N·s2·C-2) . 数值算例结果如图 2~图 4 所示.

图 2 不同梯度参数下强度因子K3随带宽h变化的情况Fig.2 Variations of K3 with bandwidth h under different gradient parameters
图 2 中,β取3个不同的值,总体来看,当梯度参数β逐渐增大时,裂纹端的强度因子也随之增大; 当β从0.5增大到1时,尖端的应力集中变化较小,但当β从1增大到2时,尖端的应力集中变化较大,说明梯度参数对裂纹尖端的影响较大.裂纹端的强度因子随着材料带宽h的增大而减小,最后趋近于一个定值,这与文献[9]的结果一致.

图 3 不同带宽下强度因子K3随裂纹长度a0变化的情况Fig.3 Variations of K3 with crack length a0 under different bandwidths
图 3 中,材料带宽h取3个不同的值,在h值不变的情况下,裂纹长度a0逐渐增大时,裂纹端强度因子也随之增大; 当a0值不变时,裂纹端强度因子随着带宽h的增大而减小; 随着h的逐渐增大,尖端的应力集中变化趋势几乎一样,这说明带宽h对应力集中的影响会越来越弱.

图 4 不同梯度参数下强度因子K3随裂纹长度a0变化的情况Fig.4 Variations of K3with crack length a0 under different gradient parameters
由图 4 可知,尖端的强度因子随着梯度参数β和裂纹长度a0的逐渐增大而增大.当β取0.5时,裂纹左右端应力集中变化非常明显,但当β取1和2时,应力集中变化较小且趋于平缓,最后趋近于一个定值.
4 结 论
本文分析了梯度压电压磁条中的共线多界面裂纹问题. 文中给出电渗透型边界条件,采用Fourier及其逆变换技术对问题进行转化,给出对应的奇异积分方程,通过积分方程的求解,得到位移、 电势和磁势的表达式及强度因子的表达式. 最后,通过数值算例分析了梯度参数、 裂纹长度和材料带宽对强度因子的影响. 裂纹左端的强度因子比裂纹右端的强度因子大. 由数值算例得到,梯度参数增大,裂纹端的强度因子随之也增大,并且随着梯度参数变化幅度的增大会有更明显的增大趋势. 对于同一梯度参数值,随着裂纹长度的增大逐渐增大; 随着材料带宽的增大逐渐减小,并且随着带宽变化幅度的增大,应力集中的变化趋势越来越小,说明材料越宽越安全. 本文研究为工程中的材料拼接提供了理论参考依据.
