对高中数学新教材一道三角恒等变换习题的拓广探索
2022-09-22张静元
张静元
(云南省昆明市教育科学研究院 650000)
1 问题呈现
题目(人民教育出版社《普通高中教科书数学必修第一册A版》第230页,简单的三角恒等变换习题5.5拓广探索第18题)观察以下各等式
分析上述各式的共同特点,写出能反映一般规律的等式,并对等式的正确性作出证明.
2 问题解决方法
2.1 从角的特征探索发现共同规律
综合考查三个等式中的角发现共同规律:
60°=30°+30°;45°=30°+15°;50°=30°+20°.
以第三个等式为例证明:

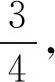
2.2 写出反映一般规律的等式
三个等式中给出的两个角60°,30°;45°,15°;50°,20°都满足β=30°+α,则一般规律的等式为:
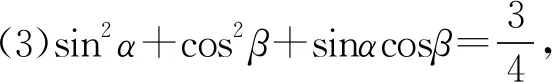
2.3 从不同的角度证明等式的正确性
思路1 和差角公式.
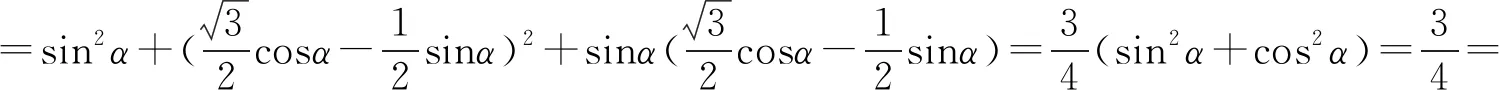
思路2 降幂扩角公式.
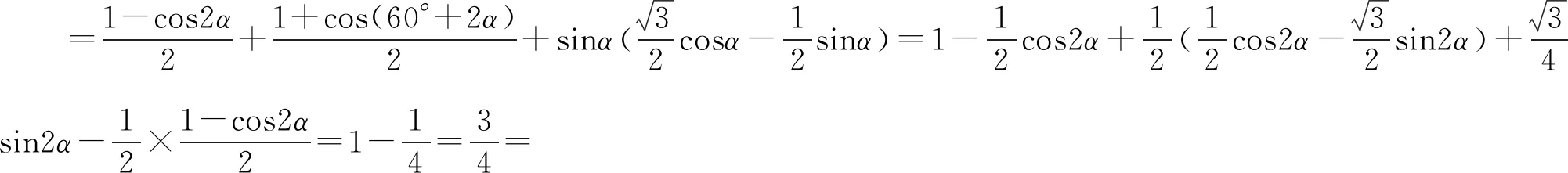
思路3 三角函数在单位圆上的定义.
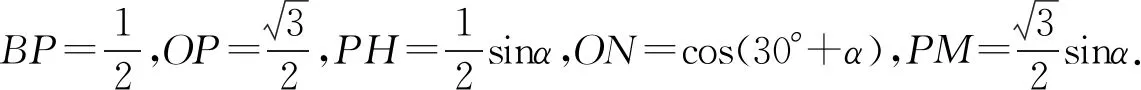
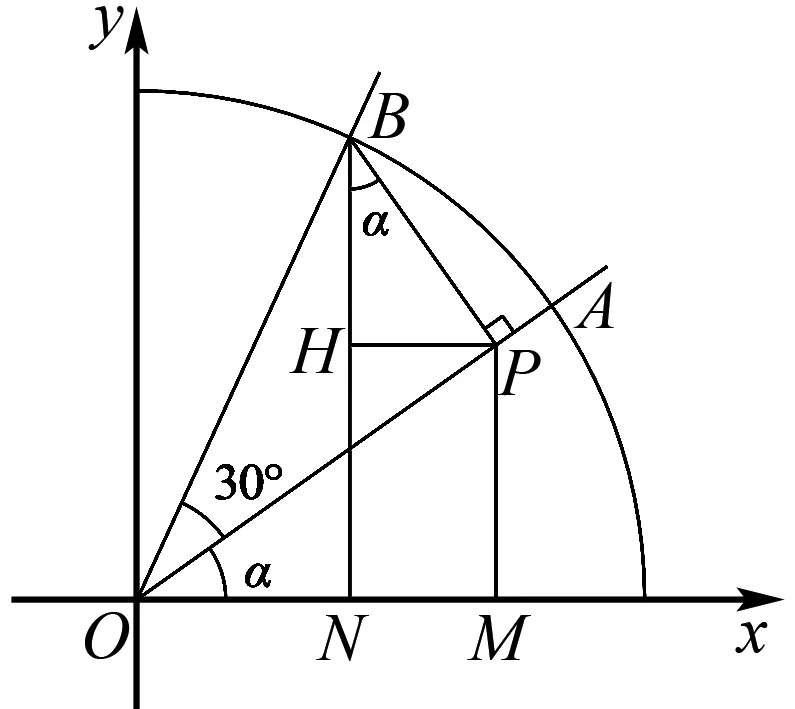
图1
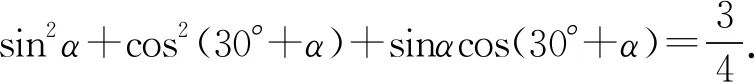
思路4解直角三角形.

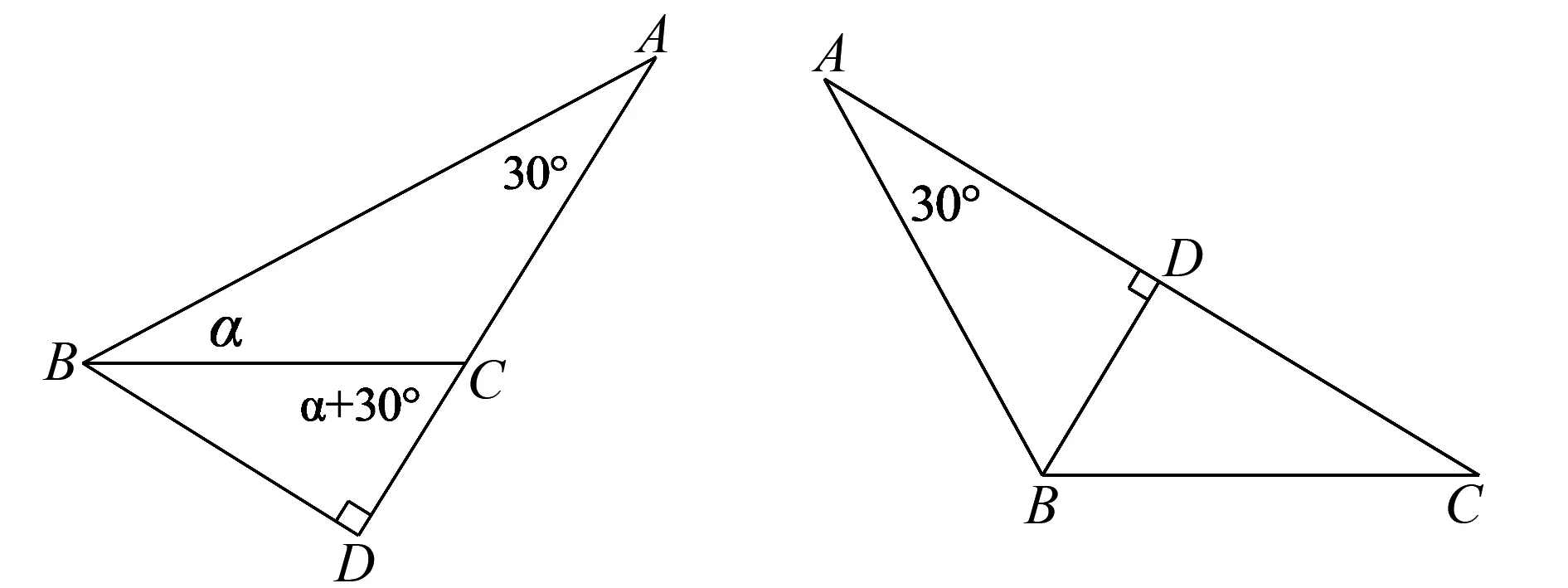
图2 图3
当α为钝角时,如图3,同理可证.同理,当α为特殊角或大于180°,等式成立.
思路5解三角形.
在△ABC中,A=α,B=30°,则C=150°-α.设b=1,由正弦定理,得a=2sinα,c=2sin(150°-α).
由余弦定理,得c2=a2+b2-2abcosC,则4sin2(150°-α)=4sin2α+1-4sinαcos(150°-α).
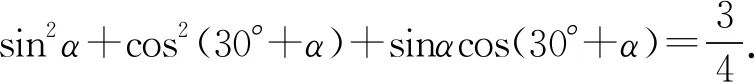
3 问题探索
3.1 统一函数名

思考1 对于等式中的60°,能改为任意角吗?
猜想:对任意的角β,sin2α+sin2(β-α)+sinαsin(β-α)=sin2β.下面取特值验证:
当β=90°,等式左边=sin2α+cos2α+sinαcosα=1+sinαcosα,等式右边=1,显然对任意角α等式不正确.所以,对于任意的角β,sin2α+sin2(β-α)+sinαsin(β-α)≠sin2β.
既然对任意角β等式不成立,那么角β能取到哪些值才能使等式成立?
思考2 探索角β取何值能使猜想正确.
把β作为自变量,构造函数f(x)=sin2α+sin2(x-α)+sinαsin(x-α)-sin2x,其中α为参数,用计算机作出函数f(x)的图象,考查函数f(x)的零点,即为等式成立的情况:
如图4,函数f(x)部分零点从左至右依次为:
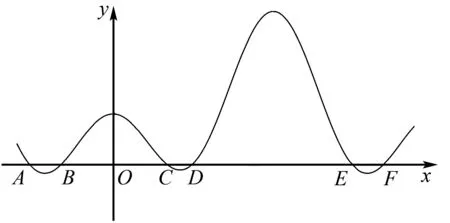
图4


图5
3.2 探索角的特征
由于sin260°=sin2120°,等式写成sin2α+sin2(60°-α)+sinαsin(60°-α)=sin2120°,发现α+(60°-α)+120°=180°,如果规定这三个角在(0°,180°)内,联想这三个角为△ABC的内角,猜想sin2A+sin2B+sinAsinB=sin2C,其中A+B+C=180°.由于上面的探索,等式不能对任意的角C都成立,下面探索在△ABC中,满足什么条件,等式sin2A+sin2B+sinAsinB=sin2C能成立.
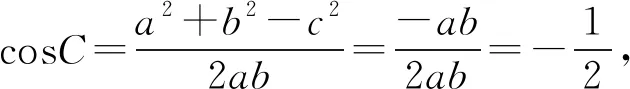
3.3 拓广问题
通过探索发现,在三角形中,由余弦定理a2+b2-2abcosC=c2变形公式可得:sin2A+sin2B-2sinAsinBcosC=sin2C.教科书中的三个等式,就是余弦定理变形公式中C=120°,A+B=60°的情形.归纳为:sin2A+sin2B-2sinAsinBcos120°=sin2120°,其中A+B=60°.
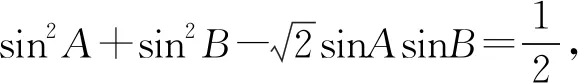
通过以上的探索,追溯等式成立的源头,这一类等式是余弦定理在一定条件下的情况,通过统一函数名,发现三个角恰好为一个三角形的三个内角,借助正、余弦定理得到一般情况都能成立的条件.将问题拓广,对锻炼学生思维,培养探究意识,学会用不同路径去探索数学问题,有较好的示范性.
